山区土壤重金属空间插值性能的改进

张榆霞， 李宝磊, 施 择，万国盛

1.云南省环境监测中心站， 云南 昆明 650034 2.云南大学信息学院， 云南 昆明 650091

土壤重金属污染给世界各地带来严重的环境和健康问题[1]。土壤中重金属的空间分布图被广泛应用于识别污染源、预测污染趋势以及控制潜在的污染风险。山区水域、悬崖和山谷等自然条件给土壤均匀采样带来了巨大的困难。根据客观实际条件，利用有限采样点的样品测试数据，获得精准的土壤重金属空间分布图，对于进一步进行空间评价、分析和预防环境污染非常有意义。为此，探索采样稀疏、采样点分布不规则的情况下，如何获得精确稳定的插值结果显得至关重要。

目前广泛应用于土壤性质空间插值的方法主要有反距离(IDW)[2]、普通克里格(OK)[3]和径向基函数神经网络(RBFANNs)[4]插值法。基于几何学意义的IDW插值方法忽略了土壤重金属含量高度复杂的非线性特征而导致精度不高。 基于统计学意义的OK插值法虽然得到了广泛的应用,但其应用的假设条件和采样要求[5]，使其不能很好地描述具有非线性系统特征的土壤性质空间分布。近年来，许多学者将人工神经网络较强的非线性映射能力应用于土壤性质的空间分布研究中[6],并取得了较理想的结果，但由于人工神经网络的学习过程具有随机性,会降低其插值结果的稳定性。为此,研究引入了一种集成径向基函数神经网络(IRBFANNs)模型，用以提高山区土壤重金属浓度插值的精确性和稳定性。基于云南省楚雄市南部山区表层土壤中重金属锰和钒的样品测试数据，进行了3种不同等级采样密度下的IDW、OK、RBFANNs和IRBFANNs插值法比较实验研究。

1 实验部分

1.1 IRBFANNs空间插值模型

集成技术的基本思想是通过训练多个神经网络，并将其预测结果进行平均以期消除误差，提供更精确、稳定的预测[4]。IRBFANNs预测需要2个步骤：首先在使用该模型之前用Bagging[7]方法对总训练数据重复取样获得不同的子训练数据集，用以训练各个RBFANNs模型，并通过式(1)计算各个模型的权重；然后把预测点信息Xin(被预测点的经度、纬度、临近5个采样点采样值组成的输入向量)输入到各个RBFANNs模型，通过式(2)计算IRBFANNs模型的输出。

(1)

(2)

1.2 实验数据

以云南省楚雄市南部以及周边地区为试验区。该区域系云贵高原中部，红河水系与金沙江水系分水岭地带，地跨100°59′E～101°52′E，24°1′N～25°3′N，面积达9 938.641 5 km2，山地是该区域主要的地貌。地势西北高、东南低，海拔为556～3 657 m，海拔落差达3 101 m。土壤主要为紫色土、水稻土、红壤和黄棕壤。该区域河沟纵横、山地海拔落差大的特点给采样点布设带来较大难度。以该区域内42个采样点的土壤重金属锰和钒检测值为研究数据。在实验之前，所有数据都做了归一化处理，其分布满足标准正态分布。

1.3 实验设计

为了比较IDW、OK、RBFANNs和IRBFANNs插值法插值的精确性和稳定性及其受采样密度的影响情况，基于42个采样点数据进行了A、B、C 3项实验，分别随机选取41、26和16个测试样本子集，以保证研究结果的广泛适用性。每项实验中都进行了100次独立的随机测试，每次测试中都记录预测误差的均方值(RMSE)用于统计分析。IDW插值法通过预测点周围10个采样点的欧氏距离以及采样值进行预测；OK插值法通过使用Matlab工具箱中的dace函数实现，回归模型和相关函数分别为Regpoly2和Corrgauss, 相关函数的初始参数theta是10；RBFANNs通过使用Matlab工具箱中的newrb函数实现，其中采用“试错法”确定的锰和钒的最优散布常数分别为0.3和0.05，其他参数使用工具箱提供的默认参数；在IRBFANNs中，每个子训练集都是通过使用Bagging算法从总训练数据中随机重复抽取80%数据生成。

插值性能的评价指标RMSE如式(3)所示：

(3)

式中，n为检验数据集中的检验数据的个数，z*(xi)为插值方法对采样点xi处土壤重金属含量的预测值，z(xi)为采样点xi处采样获得的土壤重金属含量的真实值。RMSE值越小则预测误差就越小，插值精度就越高；RMSE值的波动范围越小，则插值算法的稳定性就越高。

2 结果与讨论

2.1 精确度与稳定性统计分析

图1展示了100个测试实验中得到的RMSE统计量。

图1 RMSE箱图图例

由图1可见，该箱图描述了统计数据的中值、上五分位值、下五分位值、最大值以及最小值。中值越小则算法的插值精度就越高，上、下五分位值的差越小，则误差波动范围就越集中，算法的稳定性就越强。

4种方法在3种采样密度下对土壤中锰和钒元素总量的预测实验结果如图2和图3所示。

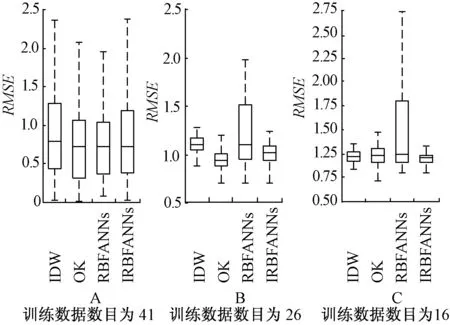
图2 锰RMSE箱图

图3 钒RMSE箱图

2.1.1 采样密度对插值性能的影响

由图2和图3可见：①4种方法中，RMSE指标的中值都随着训练数据的减少而增加，说明4种方法的精确度随着采样密度的降低而降低，并且RMSE指标的上下五分之一分位值之间的差值随着训练数据的减少而减少，这是由于训练数据减少时模型的精确度下降，预测误差都偏大，导致RMSE值的范围减小。②各类方法性能下降的程度不一致。相比较而言，IDW和OK方法的RMSE中值随着训练数据的减少具有较明显的增加，这说明IDW和OK方法的精确度易受采样密度的影响。RBFANNs方法的RMSE中值的增加幅度没有IDW和OK方法明显，但是其上下五分之一分位值之间的差值远远大于其他方法，说明受采样密度降低的影响，RBFANNs方法的精确度虽然下降得不是那么明显，但是稳定性有明显的下降。③在所有方法中，随着采样密度的降低，IRBFANNs方法的RMSE中值上升幅度最小，上下五分之一分位值之间的差值变化不大，说明IRBFANNs精确度受采样密度的影响较小且能保证插值的稳定性。

总之，虽然随着训练数据的减少，所有方法的预测性能都有所下降，但IRBFANNs的RMSE中值增加最少，特别在训练数据数目为16时，IRBFANNs的RMSE中值以及上下五分之一分位值之间的差值都是最小的，这表明IRBFANNs方法应用在采样点密度稀疏的情况时，精确度和稳定性优于其他方法。

2.1.2 不同方法插值性能比较

观察图2和图3，同一个项目，不同方法之间的实验结果表明：

1)训练数据数目最多(项目A，41点)时，同一种元素各个方法的RMSE中值和上下五分之一分位值之间的差值差异不大，表明训练数据数目最多时，各个方法的差异不是很明显。而OK方法获得最小的RMSE中值，其他方法获得的RMSE中值略大于OK方法，这说明采样密集时，基于地理统计学的OK方法表现出众。由图3可见，在钒的实验中，IRBFANNs方法的RMSE中值以及上下五分之一分位值之间的差值明显小于RBFANNs方法，这说明集成有助于提高基于神经网络方法的插值精度和稳定性。

2)当训练数据数目为26点时，各个方法获得的中值以及上下五分之一分位值差值差异相对于项目A趋于明显。传统的IDW和OK方法，RMSE中值以及上下五分之一分位值差值最小。而基于RBFANNs方法获得的中值以及上下五分之一分位值之间的差值都较大，这说明传统神经网络方法的精确度、稳定性不如其他传统方法。

3)当训练样本减少到16点时，传统的IDW和OK方法获得的中值以及上下五分之一分位值之间的差值均比RBFANNs方法小，但比IRBFANNs方法大。这说明采样密度稀疏时，集成神经网络方法的精确度和稳定性优于其他方法。IRBFANNs方法在RMSE中值以及上下五分之一分位值之间的差值都明显小于RBFANNs方法，这一结论与项目A、B一致。这进一步说明集成有助于提高基于神经网络方法的插值精确度和稳定性。所有方法中，IREBANNs方法获得最小的RMSE中值以及上下五分之一分位值之间的差值，这表明IRBFANNs方法应用在采样点密度稀疏的情况时具有较好的插值精确度和稳定性。

总之，样本点最多时，各种方法的插值精确度和稳定性差异不大，传统OK和IDW方法略优于其他方法。样本点适中时，各个方法的插值精确度和稳定性差异趋于明显，各个方法对于不同的元素表现不一致。样本点最少时，各个方法的插值精确度和稳定性差异明显，IRBFANNs优于其他方法，其插值精确度和稳定性都最好。

综上所述，训练数据减少时，所有模型的预测精确度和稳定性都有不同程度下降，并且各种方法对于不同的元素下降程度不同；对于所有元素样本点最少时，尽管各种方法的性能都有明显的下降，但是IRBFANNs方法插值精确度和稳定性都优于其他方法。

2.2 空间插值可视化分析

为了更直观地观察各个方法的插值效果，图4显示了锰元素基于4种方法，在不同采样密度条件下的插值结果空间分布。

2.2.1 采样密度对插值效果的影响

由图4可见，同一个方法，随着采样点的减少，各个方法获得的空间分布图的分辨率降低，其所描述的空间分布情况变得模糊。但是各个方法性能降低的程度有所不同。相比较而言，随着采样密度的降低，传统的IDW和OK方法获得的插值空间分布图的分辨率、细节描述性有明显的下降。基于神经网络的RBFANNs和IRBFANNs方法，获得的空间插值分布图所描述的空间分布情况和质量，受采样点减少的影响较小，细节保留较为完整。

2.2.2 不同方法插值效果比较

由图4可见，样本点最多时，IDW方法虽然提供了一个确定的锰元素含量插值表面，但是插值空间分布图粗糙，所描述的空间分布情况缺乏空间连续性，这可能是由于样本点较集中区域中，离插值点极近的样本点对该插值点的估计值影响特别大，而孤立样本点对各个方向插值点的作用是稳定的逐渐衰弱的。

OK方法获得的插值空间分布图多斑点，颜色差异性较小，其描述的空间分布情况平滑，缺乏细节信息，可见OK方法受样本点非均匀分布的影响容易产生孤岛效应，其插值的结果缺乏合理性。

与OK方法相比，RBFANNs方法获得的插值空间分布图描述了更多的空间差异性，并且从图中还可以看出该元素的空间分布趋势，这在OK方法获得的插值空间分布图中是很难观察出来的。RBFANNs方法较IDW和OK方法，在锰元素空间差异细节性描述以及空间分布趋势方面又有一定程度的提高，但是该方法获得的插值数据的范围与样本数据范围(标准正态分布)不一致，插值数据最大值和最小值远远高于或者低于样本数据的最大值和最小值，这是由于RBFANNs的插值表面极易受边缘效应的影响，研究区域的边缘插值结果往往偏大或者偏小，造成插值结果不稳定。

IRBFANNs方法获得的插值空间分布图不仅平滑并具有较好的连续性，极少有斑点，空间变异明显，且插值数据范围与样本数据范围相一致，可见其能够合理详细地描述元素空间分布的局部细节以及分布趋势。同样的采样密度下，样本点适中和样本点最少时，通过观察所有元素的插值空间分布图，可以得出与样本点最多时相一致的结论。

综上所述，IRBFANNs插值方法能够有效合理地描述土壤重金属空间分布的空间变异性的细节和空间分布趋势。与其他插值方法相比，IRBFANNs在样本点较少的情况下能够获得质量相对较好的土壤重金属空间分布图。这与“2.1节”中的统计分析结论相一致。

3 结论

使用IRBFANNs插值方法，可以提高土壤重金属含量空间插值的性能。通过误差统计和插值可视化分析，与传统插值方法相比较，该方法在采样密度稀疏的情况下，产生预测误差的均值、中值以及上下五分位值都最小，表明在样本点数量减少时，IRBFANNs算法能够获得最好的插值精确度和稳定性，据此获得了更准确的区域重金属分布及趋势图，从而提高山区土壤重金属分布预测性能。

[1] Alloway B J, Ayres D C. Chemical principles of environmental pollution[M]. Florida: CRC Press, 1997.

[2] Tomczak M. Spatial interpolation and its uncertainty using automated anisotropic inverse distance weighting (IDW) cross validation /jackknife approach[J]. Journal of Geographic Information and Decision Analysis,1998,2(2):18-30.

[3] Oliver M A, Webster R. Kriging: a method of interpolation for geographical information systems[J]. International Journal of Geographical Information System,1990,4(3):313-332.

[4] 刘思聪.B/S 结构的云南省土壤重金属空间插值分析系统[D].昆明：云南大学,2012.

[5] 王政权.地统计学及在生态学中的应用[M]. 北京：科学出版社,1999.

[6] 何勇,张淑娟,方慧.基于人工神经网络的田间信息插值方法研究[J].农业工程学报,2004,20(3):120-123.

[7] Breiman L. Bagging predictors[J]. Machine learning,1996,24(2):123-140.