结构突变条件下农产品期货市场波动率的预测*

杨 科，田凤平

(1．华南农业大学经济管理学院，广东 广州 510642；2．中山大学国际商学院，广东 广州 510275)

农产品期货市场的健康发展，对解决我国的“三农”问题，特别是稳定粮食安全生产，有着重要的作用和意义。但农产品期货是一柄“双刃剑”，在发挥其市场功能的同时仍难以摆脱衍生品固有的高风险特性。由于农产品期货市场采用的是保证金交易、逐日盯市以及强行平仓制度等，其价格的波动会造成投资者获利和损失成倍放大，市场风险远高于现货交易，使用不当易诱发金融市场的极端风险。因此，准确度量和预测农产品期货市场波动率对于投资者有效规避投资风险以及管理层科学合理发挥农产品期货的市场功能，最终促进金融市场平稳较快发展具有重要的理论价值和现实意义。

国内对农产品期货市场的研究大致可以分为理论研究和实证研究两个方面。理论研究主要侧重于从制度出发，研究合约制定、交割方式等内容，着眼于如何建设我国农产品期货市场等方面。实证研究主要侧重于借鉴西方金融工程理论，对我国农产品期货市场的有效性、市场功能等方面进行数量分析，例如，王辉等[1]基于修正ADCC模型和DADCC模型研究了我国农产品期货套期保值中基差和“消息”的非对称效应及其对套期保值效果的影响。国内学者对我国农产品期货市场波动率的研究文献非常少，并且绝大部分都是采用基于低频收益率数据的GARCH族模型来研究我国农产品期货市场波动率的特征。例如，王金媛[2]基于GARCH族模型发现我国农产品期货市场波动率具有长记忆性和不对称性；魏宇[3]基于能够刻画非对称杠杆效应的EGARCH、GJR和APARCH等非线性GARCH模型发现我国商品期货市场的波动率的非对称杠杆效应不明显；刘向丽等[4]通过构建ACD-GARCH-M模型研究了我国期货市场价格的波动特征，发现久期、交易量等微观结构变量能很好的吸收波动率的聚集性。然而，国内尚未出现对我国农产品期货市场波动率预测的研究，尤其是基于高频数据的已实现波动率预测方面。因此，本文将探讨我国农产品期货市场已实现波动率的预测问题。

在已实现波动率的预测建模方面，最具代表性的是Andersen等[5]的lnRV-ARFIMA模型和Corsi[6]的HAR模型。最近，国外学者对ARFIMA模型和HAR模型进行了重要地扩展和改进：Giot 等[7]将ARFIMA模型扩展为考虑波动率的不对称性的ARFIMAX模型，进一步提高了ARFIMA模型对已实现波动率的样本外预测精度；Corsi等[8]将负收益率作为解释变量加入到HAR模型中，构建的具有不对称性的AHAR模型；Beltratti等[9]、Degiannakis[10]和Corsi等[11]等分别通过FIGARCH模型、TARCH模型和GARCH模型来刻画ARFIMA模型和HAR模型的误差项的条件异方差性，构建的ARFIMA-FIGARCH模型、ARFIMA-TARCH模型和HAR-GARCH模型也进一步提高了ARFIMA模型和HAR模型的样本外预测精度；为了进一步考虑周内效应对已实现波动率预测的影响，Martens等[12]构建的ARFIMA-DARL模型进一步提高了ARFIMA模型样本外预测性能。国内学者王春峰等[13]构建的长记忆随机波动率模型、魏宇[14]构建的基于多分形波动率(Multifractal volatility)的ARFIMA模型以及杨科等[15]构建的半参数预测模型也进一步提高了波动率的样本外预测精度。

然而，上述文献都假设ARFIMA过程或HAR过程是稳定不变的，并且都采用不断扩展的或固定的估计窗口大小来估计已实现波动率预测模型，以获得已实现波动率的样本外预测值，均没有考虑结构突变对波动率预测的影响。但金融市场周期性的会受到重要的突发金融事件的影响，如1987年的股市崩盘、1997年的亚洲金融金融危机以及最近的次贷危机引发的全球金融危机。这些突发的重要金融事件可能会导致金融市场波动的大幅变动，因此，波动率模型的参数需要进行相关的结构突变调整。鉴于此，本文首先检验农产品期货市场已实现波动率序列的结构突变特征；然后以ARFIMAX-FIGARCH模型为基础来分析结构突变对模型参数估计的影响；接着，为了适应农产品期货市场已实现波动率的结构突变特征，构造基于不同估计窗口大小的ARFIMAX -FIGARCH模型及其线性组合预测模型和非线性组合预测模型来预测农产品期货市场的已实现波动率；最后，采用基于自助法的MCS检验不同损失函数评价标准下，评价和比较了各类单项预测模型和组合预测模型对农产品期货市场波动率的预测性能。

1 模型与方法

1.1 波动率的高频估计

按照Andersen等[16]的定义，已实现波动率(Realized Volatility，RV)为日内高频收益率的平方和，可作为每日波动率的代理变量。假设Pi,t表示农产品期货在交易日t的第i个价格观测值，则交易日t的第i个日内高频收益率为ri,t=100×(logPi,t-logPi-1,t)。假定交易日t可以获得的高频收益率数目为M，则交易日t的已实现波动可以表述为

(1)

上述估计方法在一定的条件下是真实积分波动率的无偏估计量，无需复杂的参数估计，并且较好地解决了ARCH模型和随机波动率模型中的维数灾难问题。但由于期货市场不是24小时连续交易，能观察到和记录的高频交易数据只能反映有交易时段的市场波动状况，而无法包含无交易时段的市场波动信息，因此，式(1)所述的已实现波动率估计量是市场真实波动率的有偏估计量。为考虑农产品期货市场休市期间的波动状况，本文采用Martens[17]的尺度参数δ(具体参见文献[17])对式(1)所述的估计量进行偏差修正，修正后的已实现波动率估计量可以表述为

(2)

1.2 结构突变的检验

参照Choi等[18]的研究，本文采用Bai等[19-20]的纯均值多突变模型来考察农产品期货市场波动率序列的结构突变特征。N-均值突变模型表述如下

lnRVt=mj+εt,t=Tj-1+1,Tj-1+2,…,Tj

(3)

其中，j=1,2,…,N+1，mj为lnRVt的均值。结构突变点(T1,T2,…,TN)未知。扰动项εt可能存在序列相关和异方差。本文采用检验统计量supFT(l)、UDmax、WDmax和supFT(l+1|l)对模型(3)进行检验。其中，supFT(l)是检验是否存在结构突变假设的F统计量。UDmax=max[1,Max]supFT(l)为Double maximum statistic, WDmax= max[1,Max]wlsupFT(l)为Weighted double max statistic，Max表示结构突变数目的最大允许值。本文设定Max=8，截断值为0.1。UDmax和WDmax统计量是检验在给定结构突变数目的最大允许值Max时，是否存在未知数目的结构突变。序贯的supFT(l+1|l)统计量是检验在存在l个突变点的条件下是否存在第l+1个突变点。为了确定突变点的数目，本文首先利用UDmax和WDmax这两个统计量来确定是否至少存在一个突变点，如果存在突变点，我们再利用supFT(l+1|l)统计量来确定突变点的具体数目。

1.3 ARFIMAX-FIGARCH模型

Andersen等[5]的研究表明，ARFIMA(p,d,q)模型样本外预测能力要比基于低频收益率数据的GARCH模型、SV模型以及RiskMetrics方法的强。ARFIMA(p,d,q)模型可以表述为

Φ(L)(1-L)d(lnRVt-μ)=Θ(L)ut

(4)

其中Φ(L)=1-φ1L-φ2L2-…-φpLp，Θ(L)=1+θ1L+θ2L2+…+θqLq分别为自回归滞后p阶算子以及移动平均滞后q阶算子，(1-L)d为分数差分算子，μ表示对数已实现波动率的均值，假定{ut}为高斯白噪声。

为考虑波动率的杠杆效应，Giot等[7]将滞后期收益率以及正负收益的示性函数加入到ARFIMA(p,d,q)模型中，构建了如下式所述的ARFIMAX模型

Θ(L)ut

(5)

Beltrat等[9]首次考虑了ARFIMA模型残差的时变异方差性，构建的ARFIMA-FIGARCH模型也进一步提高了模型的样本外预测性能。Degiannakis[10]结合ARFIMAX模型以及门阀ARCH模型，构建的ARFIMAX-TARCH模型也取得了较好的预测效果。本文结合他们的建模思想，通过FIGARCH模型结构来捕获ARFIMAX模型(5)残差的时变异方差性方差及其长记忆性，构建ARFIMAX-FIGARCH模型来预测农产品期货市场的已实现波动率，该模型表述如下

Φ(L)(1-L)d·

ut=σu,tεt，

(6)

1.4 样本内检验

参照Rapach 等[21-22]的研究，本文的样本内检验分两步进行：首先，利用纯均值多突变模型检验每一种农产品期货品种的已实现波动率序列在总体区间的结构突变特征；然后，同时在总体样本区间以及由纯均值多突变模型所确定的子样本区间上估计ARFIMAX-FIGARCH模型。通过上述的样本内检验，可以分析我国农产品期货市场已实现波动率的结构突变特征，并且可以考察农产品期货市场已实现波动率的结构突变特征对于拟合ARFIMAX-FIGARCH模型的影响。更为重要的是，样本内检验结果可为后文的样本外预测分析提供了前提基础。

1.5 预测模型

本文首先将总体数据样本T划分为样本内和样本外两部分，其中样本内部分为前T1个交易日的数据样本，而样本外部分为最后T2个交易日的数据样本，所考虑的已实现波动率预测模型如下：

2)1倍滚动时间窗(Rolling Window)的ARFIMAX(1,d,1)-FIGARCH(1,du,1)模型。该模型采用滚动的估计窗口来重复估计ARFIMAX(1,d,1) -FIGARCH(1,du,1)模型并由此产生样本外预测值，估计窗口的大小固定为样本内数据样本数目T1。模型产生已实现波动率样本外预测值的方式基本类似于扩展时间窗的模型，唯一的区别在于为产生第t个已实现波动率的未来1天预测值的样本数据是基于t,…,T1+t-1，而扩展时间窗的模型是基于1,…,T1+t-1。

3)0.5倍滚动时间窗(Rolling Window)的ARFIMAX(1,d,1)-FIGARCH(1,du,1)模型。该模型获得已实现波动率的样本外预测值的方式与1倍滚动时间窗的模型类似，不同的是该模型将滚动的估计窗口大小固定为0.5T1，为产生第t个已实现波动率的未来1天预测值的样本数据是基于0.5T1+t,…,T1+t-1。

4)0.25倍滚动时间窗(Rolling Window)的ARFIMAX(1,d,1)-FIGARCH(1,du,1)模型。该模型获得已实现波动率的样本外预测值的方式与上述两类滚动时间窗(Rolling Window)的模型类似，不同的是该模型将滚动的估计窗口大小固定为0.25T1，获得第t个已实现波动率的未来1天预测值的样本数据是基于0.75T1+t,…,T1+t-1。

上述预测模型与Pesaran 等[23]和Rapach等[21-22]的研究不同的是：Pesaran 等[23]侧重于在结构突变条件下运用自回归模型预测宏观经济变量的条件均值，Rapach 等[21-22]侧重于在结构突变的条件下运用GARCH(1,1) 模型和GJR-GARCH(1,1)模型预测条件方差，而本文的研究侧重于在结构突变的条件下运用ARFIMAX-FIGARCH模型预测农产品期货市场的已实现波动率。

1.6 组合预测模型

Clark等[24]和Pesaran等[25]的研究表明，估计模型时加入结构突变点前的数据可以减少参数估计值的方差，因而在估计窗口中是否包含结构突变点前的数据存在一个偏差与效率的均衡问题，因此，本文基于Rapach等[21-22]的研究思想，在1.5节所述的5类ARFIMAX-FIGARCH模型得到的预测值的基础上构建线性组合预测模型和非线性组合预测模型，以适应农产品期货市场已实现波动率的结构突变特征。

文献中构建线性组合预测模型最简单的方法是对单项预测(Individual Forecasts)模型所获预测值取平均值，赋予所有单项预测值的权重都相等。参照Clark 等[24]的研究，主要考虑如下形式的简单线性组合模型：① CM组合(CM combined)法，这种组合预测方法是对扩展时间窗和0.25倍滚动时间窗的ARFIMAX(1,d,1)-FIGARCH(1,du,1)模型所得到的单项预测值取平均值；② 均值-窗口(Mean-windows)组合法，这种组合预测方法是对上述基于不同估计窗口的5类模型所得到的单项预测值取平均值；③ 切边均值-窗口(Trimmed mean-windows)组合法，该方法首先剔除上述5类模型所得的单项预测值中的最大和最小预测值，然后对剩余的3个单项预测值取均值。

构建线性组合预测模型的另一方法是采用线性回归法确定各个单项预测值的加权系数，表述如下

(7)

(8)

此外，本文还构建基于非参数核回归(Nonparametric kernel regression，NKR)的非参数组合预测模型和基于人工神经网络(Artificial neural networks，ANN)的组合预测模型。基于NKR的非参数组合预测模型可以表述为：

患者既往先后行两次剖宫产史，于第二次剖宫产术术中发现右侧卵巢包块，病检提示为恶性肿瘤，于剖腹产术后4天行右侧卵巢肿瘤根治术；1个月前因左侧股骨颈骨折，于我院行股骨颈骨折固定术；无输血及献血史，无高血压、糖尿病、慢性支气管炎等慢性疾病；预防接种史具体不详。曾有青霉素、头孢类药物过敏史。

(9)

参照Li等[26]的研究，模型(9)的参数由下式估计得到

(10)

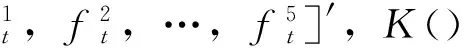
基于ANN的组合预测模型可以表述为

(11)

(12)

本文采用局部寻优反传算法(Backpropagation，BP)来估计模型(11)，通过不断更新模型的参数值直至达到预先设定的收敛性。

1.7 预测精度评价

参照Becker等[27]的研究，本文首先采用MSE和QLIKE的加总形式来评价和比较各类预测模型的预测精度。Patton[28]构建了一类对存在噪声的波动率代理变量稳健且同质度为b+2的损失函数，当b=0和b=-2时该损失函数分别为MSE和QLIKE。为了使实证评价结果更加稳健，本文还采用b=-1时的损失函数来评价和比较各类预测模型的预测精度，该损失函数与QLIKE类似，对低于实际预测值的惩罚度要重于超过实际预测值，但不对称性的程度要比QLIKE小。

MCS检验程序开始于总体模型集M=M0={1,…,m0}，然后反复检验预测精度相等(Equal forecasting accuracy ，EPA)的零假设

H0,M:E(dij,t)=0, ∀i,j∈M

(13)

参照Hansen等[29-30]的研究，本文在MCS检验过程中主要采用范围统计量TR和半二次统计量TSQ来检验EPA假设，这两类统计量可以表述为：

(14)

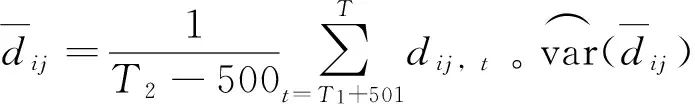
2 数据和描述性分析

本文研究的数据样本为黄豆期货、橡胶期货、豆粕期货以及强筋小麦期货的日内高频交易数据，取样区间为2003年8月1日～2012年8月31日，数据来源于Wind资讯金融数据库。由于在同一时间，对于每一个期货品种都有不同的合约在进行交易，本文按照交易最活跃的合约来构造主力连续期货合约。按照Bollerslev等[31]的建议，对日内高频交易数据进行每5分钟的抽样，以平衡测量误差和微观市场结构噪声对已实现波动率估计值的影响。剔除周末，公共节假日以及一些数据不全的交易日后得到黄豆期货主力连续期货合约总共T=2 198个交易日的5分钟高频数据，其他三类农产品期货主力连续合约的5分钟高频数据的交易日总数分别为2 182，2 195和2 200。

由表1的描述性统计量可知：① 农产品期货的日已实现波动率的标准差都比日收益率平方的标准差小，说明与收益率平方相比，已实现波动率是真实波动率的更加精确的估计量；② 农产品期货的日已实现波动率都表现出尖峰厚尾的特征，而日对数已实现波动率的无条件分布更为对称且峰度都较小，比日已实现波动率更加接近正态分布，因此，本文仅对对数形式的已实现波动率建模；③ 农产品期货的日收益率都表现出显著地不对称和尖峰特征，而日标准收益率更加接近正态分布；④ 由修正的Ljung-Box统计量可知，农产品期货的日收益率和日标准收益率在5%的置信水平下都找不到序列自相关的证据，而日收益率平方、日已实现波动率以及日对数已实现波动率在5%的置信水平下，都表现出显著的序列自相关特征，说明农产品期货的波动率具有较强地长记忆性；⑤ 由LM统计量可知，农产品期货的对数已实现波动率序列都表现出较强的ARCH效应。综上所述，近似正态、较强的序列自相关和ARCH效应是四类农产品期货对数已实现波动率的共同的典型特征，也是本文构建ARFIMAX-FIGARCH模型来预测农产品期货市场波动率的动机。

3 实证结果与分析

3.1 样本内估计结果与分析

由图1可知，黄豆期货和橡胶期货的对数已实现波动率序列在总体区间上存在5个结构突变点，豆粕期货和强筋小麦期货的对数已实现波动率序列存在4个结构突变点。从图1和表2给出的具体结构突变时点可知：四种农产品期货市场的结构突变点都与一连串的宏观面、政策面重大事件(结构突变点附近的重大事件可参阅Wind咨询的《证券市场大事记》)冲击有关，说明我国农产品期货市场也具有“政策市”的特征；四种农产品期货的对数已实现波动率的结构突变点与时间有所差异，其原因可能是不同农产品期货品种的投资者类型、信息不对称程度和需求弹性等因素导致了市场之间对重大事件的反应不同。

表2还给出了ARFIMAX(1,d,1)-FIGARCH(1,du,1) 模型在总体区间2003年8月1日～2012年8月31日以及由结构突变检验确定的子样本区间上的参数估计值。由总体区间上的参数估计值可知：① 参数b的估计值都显著为负，说明当前的坏消息(负收益率)对下一期波动率的影响效应要大于好消息(正收益率)，表明农产品期货市场存在明显的杠杆效应；② 农产品期货的对数已实现波动率序列的长记忆参数d的估计值在0.474(橡胶期货)到0.545(豆粕期货)之间，表明农产品期货的对数已实现波动率序列存在显著的长记忆性；③ “已实现波动率的波动率”(volatility of realized volatility)(参见文献[11])的长记忆参数du的估计值在0.45～0.47之间，表明农产品期货的对数已实现波动率的波动率也存在显著的长记忆性。

表1 描述性统计量

说明：日收益率为日内高频收益率的和；日标准收益率由日收益率除以日已实现波动率得到；修正的Ljung-Box统计量用来检验的零假设条件是前r个相关系数为0；ARCH LM统计量用来检验的零假设条件是从滞后1阶到q阶不存在ARCH效应。

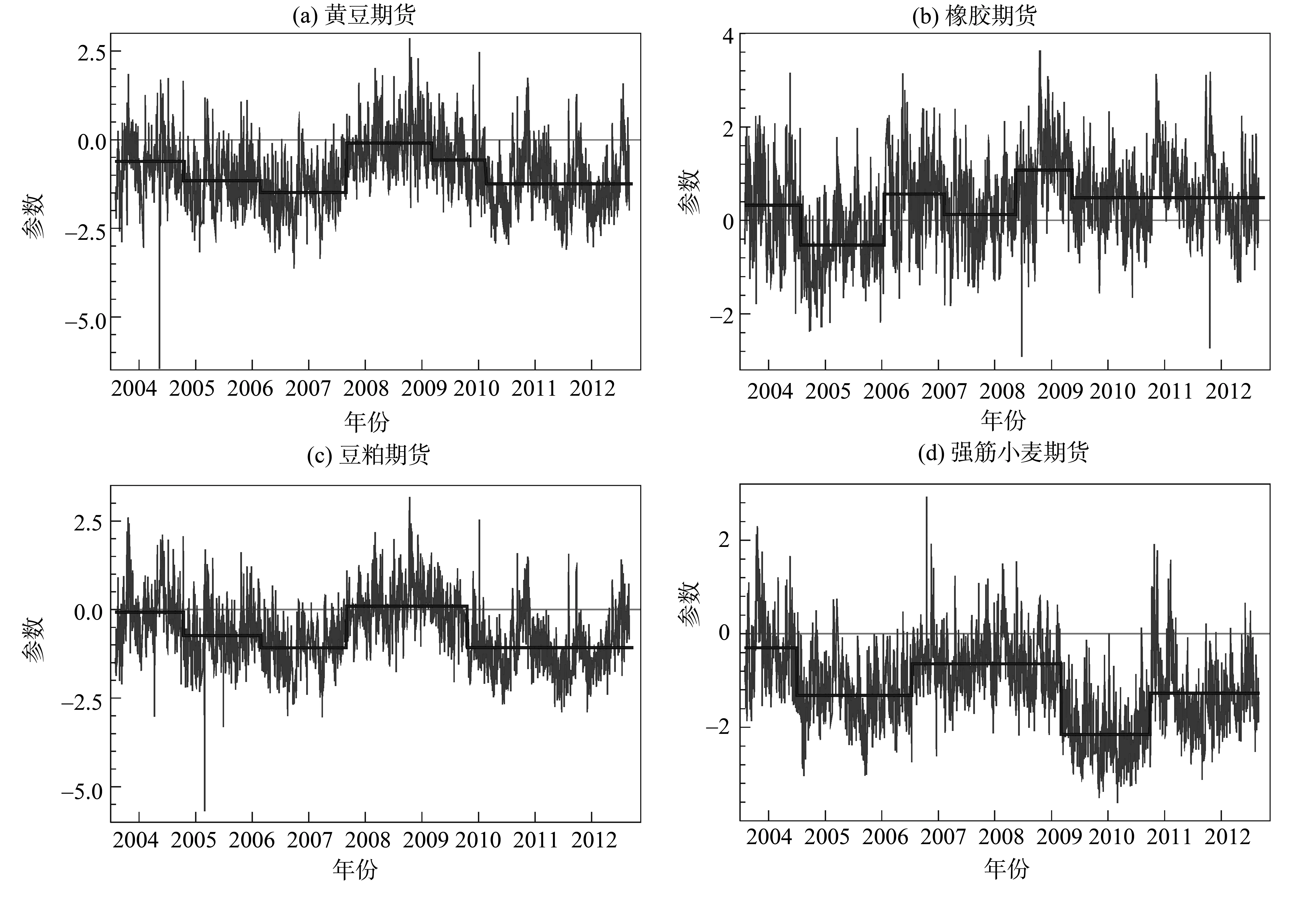
图1 对数已实现波动率以及各种状态下的均值估计Fig.1 Log realized variance and the estimations of mean for each of regimes

ARFIMAX(1,d,1)-FIGARCH(1,du,1) 模型在由结构突变检验确定的子样本区间上的参数估计值有较大的变化：① 参数b在各个子样本区间上的估计值的绝对值在绝大多数情况下都比总体区间上的估计值大，说明相对于总体区间而言，农产品期货市场的杠杆效应在子样本区间上更为明显；② 长记忆性参数d在由结构突变检验确定的各个子样本区间上的估计值在绝大多数情况下都比总体区间上的估计值小，并且在有些子样本区间上d的估计值的下降趋势非常大，这一发现表明，若不考虑农产品期货的已实现波动率的结构突变特征，能导致波动率序列长记忆性的过高估计；③ “已实现波动率的波动率”的长记忆参数du在各个子样本区间上的估计值往往也有较大的差别。由此可见，忽略农产品期货已实现波动率的结构突变特征会掩盖ARFIMAX(1,d,1)-FIGARCH(1,du,1) 模型的参数在不同时期的差异性，势必影响该模型对已实现波动率的预测性能。

3.2 样本外预测结果与分析

将总体数据样本区间2003年8月1日-2012年8月31日划分为样本内和样本外两部分，其中2003年8月1日～2008年7月24日为样本内部分，最后1 000个交易日数据(2008年7月25日-2012年8月31日)为样本外部分。本文采用“滚动时间窗”的估计方法获得在样本外区间上的组合预测值，具体实施过程如下：第一步，选取样本外区间上的前500个交易日的单项预测值作为第一个估计样本，分别估计模型(7)、模型(9)和模型(11)，以获得各类组合预测模型的组合加权系数估计值，将估计得到的加权系数对样本外区间上的第501个交易日的单项预测值进行加权组合，以获得第1个未来1天的已实现波动率的组合预测值。第二步，固定估计窗口的大小为500，将样本区间向后平移1天构成新的估计样本，重新估计各类组合预测模型的加权系数，并利用该估计值对第502个交易日的单项预测值进行加权组合，以获得第2个未来1天的已实现波动率的组合预测值。第三步，不断重复第二步，可以得到第3个、第4个……直到第500个未来1天的已实现波动率的组合预测值。对于所有的组合预测模型，不断重复估计模型500次，都可以获得500个未来1天的预测值。将样本外区间上第501个交易日至第1 000个交易日的农产品已实现波动率的估计值(由式(2)估计得到)作为真实波动率的代理来评价和比较各种预测方法(包括各种单项预测方法和组合预测方法)的预测精度。表3给出了所有单项预测模型和组合预测模型预测四种农产品期货的已实现波动率的3类损失函数值及其预测精度排名。

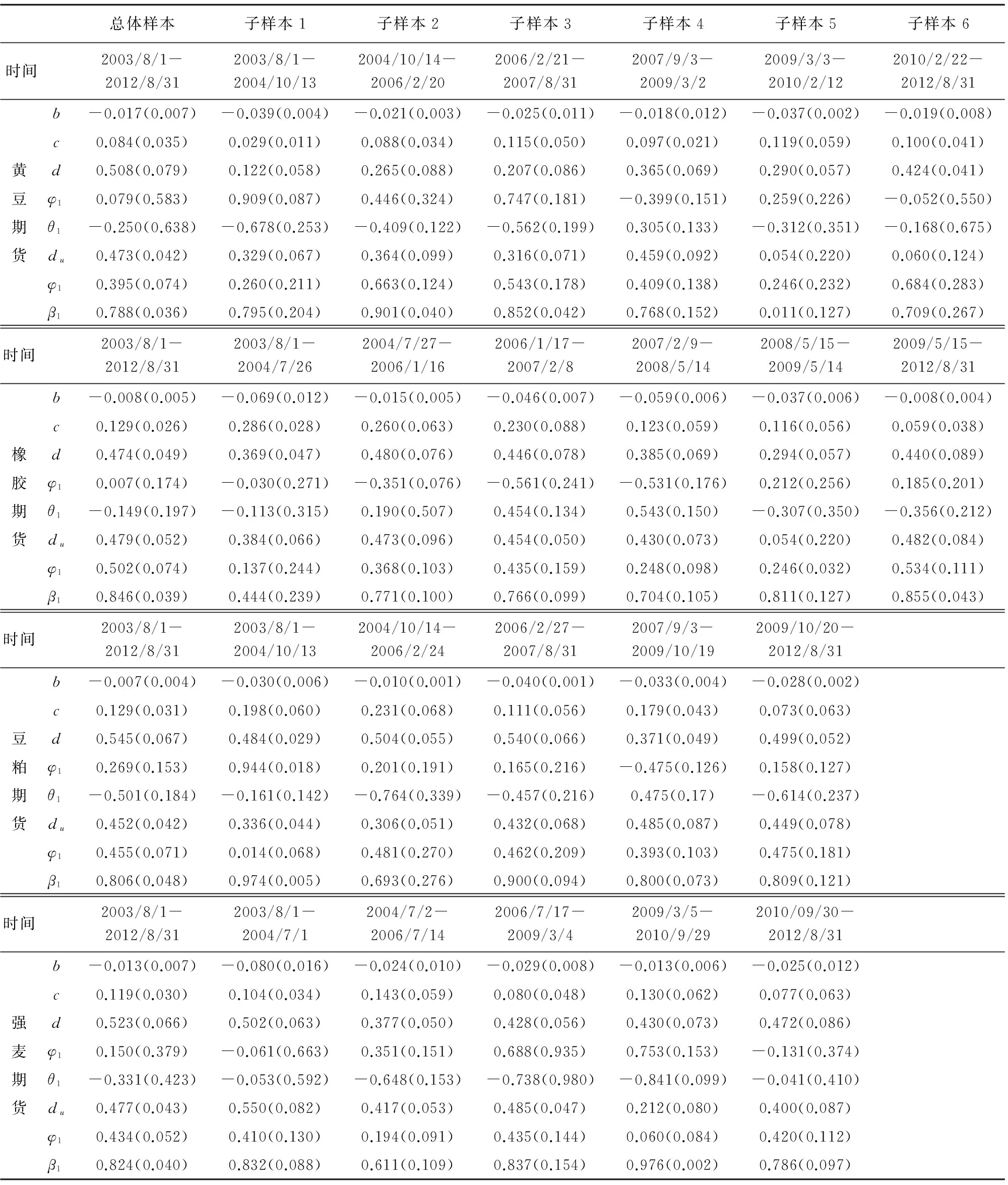
表2 ARFIMAX(1,d,1)-FIGARCH(1,du,1) 模型的估计结果

由表3可知：① 在所有损失函数评价标准下，基于滚动时间窗口和结构突变调整时间窗口的ARFIMAX(1,d,1) -FIGARCH(1,du,1) 模型对四种农产品期货的已实现波动率的预测精度并不一定比基于扩展时间窗口的ARFIMAX(1,d,1) -FIGARCH(1,du,1) 模型高，这一结果表明，确定一个特定的估计窗口使单项预测模型能够始终如一的产生最精确的波动率预测值是非常难的。② 在所有损失函数评价标准下，并不是所有的组合预测模型对四种农产品期货的已实现波动率的预测精度都一致性的比单项预测模型高。虽然具有相等加权系数的线性组合预测模型(包括CM组合法、均值-窗口组合法和切边均值-窗口组合法)对农产品期货的已实现波动率的预测精度在大多数情况下比基于扩展时间窗口的单项预测模型高，但在很多情况下都比滚动时间窗口和结构突变调整时间窗口的单项预测模型低。③ 在所有损失函数评价标准下，基于OLS、NRLS、ERLS和SIC的可变加权系数的线性组合预测模型以及基于非参数核回归NKR的非参数组合预测模型对四种农产品期货的已实现波动率的预测精度比所有单项预测模型和具有相等加权系数的线性组合预测模型高，说明具有时变权重的组合预测模型是结构突变条件下预测已实现波动率更有用的方法。④ 在所有的预测模型中，采用非参数核回归确定时变加权系数的非参数组合预测模型在3种损失函数评价标准下都具有最小的预测误差，说明非参数组合预测模型是所有预测模型中预测精度最高的模型；采用NRLS和SIC确定时变加权系数的线性组合预测模型的预测精度分别排在第2位和第3位，并且二者的预测精度十分接近，表明就四种农产品期货的已实现波动率而言，NRLS最小化了所有可能的线性组合预测模型的SIC值。⑤ 相对于其他组合预测模型而言，采用ANN确定时变加权系数的非线性组合预测模型在3中损失函数评价标准下对四种农产品期货的已实现波动率的预测精度表现都非常差，其原因可能是5种单项预测模型的预测误差之间存在高度相关性以至于ANN算法很难识别这种相关模式。

表4给出了所有预测模型在损失函数MSE、QLIKE以及b=-1时的稳健损失函数评价标准下的经过10000次bootstrap模拟过程后得到的MCS检验结果。由表4可知：就黄豆期货而言，在25%的置信水平下，模型置信集MCS在所有的损失函数评价标准下都只包含基于NKR的非参数组合预测模型以及基于NRLS和SIC的线性组合预测模型3类模型；就橡胶期货而言，在25%的置信水平下，模型置信集MCS在损失函数MSE和QLIKE下分别包含了5类和4类模型，而在10%置信水平和b=-1时的稳健损失函数评价标准下，仅包含基于NKR的非参数组合预测模型以及基于NRLS和SIC的线性组合预测模型3类模型；至于豆粕期货，在25%的置信水平下，模型置信集MCS在损失函数MSE和b=-1时的稳健损失函数下都仅包含基于NKR的非参数组合预测模型和基于NRLS的线性组合预测模型2类模型，而在损失函数QLIKE下，包含了基于NKR的非参数组合预测模型和基于NRLS和SIC的线性组合预测模型3类模型；就强麦期货而言，在25%的置信水平下，模型置信集MCS在损失函数MSE和损失函数QLIKE下都只包含基于NKR的非参数组合预测模型和基于NRLS和SIC的线性组合预测模型3类模型，而在b=-1时的稳健损失函数下，仅包含基于NKR的非参数组合预测模型和基于NRLS的线性组合预测模型2类模型。上述MCS检验结果表明：① 所有单项预测模型和具有相等加权系数的线性组合预测模型(包括CM组合法、均值-窗口组合法和切边均值-窗口组合法)都没有包含在模型置信集MCS中，这一结果进一步说明了，具有时变权重的组合预测模型是结构突变条件下预测已实现波动率更有用的方法；② 在10%的置信水平下，基于NKR的非参数组合预测模型和基于NRLS和SIC的线性组合预测模型几乎都包含在模型置信集MCS中，进一步说明，这3类模型是在结构突变条件下预测农产品期货市场波动率的预测性能最好的模型。

总体而言，结构突变检验结果显示我国农产品期货市场波动率普遍存在结构突变特征，该特征的普遍存在致使在实践中很难确定预测模型的最优估计窗口大小，而对基于不同估计窗口大小的ARFIMAX(1,d,1) -FIGARCH(1,du,1) 模型所得的单项预测值进行时变加权组合通常能够提供更准确的波动率预测值，并且基于NKR的非参数组合预测模型和基于NRLS和SIC的线性组合预测模型是在结构突变条件下预测农产品期货市场波动率尤其有效的方法。

表3 单项预测和组合预测的损失函数值

(续表3)

模型黄豆期货ValueRank橡胶期货ValueRank豆粕期货ValueRank强麦期货ValueRankMean-windows0.155190.1939100.219490.243710Trimmedmean-windows0.155080.193480.2195100.24329OLS0.141250.192750.215650.23645NRLS0.133220.191320.208620.23012ERLS0.140140.192340.214040.23384WLSP0.1488130.193790.219070.23956SIC0.133830.191630.209630.23083非线性组合预测ANN0.1641150.2021150.2268150.296615NKR0.130710.191010.202510.22921

1)单项预测：基于不同估计窗口的ARFIMAX(1,d,1)-FIGARCH(1,du,1)模型

表4 预测模型的MCS检验结果

(续表4)

模型黄豆期货TRTSQ橡胶期货TRTSQ豆粕期货TRTSQ强麦期货TRTSQ损失函数:b=-1Expandingwindow0.0000.0000.0000.0000.0280.0240.0000.000Rollingwindow0.0000.0000.0100.0050.0040.0020.0000.0000.5rollingwindow0.0010.0010.0010.0000.0000.0000.0010.0000.25rollingwindow0.0080.0070.0130.0120.0120.0100.0070.006Breaks0.0080.0060.0000.0000.0150.0120.0110.009CMcombined0.0010.0000.0010.0000.0000.0000.0010.001Mean-windows0.0030.0020.0030.0010.0010.0000.0020.001Trimmedmean-windows0.0030.0020.0070.0050.0030.0020.0040.004OLS0.0150.0120.0270.0180.0250.0240.0560.052NRLS0.218*0.224*0.540**0.532*0.775**0.760**0.628**0.615**ERLS0.0320.0280.0550.0480.0660.0640.0640.062WLSP0.0000.0000.0030.0010.0090.0080.0570.054SIC0.150*0.144*0.212*0.205*0.182*0.180*0.114*0.112*ANN0.0000.0000.0000.0000.0000.0000.0000.000NKR1.000**1.000**1.000**1.000**1.000**1.000**1.000**1.000**

4 研究结论

我国农产品期货市场是新兴市场，易受外来宏、微观因素以及季节因素的影响，市场波动率常常会发生区制转换或结构突变，而这种结构突变又会造成市场波动的长记忆性的过高估计，进而影响市场波动率的预测精度。因此，深入分析我国农产品期货市场波动率的结构突变特征，并构建适合我国农产品期货波动率特征的预测模型，对于风险管理人员能够相对准确的度量和预测未来市场风险和套期保值者能够更加及时地防范市场波动等都有重要的理论和现实意义。本文在检验农产品期货已实现波动率序列的结构突变等特征基础上，通过构造不同估计窗口大小的ARFIMAX-FIGARCH模型及其线性和非线性组合预测模型来预测农产品期货市场的已实现波动率，并采用基于自助法的MCS检验评价和比较各类预测模型的预测性能。研究结果表明：① 农产品期货的已实现波动率序列在总体样本区间上都表现出结构突变特征、杠杆效应以及双长记忆性，并且结构突变点都与一连串的宏观面、政策面重大事件冲击有关，说明了我国农产品期货市场与股票市场一样也具有“政策市”的特征。② ARFIMAX(1,d,1)-FIGARCH(1,du,1) 模型的参数在由结构突变检验确定的子样本区间上的估计值与总体区间上的估计值存在较为显著的差别，其中，杠杆效应参数b在各个子样本区间上的估计值的绝对值在绝大多数情况下都比总体区间上的估计值大，说明农产品期货市场的杠杆效应在子样本区间上更为明显，而长记忆性参数d的在各个子样本区间上的估计值在绝大多数情况下都比总体区间上的估计值小，说明农产品期货市场波动率的长记忆性在子样本区间上较弱。③ 在所有损失函数评价标准下，基于滚动时间窗口和结构突变调整时间窗口的ARFIMAX(1,d,1) -FIGARCH(1,du,1) 模型对四种农产品期货的已实现波动率的预测精度并不一定比基于扩展时间窗口的模型高，这一结果说明，结构突变致使在实践中很难确定单项预测模型的最优估计窗口大小。④ 对基于不同估计窗口大小的ARFIMAX(1,d,1) -FIGARCH(1,du,1) 模型所得的单项预测值进行时变加权组合通常能够提供更准确的波动率预测值，并且基于NKR的非参数组合预测模型和基于NRLS和SIC的线性组合预测模型是在结构突变条件下预测农产品期货市场波动率尤其有效的方法。

[1] 王辉, 孙志凌, 谢幽篁. 中国农产品期货套期保值非对称效应研究[J]. 统计研究, 2012, 29(7): 68-74.

[2] 王金媛. 我国农产品期货价格波动率分析[J]. 东北农业大学学报：社会科学版, 2009, 7(3): 30-31.

[3] 魏宇. 中国商品期货市场的风险价值模型及其后验分析[J]. 财贸经济, 2009, 2: 63-68.

[4] 刘向丽, 成思危, 汪寿阳, 等. 基于ACD模型的中国期货市场波动性[J]. 系统工程理论与实践, 2012, 32(2): 268-273.

[5] ANDERSEN T G, BOLLERSLEV T, DIEBOD F X, et al. Modeling and forecasting realized volatility [J]. Econometrica, 2003, 71: 579-625.

[6] CORSI F. A simple approximate long memory model of realized volatility [J]. Journal of Financial Econometrics, 2009, 7: 174-196.

[7] GIOT P, LAURENT S. Modeling daily value-at-risk using realized volatility and ARCH type models [J]. Journal of Empirical Finance, 2004, 11: 379-398.

[8] CORSI F, RENO R. HAR volatility modeling with heterogeneous leverage and jumps [D]. University of Siena, 2009.

[9] BELTRATTI A, MORANA C. Statistical benefits of value-at-risk with long memory [J]. Journal of Risk, 2005, 7: 21-45.

[10] DEGIANNAKIS S. ARFIMAX and ARFIMAX-TARCH realized volatility modeling [J]. Journal of Applied Statistics, 2008, 35: 1169-1180.

[11] CORSI F, MITTNIK S, PIGORSCH U. The volatility of realized volatility [J]. Econometric Reviews, 2008, 27: 46-78.

[12] MARTEN M, DIJK D, MICHIEl P. Forecasting S&P500 volatility: long memory, leverage effects, day-of-the-week seasonality, and macroeconomic announcements [J]. International Journal of Forecasting, 2009, 25(2): 282-303.

[13] 王春峰，庄泓刚，房振明，等. 长记忆随机波动模型的估计与波动率预测[J]. 系统工程，2008，26(7)：29-34.

[14] 魏宇. 金融市场的多分形波动率测度、模型及其SPA检验[J]. 管理科学学报，2009，12(5)：88-99.

[15] 杨科，陈浪南. 股市波动率的短期预测模型和预测精度评价[J]. 管理科学学报，2012, 15(5): 19-31.

[16] ANDERSEN T G, BOLLERSLEV T. Answering the skeptics: yes, standard volatility models do provide accurate forecasts [J]. International Economic Review, 1998, 39: 885-905.

[17] MARTENS M. Measuring and forecasting S&P 500 index‐futures volatility using high‐frequency data [J]. Journal of Futures Markets, 2002, 22(6): 497-518.

[18] CHOI K, YU W C, ZIVOT E. Long memory versus structural breaks in modeling and forecasting realized volatility [J]. Journal of International Money and Finance, 2010, 29(5): 857-875.

[19] BAI J, PERRON P. Estimating and testing linear models with multiple structural changes [J]. Econometrica, 1998, 66: 47-78.

[20] BAI J, PERRON P. Computation and analysis of multiple structural changes model [J]. Journal of Applied Econometrics, 2003, 18: 1-22.

[21] RAPACH D E, STRAUSS J K. Structural breaks and GARCH models of exchange rate volatility [J]. Journal of Applied Econometrics, 2008, 23(1): 65-90.

[22] RAPACH D E, STRAUSS J K, WOHAR M E. Forecasting stock return volatility in the presence of structural breaks [J]. Forecasting in the Presence of Structural Breaks and Model Uncertainty (Frontiers of Economics and Globalization, Volume 3), Emerald Group Publishing Limited, 2009, 3: 381-416.

[23] PESARAN M H, TIMMERMANN A. Small sample properties of forecasts from autoregressive models under structural breaks [J]. Journal of Econometrics, 2005, 129(1): 183-217.

[24] CLARK T E, MCCRACKEN M W. Improving forecast accuracy by combining recursive and rolling forecasts [J]. International Economic Review, 2009, 50(2): 363-395.

[25] PESARAN M H, TIMMERMANN A. Selection of estimation window in the presence of breaks [J]. Journal of Econometrics, 2007, 137(1): 134-161.

[26] LI F, TKACZ G. Combining forecasts with nonparametric kernel regressions [J]. Studies in Nonlinear Dynamics & Econometrics, 2005, 8(4):Article 2.

[27] BECKER R, CLEMENTS A E. Are combination forecasts of S&P 500 volatility statistically superior?[J]. International Journal of Forecasting, 2008, 24(1): 122-133.

[28] PATTON, A. Volatility forecast comparison using imperfect volatility proxies [J]. Journal of Econometrics, 2011, 160: 246-256.

[29] HANSEN P R, LUNDE A, NASON J M. Choosing the best volatility models: the model confidence set approach [J]. Oxford Bulletin of Economics and Statistics, 2003, 65: 839-861.

[30] HANSEN P R, LUNDE A, NASON J M. The model confidence set [J]. Econometrica, 2011, 79(2): 453-497.

[31] BOLLERSLEV T, LITVINOVA J, TAUCHEN G. Leverage and volatility feedback effects in high-frequency data [J]. Journal of Financial Econometrics, 2006, 4: 353-384.