弱耗散的Degasperis-Procesi方程弱解的存在性*

关春霞，冯兆永

(1. 广东工业大学应用数学学院, 广东 广州 510006；2. 中山大学数学与计算科学学院, 广东 广州 510275)

在本文中我们主要研究如下的弱耗散Degasperis-Procesi方程

ut-utxx+4uux+λ(u-uxx)=3uxuxx+uuxxx,

t>0,x∈R

(1)

其中λ>0。当t=0时，u满足初始条件

u(0,x)=u0(x),x∈R

(2)

Degasperis等[1]通过对水波方程的研究得到了如下的Degasperis-Procesi方程

(3)

它具有双Hamiltonian结构可积方程并且有无穷多个守恒律和无穷多对尖峰孤立子解[1]，所以引起了很多数学家和物理学家的关注[2-13]。

当初值在Hs(其中s>3/2)时，殷朝阳[5-6]分别证明了Degasperis-Procesi方程的直线上和周期局部适定性问题, 并且得到了爆破机制和爆破结果。Liu和殷朝阳等[7-8,11]研究了方程(3)的整体强解的存在性，并证明了在初值满足一定的符号条件时整体强解的唯一性。Coclite等[12]证明了初值在L2(R)∩L4(R)中方程(3)弱解的存在性。

耗散的Degasperis-Procesi方程具有如下的形式：

其中L(u)是耗散项。一般情况下，L是和物理量有关的拟线性微分算子。在本文中，L(u)=λ且λ>0是个常数。

Wu等[14-15]研究了方程(1)的爆破和解的衰退。方程(1)强解的整体存在性也有结果[13,16]。方程(1)的弱解情况亦有人研究，Guo等[17]证明了如下结果：如果初值

令m=u-uxx, 我们可以把方程(1)改写为

mt+mxu+3mux+λm=0,t>0,x∈R

(4)

(5)

本文的主要结果是证明方程(1)熵弱解的存在性，在给出主要结论之前，我们先给出弱解以及熵弱解的定义。

定义1u称为方程(1)满足Cauchy问题(2)的弱解，如果u(t,x)∈L∞((0,∞);L2(R))并且在R+×R上的分布意义下(即在(D′(R+×R)中)满足方程(5) 和当λ→0时,u(t,·)→u0。定义2u称为方程(1)满足Cauchy问题(2)的熵弱解，如果u是方程(1) 满足Cauchy问题(2)的弱解, 并且对于任意凸的C2熵函数η：R→R和对应的熵对q: R→R，q′(u)=uη′(u), 在空间(D′(R+×R)以下等式成立

∂tη(u)+∂xq(u)+λq(u)+

(6)

下面给出本文的主要结论：

定理1 设u0∈L2(R)∩L4(R), 则Cauchy问题 (1)-(2)至少存在一个熵弱解，并且u满足以下的条件：

对于任意的t>0, 且有

本文结构如下安排：第1节我们给出方程(1)的粘性逼近解uε并得到关于uε的基础能量估计。第2节证明uε存在强收敛子列，并证明其子列收敛极限即为方程的熵弱解。

1 粘性逼近解的存在性和估计

本节中, 我们构建方程(1)的粘性逼近解uε=uε(t,x), 即uε为以下方程的解

t>0,x∈R

(7)

满足初始条件

u(0,x)=uε,0(x),x∈R

(8)

这里uε,0(x)=(φε*u0)(x)∈Hs(R)，s≥2，并且

如果u0∈L2(R)∩L4(R)，那么对任意的p∈[2,4]，有

‖uε,0‖Lp(R)≤‖u0‖Lp(R),∀ε>0

并且，当ε→0时，

uε,0→u0,在空间Lp(R)中

下面给出粘性解uε的存在性引理。

引理1 设u0∈L2(R)，则方程(7)-(8)存在唯一的强解uε∈C(R+;Hs(R)),s≥2。

证明任意固定的T>0和(t,x,u)∈[0,T)×R×R，记

h(t,x,u)=0,a(t,x,u)=ε

则文[17]中定理2.3的所有条件均满足，则根据文[17]中的定理2.3的结论，我们知道存在唯一的解uε∈C([0,T);Hs(R)),s≥2为方程(7)-(8)的强解。由T的任意性我们得uε∈C(R+;Hs(R))。

接下来，我们给出uε的一致L2(R)估计, 此估计是本文中最基础的能量估计。

引理2 设u0∈L2(R)，对于任意固定的ε>0，则当t>0时，以下的估计成立：

并且有

4(vε(t,x))2)dx+

4(vε(t,x))2)dxds≤

4(vε(0,x))2)dx

(9)

和

4(vε(t,x))2)dx≤

4(vε(0,x))2)dx

(10)

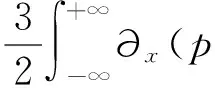
和文[12]中引理2.3的证明类似, 我们有

和

由于λ>0, 则根据分部积分，可得到

故有

和

对以上两个不等式在[0,t]上积分, 就可得到式(9)和式(10)。

通过文[12]中引理 2.2的证明, 我们有

和

5(∂xvε(0,x))2+4(vε(0,x))2)dx

从而利用式(9)、式(10)可得到

(11)

和

则由式(11)，有

此引理得证。

‖Pε(t,·)‖L1(R)≤

(12)

‖∂xPε(t,·)‖L1(R)≤

(13)

这里用到了‖p‖L1(R)=1和‖∂xp‖L1(R)=1。再次应用 Hölder不等式和引理2，还可以得到

(14)

以及

(15)

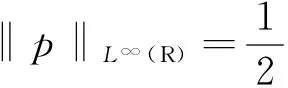
(16)

接下来，我们证明粘性逼近解在L4中一致有界。

引理3 设u0∈L2(R)∩L4(R)，对于任意固定的ε>0，则当t>0时, 有

*(uε)2)dx-

利用 Hölder不等式以及式 (11)、式(15)，可推出

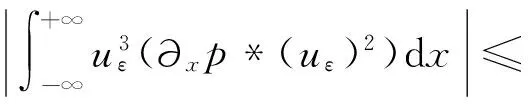
利用分部积分，得到

又因为λ>0, 则可得到

此不等式可以改写为如下形式

则由 Gronwall’s不等式, 即可得到

此不等式经过一个简单的移项即可得到此引理的结论。

注1 文[12]中对应的结果是本文中引理2中当λ→0时的特殊情况。

2 熵弱解的存在性

以第1节中的估计为基础，在本节中我们首先给出粘性解的一致先验估计，然后证明其强收敛性，最后证明粘性逼近解的极限即为方程(1)的弱解。

为了证明我们的结果，首先给出两个引理。

引理5[19]设Ω是R+×R中的有界开集。对某个s≥0,f∈C2(R)满足：

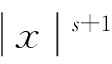
meas{x:f″(x)=0}=0

定义Il,fl,Fl:R→R满足如下条件：

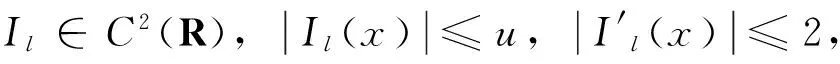
现在给出本节的一个主要结果。

u∈L∞(R+;L2(R))∩L∞(0,T;L4(R))

(17)

并且当k→∞时，有

uεk→u,在空间Lp((0,T)×R)中,∀p∈[2,4)

(18)

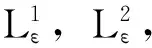
(19)

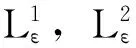
事实上，在方程(7)两边同时乘以η′(u)，根据链式法则可得

∂tη(uε)+∂xq(uε)+η′(uε)∂xPε+λq′(uε)=

(20)

根据引理2， 可得到

‖ε∂xη(uε)‖L2(R+×R)≤

再次根据引理2以及式(13), 得

和

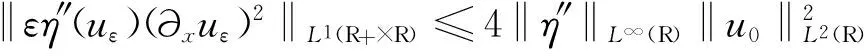
uεk→u,在空间Lp((0,T)×R)中,∀p∈[2,4)

此引理得证。

由引理6，我们就可以来证明定理1了。

Lq((0,T)×R)×Lp((0,T)×R)

(21)

从而要证明u是方程的弱解，由方程的形式知，只需证明: 当k→∞时，在空间(D ′(R+×R)中，有

也即只需证

(22)

事实上，由式(21)和 Hölder不等式, 知当k→∞时，有

根据引理5-6, 我们知道u满足定理1中的条件(i)-(iii)。因此本文结论成立。

[1] DEGASPERIS A, HOLM D D, HONE A N W. A new integral equation with peakon solutions [J]. Theo Math Phys, 2002, 133: 1463-1474.

[2] HOLM D D, STALEY M F. Wave structure and nonlinear balances in a family of evolutionary PDEs [J]. SIAM J Appl Dyn Syst, (electronic), 2003, 2: 323-380.

[3] LENELLS J. Traveling wave solutions of the Degasperis-Procesi equation [J]. J Math Anal Appl, 2005, 306: 72-82.

[4] LUNDMARK H. Formation and dynamics of shock waves in the Degasperis-Procesi equation [J]. Inverse Problems, 2003, 19: 1241-1245.

[5] YIN Z. On the Cauchy problem for an integrable equation with peakon solutions [J]. Illinois J Math, 2003, 47(3): 649-666.

[6] YIN Z. Global existence for a new periodic integrable equation [J]. J Math Anal Appl, 2003, 49: 129-139.

[7] YIN Z. Global weak solutions to a new periodic integrable equation with peakon solutions [J]. J Funct Anal, 2004, 212: 182-194.

[8] YIN Z. Global solutions to a new integrable equation with peakons [J]. Indiana Univ Math J,2004, 53: 1189-1210.

[9] COCLITE G M, KARLSEN K H, HOLDEN H. Well-posedness for a parabolic-elliptic system [J]. Discrete Contin Dyn Systems, 2005, 13: 659-682.

[10] MATSUNO Y. Multisoliton solutions of the Degasperis-Procesi equation and their peakon limit [J]. Inverse Problems, 2005, 21: 1553-1570.

[11] LIU Y, YIN Z. Global existence and blow-up phenomena for the Degasperis-Procesi equation [J]. Commun Math Phys, 2006, 267: 801-820.

[12] COCLITE G M, KARLSEN K H. On the well-posedness of the Degasperis-Procesi equation [J]. J Funct Anal, 2006, 233: 60-91.

[13] HENRY D. Infinite propagation speed for the Degasperis-Procesi equation [J]. J Math Anal Appl, 2005, 311: 755-759.

[14] WU S, YIN Z. Blow-up and decay of the solution of the weakly dissipative Degasperis-Procesi equation [J]. SIAM J Math Anal, 2008, 40: 475-490.

[15] WU S, YIN Z. Blow-up phenomena and decay for the periodic Degasperis-Procesi equation with weak dissipation [J]. J Nonlinear Math Phys, 2008, 15: 28-49.

[16] GUO Z. Some properties of solutions to the weakly dissipative Degasperis-Procesi equation [J]. J Differential Equations, 2009, 246(11): 4332-4344.

[17] GUO Y, LAI S, WANG Y. Global weak solutions to the weakly dissipative Degasperis-Procesi equation [J]. Nonlinear Analysis: TMA, 2011, 74(15): 4961-4973.

[18] SCHONBEK M. Convergence of solution to nonlinear dispersive equations [J]. Communications in Partial Differential Equations, 1982, 7: 959-1000.

[19] LU Y. Convergence of solutions to nonlinear dispersive equations without convexity conditions [J]. Applicable Analysis: An International Journal, 1989, 31: 239-246.