湿度传感器的SVM温度补偿研究及软件设计
高大惟,刘建玲
(1.南京信息工程大学公共管理学院,江苏南京 210044;2.河北省玉田县气象局,河北唐山 064100)
0 引言
高分子湿敏电容器是近年来在气象湿度测量中应用最广泛的传感器,但是湿敏元件要长期暴露在空气中,线性度和抗污染,性能较差,很容易受到污染影响其测量准确度。同时温度的变化对湿敏电容影响大,是导致测量误差的主要原因之一,所以对湿度传感器进行温度补偿是必要的[1-2]。
典型BP神经网络常被用于传感器的误差补偿中,但易陷入局部极小,其求得网络最优的可能性小[3-4]。支持向量机是以结构风险最小化为准则的机器学习方法,较好地解决了非线性、局部极小等问题[3]。但是支持向量机的参数选择是难点,传统的经验和试凑法使得参数选择不准确,预测精度差,网格寻优方法则耗时长[5-6]。文中将改进的粒子群算法(PSO)用于支持向量机(SVM)的参数寻优,建立了湿度传感器的温度补偿模型,验证了粒子群支持向量机在湿度传感器温度补偿上的有效性,并通过与其他SVM参数寻优方法进行对比验证了改进粒子群算法的优越性,并利用MATLAB GUI设计了方便有效的湿度传感器温度补偿软件。
1 湿度传感器的SVM温度补偿
湿度传感器受环境湿度和温度因素影响,一般采用逆向建模的方法对其进行非线性补偿以消除温度的影响。文中利用支持向量机函数作为传感器的补偿环节,来逼近湿度传感器模型的非线性关系函数,使补偿后的输出具有理想特性,如图1所示。

图1 湿度传感器的支持向量机温度补偿原理
支持向量机非线性回归通过一个非线性映射函数φ将样本映射到高维特征空间中,在高维空间进行线性回归运算,从而获得原输入空间的非线性回归效果[7]。非线性回归问题转化为求下面的优化问题。
(1)
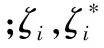
文中选用径向基核函数,利用Lagrange乘子法解决上述问题就可以最终得到如下回归函数。
(2)
(3)
2 粒子群优化支持向量机
SVM参数选择直接影响预测精度,用PSO对参数进行寻优使得参数选择具有目的性[8]。惯性权重w是PSO可调节参数中最重要的参数,较大的w使算法具有较强的全局收敛能力,较小的w使算法具有较好的局部收敛能力。因此,随着迭代次数的增加,w应该不断减小,这样能够防止PSO算法前期容易出现早熟收敛,后期易在全局最优值附近震荡的现象。文献[9]采用线性递减权重法让w从最大线性减到最小值,它把种群的进化看成是均匀的过程,但实际大多是非线性的,进化中每代所需的比例关系并不一定相同,所以线性递减权重方法不能描述复杂的非线性寻优问题,文中采用非线性的递减惯性权重加以改进,计算公式如下:
(4)
式中:wmax、wmin,表示为惯性权重w的最大值、最小值;t为当前迭代次数;tmax为最大迭代次数;k为常数。
这样在进化初期w较大,随着迭代次数的增加,w快速下降,算法前期有较强的全局搜索能力、后期要有较强的局部搜索能力,实现了PSO算法全局搜索和局部开发能力之间的平衡。利用改进的粒子群算法(AMPSO)对SVM参数寻优过程如图2所示。

图2 AMPSO-SVM算法流程图
3 湿度传感器温度补偿实例
文中的研究对象是自动气象站广泛使用的HMP45D温湿集成传感器,对传感器进行逐温度点、逐湿度点测试并采集数据。传感器的输出电压0~1 V与湿度值0~100%RH相对应,将多次测量的平均值作为实验数据[10]。实验选取的温度范围为-30~40 ℃,湿度为10%~95%RH,如图3所示,在没有温度补偿的情况下测得的湿度数据误差较大,不能达到使用要求。
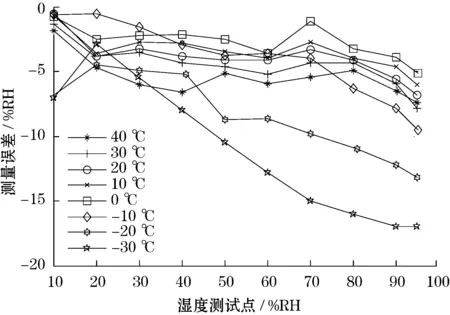
图3 湿度传感器测量误差随温度变化曲线
将传感器标定数据分为训练和测试2个样本,对训练样本进行SVM温度补偿,利用得到的数学模型对测试样本进行预测。训练样本为图3中的80组样本,测试样本为不同温湿度下互不相关的64组数据。
利用SVM将湿度传感器测得的温度值和湿度值作为输入,将标准湿度值作为输出。利用式(5)将数据归一化到(-1,1)区间。其中xmax、xmin为x的最大值和最小值。ymax为1,ymin为-1,y为归一化后的数据。
(5)
在libsvm中,3个待优化的SVM参数是:惩罚参数C、径向基核函数参数gamma=1/(2σ2)、不敏感损失函数系数ε.分别用c、g、p表示,SVM训练得到的最佳参数为bestc、bestg、bestp。表1为改进粒子群算法基本参数设置。

表1 改进粒子群算法基本参数设置
适应度函数为SVM训练样本的均方误差(mse)。假设f(xi)为实际输出,yi为期望输出,n为样本数目。适应度函数(fitness)为:
(6)
改进粒子群支持向量机训练得到的适应度曲线如图4所示。改进的粒子群支持向量机(AMPSO-SVM)、网格寻优支持向量机(GRID-SVM)以及遗传算法支持向量机(GA-SVM)3种方法的参数选取结果如表2所示。表3为样本均方误差。表4为3种方法运行时间对比。
3种方法对训练及测试样本的相对误差(Er)结果如图5所示。Er计算公式如下:

(7)

图4 改进粒子群支持向量机适应度曲线

表2 SVM参数选取结果

表3 样本均方误差
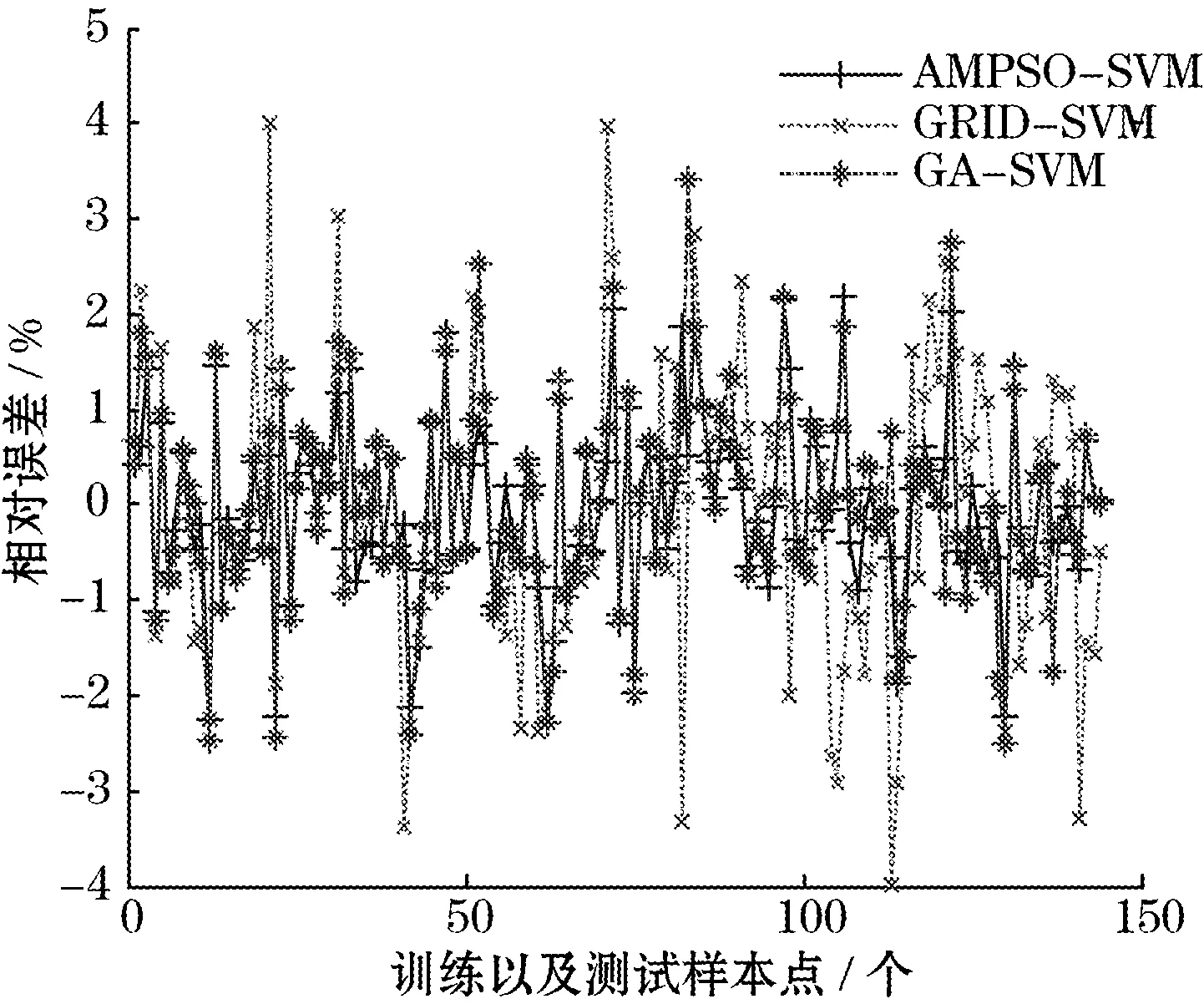
图5 3种方法相对误差曲线

表4 3种方法运行时间对比 s
由图5可以看出,3种方法都能够改善湿度传感器受温度影响导致精度下降问题,其中AMPSO-SVM的补偿效果最好,相对误差绝对值都在3%之内。从表3可以看出,AMPSO-SVM对样本的均方误差最小,说明AMPSO-SVM的补偿和泛化能力均优其他2种方法。从表4可以看出,改进的粒子群算法对SVM进行参数寻优的时间最短。综上可知,文中改进的AMPSO-SVM算法能够有效补偿温度对湿度传感器的影响,而且训练的速度和补偿的精度都要优于其他算法。

图5 3种方法相对误差曲线
4 湿度传感器的温度补偿软件设计
湿度传感器的SVM温度补偿软件是采用MATLAB的自带的图形用户界面GUI开发的。软件功能流程图如图6所示,运行效果如图7所示。

图6 软件功能流程图

图7 软件运行效果图
5 结束语
将改进的非线性惯性权重粒子群算法用于支持向量机的参数选择,建立了湿度传感器的温度补偿模型,并与网格寻优支持向量机方法和遗传算法支持向量机方法进行了比较。AMPSO-SVM方法的预测结果的相对差均小于3%,符合湿度传感器精度要求,有效改善了温度对湿度测量的影响,并且补偿精度和收敛速度都要优于其他2种方法。说明改进的粒子群支持向量机方法用于湿度传感器的温度补偿是有效可行的,同时湿度传感器的SVM温度补偿软件界面友好,操作方便,具有很强的实用性。
参考文献:
[1] 张伟星,王晓蕾,陈晓颖,等.电子探空仪气压传感器特性.解放军理工大学学报,2011,12(6):696-701.
[2] 芦俊,陈俊杰,颜景平.基于遗传算法的传感器系统的非线性校正.仪表技术与传感器,2001(6):38-40.
[3] 周燕.遗传算法与BP神经网络相结合的说话人识别系统.传感器与微系统,2009,28(6):98-103.
[4] 袁楚明,廖圣华,刘繄,等.光纤传感器的神经网络光强补偿及非线性校正.仪表技术与传感器,2012(2):108-110.
[5] 于雷,辛晓越,卢志泳,等.基于SVM的人体运动状态检测.计算机科学,2013,40(6):166-172.
[6] 强生杰,孔令刚.压力传感器的支持向量机非线性回归建模.传感器与微系统,2012,31(4):50-52.
[7] 李彦,梁正桃,李立京,等.基于小波和支持向量机的光纤微振动传感器模式识别.传感器与微系统,2013,32(2):43-49.
[8] 杨柳松,何光宇.基于改进粒子群优化的 SVM 故障诊断方法.计算机工程,2013,39(3):187-196.
[9] SHI Y,EBERHART R C.Empirical study of particle swarm optimization.Proceedings of the IEEE Congress on Evolutionary Computation,1999:1945-1950.
[10] 蔡兵.基于RBF神经网络的湿度传感器建模方法.仪表技术与传感器,2005(10):54-55.

