全对称振动陀螺的结构设计与参数优化分析

陈泓伍，陈玺浩，彭 晨，胡松奇，冷建兴

(1.浙江大学海洋学院，浙江杭州 310058；2.电子科技大学机电学院，四川成都 611731)

0 引言

陀螺仪是一种即使无外界参考信号也能探测出运载体本身姿态和状态变化的内部传感器，其具体功能是敏感运动体系的角度、角速度和角加速度[1]。作为一种重要的惯性敏感器件，陀螺仪是导航、制导、稳定、瞄准等系统的核心部件，广泛应用于航天飞行器[2]、汽车安全、工业自动化以及消费电子等领域[3]。目前陀螺主要有机械陀螺、光学陀螺、振动陀螺等传统陀螺以及近来发展起来的微机械电子系统陀螺(简称微机械陀螺)[4-5]。振动陀螺具有所有的惯性品质，可以实现微型化。振动陀螺发展迅速，低成本、高性能的振动陀螺一直是学术界研究热点。

文中研制了一种新型全对称结构的振动陀螺，依据振动陀螺工作原理，采用压电驱动和压电检测的方式，设计了结构模型，通过对陀螺模态的有限元分析，完成了陀螺结构参数优化，并进行了样机制作和试验验证。该陀螺与已有固态振动陀螺相比，体积小，结构完全对称，加工简单方便，惯性质量大，有利于提高陀螺灵敏度，具有较好的应用前景。

1 全对称振动陀螺的工作原理和结构设计

1.1 振动陀螺的工作原理

振动陀螺的简化模型如图1所示。质量块m固连在旋转坐标系的xy平面内，模型具有2个正交的振动模式，每个模式都简化为弹簧-阻尼-质量模型。假定质量块在x方向受到某种激励作用而受迫振动，z轴有角速度Ω输入时，质量块在y方向就会受到交变的哥氏力作用而沿y轴方向产生诱发振动，由于哥氏效应产生的力为F=2mΩv(其中：v为质点相对于动系的径向速度或轴向速度矢量)，因而检测y方向的位移就可以解算出角速度[6]。

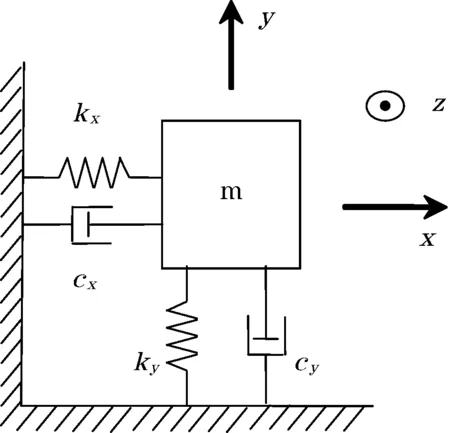
图1 振动陀螺的简化模型

设质量块m在x轴上受外部频率为ωc的简谐驱动力F=fxsin(ωct)作用，z轴方向输入角速度为Ω，陀螺在x方向和y方向的运动可以用下述动力学方程描述：

(1)

(2)

(3)

式中：cx、cy为各方向的阻尼系数；kx，ky为各方向的弹性系数；ωc、Qc为驱动方向(x轴)的谐振频率和品质因数；ωo、Qo为检测方向(y轴)的谐振频率和品质因数。

由式(1)可得到驱动模态的稳定解为

x(t)=xocos(ωct-φd)

(4)

式中：xo为驱动方向的幅值；φd为位移的相位角。

y(t)=Asin(ωct+φ)

(5)

(6)

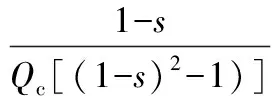
(7)

由式(5)、式(6)、式(7)可知，陀螺的稳态输出信号与驱动信号同频率。当驱动幅值xo、驱动方向品质因数Qc及谐振频率ωc与ωo为定值时，输出的简谐信号幅值正比于输入角速度Ω．因此，输入角速度可由解调得到的输出信号的幅值确定，这就是振动陀螺检测角速度的基本原理[6-7]。

1.2全对称振动陀螺的结构设计

全对称振动陀螺采用完全对称分布的4条导向横梁组成的全对称结构，结构的几何中心为垂直的惯性质量柱，外框架为口字形。该结构对称，并且中心质量柱惯性质量大，利于放大振动信号，增大哥氏力和振幅从而增加陀螺的灵敏度。文中结合陀螺的振动结构特点，采用压电驱动、压电检测的工作方式。这种工作方式产生的驱动力大，能够获得较高的位移分辨率和控制精度[8],并且结构简单，容易实现，充分利用压电片的正压电效应和逆压电效应。

对全对称振动陀螺进行结构设计时，需将体积大小控制在35 mm×35 mm×35 mm以内，购买的压电片长、宽、厚分别为8 mm、2 mm、0.2 mm．全对称振动陀螺的结构设计需以此为基础，结构设计见图2。陀螺横梁的长宽高尺寸:8.5 mm(l)×2.5 mm(w)×0.6mm(t)；中心质量柱尺寸：9 mm (h)×4 mm×4 mm。外框架为32 mm×32 mm，厚度为9 mm．

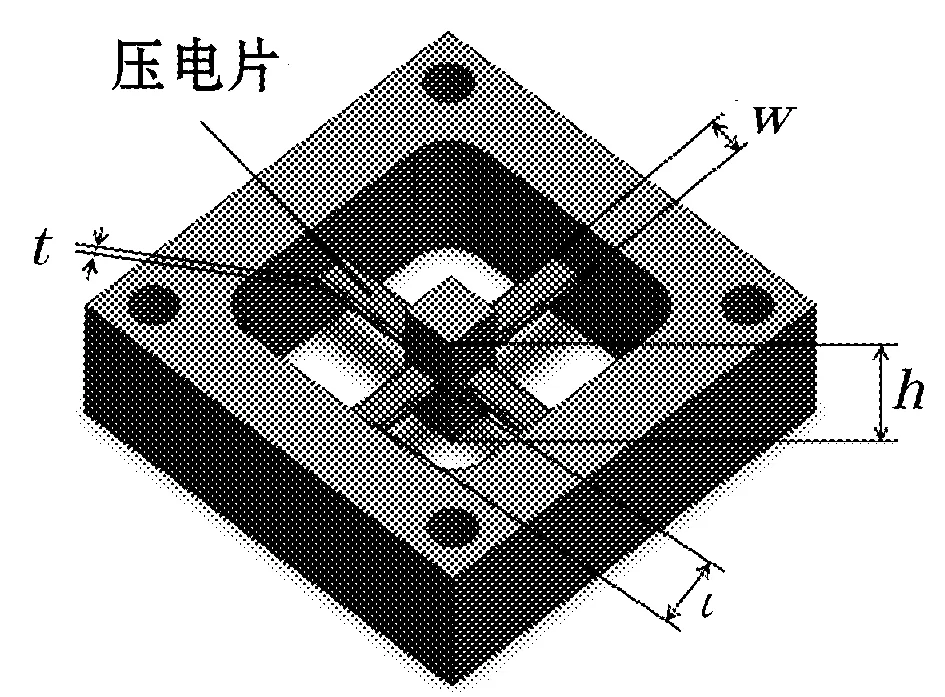
(a)陀螺结构尺寸示意图

(b)可测试的陀螺样机图2 全对称振动陀螺的结构设计

2 全对称振动陀螺的模态分析

要具有高性能指标，须在一定程度上增大陀螺检测模态的振动幅值以提高灵敏度。由式(3)、式(6)可以推导出：

(8)

式中：A为y方向的振幅，A与Ω的比值即为陀螺灵敏度。

要增大灵敏度就必须减小驱动方向x轴的阻尼系数，增大惯性质量来提高品质因数Q，并且使驱动模态与检测模态的谐振频率尽量接近，即实现模态匹配(ωc趋近于ωo，使s趋于0)[7],如果陀螺是理想状态，没有制作误差，那么由于对称性，陀螺的驱动模态与检测模态的谐振频率是一样的。

陀螺处于工作状态时还须抵抗外界振动干扰，并且避开陀螺自身可能产生的有害振动，有害振动会造成能量损失，不利于哥氏力的检测。这使得设计上需满足陀螺的固有频率要高于一般的外界振动频率(2 kHz左右)，同时陀螺的驱动模态和检测模态要尽量远离临近的有害振动模态[9]。

利用ANSYS WORKBENCH对初步设计的全对称振动陀螺进行模态分析。全对称振动陀螺采用了2种材料：陀螺零件结构为不锈钢；压电陶瓷片为掺铌的锆钛酸铅(PZT-5)。不锈钢和压电陶瓷片(PZT-5)的材料特性如表1所示。

表1 不锈钢和压电陶瓷片材料特性表

为保证压电片PZT-5与全对称振动横梁的重合部分传递力和位移的连续性，要采用黏结处理[10],使2个模型之间不存在相对滑动，并在陀螺零件的外框架的4个螺钉孔处施加3个方向的位移约束，尽量使模拟仿真接近真实环境。有限元模型见图3。3种对压电片处理类型相应的各阶模态频率如表2所示。

图3 全对称振动陀螺的有限元模型

表2 3种对压电片处理类型相应的各阶模态频率 Hz

其中贴上8片压电片的陀螺二阶、三阶模态仿真结果如图4所示。结合表2，陀螺的驱动(二阶)模态频率和检测(三阶)模态频率均9 185.7 Hz，与其他有害振动模态相距较远，降低了其他振动模态(主要是一阶和四阶模态)对陀螺造成的误差影响。各阶模态频率均高于一般的环境噪声频率，有抗振动性能。但频率超过9 000 Hz，导致高频电路过于复杂，会带来其他附加问题，有待优化。

(a)陀螺的驱动模态(二阶)

(b)陀螺的检测模态(三阶) 图4 陀螺的二阶、三阶模态仿真示意图

3 陀螺的结构参数优化

3.1 陀螺的结构参数对模态频率影响的分析

要确保陀螺驱动、检测模态远离其他有害振动模态，并处于抗振动的因素考虑，所有振动模态的频率都要高于某一阈值，就应先了解决定结构谐振频率的主要影响因素。通过Rayleigh(瑞利)能量法对陀螺谐振频率分析可以得到确定陀螺机械结构各阶振动模态的谐振频率的表达式：

(9)

式中：ki为支撑系统沿方向i的刚度系数;mi为被横梁带动的运动部分的等效质量[11]。

当全对称振动结构处于上下振动模态时，支撑系统可以认为由4根导向横梁组成。等效的刚度系数可以表示为

(10)

式中：E为材料的杨氏模量;l、w、t分别为全对称横梁的长度、宽度和厚度。

当全对称振动结构处于其他模态谐振状态时，振动更复杂，但ki和mi也仅与结构材料和尺寸有关。由此可知，陀螺各阶模态的谐振频率主要取决于陀螺横梁在各个方向的刚度系数及被横梁所带动部分的等效质量大小，这2项参数都由陀螺的结构材料和尺寸决定。因此，当材料一定时，可以通过改变陀螺的结构尺寸达到模态匹配的效果。

结合上述分析，利用ANSYS WORKBENCH进行模态分析，得到陀螺主要结构参数对各阶模态频率的影响规律。

3.2 压电片对模态频率的影响

由表2可知，压电片数量对陀螺模态频率的影响很大。压电片可以看作横梁的一部分，增强了横梁刚度，使模态频率增大。这也与实际情况更加接近，在之后的仿真都考虑8片压电片的情况，并将压电片作黏结处理以模拟真实环境。

3.3 横梁结构参数对模态频率的影响

陀螺结构最重要的一部分就是全对称振动横梁结构，合理的结构参数对于减小振动能量损耗、提高陀螺品质因数具有重要意义。采用单变量分析的方法，采用有限元方法，分析横梁结构参数对陀螺模态谐振频率的影响。

3.3.1 横梁长度的影响

模态频率与横梁的长度的关系，见图5。全对称振动陀螺的各阶谐振频率都随着横梁长度的增长而不断减小。在横梁的长度增大至9.5 mm时，一阶模态频率趋于2 kHz，随着横梁长度的继续增大，一阶频率将降至2 kHz以下，出于抗振考虑，横梁长度不能继续增长。

图5 横梁长度l对模态频率f的影响

3.3.2 横梁宽度的影响

模态频率f与横梁宽度w的关系，见图6。随着宽度w的逐渐变大，横梁的刚度系数增大，各阶模态的谐振频率增大。在二阶模态的谐振频率超过7 kHz时，驱动陀螺所需的高频电路过于复杂，所以横梁宽度不能过大。

图6 横梁宽度w对模态频率f的影响

3.3.3 横梁厚度的影响

模态频率f与横梁厚度t的关系，见图7。随着横梁厚度的增加，刚度系数不断增大，使得各阶模态谐振频率逐渐增大，二阶模态频率增长较快。在厚度为1 mm时，二阶模态频率达到12 kHz，会带来高频问题；厚度为0.2 mm时，一阶模态频率小于2 kHz，不可取。

图7 横梁厚度t对模态频率f的影响

3.4 中心质量柱质量大小对模态频率的影响

质量柱横截面保持不变的情况下，改变质量柱高度来改变惯性质量的大小，质量柱高度h对模态频率f的影响见图8。

图8 中心质量柱高度对模态频率f的影响

当质量柱高度增大，全对称振动结构的惯性质量将增大，模态频率将逐渐减小。质量柱高度太大、过小均不可取：高度太大，一阶模态频率趋近于2 kHz，二阶工作模态也与一阶模态相隔较近，容易受干扰；高度太小，会带来高频问题，同时减小惯性质量，降低灵敏度。

3.5 结构参数优化的结果

通过分析全对称振动横梁的结构参数对陀螺各阶模态频率的影响可知，陀螺的二阶和三阶频率必须高于2 kHz，但是又不能太高，频率如果过高，高频电路将过于复杂，结合陀螺的工作模态需求，以及加工便利可行的原则，最终采用粘贴8片压电片，设定全对称振动横梁结构参数：9 mm×2 mm×0.5 m，中心质量柱结构参数为：4 mm×4 mm×10 mm．

对优化后的陀螺进行有限元模态分析，3种对压电片处理类型相应的各阶模态频率见表3。其中贴上8片压电片的陀螺的二阶、三阶模态仿真结果见图9。从仿真结果中可以看出，在优化后陀螺的驱动(二阶)模态和检测(三阶)模态频率相等，均为5 699.9 Hz，与其他有害振动模态相距较远，有效降低其他振动模态(主要是一阶模态和四阶模态)对陀螺造成的误差影响。而且与优化前的9 185.7 Hz相比，解决了高频问题，频率又高于2 kHz，有抗振动性能，整体性能得到了优化，结构设计符合要求。

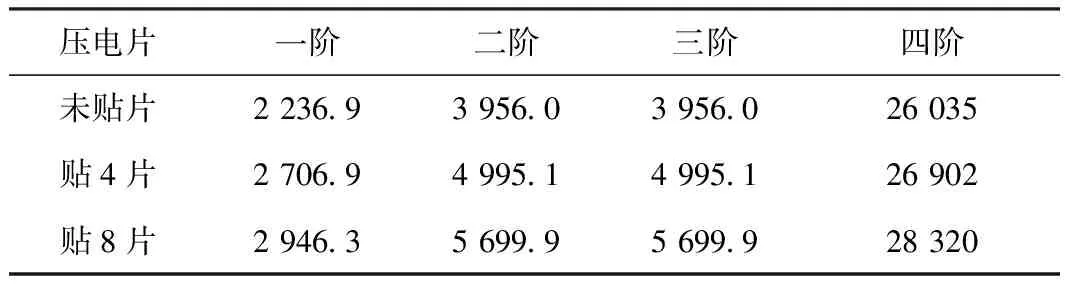
表3 3种对压电片处理类型相应的各阶模态频率(优化后) Hz

(a)陀螺的驱动模态(二阶)

(b)陀螺的检测模态(三阶)图9 优化陀螺的二阶、三阶模态仿真示意图

4 全对称振动陀螺仪样机制作和试验验证

按照优化后的结构尺寸对样机进行制作，组装好的陀螺样机如图10所示。对样机进行模态测试，通过测试得到了全对称振动陀螺样机的驱动和检测模态的谐振频率分别为5 905.7 Hz、6 024.0 Hz，频率差值为118.3 Hz，频率匹配系数为2.0%，测试得到的模态频率与仿真分析得到的结果也

有一定偏差。主要是由于陀螺在加工过程中的误差、应力变形以及压电片组装过程中的误差。这些误差导致陀螺质量不均、横梁结构不对称及2个方向阻尼系数不一致等，从而使2个模态频率不一致。但是，试验初步验证了这种振动陀螺的工作原理和结构设计的可行性。

图10 全对称振动陀螺

5 结束语

文中建立了全对称振动陀螺整体的结构设计模型，对陀螺模态进行了有限元分析，完成了陀螺的结构参数优化，并进行了样机制作和试验验证，由此可以得出以下结论：

(1)陀螺的结构参数对各阶模态的谐振频率有重要影响，当材料一定时，可以通过改变陀螺的结构参数达到模态匹配的效果。优化后横梁结构参数：9 mm×2 mm×0.5 m，中心质量柱结构参数为：4 mm×4 mm×10 mm，陀螺的驱动模态和检测模态频率相等，为5 699.9 Hz，整体性能得到了优化。

(2)对优化后的模型进行了样机制作和模态测试，得到了全对称振动陀螺样机的驱动和检测模态的谐振频率，有一定偏差，主要是制作误差导致。初步验证了这种振动陀螺的工作原理和结构设计的合理性和可行性。

参考文献：

[1] ANSARI M,ESMAILZADEH E,JALILI N.Coupled vibration and parameter sensitivity analysis of rocking-mass vibrating gyroscopes.Journal of Sound and Vibration,2009，327(3-5):564-583.

[2] BAE S Y,HAYWONH K J,YEE K Y,et al.High performance MEMS Micro-gyroscope.Conference on Design,Test,Integration,and Packaging of MEMS/MOEMS,Cannes-Mandelieu,2002:316-323.

[3] CHALLONER A D.Isolated resonator gyroscope:US,US6629460B2．2003-10-07.

[4] 王利强,宋菲君,任文杰.陀螺的分类、原理及应用现状.电子测量与仪器学报,2004(增刊):857-863.

[5] 谷庆红.微机械陀螺仪的研究现状.中国惯性技术学报,2003,11(5):67-72.

[6] 谢立强,吴学忠,李圣怡.音叉式石英微机械陀螺的驱动检测技术研究.国防科技大学学报,2005,29(1) :131-134.

[7] 何胜,王巍.MEMS振动陀螺驱动模态稳幅特性与控制.中国惯性技术学报,2009,17(4):469-473.

[8] 乔绪维,辛洪兵.微机械传动技术概述.机械传动,2010,34(11):86-90.

[9] 李锦明.电容式微机械陀螺仪设计.北京:国防工业出版社,2006:16-52.

[10] 蒋青,刘宇.压电振动陀螺振动梁节点的有限元分析.压电与声光,2007,29(2):216-218.

[11] 姜德义,郑拯宇,李林,任松.压电陶瓷片耦合振动模态的ANSYS模拟分析.传感技术学报,2003(4):452-456.