基于快速Myriad滤波方法的地震数据去噪

岳碧波，彭真明

(电子科技大学光电信息学院，四川成都610054)

噪声压制是地震信号处理中永远不能回避的话题。例如，在地震反演[1]和地震数据时频分析[2]等地震方法技术应用中，高品质的地震数据是取得精确结果的根本保障。但是，实际采集到的地震数据不可避免地受到噪声的污染，而且噪声的统计分布是不可预测的。为了减小噪声的影响，提高地震数据的信噪比以及分辨率，人们研究并采取了很多的措施。例如，通过组合和多次覆盖技术提高采集数据的信噪比[3];进行反Q滤波补偿[4-5]等。但是，这些方法在去除噪声的过程中往往又引入了新的计算误差，造成数据品质下降，而得不到人们预期的结果。传统的基于Fourier变换的去噪方法[6]、分数阶Fourier变换去噪方法[7]，以及小波变换滤波去噪方法[8]等等，是在频率域或者波数空间分解的信号处理技术，它们都默认了噪声是服从高斯分布的。这样做不仅是因为高斯分布概率密度函数简单，便于理论推导和分析，也因为高斯分布的频谱以及高阶谱很容易估计，从而使问题得到了很大的简化。实际上，地震数据中的噪声的统计分布是具不可预测性的，而且比高斯分布要复杂得多，尤其是噪声中往往含有的脉冲特性是高斯分布所不能描述的。

α稳定分布是一类在信号处理领域广泛应用[1,10-13]的统计分布，而且是目前唯一一种满足广义中心极限定理的分布[9]。该分布能够描述随机信号的非对称性以及脉冲特性等统计特性，更重要的是，当α稳定分布的特征参数取为2时，该分布退化为一般的高斯分布。因此，能够用高斯分布描述的统计特性，就一定能用α稳定分布来描述。这也是α稳定分布得到广泛重视的原因所在。

本文根据噪声中的脉冲特性，假设地震噪声是服从非高斯α稳定分布的，在此基础上采用一种改进的快速Myriad滤波方法[14]对含有脉冲噪声的理论模型数据和实际叠前地震资料进行去噪处理试验，并分别与经典的均值滤波和中值滤波方法进行对比，以证实快速Myriad滤波方法的技术优势和实用性。

1 Myriad滤波方法原理

Myriad滤波方法是针对α稳定分布提出的一种非高斯脉冲噪声滤波方法。在滤波过程中，采用滑动窗的方法，选取窗口中的数据参与计算，并将计算结果作为当前窗口滤波结果输出。Myriad滤波过程类似于均值滤波和中值滤波，但是，其针对脉冲噪声环境的滤波性能具有明显的技术优势。

1.1 基本Myriad滤波方法

假设X=[x1,x2,…,xN]T是一组包含有噪声的离散数据，数据的采样点数为N，Myriad滤波定义为[9-11]

(1)

式中:M为窗口长度;K是线性化参数。由(1)式可知，K值越大，则滤波器性能越接近于线性;K值越小，滤波器非线性特性越明显。实际滤波过程中，应根据噪声的脉冲特性强弱适当调整K。滤波器的运算是寻找一个β，使得窗口内的M级连乘式取得最小值，滤波器的输出YK就是寻找到的β。在基本Myriad方法的基础上，人们又提出了许多新的Myriad方法，例如加权Myriad方法[12]，FIR-Myriad方法[13]，等等。对(1)式进行直接求解存在一定的难度，限制了Myriad滤波方法的使用。

为了便于更加直观地了解Myriad滤波方法，以窗口长度M=5的Myriad滤波器为例予以解析。根据(1)式可以得到此时的Myriad滤波器表达式为

(2)

这里将滤波器的输出表示成了关于β的函数f(β)。由(2)式可见，当窗口长度M=5时，f(β)函数中自变量β的最高次数为10。显而易见，当滤波器窗口的长度为M时，滤波器中自变量β的最高次数将为2M;窗口选取得越长，β的最高次数越大。

用线性运算方法就可以求解(2)式的最小值。若取滤波器输出f(β)关于β的梯度f′(β)=0，求解该式理论上可得到一个β0，使得f(β0)=minf(β)。仍以窗口长度为M=5的滤波器为例，为便于求解，这里定义一个中间变量

(3)

这样(2)式可以表示为

(4)

(4)式两边对β求导，得到

(5)

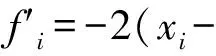
(6)

(6)式亦可表示为

(7)

在(7)式中，若K→∞，则(x2-β)2/K2→0，此时Myriad滤波器退化成线性的均值滤波形式

(8)

1.2 快速Myriad滤波方法

若以上述线性化的方法求解滤波器输出，会存在多解性的问题。仍以窗口长度M=5的滤波器为例，由(6)式或(7)式可见，该方程式的待求参数β的次数为9，直接求解将会得到9个解。一般地，若滤波器窗口长度为M，将会有2M-1个解。而滤波器每个窗口内只有一个值输出，多解的存在将会导致滑动窗口每次的输出值混乱。

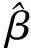
(9)

其中，

(10)

再定义一个变量

则(9)式可简化为

(11)

由(11)式，很容易解得

(12)

当窗口长度为M时，可以得到

(13)

相比于直接的梯度求解方法以及随机搜索方法，(13)式所示的快速Myriad滤波方法运算量小，而且稳定性高。在实际应用中，只要给定了窗口长度M和线性化参数K，直接使用(13)式便可得到窗口输出数据。

2 理论模型测试

用一组理论模型数据对快速Myriad滤波方法进行测试。该理论模型由多道含有加性随机噪声的合成地震数据构成。假设每道合成地震数据x由有用地震信号s和加性α稳定分布随机脉冲噪声n组成，即x=s+n。

α稳定分布是目前唯一的一类满足广义中心极限定理的分布，该分布相对于传统的高斯分布的优点在于，它能很好地描述带有脉冲特性的数据的统计特性。除了几种特殊情况外，α稳定分布没有确定的概率密度函数表达式，通常用特征函数来定义。α稳定分布的特征函数为[14]

(14)

其统计特性由4个参数决定，α∈(0,2]为特征指数，该参数取值越小，分布的拖尾越厚，即脉冲特性越强;β∈[-1,1]为对称参数;γ∈(0,+∞)为分散程度;μ为位置参数。特别地，当α=2，β=0时，α稳定分布退化为一般的高斯分布。

理论模型测试采用Chambers提出的方法产生一组α稳定分布随机噪声，各种方法的去噪效果用信噪比来衡量，信噪比SNR由下式定义

(15)

测试模型数据由30道含随机噪声的合成地震数据组成，数据采样率为1ms，采样点数为350。每道数据中的加性噪声均为服从参数α=1.85，β=0.2，γ=2.0和μ=0的非高斯α稳定分布随机数。不含随机噪声的合成地震数据及其加噪后的地震数据分别如图1a和图1b 所示。实际测得加噪后的地震数据的信噪比为-4.3257dB。由图1b 可见，噪声对有效信号的干扰很严重，噪声的最大脉冲幅值甚至超过了有效信号的最大振幅，除了最大波峰附近外，其它地方有效信号的波形基本上已经被噪声淹没。

为了通过比较来说明快速Myriad方法在脉冲噪声压制中的优势，对测试模型数据分别采用均值滤波方法、中值滤波方法和快速Myriad滤波方法进行去噪处理。均值滤波方法是一种线性的滤波方法，如前文所述，当线性化参数K→∞时，均值滤波器也可以看作是Myriad滤波的线性近似。中值滤波器是一种非线性滤波方法，对脉冲噪声有效;它与均值滤波器以及Myriad滤波具有类似的结构，先将滑动窗中的数据排序，然后选取中间值作为输出。为了便于比较，测试处理中3种方法的窗口长度均为M=5。

图2a为含噪模型数据(图1b)的均值滤波结果;图2b为滤除的噪声剖面，即图1b与图2a的差值剖面。由图2b可见，均值滤波器滤除的噪声幅值稳定，这表明滤波结果中仍有脉冲噪声没有被滤除，在图2a所示的滤波结果中可见明显的噪声也说明了这个问题。计算得出均值滤波后数据的信噪比为4.5534dB。

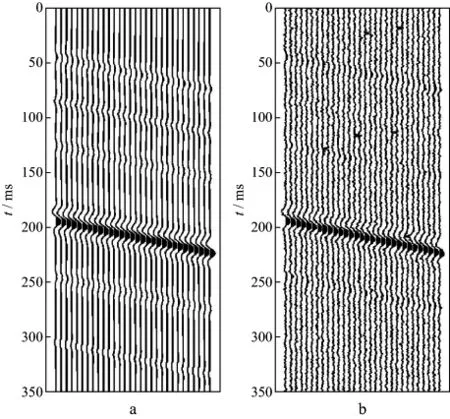
图1 理论模型合成地震数据(a)及其加噪后的结果(b)

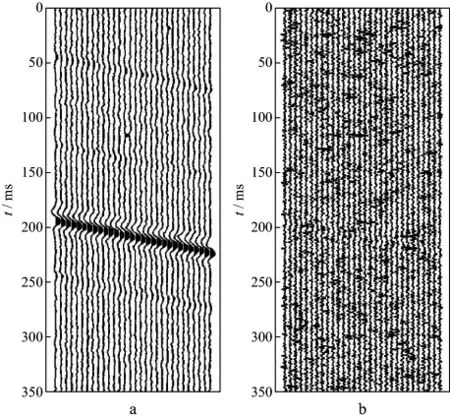
图2 理论模型合成数据的均值滤波结果(a)及滤除的噪声剖面(b)

图3a为含噪模型数据(图1b)的中值滤波结果;图3b为滤除的噪声剖面，即图1b与图3a的差值剖面。由图3a可见，虽然中值滤波能较有效地去除脉冲噪声，但同时对原信号波形损伤较大，在图3a中振幅较小的地方，波形的横向连续性已经变差。在图3b所示的噪声剖面中，存在大量的有用信号，表明中值滤波在滤除噪声的同时，将部分有用信号也误当成噪声一起滤除，造成信号损伤。实际计算得到中值滤波后数据的信噪比仅为0.7799dB。

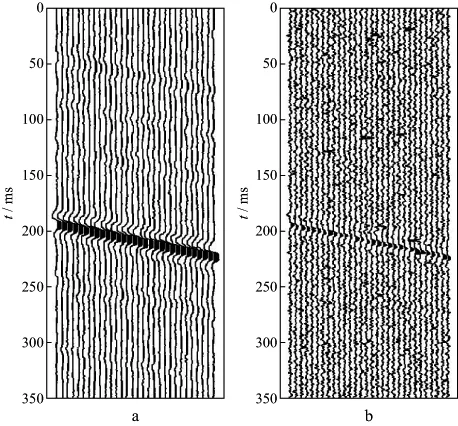
图3 理论模型合成数据的中值滤波结果(a)及滤除的噪声剖面(b)

图4a为含噪模型数据(图1b)的快速Myriad滤波结果，可见有用信号的波形基本上已完全恢复。图4b为滤除的噪声剖面，即图1b与图4a的差值剖面，可以看出含噪数据中的随机噪声几乎全部被清除，而且对原数据中的有用信号损伤很小。计算得到快速Myriad滤波后数据的信噪比为17.5204dB。

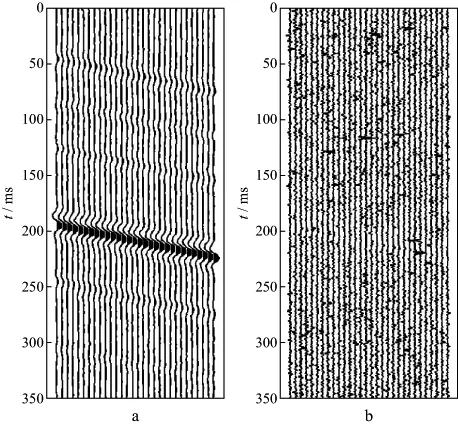
图4 理论模型合成数据的快速Myriad滤波结果(a)及滤除的噪声剖面(b)

通过图2a，图3a和图4a的对比分析可以得出结论，快速Myriad方法的滤波效果明显优于均值滤波方法及中值滤波方法。均值滤波器实际上是通过对数据做平滑处理而达到滤波的目的，当噪声中存在较大脉冲时，平滑方法就不一定能达到预期效果。因此，不难理解图2中经过均值滤波后的数据中仍含有明显脉冲噪声。而中值滤波则是通过对含噪信号在窗口内的排序、挑选，因此很容易将脉冲排除出去。但是其缺点也很明显，一是对从滑动窗口中挑选出的信号中的噪声没做任何处理;二是信号中的大幅度值也会被误当成噪声。所以，图3 中中值滤波后的数据不仅连续性仍很差，而且部分有用信号也被滤除。快速Myriad方法显然兼具了均值滤波和中值滤波所长，在滤除脉冲噪声的同时，也有效地保护了有用信息，而且滤波后数据的信噪比要远远高于均值滤波和中值滤波的结果。

3 实际地震数据去噪

将均值滤波、中值滤波和快速Myriad滤波3种方法分别应用到实际地震数据的去噪处理中，以验证快速Myriad滤波方法的实用性和有效性。3组滤波器窗口长度均为M=5。含有噪声的叠前地震数据剖面如图5所示，该剖面中共有120道地震数据，数据采样时间范围为1600～2400ms，采样率为2ms。由图5可见，叠前地震剖面上有3个强反射层，分别位于1600，1750，2100ms附近。

图5 实际叠前地震数据剖面

图6和图7分别是图5所示实际叠前地震数据的均值滤波和中值滤波结果。由于这两种方法本身性能上的局限性，实际地震数据中的3个强反射层对其滤波效果都产生了很大的影响。均值滤波将窗口内数据进行简单的求平均运算，当强反射响应的数据进入滤波窗口时，其很大的幅度值必然会对幅值较小的数据进行错误的修正;同理，幅值较小的数据也会将该幅值较大的数据平滑减小，从而进一步产生错误。而在中值滤波中，幅值较大的

数据甚至被直接排除。因此，在图6b和图7b的差值剖面中都可见这两种滤波方法在强反射层位置处对有效信号产生了较大的损伤。

图8a为经过快速Myriad方法滤波后的地震剖面(选取线性化参数K=0.5)，图8b为叠前地震数据与滤波结果的差值剖面，即滤波器所滤除的噪声。由图8a可见，经快速Myriad滤波后地震剖面上波形连续性增强，信噪比得到明显提高;而图8b中被滤除的噪声幅度平稳，且包含少许强脉冲，表明快速Myriad方法不仅滤除了叠前地震数据中分布较平稳的噪声(如高斯分布的白噪声)，同时也能将具有脉冲特性的噪声滤除。

图6 实际地震数据的均值滤波结果(a)及其差值剖面(b)

图7 实际地震数据的中值滤波结果(a)及其差值剖面(b)

图8 实际地震数据的快速Myriad滤波结果(a)及其差值剖面(b)

实际地震数据中的噪声分布是很复杂的，除了数据分布较平稳的高斯噪声外，不可避免的会含有脉冲噪声，所以，单一针对高斯噪声的滤波方法或专门针对脉冲噪声的滤波方法有时很难达到人们预期效果。快速Myriad滤波方法则能很好地解决这个问题，因为Myriad方法本身就是针对α稳定分布噪声提出的滤波方法，而α稳定分布是一类满足广义中心极限定理的统计分布，高斯分布只是其特例。理论模型测试和实际地震资料应用的结果表明，本文采用的快速Myriad滤波方法的实用性和有效性都明显强于经典的均值滤波方法和中值滤波方法。

4 结束语

实际地震数据中的噪声往往带有很强的脉冲特性，这些特性是传统的高斯分布函数所不能描述的，常用的基于高斯分布的滤波方法也很难达到理想的去噪效果。我们将一种非高斯噪声滤波方法——快速Myriad滤波方法应用到叠前地震数据去噪处理中。针对同一组包含脉冲随机噪声的理论模型数据的测试结果表明，快速Myriad滤波方法的滤波能力要远强于均值滤波和中值滤波方法。实际叠前地震数据的去噪处理结果中尖脉冲噪声被完全滤除，数据的信噪比得到明显增强，进一步证实了快速Myriad滤波方法在实际地震数据噪声滤除中的实用性和有效性。相信随着地震数据非高斯特性研究的不断深入，Myriad滤波等新的非高斯信号处理技术必将在地震数据处理中得到广泛的应用和发展。

参 考 文 献

[1] 岳碧波，彭真明，张启衡.基于α稳定分布的地震反演方法[J].地球物理学报，2012,55(4):1307-1317

Yue B B,Peng Z M,Zhang Q H.Seismic inversion method withα-stable distribution[J].Chinese Journal of Geophysics,2012,55(4):1307-1317

[2] 陈红，彭真明，王俊，等.地震信号Gabor变换谱分解方法及其应用[J].地球物理学报,2011,54(3):867-873

Chen H,Peng Z M,Wang J,et al.Spectral decomposition of seismic based on fractional Gabor transform and its application[J].Chinese Journal of Geophysics,2011,54(3):867-873

[3] 姜弢，林君，李桐林，等.相控震源对地震信号信噪比的改善研究[J].地球物理学报,2006,49(6):1819-1825

Jiang T,Lin J,Li T L,et al.Boosting signal to noise ration of seismic signals using the phased-array vibrator system[J].Chinese Journal of Geophysics,2006,49(6):1819-1825

[4] 姚振兴，高星，李维新.用于深度域地震剖面衰减与频散补偿的反Q滤波方法[J].地球物理学报,2003,46(2):229-233

Yao Z X,Gao X,Li W X.The forwardQmethod for compensation attenuation and frequency dispersion used in the seismic profile of depth domain[J].Chinese Journal of Geophysics,2003,46(2):229-233

[5] 严红勇，刘洋.用一种稳定的全反Q滤波方法提高叠前地震资料的分辨率[J].石油天然气学报，2011,33(6):59-63

Yan H Y,Liu Y.Improvement of pre-stack seismic resolution with stable full inverseQfiltering[J].Journal of Oil and Gas Technology,2011,33(6):59-63

[6] 张军华，吕宁，田连玉，等.地震资料去噪方法技术综合评述[J].地球物理学进展,2006,21(2):546-553

Zhang J H,Lv N,Tian L Y,et al.An overview of the methods and techniques for seismic data noise attenuation[J].Progress in Geophysics,2006,21(2):546-553

[7] 彭建亮,彭真明,张杰，等.基于分数域自适应滤波的地震信号去噪方法[J].地球物理学进展,2012,27(4):1730-1737

Peng J l,Peng Z M,Zhang J,et al.De-noising method of seismic signal based on adaptive filtering in fractional domain[J].Progress in Geophysics,2012,27(4):1730-1737

[8] 付燕.基于二次小波变换的地震信号去噪方法[J].石油地球物理勘探,2005,40(2):154-157

Fu Y.Noise-eliminated method for seismic signal based on second wavelet transform[J].Oil Geophysical Prospecting,2005,40(2):154-157

[9] Shao M,Nikias C L.Signal processing with fractional lower order moments:stable processes and their applications[J].Proceeding of the IEEE,1993,81(7):986-1010

[10] 张安清，邱天爽，章新华.α稳定分布的水声信号处理方法[J].电子与信息学报,2005,27(8):1201-1204

Zhang A Q,Qiu T S,Zhang X H.A new underwater acoustic signals processing approach toα-stable distribution[J].Journal of Electronics and Information Technology,2005,27(8):1201-1204

[11] Jia W,Kuruoglu E E,Zhou T.Alpha-stable channel capacity[J].IEEE Communication Letters,2011,15(10):1107-1109

[12] Tsakalides P,Nikias C L.The robust covariation-based music(roc-music) algorithm for bearing estimation in impulsive noise environments[J].IEEE Transactions on Signal Processing,1996,44(7):1623-1633

[13] Bates S,Mclaughlin S.The estimation of stable distribution parameters from teletraffic data[J].IEEE Transactions on Signal Processing,2000,48(3):865-870

[14] Bibo Y,Zhen M P,He Y M,et al.Impulsive noise suppression using fast Myriad filter in seismic signal processing[J].Expanded Abstracts of 5thInternational Conference on Computational and Information Science(ICCIS),2013,1001-1004

[15] Goh B M,Lim H S.Sequential algorithms for sample Myriad and weighted Myriad filter[J].IEEE Transactions on Signal Processing,2012,60(11):6047-6052

[16] Nubez R C,Gonzalez J G,Arce G R,et al.Fast and accurate computation of the Myriad filter via branch-and-bound search[J].IEEE Transactions on Signal Processing,2008,56(7):3340-3346

[17] Gonzalez J G,Arce G R.Optimality of the Myriad filter in practical impulsive noise environments[J].IEEE Transactions on Signal Processing,2001,49(2):438-441

[18] Kalluri S,Arce G R.Adaptive weighted Myriad filter algorithms for robust signal processing inα-stable noise environments[J].IEEE Transactions on Signal Processing,1998,46(2):322-334

[19] Lin B,Zhang C Y,Wang X D,et al.FIR-Myriad hybrid filters for signal processing in impulsive noise environments[J].First International Conference on Communications and Networking in China,2006,1-4