基于分形高频初始模型和低频先验信息的物性参数随机反演

印兴耀，孙瑞莹，张广智，王保丽

(中国石油大学(华东)地球科学与技术学院，山东青岛266580)

在勘探地球物理中，大尺度(低频)成分和小尺度(高频)成分都是储层和油藏描述的重要信息。地震数据的横向连续性好，但是具有带限性质；测井数据可提供钻孔附近的高分辨率的弹性参数和储层物性参数，但是缺乏区域覆盖。贝叶斯理论框架下的随机反演方法可以更好地融合地震数据和测井信息。常规的随机反演通常假定先验概率密度服从高斯分布，再利用测井数据建立变差函数来约束零空间。然而，服从高斯分布的假设有时是不恰当的，而且高斯分布仅由均值和方差表示。分形高斯概率密度函数由3个参数描述，即均值、方差和Hurst系数[1]。该方法可以产生高频的先验信息，并且基于分形理论产生的初始模型可以减少超出测井频带的假频出现[2]。基于分形理论的先验信息主要表征小尺度变化，大尺度的趋势可以由测井数据进行克里金插值并通过低通滤波得到，该初始模型常被用于确定性反演中，以获取地层趋势。这样，混合先验信息就包含了高频成分和低频成分。

储层物性参数是进行储层预测与流体识别的重要依据。基于地震反演得到的弹性参数，通过岩石物理模型估计储层物性参数，会存在不确定性传递，因此有必要开展物性参数的直接反演。而岩石物理是建立地震弹性参数和储层物性参数之间关系的桥梁，运用岩石物理理论可以进行岩石骨架和孔隙流体性质定性评价。Mukerji等[3-4]为了利用叠前AVO资料预测储层参数并对相应的不确定性进行评价，引入了统计岩石物理模型。随后Eidsvik等[5]、Spikes等[6]、Grana等[7-8]、胡华锋等[9]和夏丽娜等[10]也都进行了储层物性参数的反演研究。我们采用贝叶斯理论进行反演以获取后验概率密度的样本[11]，通过贝叶斯理论框架结合分形高斯模型算法、克里金插值、SA-PSO优化算法和统计岩石物理理论，克服了地震资料的带限性质，可以得到宽频带的反演结果。

1 方法原理

首先，基于分形理论得到高频初始模型，利用克里金插值得到低频初始模型，两者混合就是本文的初始先验实现；然后，利用SA-PSO优化算法进行优化，得到后验概率密度的样本。其中，优化算法中目标函数的建立包含了统计岩石物理理论。图1为基于分形高频初始模型和低频先验信息的储层物性参数随机反演流程。

图1 基于分形高频初始模型和低频先验信息的储层物性参数随机反演流程

1.1 岩石物理模型

岩石物理模型可以是测井曲线的简单回归拟合，也可以是更为复杂的物理模型。测井曲线的简单回归拟合一般不适用于整个工区，我们引入微分等效介质(DEM)模型和Gassmann方程，采用变化的孔隙纵横比逐点拟合测井曲线的方式来建立确定性岩石物理模型。首先，利用DEM解析模型和Gassmann方程建立岩石的纵、横波速度，密度与孔隙度,饱和度和矿物组分等各参数之间的关系;其次，将岩石孔隙等效为具有单一纵横比的理想椭球孔，应用非线性全局寻优算法来寻找最佳的等效孔隙纵横比，使得理论预测与实际测量的弹性模量之间的误差最小;最后，将反演得到的等效孔隙纵横比代入到Gassmann方程和DEM模型中构建纵波速度、横波速度和密度[12]。但是常规的确定性岩石物理模型都有一定的适用范围和局限性，因此我们在此基础上引入统计岩石物理模型。

统计岩石物理模型由确定性岩石物理模型和随机误差项构成，其中确定性岩石物理模型表征储层物性参数与弹性参数之间的岩石物理关系，随机误差项则用于弥补确定性岩石物理模型的局限性。统计岩石物理模型的数学表达式为

(1)

式中：m表示弹性参数体，m=[vP,vS,ρ];R代表储层物性参数，R=[φ,Vsh,Sw];vP,vS,ρ,φ,Vsh,Sw分别表示纵波速度、横波速度、密度、孔隙度、泥质含量和含水饱和度;fRPM(R)表示确定性岩石物理模型;ε为误差项，可以通过确定性岩石物理模型与实际测井资料之间的相对差异估算，通常取零均值截断高斯误差。

1.2 贝叶斯反演方法

AVO反演的理论基础是Zoeppritz方程及其近似式。我们提出的非线性反演方法在计算反射系数时，直接采用精确的Zoeppritz方程计算纵波反射系数，表达式为

(2)

式中：RPP表示P波反射系数;RPS表示S波反射系数;TPP表示P波透射系数;TPS表示S波透射系数;θ1和θ2分别为P波反射角和透射角;φ1和φ2分别为S波反射角和透射角;Δα，Δβ和Δρ分别表示界面两侧的纵、横波速度差及密度差，Δα=α2-α1，Δβ=β2-β1，Δρ=ρ2-ρ1;α，β和ρ分别表示纵波速度、横波速度及密度;下标1和2分别表示界面上、下两侧的参数信息。

假设地震褶积模型为

(3)

式中：d为观测地震数据;r为反射系数序列;e为服从高斯分布的随机噪声;G为子波褶积矩阵。可以建立反射系数序列r和反演的储层物性参数R之间的关系，即得到

(4)

根据贝叶斯理论可知[13]

(5)

式中：ρM(R)表示物性参数的先验信息(基于分形理论和克里金插值建立的先验模型);L(d/R)代表似然函数，表示模型与数据的匹配程度;k是概率归一化常数;σM(R)是贝叶斯后验分布。

1.3 先验信息建立

1.3.1 基于分形高斯模型的高频先验信息

测井资料分析表明，测井曲线的功率谱、变差函数和协方差通常呈幂律分布，幂指数为Hurst系数[14]。这样可以应用均值为0，具有特定自协方差结构的分形高斯分布来描述测井曲线形态[1]。自协方差函数为

(6)

式中：R是自协方差;σ是测井曲线的标准差;t是时间间隔;H是通过R/S分析方法求取的孔隙度、泥质含量和含水饱和度的Hurst系数[15]。

我们采用Srivastava等[1]的方法生成基于分形理论的高频初始模型。为了生成分形高斯模型，首先计算给定测井曲线的均值μ，方差σ2和Hurst系数H。然后利用公式(6)计算自协方差。根据维纳-辛钦定理，协方差函数的傅里叶变换是功率谱。该方法利用自协方差函数的傅里叶变换与和标准化的测井曲线同分布的随机数进行褶积，构建精确的分形高斯模型。

首先，由序列R，即R(0),R(1),…,R(M/2-1),R(M/2),R(M/2-1),…,R(1)的离散傅里叶变换计算精确的功率谱S(k)：

(7)

对于所有k，所有的功率谱S(k)≥0。

然后，产生均值为μ的独立同分布的高斯随机数W(k),k=0,1,…,M-1，利用测井数据的方差σ2进行标准化处理。

(8)

式中：“*”表示V(k)和V(M-k)是复共轭。

最后，用V(k)的离散傅里叶变换的前N个元素计算模拟序列Y(k)：

(9)

c=0,1,…,N-1

1.3.2 基于克里金插值的低频先验信息

克里金插值是在考虑了信息样品的几何特征和变量的空间结构信息后，为了达到线性无偏和最小估计方差的条件，对每个样品值赋予一定权值，利用加权平均值法对待估计区域的未知量进行估计的方法，也就是说是一种待定的滑动加权平均方法。图2为克里金估计示意图，即根据周围位置的数据来估计中间点位置的数值。以简单克里金为例，表达式可简要表示为

(10)

式中：C(ui,uj)表示采样点ui,uj间的协方差;C(uj,u0)表示未采样点u0与采样点uj之间的协方差;λi为待求的克里金系数。然后将其代入(11)式中，即可得到简单克里金的估计量和估计方差。

(11)

图2 克里金估计示意图解

1.3.3 混合初始模型建立

低频模型是通过测井数据进行克里金插值，然后进行低通滤波得到的。这个初始模型常用于确定性反演中获取地层趋势。在获得低频模型m1和基于分形理论的高频模型m2后，就可以进行简单的线性加权得到混合初始模型m：

(12)

式中：α为加权值，根据实际情况选取。如果原始测井曲线的储层参数变化较剧烈，可适当减小α;当储层参数变化较平缓时，可以适当增大α。如图3 和图4，由于选取的数据波动性不大，所以取α=0.7。

图3为分形初始模型反演结果与真实测井曲线的对比。图4为基于分形理论和克里金插值的混合初始模型反演结果与真实值的对比。由图3可以看出，基于分形理论初始模型的反演结果波动性较大，与真实值差异较大；而图4红色曲线所示的混合初始模型在一定程度上克服了抖动，更好地给出了曲线的趋势，与真实测井数据值更加接近。进行反演时，采用混合初始模型进行反演所需的计算时间更短，计算效率更高。

图3 分形初始模型与真实值的对比

图4 混合初始模型与真实值的对比

1.4 似然函数构建

本文方法的似然函数可表示为

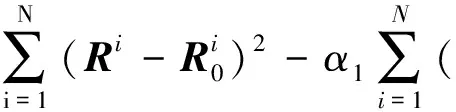
(13)

式中：s，μ，σ和H分别代表模拟地震波形的振幅、已知测井数据的物性参数的均值、标准差和Hurst系数;sobs，μobs，σobs和Hobs分别是观测地震数据、反演算法得到的物性参数的均值、标准差和Hurst系数;σ是期望数据不确定性的标准差;R代表反演的储层物性参数;R0是确定性反演中的低频约束信息;α，α1，α2和α3是可调参数，可通过不断测试得到所需的参数;s为由孔隙度、饱和度和泥质含量计算得到的合成记录，其中弹性参数和物性参数的关系由统计岩石物理模型确立。

(13)式似然函数中的第1项为反演算法中目标函数的基本结构(观测合成记录与反演合成记录差的L2范数)，第2项为确定性反演中常用的低频约束信息，第3，4，5项为基于分形理论的约束信息(均值、标准差和Hurst系数)。目标函数的后4项依赖于井资料，所以在离井近的位置，相应的权重可以取较大值;而远离井的位置，权重适当地减小。

1.5 SA-PSO混合优化算法

粒子群优化算法(Particle Swarm Optimization,PSO)是一种基于群体的随机优化算法，最先由美国学者Kennedy等[16]通过模拟鸟群觅食过程中的迁徙和群聚行为提出。粒子群优化算法通过个体之间的协作来寻找最优解。PSO中粒子向量的速度和位置变化公式为

(14)

式中：V为粒子i的速度向量更新;x为粒子i的位置更新;ω是惯性加权值，表示旧速度对新速度的影响;R1和R2为两个随机向量，是在[0,1]上均匀分布的随机数;c1和c2是学习因子;xpbest是粒子的局部最优位置;xgbest是粒子的全局最优位置。

然而，当粒子的飞行速度较大时，有利于全局搜索，但有可能飞过最优解;当粒子的飞行速度较小时，容易陷入局部最优[17]。鉴于以上缺陷，高鹰等[18]建议应用基于模拟退火的粒子群优化算法。该算法不仅基本保持了粒子群优化算法容易实现的特点，还改善了粒子群优化算法摆脱局部极值点的能力，提高了算法的收敛速度和精度。

模拟退火算法(Simulated Annealing,SA)的思想最早由Metropolis等[19]提出，Rothman[20-21]首先将模拟退火算法应用于地球物理问题。基于模拟退火改进的粒子群优化算法的(SA-PSO)流程如图5所示，其中SA选用快速模拟退火方法(Very Fast Simulated Annealing，VFSA)。

图5 SA-PSO优化算法流程

因此，首先根据分形理论和克里金插值得到具有高频和低频成分的初始模型，然后利用统计岩石物理模型建立弹性参数和物性参数之间的关系，最后依据SA-PSO优化算法进行优化，就可以得到后验概率密度的样本。

2 反演实例分析

2.1 一维数据测试

选取A井数据进行反演算法测试与分析。首先求取与A井相邻4口井的孔隙度、泥质含量以及含水饱和度的均值、方差和Hurst系数，从而建立基于分形高频模型和低频信息的混合初始模型(图4)，同时反演A井的孔隙度、泥质含量和含水饱和度，然后与真实数据值进行对比。图6是实际数据与基于分形高频初始模型和低频先验信息的储层物性参数反演方法得到的孔隙度、泥质含量和含水饱和度的对比结果，可以看出反演结果和真实测井曲线匹配得很好。

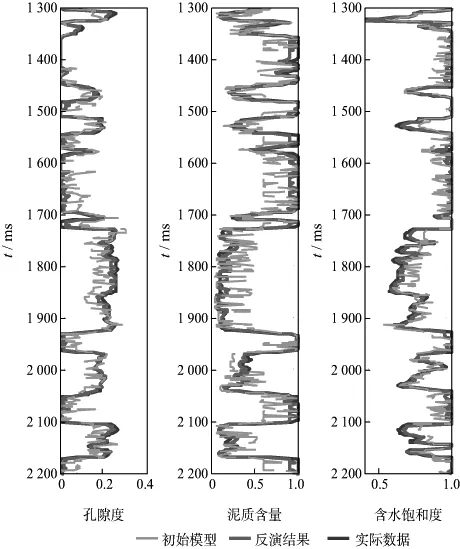
图6 反演结果与实际数据的对比

图7和图8分别是资料信噪比为4和1的反演结果，可以看出，只有部分层段与测井数据有一些差别，即使是在信噪比为1时，仍可很好地反演出储层物性参数的趋势，可以用于区分岩性和流体。通过加噪分析仍然可以得到可信的反演结果。

图7 资料信噪比为4时反演结果与实际数据的对比

图8 资料信噪比为1时反演结果与实际数据的对比

2.2 二维资料分析

二维地震资料来自于国内某油田实际工区。首先从该实际资料中提取正相位子波，然后对其进行基于分形高频初始模型和低频先验信息的储层物性参数随机反演。地震资料的纵向采样率为2ms，时间范围为1.10～1.30s，共有101道数据，图9显示的是叠后地震剖面。取该工区的5口井，基于除A井外的4口井进行分段交会分析，建立统计岩石物理模型和先验信息，用A井(盲井)验证反演方法的可行性。

图10，图11和图12分别是随机反演得到的孔隙度、泥质含量和含水饱和度，图中标示的曲线为A井的井曲线。可以看出，反演结果和A井的真实测井曲线匹配得很好，分辨率较高。对于孔隙度和泥质含量来说，即使是3.5m左右的薄层都可以分辨得比较清晰。由于测井解释的含水饱和度曲线分辨率稍差，所以反演结果的分辨率不是很高，但还是与解释的测井曲线吻合较好。该二维实际资料的应用结果验证了本文反演方法的可行性。

图9 叠后地震剖面

图10 反演的孔隙度剖面

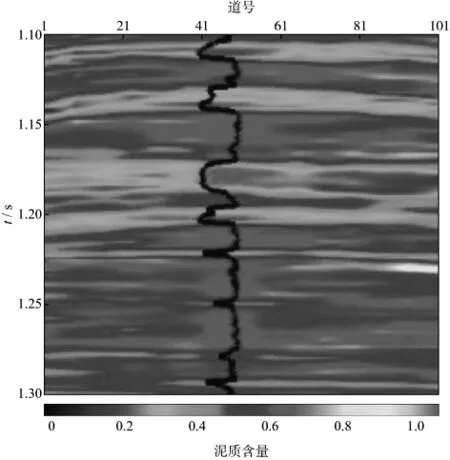
图11 反演的泥质含量剖面

图12 反演的含水饱和度剖面

3 结论与认识

我们引入统计岩石物理模型反演储层物性参数，弥补了确定性岩石物理模型的局限性。该反演方法直接采用精确的Zoeppritz方程计算正演合成地震记录，可以减少误差。基于分形方法产生的初始模型具有高频信息，同时可以减少假频的出现。克里金插值结果具有低频趋势，所以二者的混合初始模型同时具有高频和低频信息。利用基于模拟退火改进的粒子群优化算法进行优化，避免了粒子群优化算法易于陷入局部极值的缺点，提高了算法的精度和收敛速度。基于分形高频初始模型和低频先验信息的物性参数反演通过贝叶斯理论框架结合了分形高斯模型算法、克里金插值、SA-PSO优化算法和统计岩石物理理论。即使在信噪比相对较低时，仍然可以反演出合理的储层物性参数信息，从而为孔隙度、泥质含量以及含水饱和度的预测提供了一种可行的方法。

参 考 文 献

[1] Srivastava R P,Sen M K.Stochastic inversion of prestack seismic data using fractal-based initial models[J].Geophysics,2010,75(3): R47-R59

[2] Tao Y,Spikes K,Sen M K.Stochastic seismic inversion using both fractal and low-frequency priors[J].Expanded Abstracts of 81stAnnual Internat SEG Mtg,2011,2732-2735

[3] Mukerji T,Jørstad A,Avseth P,et al.Mapping lithofacies and pore-fluid probabilities in a North Sea reservoir:seismic inversions and statistical rock physics[J].Geophysics,2001,66(4):988-1001

[4] Mukerji T,Avseth P,Mavko G,et al.Statistical rock physics:combining rock physics,information theory,and geostatistics to reduce uncertainty in seismic reservoir characterization[J].The Leading Edge,2001,20(3):313-319

[5] Eidsvik J,Avseth P,Omre H,et al.Stochastic reservoir characterization using prestack seismic data[J].Geophysics,2004,69(4):978-993

[6] Spikes K,Mukerji T,Dvorkin J,et al.Probabilistic seismic inversion based on rock-physics models[J].Geophysics,2007,72(5):R87-R97

[7] Grana D,Della Rossa E.Probabilistic petrophysical-properties estimation integrating statistical rock physics with seismic inversion[J].Geophysics,2010,75(3):O21-O37

[8] Grana D,Dvorkin J.The link between seismic inversion,rock physics,and geostatistical simulations in seismic reservoir characterization studies[J].The Leading Edge,2011,30(1):54-61

[9] 胡华锋,印兴耀,吴国忱.基于贝叶斯分类的储层物性参数联合反演方法[J].石油物探,2012,51(3):225-232

Hu H F,Yin X Y,Wu G C.Joint inversion of petrophysical parameters based on Bayesian classification[J].Geophysical Prospecting for Petroleum,2012,51(3):225-232

[10] 夏丽娜.基于贝叶斯理论框架的储层参数地震反演方法研究[D].青岛:中国石油大学(华东),2013

Xia L N.The study of petro-physical properties seismic inversion based on Bayesian theory[D].Qingdao:China University of Petroleum (Huadong),2013

[11] Kjønsberg H,Hauge R,Kolbjørnsen O,et al.Bayesian Monte Carlo method for seismic predrill prospect assessment[J].Geophysics,2010,75(2):O9-O19

[12] 李宏兵,张佳佳,姚逢昌.岩石的等效孔隙纵横比反演及其应用[J].地球物理学报,2013,56(2):608-615

Li H B,Zhang J J,Yao F C.Inversion of effective pore aspect ratios for porous and its applications[J].Chinese Journal of Geophysics,2013,56(2):608-615

[13] Scales J A,Smith M L,Treitel S.Introductory geophysical inverse theory[M].Colorado:Samizdat Press,2001:1-193

[14] Hewett T A.Fractal distributions of reservoir heterogeneity and their influence on fluid transport[J].Expanded Abstracts of 61stSPE Annual Conference,1986,15386

[15] 韩忠玲.分形高斯噪声Hurst参数估计的实验评价[D].上海:华东师范大学,2008

Han Z L.Experimental evaluation on methods of the Hurst parameter estimation using fractional Gausssian noise[D].Shanghai:East China Normal University,2008

[16] Kennedy J,Eberhart R.Particle swarm optimization[C]∥Proceedings of IEEE international conference on neural networks.Neural Networks:Institute of Electrical and Electronics Engineers,1995:1942-1948

[17] 朱丽莉,杨志鹏,袁华.粒子群优化算法分析及研究进展[J].计算机工程与应用,2007,43(5):24-27.

Zhu L L,Yang Z P,Yuan H.Analysis and development of particle swarm optimization[J].Computer Engineering and Applications,2007,43(5):24-27

[18] 高鹰,谢胜利.基于模拟退火的粒子群优化算法[J].计算机工程与应用,2004,40(1):47-50

Gau Y,Xie S L.Particle swarm optimization algorithms based on simulated annealing[J].Computer Engineering and Applications,2004,40(1):47-50

[19] Metropolis N,Rosenbluth A,Rosenbluth M,et a1.Equation of state calculations by fast computing machines[J].The Journal of Chemical Physics,1953,21(6):1087-1092

[20] Rothman D H.Nonlinear inversion statistical mechanics and residual statics estimation[J].Geophysics,1985,50(12):2784-2796

[21] Rothman D H.Automatic estimation of large residual statics correction[J].Geophysics,1986,51(2):337-346