无网格点插值法大地电磁二维正演数值模拟

李俊杰，严家斌

(1.浙江省水利水电勘测设计院，浙江杭州310002;2.中南大学地球科学与信息物理学院，湖南长沙410083)

正演模拟是研究大地电磁的基础手段。当地下电性结构非一维时,大地电磁场响应没有解析表达式，必须借助正演数值模拟方法。作为大地电磁正演计算的常用网格方法，有限差分法(FDM)[1]、积分方程法(IEM)[2]及有限元法(FEM)[3-5]均有着各自的优缺点：有限差分法实现过程直接，但无法处理复杂地球物理模型;积分方程法只须对异常体进行剖分和求积，不涉及微分方法中的吸收边界等复杂问题，在三维电磁数值模拟研究中具有快速、方便等特点，但同样无法应对地下电阻率很复杂时的计算;有限元法适用于复杂物性分布和复杂边界形状的计算，其最大缺陷在于求解复杂模型时网格生成困难。

无网格法作为网格方法的重要补充和发展,是近十多年来兴起的一类数值计算新方法。其中，无单元Galerkin法(element-free Galerkin method，EFGM)[6]作为一种基于节点的无网格方法，已被成功用于地震波场[7-10]、雷达波场[11-12]及大地电磁场[13-15]响应的计算。相关文献的研究成果表明，EFGM具有较常规网格方法精度高、计算复杂模型便利的特性。然而，EFGM形函数不满足克罗内克δ函数性质(Ni(X)=δij)，边界条件加载较困难。无网格点插值法(MPIM)[16]是一种简单高效的无网格方法，较EFGM最大的改进在于形函数采用插值方法构造，边界条件可精确加载。此方法在弹性力学领域取得了很好的应用效果[16]，但在地球物理学领域的应用研究尚未见报导。

本文将无网格点插值法(MPIM)应用于大地电磁二维正演，介绍该方法的近似原理，推导大地电磁二维变分问题的无网格化离散过程;通过多个二维理论模型的MPIM，EFGM和FEM正演计算结果的对比，分析MPIM大地电磁二维正演数值模拟方法的特性和应用效果。

1 大地电磁二维变分问题

当地下电性结构为二维时，取走向为z轴，x轴与z轴垂直，y轴垂直向上；求解域Ω为矩形区域，4个顶点依次以A,B,C,D顺时针编号,Γ1为地质体的边界(图1)。

当平面电磁波以任何角度入射地面时，地下介质中的电磁波总是以平面波形式几乎垂直地向下传播，满足[17]:

图1 大地电磁二维正演求解区域a 电场极化模式(TE模式); b 磁场极化模式(TM模式)

(2)

对于TM模式:

(3)

式中:ω为角频率;μ为磁导率;σ为电导率;ε为介电常数。

2 大地电磁二维变分问题的无网格解法

MPIM利用位于积分点支持域内的场节点构造形函数，需用一组背景网格将求解区域离散以便建立离散系统方程，如图2所示。由于背景网格的积分常选用高斯积分法，故积分点又称高斯积分点或高斯点。

2.1 支持域

常用的支持域形状有圆形与矩形两种(图2)，

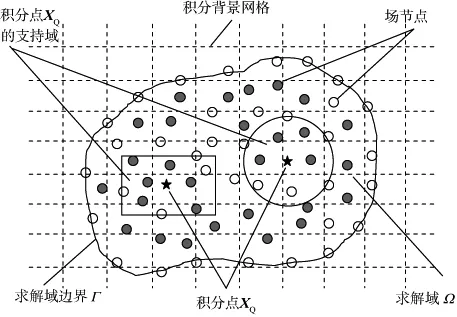
图2 无网格点插值法的背景网格、支持域、积分点与场节点

对于任一高斯点XQ，其支持域尺寸d由下式确定:

(4)

式中:α为支持域的无量纲尺寸，它用于控制实际支持域的大小，是对无网格法计算精度影响很大的一个参数[16]。dc为位于高斯点XQ附近的平均结点间距，可由下式确定：

(5)

式中:A为预估的支持域面积;n为包含在A中的节点数。对于节点均匀分布的情况，dc为节点间距。本文采用矩形支持域，故有两个方向的支持域尺寸，即

(6)

式中:dcx与dcy分别为横、纵向节点间距;αx与αy为对应的支持域无量纲尺寸。为便于程序设计，研究中常取αx=αy=α，本文取α=1.0。

2.2 点插值法近似

求解域Ω中任意一点X处的场变量u(X)的近似表达式为

(7)

式中:pT(X)为二维空间坐标XT=[xy]的基函数;a是系数向量;m为单项式的个数。p(X)可用Pascal三角形确定，对于一维(1D)和二维(2D)空间，其线性基函数分别为

pT(X)=1xm=2p=1

(1D)

pT(X)=[1xy]m=3p=1

(2D)

二次基函数分别为

pT(X)=[1xx2]m=3p=2

(1D)

pT(X)=[1xyx2xyy2]

m=6p=2

(2D)

完备的p阶多项式一般可由下式表示

基函数阶次的增加不能显著提高无网格法的近似精度，反而降低了计算效率[8]，一般取线性基即可。将(7)式写成矩阵的形式:

(8)

式中:U=[u1u2…un]T;a=[a1a2…an]T;P的展开式为

(9)

传统PIM中局部支持域内的节点数总是等于基函数个数(m=n),因此(9)式是一方阵的形式，系数向量a可通过矩阵的逆运算得到,即

(10)

将(10)式代回(7)式得

(11)

式中，ΦT(X)即为计算点X在支持域内的PIM形函数,其表达式为

ΦT(X)=pT(X)P-1=

[φ1(X)φ2(X) …φn(X)]

(12)

因为采用多项式基函数，PIM形函数的求导运算较容易，有

(13)

采用多项式作为基函数时，PIM插值形式简单，并且对于规则分布的场节点的插值具有较高的精度。此外PIM形函数满足克罗内克δ函数性质，因此边界条件加载较容易。

然而(9)式的求解是以P非奇异为前提的，当多项式基选用不合理或场节点分布不恰当时，P可能呈现高度病态甚至呈现奇异性，虽然存在随机移点法[16]、局部坐标变换法[18]等处理P奇异性的方法，但这些方法均或多或少存在不足之处，限制了多项式PIM的应用。

2.3 无网格离散系统方程的构造

定义了无网格形函数，便可以构造(1)式的离散系统方程，将变分符号代入(1)式有

(14)

u=[φ1φ2…φn][u1u2…un]T

(15)

式中:Φ为形函数矩阵;n为支持域内的节点数;u为支持域内n个节点的场向量。对(15)式进行变分运算有

(16)

将(16)式和(15)式代入(14)式，得

(17)

(17)式采用支持域内n个场节点编号。对于求解域内所有场节点,还应有一套总体编号体系，用于将局部节点矩阵组装成总体刚度矩阵。当节点I和节点J位于不同支持域时，其相应的被积函数为0，此时可得到按求解域节点编号的总体编号体系方程

(18)

(18)式可简写为

(19)

由于δUT是任意的，故(19)式成立的条件为

(20)

(20)式即为无网格点插值法构造的系统方程。

2.4 求解域背景网格积分

(20)式中的K包含对求解域Ω与求解域边界Γ的积分，为计算这些积分，须将求解域离散成一组背景网格(图2)，总体积分可表示成这些单元积分之和的形式，每个单元的积分利用高斯积分法求解,即

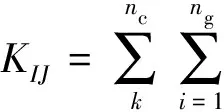
(21)

背景网格积分是MPIM中最重要的数值计算问题之一，总积分点数一般取支持域内场节点数量的2～8倍，但高斯点数目的增加并不能显著提高无网格法的计算精度，反而极大地降低了计算效率[15]，因此本文每个背景单元仅采用4(2×2)个高斯点，每个边界单元采用2个高斯点。求解线性方程组KU=0还需加载边界条件，可采用与FEM相同的罚函数法[16]加载。先将刚度矩阵中相应的对角元素KII变为αKII(α为惩罚系数，其值可取104～1010),然后用边界上的uI值取代方程组右端的零向量即可。

3 正演计算及效果分析

3.1 计算精度

图3 模型一

设计一个3层介质模型(模型一，图3)，验证MPIM计算大地电磁场响应的高精度特性。该模型第1层电阻率ρ1=500Ω·m,层厚h1=1km;第2层电阻率ρ2=2000Ω·m,层厚h2=3km;第3层电阻率ρ3=100Ω·m,层厚h3=4km。场节点等间距分布于问题域，对于TE模式，使用3321(41×81)个场节点，3200(40×80)个背景网格，横、纵向节点间距均为200m;对于TM模式，使用1681(41×41)个场节点，1600(40×40)个背景网格，节点间距与TE模式相同。分别采用EFGM，MPIM和FEM进行正演计算与对比，有限元法节点的分布与无网格法一致。

表1和表2分别为EFGM，MPIM和FEM计算的视电阻率及视相位数值相对误差。相对误差值的大小对应着数值方法计算精度的高低，相对误差值越大，精度越低，反之则精度越高。由表1可见,3种数值方法计算精度相当，且精度均随频率的增高而降低，精度变化范围约为3×10-10～4×10-3;当频率f<10-3Hz时，MPIM精度约高出EFGM一倍，大于此频点时MPIM精度与EFGM相当。视相位数值计算精度变化规律与视电阻率类似，精度约为2×10-10～4×10-4(表2)。

3.2 有效性

为了进一步说明MPIM求解MT问题的有效性，设计图4所示的二维模型(模型二):围岩电阻率ρ1=1000Ω·m，方形二度异常体电阻率ρ2=100Ω·m，方形截面边长L=400m，异常体顶部到地面的距离h=800m，场节点的分布与计算3层介质模型时相同(图4a)。分别采用EFGM，MPIM和FEM进行正演计算与对比，图5为频率f=100Hz时模型二的数值计算结果曲线，由图5可见，MPIM计算结果与EFGM和FEM基本一致，视电阻率曲线极小值与视相位曲线极大值的横坐标(X=0)正好对应于方形截面中心在地面的投影，证明了二维情况下MPIM的正确性。

图6为模型二的FEM，EFGM与MPIM视电阻率计算结果断面图，可见3种数值方法计算结果仍然一致且对称性良好。TE模式下，在100Hz频点附近，MPIM和EFGM与FEM断面图存在细微差异;TM模式下，形函数采用插值法构造的数值方法MPIM与FEM计算结果一致，较形函数采用拟合法构造的EFGM在10-4～10-3Hz低频段存在轻微差异。

表1 3层模型视电阻率数值解的相对误差

表2 3层模型视相位数值解的相对误差

图4 二维理论模型a 模型二; b 模型三; c 模型四; d 模型五

图5 频率f=100Hz时图模型二的数值计算结果a 视电阻率数值计算结果; b 视相位数值计算结果

3.3 计算效率

MPIM中模型参数的加载基于高斯积分点而非单元，高斯点的位置可由坐标确定，该特性使其在复杂地质模型构建上较常规网格方法方便。为表明MPIM的这一优势，采用与前文相同的节点分布计算了如图4b至图4d所示的二维模型:模型三为圆形截面低阻体，电阻率ρ2=100Ω·m，围岩电阻率ρ1=1000Ω·m，低阻体截面半径R=200m，异常体顶部到地面的距离h=800m;模型四与模型五为出露于地表的条带状低阻体，异常体截面呈平行四边形，下底长a=400m，上下底间距d=600m，异常体右边界与地面的夹角分别呈45°与30°，其电阻率及围岩电阻率与模型二相同。

图7为模型三的MPIM和EFGM视电阻率计算结果,由图7可见，TE模式异常横向拉长，TM模式异常纵向拉长，两种模式下数值计算结果均很好地反映了低阻异常体的存在。

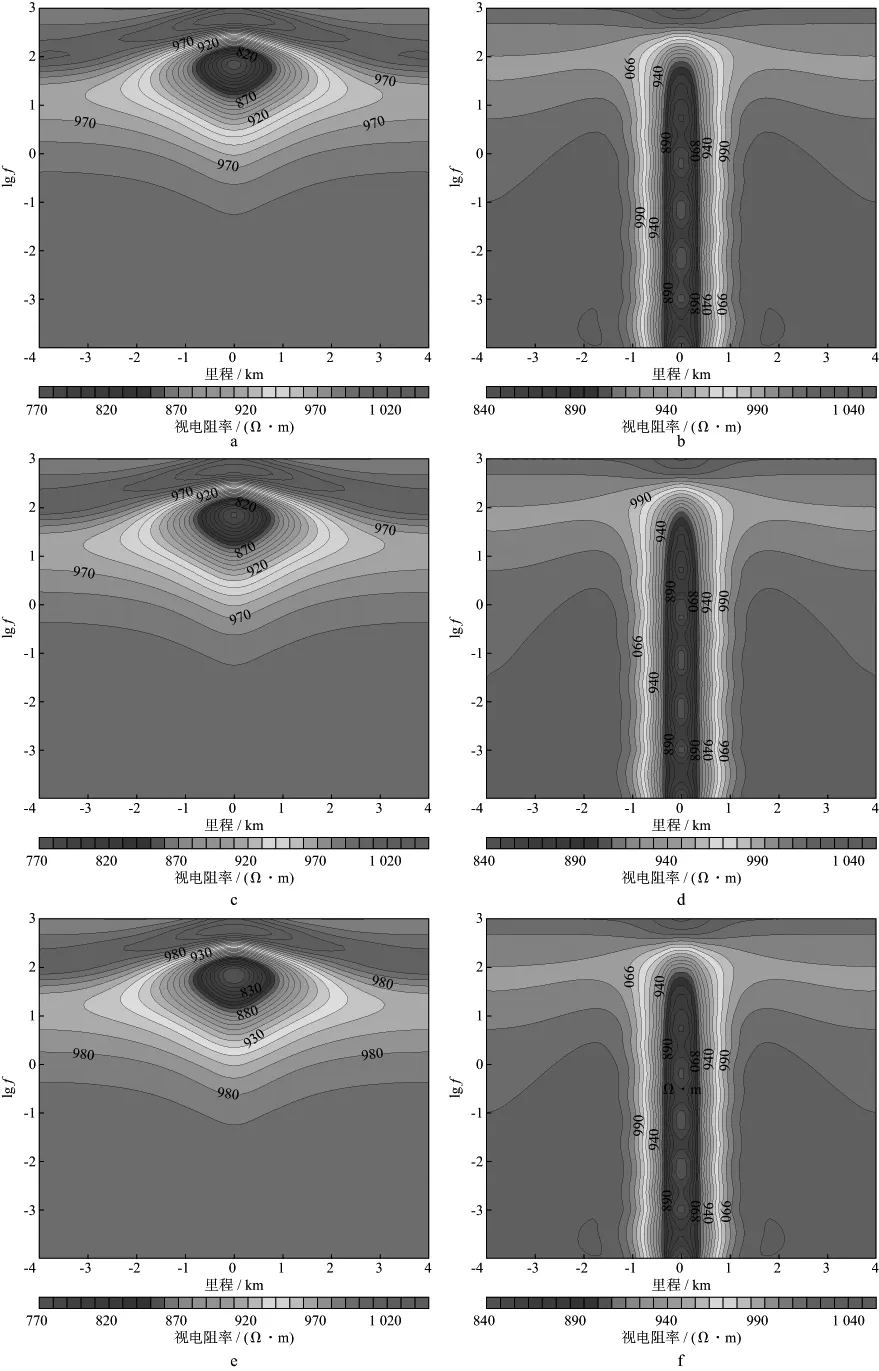
图6 模型二视电阻率数值计算结果a TE模式FEM视电阻率; b TM模式FEM视电阻率; c TE模式EFGM视电阻率; d TM模式EFGM视电阻率; e TE模式MPIM视电阻率; f TM模式MPIM视电阻率

图7 模型三视电阻率数值计算结果a TE模式EFGM视电阻率; b TM模式EFGM视电阻率; c TE模式MPIM视电阻率; d TM模式MPIM视电阻率

图8为模型四与模型五的TE模式MPIM和EFGM计算结果，横坐标为里程，纵坐标为以2为底的对数工作频率。由图8可见，①模型四与模型五的视电阻率断面呈现左右不对称，低阻区域呈“上窄下宽”状分布，模型四视电阻率变化范围均为100～1060Ω·m，异常特征显著;②低阻区域呈倾斜条带状分布，倾向与地质体的倾向相同;③模型五视电阻率变化范围均为100～1160Ω·m，其断面较模型四低阻条带呈现的倾角更大，且EFGM异常区断面较MPIM更为宽泛，如图8c和图8d 所示)。

以上模型试算分析可见EFGM和MPIM的高精度特性及其在计算复杂地质模型上的优越性。虽然无网格法与有限元法均达到精度要求，但在计算耗时上却存在较大差异,表3列出了3种数值算法计算模型二的耗时，工作频率为10-4～103Hz，共17个频点。由表3可见：①3种数值算法的计算速度由快到慢依次为FEM，MPIM，EFGM，EFGM计算耗时约为FEM的10倍;②MPIM速度较EFGM快，TM模式下效率提高8%，TE模式下提高5%。

无网格法(MPIM和EFGM)计算的耗时主要花费在形函数的构建及数值积分上[15]，计算效率的提升是无网格法广泛应用需解决的首要问题，无网格方法与高效网格方法的耦合或许可成为一个可行的方向。

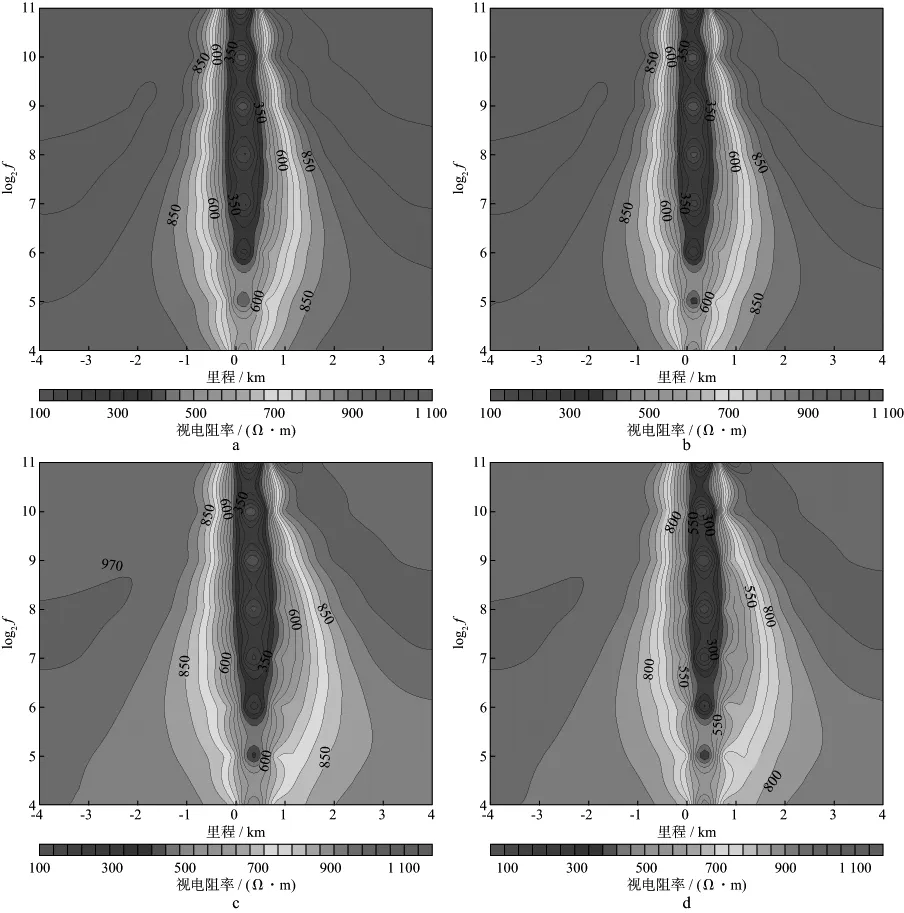
图8 TE模式模型四与模型五视电阻率无网格法计算结果a 模型四EFGM视电阻率计算结果; b模型四MPIM视电阻率计算结果; c 模型五EFGM视电阻率计算结果; d 模型五MPIM视电阻率计算结果

s

4 结束语

复杂地质模型电磁响应的计算一般需采用非结构化网格，此种网格的生成算法较复杂。本文将MPIM应用于大地电磁二维正演数值模拟，介绍了MPIM的基本原理及大地电磁二维变分问题的无网格化求解过程;采用节点规则分布的无网格法(MPIM和EFGM)计算出了柱形二度体及倾斜条带状二度体模型的电磁响应。理论模型的MPIM，EFGM和FEM正演计算结果的对比分析表明:MPIM适用于大地电磁正演计算，其计算精度很高，数值算例表明精度最高可达10-9数量级;MPIM与EFGM精度相当，但MPIM的计算效率更高，本文17个频点下的数值计算表明TM模式下效率提高8%，TE模式下提高5%。研究结果验证了MPIM大地电磁二维正演数值模拟方法的有效性，体现了MPIM在处理复杂地质模型正演问题上的优越性。

参 考 文 献

[1] 谭捍东，余钦范，Booker J，等.大地电磁法三维交错采样有限差分数值模拟[J].地球物理学报,2003,46(5):705-711

Tan H D,Yu Q F,Booker J,et al.Magnetotelluric three-dimensional modeling using the staggered-grid finite difference method[J].Chinese Journal of Geophysics (in Chinese),2003,46(5):705-711

[2] Wannamaker P E.Advances in three-dimensional magnetotelluric modeling using integral equations[J].Geophysics,1991,56(11):1716-1728

[3] Key K,Weiss C.Adaptive finite-element modeling using unstructured grids:the 2D magnetotelluric example[J].Geophysics,2006,71(6):291-299

[4] 刘长生,汤井田,任政勇,等.基于非结构化网格的三维大地电磁自适应矢量有限元模拟[J].中南大学学报(自然科学版),2010,41(5):1855-1859

Liu C S,Tang J T,Ren Z Y,et al.Three-dimension magnetotellurics modeling by adaptive edge finite-element using unstructured meshes[J].Journal of Central South University (Science and Technology),2010,41(5):1855-1859

[5] Ren Z Y,Tang J T.3D direct current resistivity modeling with unstructured mesh by adaptive finite-element method[J].Geophysics,2010,75(1):7-17

[6] Belytschko T,Lu Y Y,Gu L.Element-free Galerkin methods[J].International Journal for Numerical Methods in Engineering,1994,37(2),229-256

[7] 贾晓峰,胡天跃.滑动最小二乘法求解地震波波动方程[J].地球物理学进展，2005，20(4):920-924

Jia X F,Hu T Y.Solving seismic wave equation by moving least squares (MLS) method[J].Progress in Geophysics,2005,20(4):920-924

[8] 贾晓峰,胡天跃,王润秋.复杂介质中地震波模拟的无单元法[J].石油地球物理勘探,2006,41(1):43-48

Jia X F,Hu T Y,Wang R Q.A mesh-free algorithm of seismic wave simulation in complex medium[J].Oil Geophysical Prospecting,2006,41(1):43-48

[9] 贾晓峰,胡天跃,王润秋.无单元法用于地震波波动方程模拟与成像[J].地球物理学进展，2006，21(1):11-17

Jia X F,Hu T Y,Wang R Q.Wave equation model-

ing and imaging by using element-free method[J].Progress in Geophysics,2006，21(1):11-17

[10] 王月英.地震波正演模拟中无单元Galerkin法初探[J].地球物理学进展,2007,22(5):1539-1544

Wang Y Y.Study of element-free Galerkin method in the seismic forward modeling[J].Progress in Geophysics,2007,22(5):1539-1544

[11] 冯德山,王洪华,戴前伟.基于无单元Galerkin法探地雷达正演模拟[J].地球物理学报,2013,56(1):298-308

Feng D S,Wang H H,Dai Q W.Forward simulation of ground penetrating radar based on the element-free Galerkin method[J].Chinese Journal of Geophysics,2013,56(1):298-308

[12] 戴前伟,王洪华.基于随机介质模型的GPR无单元法正演模拟[J].中国有色金属学报，2013,23(9):1-9

Dai Q W,Wang H H.Element free method forward modeling of GPR based on random medium model[J].The Chinese Journal of Nonferrous Metals,2013,23(9):1-9

[13] 苏洲,胡文宝,朱毅.二维大地电磁正演中无网格算法研究[J].石油天然气学报,2012,34(5):87-90

Su Z,Hu W B,Zhu Y.Meshfree method used in two-dimensional magnetotelluric forwarding[J].Journal of Oil and Gas Technology,2012,34(5):87-90

[14] 李俊杰,严家斌.无网格法进展及其在地球物理学中的应用[J].地球物理学进展,2014,29(1):452-461

Li J J,Yan J B.Developments of meshless method and applications in geophysics[J].Progress in Geophysics(in Chinese),2014,29(1):452-461

[15] 李俊杰.基于弱式无网格法的大地电磁二维正演[D].长沙:中南大学地球科学与信息物理学院,2014

Li J J.Magnetotelluric two-dimensional forward by weak-form meshfree methods[D].Changsha:Central South University of Geosciences and Info-Physics (in Chinese),2014

[16] Liu G R,Gu Y T.A point interpolation method for two-dimensional solids[J].International Journal for Numerical Methods in Engineering,2001,50(4):937-951

[17] 徐世浙.地球物理中的有限单元法[M].北京:科学出版社，1994:229-235

Xu S Z.Finite element method for geophysics[M].Beijing:Science Press,1994:229-235

[18] Liu G R.Meshfree methods:moving beyong the finite element method[M].USA:CRC Press,2002:123-126