含倾斜裂隙页岩介质地震波场传播特征研究

周进举,王德利,靳 松,冯 飞

(1.吉林大学地球探测科学与技术学院，吉林长春130026;2.中国石油大学(北京)物探重点实验室，北京102249)

页岩作为一种典型的横向各向同性介质，不同于传统的地震勘探中各向同性的地震模型，在地震勘探中必须考虑其各向异性的特点，建立相应的地质模型。另外，在实际地质条件下，页岩中常常含有垂直或倾斜裂隙，而裂隙受多种因素控制，有很明显的各向异性特征，同时裂隙也是页岩气储存的重要空间和运移的重要通道[1]。因此，若对页岩气储层的地质条件进行模拟，我们应当考虑含有裂隙的各向异性模型，而研究的基础就是获得各种裂隙各向异性等效模型的弹性参数。

对于含裂隙介质弹性系数的计算，Hudson[2-4]提出了微裂隙理论，用这个理论可以计算出广泛扩容性各向异性(Extensive Dilatancy Anisotropy，简称EDA)介质的弹性常数;Schoenberg等[5-6]提出的线性滑动理论解决了方位各向异性介质和含垂直裂隙横向各向同性介质的等效弹性系数的计算问题;2002年，傅旦丹等[7]根据Backus方法并结合Hudson微裂隙理论，推出了周期性薄互层(Periodic Thin Layer，简称PTL)与EDA组合等效正交各向异性介质弹性常数的计算公式;同年，王德利等[8]根据Hudson等关于裂隙介质弹性系数计算的扰动理论和Bond变换矩阵原理，计算了含两组斜交的垂直裂隙形成的单斜各向异性介质的等效弹性系数。

对于含垂直裂隙的页岩介质，可以建立PTL与EDA的组合模型，这种组合模型在长波长情况下已经证明具有正交各向异性的性质;同样，当裂隙倾斜时，可以建立一个PTL+倾斜EDA模型，在长波长情况下，即波长远大于薄互层层厚时，这种介质是否具有倾斜横向各向同性(TTI)介质的性质就成了值得研究的问题。目前，国内外针对TTI介质的正演模拟做了很多研究工作。吴国忱等[9]作了TTI介质弹性波频率-空间域有限差分模拟，并分析了TTI介质弹性系数变化时的波形变化规律。祝贺君等[10]用高阶同位网格有限差分法对TTI介质地震波场进行了模拟;Saenger等[11]用旋转网格有限差分法对各向异性介质进行了正演模拟;Han等[12]对倾斜横向各向同性介质进行了弹性波模拟。以上的研究都是直接旋转VTI介质弹性系数得到TTI介质弹性系数，然后进行正演模拟，他们的模拟结果可以作为对照，来证明PTL+倾斜EDA模型是否具有TTI各向异性特征。

本文在前人对含裂隙介质弹性系数计算的研究基础上，针对PTL+倾斜EDA组合模型，利用Hudson理论计算出每层EDA介质的弹性系数，然后通过Bond变换得到倾斜EDA介质的弹性系数，在长波长的情况下，用Backus加权平均法计算了整体的等效弹性系数。进而用高阶旋转网格有限差分法对该模型的地震波场响应进行了正演模拟，证明了所给出的含倾斜裂隙页岩介质弹性系数计算方法的正确性。模拟结果与TTI介质的模拟结果相对照，证明了PTL+倾斜EDA组合模型，即含倾斜裂隙页岩介质，具有和TTI介质类似的各向异性特征。另外，这种方法还可以用于研究含倾斜裂隙薄互层介质中裂隙倾角、裂隙密度和裂隙填充物性质对地震波传播的影响。

1 弹性系数的计算

页岩介质是典型的PTL介质，在PTL模型中加入倾斜裂隙，即可很好地模拟含倾斜裂隙页岩介质。我们把这种模型称为PTL+倾斜EDA介质，如图1所示。

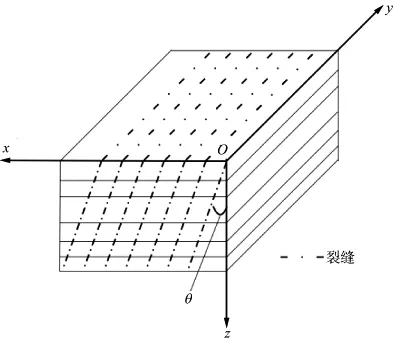
图1 PTL+倾斜EDA介质

对于PTL介质的每一层都可以看作是倾斜的EDA介质，则每一层的弹性系数都可以用计算EDA介质的方法求得，然后再进行Bond变换，倾斜任意角度。这样PTL+倾斜EDA介质就可以看作周期性的倾斜EDA介质。然后采用加权平均法求得整体的等效弹性系数。

1.1 EDA介质弹性系数的计算

EDA介质如图2所示，计算其弹性系数可以使用Hudson理论。

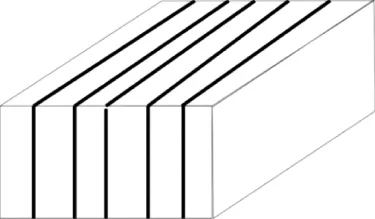
图2 EDA介质

Hudson给出的二阶摄动形式为

(1)

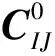
经过推导，含定向排列裂隙介质的弹性系数矩阵为

(2)

其中，C23=C33-2C44，因此描述EDA介质的弹性系数有5个[7]。

1.2 Bond变换

模型每一层的EDA的裂隙面都不垂直于x轴，其方向相当于绕y轴在xoz面旋转了θ角。所以在计算各层的弹性系数加权之前，需要对每一层进行Bond变换，变换矩阵为Mθ[13]。原坐标系下的各层弹性系数矩阵(2)经Bond变换后，其形式为

(3)

1.3 加权平均

根据Backus加权平均法[7]和公式(3)以及附录A中求得的应力与应变的本构关系，可以得到对应的等效弹性系数矩阵:

(4)

其中，

(4)式给出了PTL+倾斜EDA模型的弹性参数计算表达式，而符号“〈〉”表示在垂向(z轴方向)上的加权平均。根据White的理论[14]可以知道，对各薄层弹性参数来说，其对应权函数的值正比于此薄层在整个地质体模型中的厚度的比例。因此，当知道PTL介质各层的纵、横波速度，厚度，密度以及裂隙密度、裂隙纵横比、裂隙填充物后，即可用(4)式求其对应的13个弹性参数。

以上的推导过程中，裂隙的方位角为0，当方位角不为0时，即观测坐标系与本征坐标系之间的夹角为φ，上述弹性系数矩阵还要再旋转一次，旋转矩阵为Mφ，旋转后的弹性系数矩阵为

(5)

这种情况下，共有21个独立的弹性系数，与三斜介质的弹性系数个数相同，此时，准P波、准SH波和准SV波耦合[15]。

2 模拟算例

本文在验证上述含倾斜裂隙页岩介质弹性系数计算方法的正确性时，采用Saenger和Bohlen提出的旋转网格有限差分法，把速度定义在网格单元顶点，应力和弹性系数定义在网格单元中心，这样在计算应力时的所有空间偏导数可以直接求解[16]；采用的吸收边界条件是Cerjan等[17]提出的简单吸收边界。网格点数600×600，网格间距5m，时间步长1ms，爆炸震源，主频30Hz。

如图1所示，方位角(φ)为0，此时观测方向与裂隙走向一致，在这种情况下接收到的y分量始终为0，因此，只给出了裂隙倾角(θ)分别为30°,45°和60°时波场快照中的x分量和z分量。图3到图5分别为裂隙倾角为30°,45°和60°时的波场快照，可以看出,纵波波前面的长轴方向与介质的裂隙方向一致,随着裂隙倾角的旋转而旋转;另外，波场快照中都可以观察到横波分裂现象，产生振幅奇异性，符合吴国忱等[9]和牟永光等[18]文献的论述。由此证明了本文所给出的弹性系数计算方法的正确性和PTL+倾斜EDA模型具有倾角各向异性特征。

图3 含倾斜裂隙(倾角为30°)PTL介质波场快照a x分量; b z分量

图4 含倾斜裂隙(倾角为45°)PTL介质波场快照a x分量; b z分量

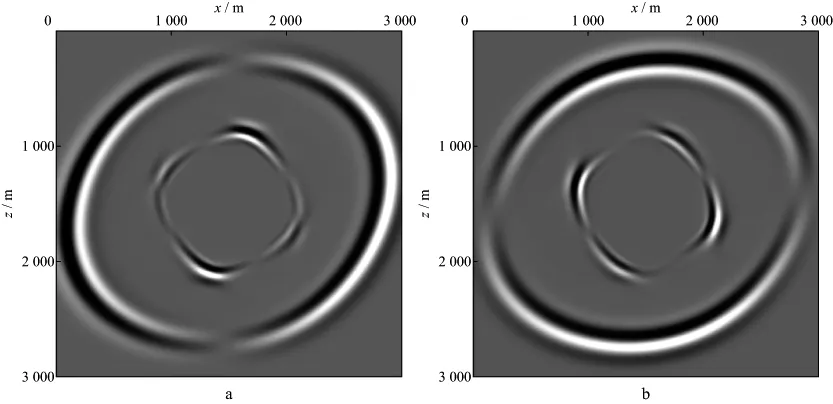
图5 含倾斜裂隙(倾角为60°)PTL介质波场快照a x分量; b z分量

当裂隙方位角为30°和45°，倾角为30°时，正演模拟结果分别如图6和图7所示。图6和图7中P波波前面为椭圆形，横波波前面出现了明显的横波分裂现象。y分量不再为0，出现了SH波;在x分量和z分量上出现SV波，而且SV波和SH波的波形和相位都有所不同。另外，图6和图7的对比结果显示方位角的变化对P波波前面的影响不大，但是会明显影响S波波前面，当方位角为45°时，在垂直于对称轴方向横波不发生分裂，在对称轴方向出现明显快横波。图3到图5中裂隙方位角为0时，纵波波前面呈椭圆状，两段比较尖锐;而图6和图7中，纵波波前面越来越圆。以上这些特点证明了PTL+倾斜EDA介质模型具有方位各向异性特征。

当裂隙含气，裂隙方位角为45°，裂隙倾角为30°时的波场快照如图8所示。对比裂隙饱含水和干燥时的波场快照(图7和图8)可以看出:干燥裂隙，即裂隙含气时，纵波波前面呈明显的椭圆形，横波波前面具有更强的能量，说明裂隙含气时对地震波的传播有显著影响，介质具有更强的各向异性特征。这也说明本文所给出的弹性系数计算方法还可用于研究含裂隙页岩介质中裂隙倾角、裂隙密度和裂隙填充物性质对地震波传播的影响。

图6 含倾斜裂隙(方位角为30°，倾角为30°)PTL介质波场快照a x分量; b y分量; c z分量

图7 含倾斜裂隙(方位角为45°，倾角为30°)PTL介质波场快照a x分量; b y分量; c z分量

图8 含气倾斜裂隙(方位角为45°，倾角为30°)PTL介质波场快照a x分量; b y分量; c z分量

3 结束语

1) 正演模拟结果证明了本文根据Hudson微裂隙理论、Bond变换和Backus加权平均法推导出的含倾斜裂隙页岩介质模型等效弹性系数计算方法的正确性，同时也说明了Backus加权平均法在计算薄互层介质等效弹性系数时的有效性。

2) 正演模拟波场快照中椭圆形波形对称轴随裂隙倾角旋转的情况和随裂隙方位角不同而不同的横波分裂现象，证明了含倾斜裂隙页岩介质模型具有和TTI介质类似的倾角各向异性和方位各向异性特征。

3) 因为本文给出的含倾斜裂隙页岩介质弹性系数由介质各层的纵、横波速度，厚度，密度以及裂隙密度、裂隙纵横比、裂隙填充物等参数直接求出，因此本文方法还可应用于研究薄互层页岩介质中裂隙倾角、裂隙密度和裂隙填充物性质对地震波传播的影响。

附录A

各层的应力和应变的本构关系有

(1)

把σxx，σyy，σxy，uxz，uyz，uzz用σxz，σyz，σzz，uξx，uξy(ξ=x,y,z)表示，由(1)式可得

(2)

其中，

(3)

根据加权平均函数的特殊性质[7]，对(2)式进行加权平均运算，并再次变换本构方程，使应力用应变表示:

(4)

其中，

(5)

根据以上求得的应力与应变的本构关系，即可得到对应的等效弹性系数矩阵。

参 考 文 献

[1] 李新景,胡素云,程克明.北美裂缝性页岩气勘探开发的启示[J].石油勘探与开发,2007,34(4):392-400

Li J X,Hu S Y,Cheng K M.Suggestions from the development of fractured shale gas in North America[J].Petroleum Exploration and Development,2007,34(4):392-400

[2] Hudson J A.Wave speeds and attenuation of elastic waves in material containing cracks[J].Geophysical Journal of the Royal Astronomical Society,1981,64(1):133-150

[3] Hudson J A.A higher order approximation to the wave propagation constants for a cracked solid [J].Geophysical Journal of the Royal Astronomical Society,1986,87(1):265-274

[4] Hudson J A.Crack distributions which account for a given seismic anisotropy[J].Geophysical Journal International,1991,104(3):517-521

[5] Schoenberg M,Douma J.Elastic wave propagation in media with parallel fractures and aligned cracks[J].Geophysical Prospecting,1988,36(6):571-590

[6] Schoenberg M,Helbig K.Orthorhombic media:modeling elastic wave behavior in a vertically fractured earth[J].Geophysics,1997,62(6):1954-1974

[7] 傅旦丹,何樵登.含垂直裂解隙PTL介质长波长等效正交各向异性弹性常数[J].地球物理学报,2002,45(增刊):307-320

Fu D D,He Q D.Elastic constants of long-wavelength effective orthorhombic anisotropy for PTL media containing vertical cracks[J].Chinese Journal of Geophysics(in Chinese),2002,45(S1):307-320

[8] 王德利,何樵登.裂隙型单斜介质中弹性系数的计算及波的传播特性研究[J].吉林大学学报(地球科学版),2002,32(2):91-96

Wang D L,He Q D.Elastic constants calculation method and propagation properties for cracked monoclinic media[J].Journal of Jilin University(Earth Science Edition)，2002,32(2):91-96

[9] 吴国忱,罗彩明,梁楷.TTI介质弹性波频率-空间域有限差分数值模拟[J].吉林大学学报(地球科学版),2007,37(5):1023-1033

Wu G C,Luo C M,Lang K.Frequency-space domain finite difference numerical simulation of elastic wave in TTI media[J].Journal of Jilin University (Earth Science Edition),2007,37(5):1023-1033

[10] 祝贺君,张伟,陈晓非.二维各向异性介质中地震波

场的高阶同位网格有限差分模拟[J].地球物理学报,2009,52(6):1536-1546

Zhu H J,Zhang W,Chen X F.Two-dimensional seismic wave simulation in anisotropic media by non-staggered finite difference method[J].Chinese Journal of Geophysics(in Chinese),2009,52(6):1536-1546

[11] Saenger E H,Bohlen T.Finite-difference modeling of viscoelastic and anisotropic wave propagation using the rotated staggered grid[J].Geophysics,2004,69(2):583-591

[12] Han B,Seol S J,Byun J.Elastic modelling in tilted transversely isotropic media with convolutional perfectly matched layer boundary conditions[J].Exploration Geophysics,2012,43(2):77-86

[13] 孙瑞艳.TTI介质旋转交错网格有限差分及其组合边界条件[D].青岛:中国石油大学(华东),2010

Sun R Y.Rotated staggered grid finite-difference and the combined boundary conditions in TTI media[D].Qingdao:China University of Petroleum(EastChina),2010

[14] White J E.地下的声音-地震波的应用[M]. 陆其鹄，齐国英,译.北京:地震出版社，1986:1-167

White J E.Underground sound:application of seismic wave[M].Lu Q H,Qi G Y,Translator.Beijing: Seismological Press,1986:1-167

[15] 郝奇.三维TTI介质地震波场正演模拟[D].长春:吉林大学,2007

Hao Q.Seismic wavefield modeling in 3D TTI media[D].Changchun:Jilin University,2007

[16] 严红勇,刘洋.黏弹TTI介质中旋转交错网格高阶有限差分数值模拟[J].地球物理学报,2012,55(4):1354-1365

Yan H Y,Liu Y.Rotated staggered grid high-order finite-difference numerical modeling for wave propagation in viscoelastic TTI media[J].Chinese Journal of Geophysics(in Chinese),2012,55(4):1354-1365

[17] Cerjan C,Kosloff D,Kosloff R,et al.A nonreflecting boundary condition for discrete acoustic and elastic wave equations[J].Geophysics,1985,50(4):705-708

[18] 牟永光，裴正林.三维复杂介质地震数值模拟[M].北京:石油工业出版社，2005:75-86

Mu Y G,Pei Z L.Seismic numerical modeling for 3-D complex media[M].Beijing:Petroleum Industry Press,2005:75-86