基于连续小波变换的时频域地震波能量衰减补偿

杨学亭,刘 财,刘 洋,罗 腾,周 寅,张 鹏,李继龙

(吉林大学地球探测科学与技术学院，吉林长春130026)

地震波在地下介质中传播时，由于地层的非弹性性质，使其能量有一定的衰减损耗。国内外专家学者已经对地震波衰减机理和补偿方法进行了大量的研究。应用比较早的有谱白化处理和反Q滤波。谱白化是通过展平信号的振幅谱来实现对衰减频率的补偿，可分别在时间域和频率域进行。谱白化处理的特点是只对信号的振幅谱进行处理而不改变信号的相位谱。反Q滤波最早由Hale提出[1]。Hargreave等[2]提出与Stolt偏移原理类似的相移校正方法，采用级联式常Q补偿的方式开时窗逐级向下计算。Wang提出一种基于波场延拓理论的反Q滤波方法[3]，并于2006年对该方法作了改进，推广到Q随着地层深度连续变化的情况[4]。

大地滤波算子是时间、频率和品质因子的函数，因此也可以在时频域内进行地震波能量衰减补偿。白桦等[5]提出了时频域的衰减补偿方法，将短时傅里叶变换(STFT)应用到衰减补偿中。针对STFT时窗宽度固定，不能根据非平稳地震信号在不同时刻的不同特征调节时窗宽度的问题，李鲲鹏等[6]提出基于小波包分解的地震波能量衰减补偿方法。刘喜武等[7]提出了基于广义S变换的地震波能量衰减补偿方法。Braga等[8]提出基于一维连续小波变换的小波域内地震波能量衰减补偿方法，取得了很好的效果，文中将尺度和频率的关系定义为s=f0/f(f0是小波的中心频率)。小波变换是一种时间-尺度分析方法，每一个尺度对应着一个频带而非单一的频率，尺度和频率之间没有严格的数学关系。

本文利用Sinha等[9]提出的基于一维连续小波变换的时频谱(TFCWT)和基于Kolsky衰减模型的大地滤波算子，在时频域内实现地震波能量的衰减补偿。对比文献[8]提出的小波域(时间-尺度域)内的衰减补偿方法，基于TFCWT的地震波能量衰减补偿方法能够更好地恢复地震波的振幅和相位，提高地震资料的分辨率。

1 理论基础

1.1 基于一维连续小波变换的时频谱

短时傅里叶变换(STFT)和Gabor变换都是时频分析常用的方法，但是这些方法的时频窗口是固定的，窗口的大小直接决定了时频分辨率。一旦窗口函数选定，其时频分辨率就已经确定，不会随着时间和频率而改变，因此不能满足对时频分辨率的要求。

相反，小波变换不需要预先设定窗口的宽度，它利用平移参数τ和尺度参数s得到时间-尺度谱。小波变换具有很好的时间和频率局部分析的能力。一维连续小波变换公式如下:

设信号f(t)∈L2(R)，ψ(t)为小波基函数

(1)

式中:s为尺度参数;τ为平移参数。且小波基函数需要满足可容性条件

(2)

式中:Ψ(ω)是ψ(t)的傅里叶变换;Cψ对每一个小波基函数是一个常数。则满足相容性条件的一维连续小波变换为

(3)

小波函数的选取是应用小波变换的一个重要问题，在此选用的是Morlet小波

(4)

Morlet小波是一种复小波基函数，利用Morlet小波函数可以将信号的振幅和相位分开，有利于非平稳信号的分析处理[11]。Morlet小波作为一种分析小波，已经被认为是分析非弹性介质中非平稳地震信号最合适的小波。Kulesh等[12]将Morlet小波应用于天然地震学中确定表面波的传播参数，群速度、相速度和衰减系数等。Reine等[13]将Morlet小波应用于反射波地震学。

根据Addison[11]，一维连续小波变换在频率域内的计算公式为

(5)

对尺度参数s的选择，采用Christopher等[14]提出的方式，经过频率域内的小波变换得到时间-尺度谱。

Hlawatsch等[15]提出利用关系式s=f0/f(f0是小波中心频率)可以将时间-尺度谱转化为时频谱。Sinha等[9]利用该数学关系式实现了时间-尺度谱到时频谱的转换，其结果显示在高频部分，时频分析并未取得很好效果，因此提出一种新的方法，对一维连续小波变换的反变换做傅里叶变换，即可得到时频谱，具体公式推导如下:

首先，根据Daubechies[16]给出的反小波变换的公式

(6)

对式(6)进行傅里叶变换得到:

(7)

一维连续小波变换中，在任何尺度s和时间t上，窗口面积ΔtΔω保持不变，即时频分辨率相互制约，但是尺度参数s和平移参数τ是相互独立的[9]，因此可以去掉对平移参数τ的积分，然后把F(ω)替换为F(ω,τ)，得到:

(8)

由方程(8)，就可以利用一维连续小波变换得到时频谱，称之为TFCWT。对信号的重构可以分两步进行:首先对F(ω,τ)按照时间方向进行叠加求和，然后对叠加和做反傅里叶变换。

这里通过对模拟信号的处理，实现基于TFCWT的时频分析，并与Gabor变换方法对比分析。选取chirp信号，信号的频率以对数的方式增加，频率范围是20～120Hz，得到如图1所示的时频谱。

图1 chirp信号的时频谱a chirp信号; b 基于Gabor变换的时频谱; c基于TFCWT的时频谱

从图1中可以看出，在高频部分，基于TFCWT方法更有优势。由于一维连续小波变换可以利用尺度参数和平移参数的相互调节，使其具有更好的局部时频分析能力。

通过对非平稳信号做基于TFCWT的时频谱，然后做反变换重构原信号，最后做误差分析(图2)，以验证方法的正确性。

分析图2可以看出,TFCWT时频分析方法对非平稳信号具有很好的分析能力。通过求取原信号和重构信号的误差，验证了TFCWT时频分析方法以及信号重构方法的正确性。

1.2 线性衰减模型和衰减地震道的构建

在勘探地震学中，常用由Kolsky[17]提出的衰减模型，假设衰减因子λ是频率f的线性函数(Q≥1)。根据Kolsky的模型，衰减因子和相速度分别为

(9)

式中：vr和fr分别表示参考相速度和参考频率。

Wang[18]提出了一种衰减模型，其基本理论是在均匀粘弹性介质中，波数k变成了一个关于相速度v，衰减系数λ和频率f的复数k(f)=2πf/v+iλ。经过测试发现，把fr设置为大值(比如500Hz)更有利于对扩散的恢复。将(9)代入到复波数k(f)

(10)

通过在频率域内求解Helmoltz方程的平面波解，可以推导出频率域内衰减信号S(f)和原信号S0(f)之间的关系为

(11)

式中:ζ表示波前面沿着射线路径从震源到检波器的距离。将(10)代入(11)中，因为在勘探地震学中常用的Q值范围是20～200，因此可以忽略含有1/Q2的项，化简得到

(12)

图2 非平稳信号的时频谱及其信号重构a 非平稳信号; b 基于TFCWT的时频谱; c 重构信号; d 误差分析

(12)式中并对所有的频率进行叠加，得到时间域内的衰减地震道为

(13)

这就得到了基于Kolsky衰减模型的衰减地震道。滤波算子G是时间和频率的函数，由此可以实现在时频域内对衰减信号进行补偿。

1.3 时频域内地层衰减补偿

定义反Q滤波算子为

(14)

(15)

2 理论模型测试分析

2.1 合成地震信号的衰减补偿

采用主频f0=50Hz的Ricker子波合成地震信号(图3a)，时间采样间隔为dt=0.004s，最大延续时间tmax=1.2s;品质因子Q=80，采用Kolsky衰减模型合成衰减地震信号(图3b)。分别在基于一维连续小波变换的小波域和TFCWT时频域内做地震波能量衰减补偿(图4)。图4a，图4c和图4e 是合成地震信号在小波域(时间-尺度域)内的衰减补偿，可见，补偿信号在振幅和相位上都得到较好恢复;图4b，图4d和图4f是合成地震信号在TFCWT时频域内进行的能量衰减补偿，可见，振幅和相位的补偿效果都比在小波域内好。原因可能是小波域内衰减补偿定义尺度和频率的关系为s=f0/f，这并不是它们之间严格的数学关系。

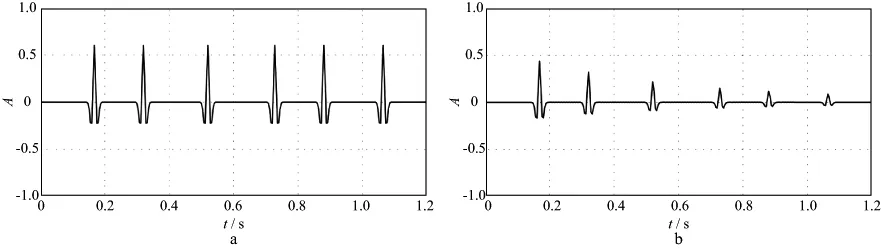
图3 合成地震信号(a)及其基于Kolsky模型的衰减地震信号(b)

图4 合成地震信号在小波域和TFCWT时频域内的衰减补偿a 衰减信号的时间-尺度谱; b 衰减信号基于TFCWT的时频谱; c 衰减补偿后信号的时间-尺度谱; d 衰减补偿后信号的时频谱; e 小波域内衰减补偿后的信号; f 时频域内衰减补偿后的信号

2.2 模拟地震记录的衰减补偿

采用主频f0=50Hz的最小相位子波，白噪的反射系数序列，通过正演获得模拟地震记录，时间采样间隔为dt=0.004s，最大延续时间tmax=1.2s;品质因子Q=80，基于Kolsky模型合成衰减记录，在TFCWT时频域内做衰减补偿(图5)。

对比图5a至图5c可以看出，基于一维连续小波变换的时频分析方法能够分析非平稳的地震信号，在TFCWT时频域内做地层衰减补偿能够很好地补偿深层信号的振幅和相位，大的反射层位都得到了很好的恢复，分辨率明显提高。

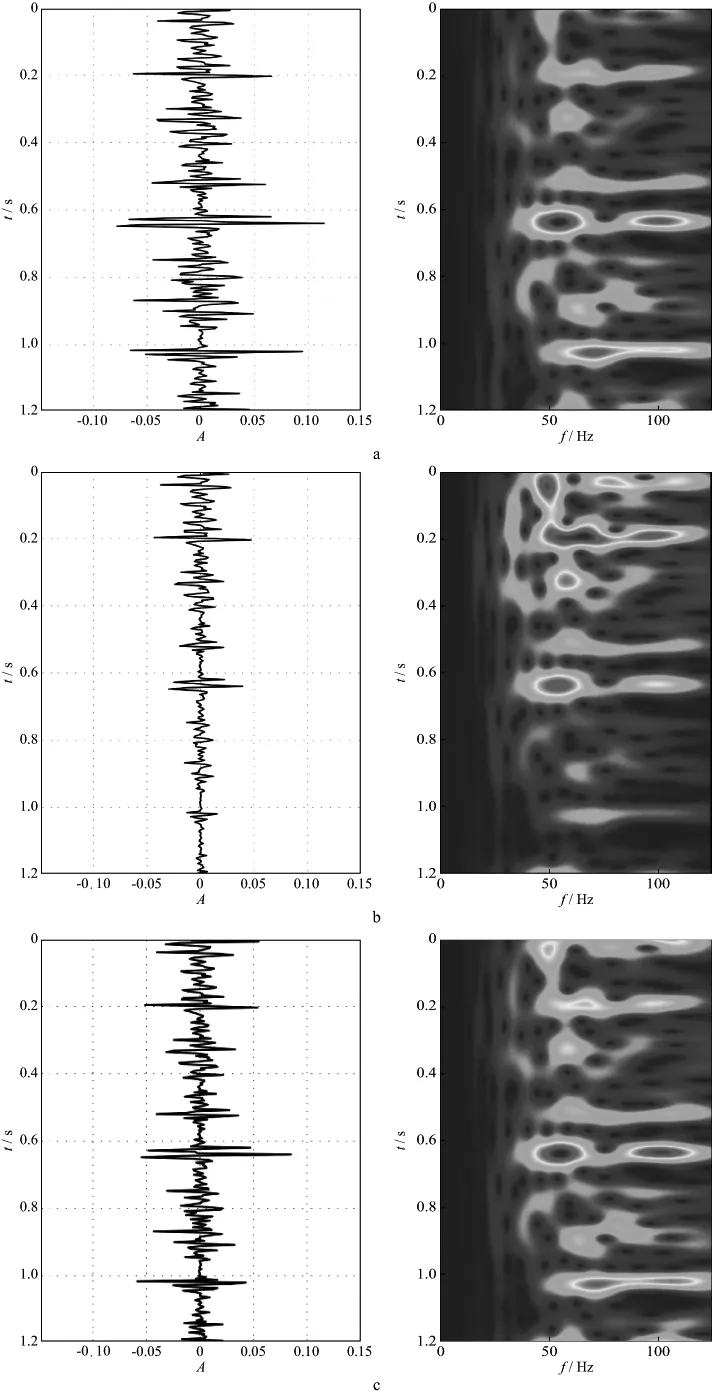
图5 模拟地震记录在TFCWT时频域内的衰减补偿a 模拟地震记录及其时频谱; b 衰减地震记录及其时频谱; c衰减补偿后的时频谱及重构信号

3 实际地震资料试处理

利用某地区的实际二维叠后地震资料进行本文方法的试处理。图6a是选取的其中第212～301道(1.6～2.2s)实际地震数据，该数据的时间采样间隔为1ms;图6b是利用基于TFCWT的地震波能量补偿方法进行补偿处理后的结果。

对比图6a和图6b可以看出，地震波能量得到了很好的补偿，补偿后的剖面上反射波同相轴更加清晰，深层分辨率得到了明显的改善。实际资料试处理结果说明基于TFCWT的地震波能量补偿方法对大地滤波衰减具有很好的补偿和恢复作用，能够较好地提高地震资料的分辨率。

图6 某地区二维叠后地震资料(a)及其基于TFCWT时频域内地震波能量补偿后的结果(b)

4 结束语

一维连续小波变换具有很好的局部分析能力，利用一维连续小波变换可以得到时间-尺度谱，每个尺度表示的是一个频带而不是单个频率。通过对一维连续小波变换的反变换做傅里叶变换得到时频谱，就是基于一维连续小波变换的时频分析方法。Kolsky模型的大地滤波算子是时间和频率的函数，因此可以实现在时频域内做地震波能量的衰减补偿。理论模型和实际地震资料试算的结果表明，基于TFCWT的地震波能量补偿方法能够很好地补偿深层衰减地震信号，提高地震资料分辨率，其应用效果优于小波域衰减补偿方法。

参 考 文 献

[1] Hale D.An inverse Q filter[J].SEP,1981,26(22):231-243

[2] Hargreaves N D,Calvert A J.Inverse Q filtering by Fourier transform[J].Geophysics,1991,56(4):519-527

[3] Wang Y H.A stable and efficient approach of inverse Q filtering[J].Geophysics,2002,67(2):657-664

[4] Wang Y H.Inverse Q-filter for seismic resolution enhancement[J].Geophysics,2006,71(3):51-61

[5] 白桦,李鲲鹏.基于时频分析的地层吸收补偿[J].石油地球物理勘探,1999,34(6):642-648

Bai H,Li K P.Stratigraphic absorption compensation based on the time-frequency analysis[J].Oil Geophysical prospecting,1999,34(6):642-648

[6] 李鲲鹏,李衍达,张学工.基于小波包分解的地层吸收补偿[J].地球物理学报,2000,43(4):542-549

Li K P,Li Y D,Zhang X G.A method to compensate earth filtering based on wavelet packet[J].Chinese Journal of Geophysics,2000,43(4):542-549

[7] 刘喜武,年静波,刘洪.基于广义S变换的吸收衰减补偿方法[J].石油物探,2006,45(1):9-14

Liu X W,Nian J B,Liu H.The absorption attenuation compensation method based on the generalized S transform[J].Geophysical Prospecting for Petroleum,2006,45(1):9-14

[8] Braga I L S,Moraes F S.High-resolution gathers by inverse Q filtering in the wavelet domain[J].Geophysics,2013,78(2):53-61

[9] Sinha S,Routh P S,Anno P D,et al.Spectral decomposition of seismic data with continuous-wavelet transform[J].Geophysics,2005,70(6):19-25

[10] 许惠平,周云轩，孙运生，等.小波和球面小波技术及其在位场分析中的应用[M].北京:科学出版社，2004:3-40

Xu H P，Zhou Y X,Sun Y S,et al.Wavelet and spherical wavelet theories and their applications in potential field[M].Beijing:Science Press,2004:3-40

[11] Addison P S.The illustrated wavelet transform handbook:Introductory theory and applications in science,engineering,medicine and finance[M].London:Institute of Physics Publishing,2002:6-63

[12] Kulesh M,Holschneider M,Diallo M S,et al.Modeling of wave dispersion using continuous wavelet transforms[J].Pure and Applied Geophysics,2005,162(5):843-855

[13] Reine C,Baan M van der,Clark R.The robustness of seismic attenuation measurements using fixed and variable window time-frequency transforms[J].Geophysics,2009,74(2):123-135

[14] Torrence C,Compo G P.A practical guide to wavelet analysis[J].Bulletin of the American Meteorological Society,1998,79(1):61-78

[15] Hlawatsch F,Boudreaux-Bartels G F.Linear and quadratic time-frequency signal representations[J].IEEE Signal Processing,1992,9(2):21-67

[16] Daubechies I.Ten lectures on wavelets[M].SIAM:Society of Industrial and Applied Mathematics,1992:1-355

[17] Kolsky H.The propagation of stress pulses in viscoelastic solids[J].Philosophical Magazine,1956,1(8):693-710

[18] Wang Y H.Seismic inverse Q filtering[M].New York:Wiley-Black well,2008:1-248