Mathematical modeling for selecting center locations for medical and health supplies reserve in Hainan Province

Xiao-Hua Hu, Chuan-Zhu Lu, Min Li, Cai-Hong Zhang, Hua Zhang*

1No. 99 Longkun South Road, Hainan Normal University, Haikou, China

2Hainan Medical University, Haikou, China

3Hainan Provincial People's Hospital, Haikou, China

Mathematical modeling for selecting center locations for medical and health supplies reserve in Hainan Province

Xiao-Hua Hu1, Chuan-Zhu Lu2, Min Li3, Cai-Hong Zhang2, Hua Zhang2*

1No. 99 Longkun South Road, Hainan Normal University, Haikou, China

2Hainan Medical University, Haikou, China

3Hainan Provincial People's Hospital, Haikou, China

Objective: To explore how to choose the center locations to build the medical and health supplies reserve among many island towns. Methods: The center locations were selected from 18 towns Hainan Province, it’s maximum service range (distance) was required to reach the minimum, or to minimize. Results: Three scenarios were considered, the center locations included only one town, two towns, three towns. By the use of graph theory and MATLAB programming, a mathematical model was established to obtain the shortest distance and the shortest path between arbitrary two towns. Conclusions: We find out the center sites under certain conditions, and determine the specific service ranges of the center sites.

ARTICLE INFO

Article history:

Received 10 September 2013

Received in revised form 15 October 2013

Accepted 15 December 2013

Available online 20 Februany 2014

Graph theory

1. Introduction

With special geographical position and geological structure, Hainan province is regarded as an island area that the various natural disasters could occur frequently, such as typhoon, tsunami, earthquake, flood, fireetc. Hainan is located at the national border area and fortified with military base, currently facing Southeast Asia national complicated political, military and natural disaster environment. With the rapid development of Hainan Provincial economy, diversified culture in recent years, and the large chemical enterprises entering to Hainan island’s western zone, we are also under the risk of non-natural disaster events, such as mass chemical poisoning, explosion, prevalence of the infectious disease, the sea and air transportation accidents, and the threat of terrorist attacks. Due to the establishment of Yangpu Economic Development Zone and Space city, it is imperative to build a relatively independent of disaster medical rescue system[1-7] in Hannan island. In addition, Hannan province is blessed with the geographical features of island, it is connected with surrounding regions by two kinds of transportations, either by air, or by sea, but once the earthquake, typhoon, tsunami occur, none of traffic ways are often passable and readily reachable, so self-help and island’s internal rescue capacity is even more important and effective than external assistance from other provinces and areas in China. On December 31, 2009, the State Council of China issued a white paper of “Recommendations on promoting the construction development of Hainan international tourism island”[8]. In it, the constructing Hainan as an international tourism became one of the national strategies. Thus, the construction of Hainan to be an international tourism island officially is well on track. As the China major strategic plan, Hainan Island will be built to be the world’s top-class leisure resort in 2020, it will be made to be an open island, and a green island, a civilization and harmonious island, so, it is strategically important and significant to set up a medical and health supplies reserve, in quickly responding to the natural and non-natural risk or disasters.

2. Mathematical modeling and results

There were eighteen major towns in Hainan province. These towns were Lingao (1), Danzhou (2), Changjiang(3), Dongfang (4),Ledong (5), Sanya (6), Baoting (7), Lingshui (8), Wanning (9), Qionghai (10), Ding’an (11), Wenchang (12), Haikou (13), Chengmai (14), Tunchang (15),Baisha(16), Wuzhishan (17), Qiongzhong (18). For convenience of modeling, city’s names were denoted by a number with in the parentheses 1,2,3,..., 18, respectively, First of all, an adjacent matrix was established[9] between two towns, the resultant matrix was as below

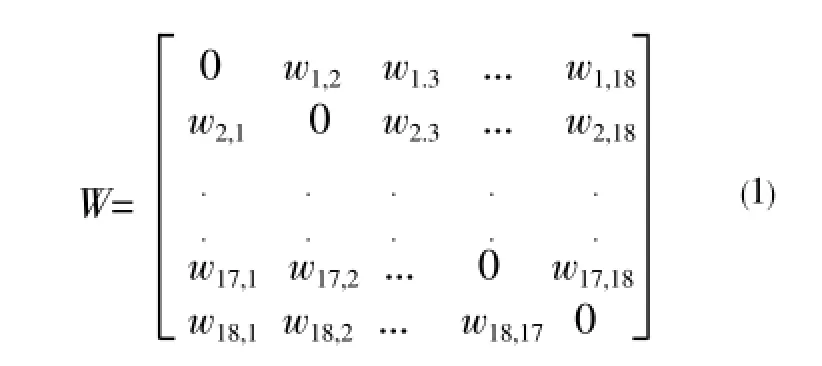
Wherewi,j=wj,i,i,j=1,2,...,18, denotes the distance (km) between the town and the town . All the distance data of 18 Hainan towns[10] was shown in Table 1.

2.1. One center point (town) case

A center point (town) was selected from eighteen major towns in Hainan Province to build the medical and health supplies reserve. The maximum service range (distance) of the medical and health supplies was required to be the shortest distance to reach all towns of Hainan island[11-13]. First it was assumed that all towns have the required infrastructure and are eligible to be built such a reserve, and the roads connected arbitrary two towns are passable, and the length of path are known. By use of Floyd algorithm[14], the shortest distance matrixD=(dij),i,j=1,1,...,18, and the shortest path index matrixRcould be found between any two points(towns), wheredijdenoted the shortest distance between arbitrary two towns. If the center point was taken to be the town , then the maximum service distance(range) ofviwas as below:

To search for an integer , such that:

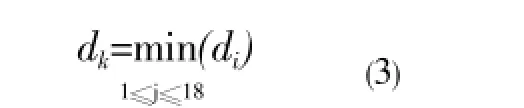
then the pointvkwas the town to find. The maximum service distance (range) ofvkcould reach the minimum. The specific process was as follow, by MATLAB programming[15], to obtain the maximum values of each line in the matrixD=(dij),i,j=1,2,...,18, the minimum value was taken out from these maximum values. The point corresponding to the minimum value was the target town. Calculating results showed that the minimum value was 219.9 km, andvk=18, or Qiongzhong was the center town (point). Further more, the shortest distance and the corresponding path to the rest of 17 towns from Qiongzhong could be determined and given as follows. The shortest distances from Qiongzhong(18) to Lingao (1), to Danzhou (2), to Ledong (5), to Sanya (6), to Baoting (7), to Lingshui (8), to Wanning (9), to Qionghai (10), Ding’an (11), to Haikou (13), to Chengmai (14), to Tunchang (15), to Baisha(16), to Wuzhishan (17) were 143.6 km, 86.2 km,101.3 km, 141.0 km, 108 km, 91.2 km, 82.3 km, 125.2 km, 125.9 km, 142.0 km, 105.2 km, 52.7 km, 70.9 km, 77.1 km, respectively. The corresponding path are direct (no middle point), but the shortest distance was 161.7 km from Qiongzhong (18) to Changjiang (3), the corresponding path was from Qiongzhong (18) to Danzhou (2) to Changjiang (3). The shortest distance was 219.9 km from Qiongzhong (18) to Dongfang (4), the corresponding path was Qiongzhong (18) to Danzhou (2) to Changjiang (3) to Dongfang (4). The shortest distance was 184 kilometers from Qiongzhong (18) to Wenchang (12). The corresponding path was Qiongzhong (18) to Qionghai (10) to Wenchang (12) (Figure 1).

Figure 1. One center point (town) case.

2.2. Two center points (towns) case

Two center points (towns) were selected as the medical and health supplies reserve from eighteen main towns in Hainan Province. The maximum service range (distance) of two center points was required to reach the minimum, or to minimize. The basic assumptions about the towns were the same as the previous case. It was assumed that two center points are located at the pointsshortest distance from the pointvkto two center pointsvi,vj.

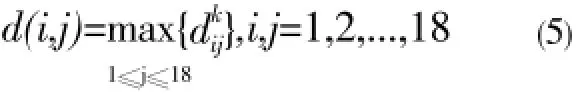
To search for two integers, such as that:

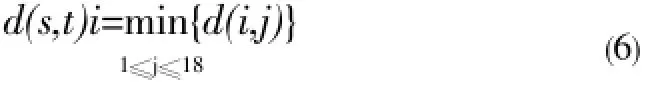
Then the pointvs, vtwere the places or twons. The maximum service distance (range) ofvs, vtreached the minimum. By MATLAB programming, in order to obtain the matrixD324×the maximum values of each line was taken in the matrixD324×18. Then, the minimum value from these maximum values was taken out. The pointsvs, vtwhich correspondwd to the minimum value, were the target townsand townt. Calculating results showed that the minimum value was 143.9 km:

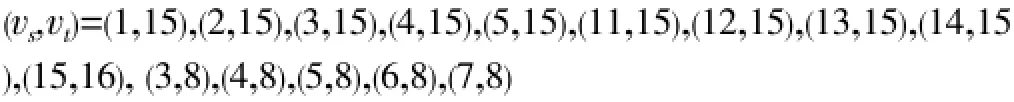
However, in the actual situation, the shortest distance between the pointvsandvtwas more than 143.9 km (otherwise, there was no point to choose two center points), and the pointvsand pointvtwith the respective maximum service distance was at most 143.9km, the final result of calculation was (vs,vt)=(5,15) that was , Ledong (5) and Tunchang (15), the shortest distance between Ledong (5) and Tunchang (15)was 152.3 km . The service ranges of Tunchang (15) covered Lingao(1), Danzhou (2),Lingshui (8), Wanning (9), Qionghai (10), Ding’an (11), Wenchang (12), Haikou (13), Chengmai (14) and Tunchang (15); while the service ranges of Ledong (5) included Changjiang (3), Dongfang (4), Ledong (5), Sanya (6), Baoting (7), Baisha(16), Wuzhishan (17) and Qiongzhong (18).

2.3. Three center points (towns) case

Now, three center points (towns) were selected to build the medical and health supplies reserve from eighteen major towns in Hainan Province. Similarly, the maximum service range (distance) of three center points was required to reach the minimum, or to minimize. It was assumed that three center points are located at the pointsto denote the shortest distance from the point to three center pointsvi, vj, vk.

To identify three integers, t, p, such that

then the pointvs,vt,vpwere the target places. The maximum service distance (range) ofvs,vt,vpreached the minimum. In the same approach of MATLAB programming, in order to obtain the matrix,maximum values of each line in the matrixD5832×18, and the minimum value was taken out from these maximum values. The pointsvs,vt,vpcorresponding to the minimum value were the towns, towntand townp. Calculating results showed that the minimum value was 105.2 km. However, a total of 446 groups met the requirement, there was three points in each group. However, Considering the actual situation, the shortest distances between the arbitrary pair of pointsvs,vtandvpwere more than 105.2 km (otherwise, there was no meaning to choose three center points), and the pointvs,vtand pointvpwith the respective maximum service distance was at most 105.2 km.The final result of calculation was (vs,vt,vp)=(3,11,17) that is to say , Changjiang (3), Ding’an (11)and Wuzhishan (17). Further more, the shortest distance between Changjiang (3) and Ding’an (11) was 212 km, the shortest distance between Ding’an (11) and Wuzhishan (17) was 201.6 km, the shortest distance between Ding’an (3) and Wuzhishan (17) was 179.7 km. As a result, the service ranges of Changjiang (3) included Lingao(1), Danzhou (2), Changjiang (3) and Dongfang (4), while the service ranges of Ding’an (11) were Wanning (9), Qionghai (10), Ding’an (11), Wenchang (12), Haikou (13), Chengmai (14) and Tunchang (15). Finally the service ranges of Wuzhishan (17) covered Ledong (5), Sanya (6), Baoting (7), Lingshui (8), Baisha(16), Wuzhishan (17) and Qiongzhong (18).

Table 1 Distance (km) between arbitrary two towns in Hainan provincial eighteen towns.

Table 2 Site selection results in eighteen towns of Hainan Province.

3. Analysis and model improvement

We represent the results from the previous section in Table 2 as below.

The above center points (despite case one, case two or case three) we have selected only consider “the equally important” for eighteen towns of Hainan province, or only consider the geographical position of these towns. We have not taken into consideration of the town’s population, the size of area, and other factors. If each vertex (such as towns) of the graph are endowed with a respective weight (such as population number), and the weight condition of each vertex are taken into account, we may further consider of “weighted center” location problem[16].

In this article, we represented eighteen major towns in Hainan Province as eighteen points, by using the relevant knowledge in Graph theory, with the mathematical software MATLAB, the shortest distance and the shortest path between arbitrary two towns are determined. We respectively established mathematical models on condition of medical and health supplies reserve under one center point, two center points and three center points, through the program calculation the specific center locations of medical and health supplies reserve can be finally determined and the service range of the center points in three cases are also given respectively (Table 2).

Conflict of interest statement

We declare that we have no conflict of interest.

[1] Lu CZ. Imagine construction the disaster medical rescue system of Hainan province. Chin J Hospital Administration 2008; 24(11): 728-731.

[2] Zhang LY. Enhancing summarization of experience of medical rescue after Wenchuan earthquake. J Traumatic Surg 2008; 5: 385-387.

[3] Qin SQ, Wang D, Zhang LL. Geographic information system and the position of GIS for disaster medical rescue. Chin J Social Med 2009; 5: 257-259.

[4] Yan QY, Zhang L, Cai XH. Thinking about knowledge management of remedy of TCM based on the wenchuan earthquake. Chin J Social Med 2009; 5: 268-270.

[5] Hu WJ, Song LT. Actuality and suggestions of domestic medical relief system for flood disaster. Military Med J South China 2011; 1: 60-62, 77.

[6] Cao L. Disaster relief medical practice innovation ideas active health and disease prevention strategies. Chin J Nosocomiol 2011; 18: 3906-3907.

[7] Cheng TM, Su YP, Hu YM, Xiao Y. Exploration on the engineering management of medical rescue in severe natural disaster. Engineering Sci 2009; 6: 63-67.

[8] [Online] Available from: http://news.qq.com/a/20100104/001275.htm.

[9] Xue Y. Mathematical modeling foundation. Beijing: Beijing University of Technology Press; 2004.

[10][Online] Available from:http://tourism.hainan.gov.cn/goverment/ index.html.

[11] Yang J, Wang L, Zheng N, Yang C. Study on the distribution center location problem of perishable product with multi-usage. Chin J Manag Sci 2011; 1: 91-99.

[12] Hu XM, Zhang Y, Li ZP. The vehicle route scheduling location problem of multiple distribution centers and its solution: An SPSS and genetic algorithm based approach. Logistics Technol 2010; 1: 83-86.

[13] Jiang LJ, Jiang M, Zhao ZJ. An overview of literatures on research into location problem of distribution center. Logistics Sci-Tech 2008; 4: 31-33.

[14] Zhao J. Mathematical modeling and mathematical experiments. 3rd edition. Beijing: Higher Education Press; 2007.

[15] Xue DY. Scientific computing language MATLAB5.3 program design and application. Beijing: Tsinghua University Press; 2000.

[16] Wang HY, Huang Q. Graph theory algorithm and the realization of MATLAB. Beijing: Beihang University Press; 2010.

*Corresponding author: Hua Zhang, Hainan Medical University, Haikou, China.

Email: zhanghuashelley@hotmail.com

Foundation project: It is supported by National Natural Science Foundation (81060160); National Natural Science Foundation (71263014); Natural Science Foundation of Hainan Province (811209); Natural Science Foundation of Hainan Province (110005).

Shortest distance and shortest path

Medical and health

Site selection