涡流检测的厚涂层高精度方法

岳秀芳，王召巴，张东利

(中北大学，电子测试技术国家重点实验室，山西太原　030051)

0　引言

随着无损检测技术的发展，涡流检测以其非接触测量、不需要耦合剂、不受油污介质影响、灵敏度高、结构简单、检测速度快和易于实现自动化等优点，越来越广泛地应用在石油、天然气管道可靠性检测，铁道车辆、车轨质量监测，以及发动机包覆层和金属基体材料表面油漆等涂覆层厚度测量中[1]。目前国内生产的涂镀层涡流测厚仪测量范围一般在几百μm，大量程时测量精度为±3%H(H为提离距离)，很难满足一些厚涂镀层高精度的涡流测厚要求。

针对涡流测厚，近些年国内外的研究虽取得了一定成果[2-7]，但主要集中在提高薄涂层和薄金属板的厚度测量以及仿真研究中。例如，文献[2]利用涡流法检测特种碳纤维复合材料绝缘涂层的有效测量范围约为30～800 μm，测量精度约为±20～30 μm．文献[3]针对铁磁性基体材料上非铁磁性薄涂镀层厚度测量，研制了一种测量范围在0～30 μm，测量精度为0.5 μm±3%测量值的智能、高精度涡流测厚仪。文献[5]通过采用高频涡流法对10～200 μm超薄金属薄片进行了厚度测量研究。

文中对比检测仪中涡流信号与提离距离的标定方法，采用4次多项式、幂函数、复合指数和高斯函数对涡流信号与提离距离进行标定，分析标定后的测量误差，研究提高涡流厚涂层测量精度的方法。

1　涡流测厚原理

利用涡流提离效应进行涂镀层厚度测量的原理如图1所示。涡流探头检测线圈紧贴涂镀层表面，涡流探头相对于金属基体的提离距离x即为涂镀层厚度d。由于涡流检测是建立在电磁感应基础上的，检测信号的强度和分布受试件基体材料的电导率σ、磁导率μ、厚度h和检测线圈的激励电流i、激励频率f、提离距离x等因素的影响[8-9]。当提离距离x发生改变时，在有效磁场范围内，进入金属试件的磁通量将发生改变，进而影响线圈与金属试件间的耦合程度。这种相互影响，通过归一化处理，变成阻抗平面内涡流信号幅值的变化[10]。通过对涡流信号幅值与标准提离距离进行标定，得到提离距离与涡流信号幅值对应的关系曲线。检测时，依据涡流信号幅值的变化，即可得到涂层厚度d。

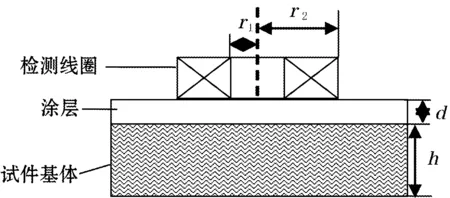
图1　涂层涡流测厚原理

2　涡流测厚平台

涡流检测仪采用ECC-2004智能多功能电磁检测仪；涡流探头依工程需要和实际试件及检测厚度选用可以直接测量线圈阻抗变化的绝对式涡流探头(参数如图2所示)。基体试件选取198 mm×100 mm×5 mm的不锈钢平板。为保证准确的提离距离，使用标准试块(ISO9001)对涡流探头进行提离。如图3所示，U槽导轨固定在支架上，通过U槽导轨内的滚动钢珠使移动支架可以上下移动，探头通过探头夹具固定在移动支架上，随着移动支架移动；通过在固定螺母和U槽导轨之间添加不同的标准试块实现对涡流探头的准确提离。由于提离产生的涡流信号经过常规涡流探头转换器输入EEC-2004涡流检测仪，进行前置放大、相敏检波、平衡滤波、相位旋转和增益放大后，再经过A/D转换输出在阻抗平面内。

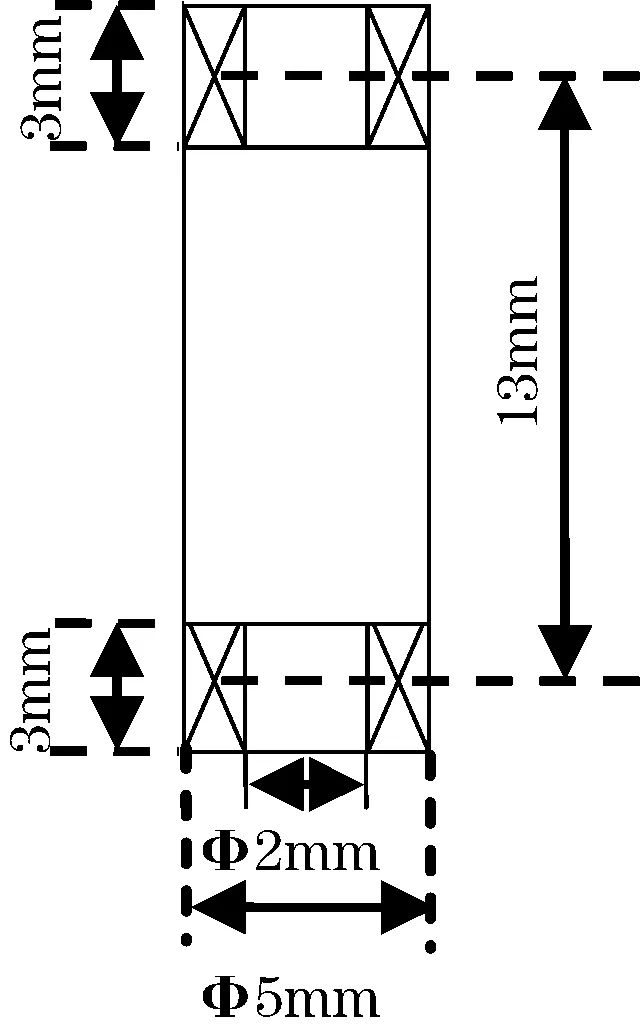
图2　涡流探头参数

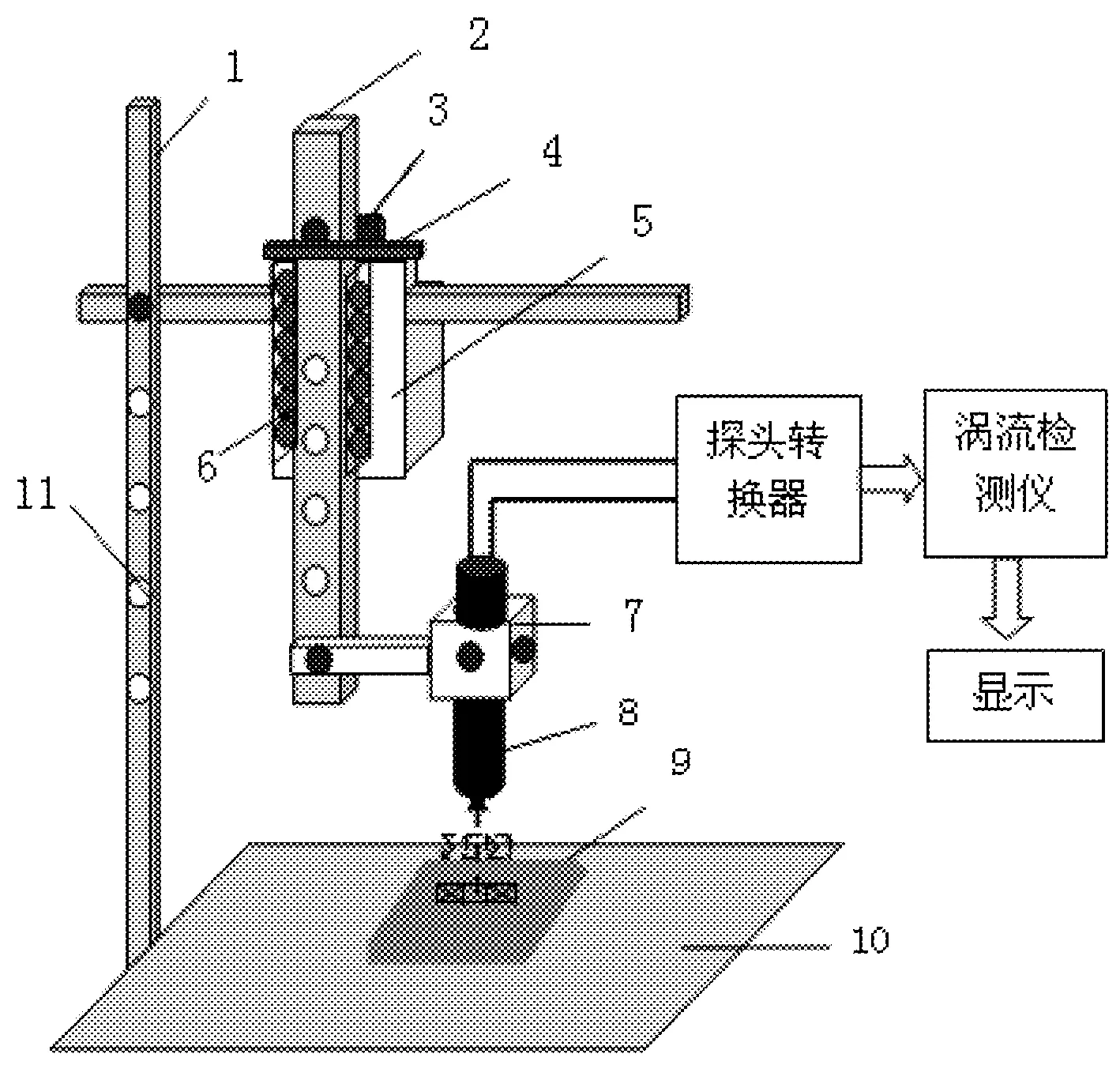
1—固定支架；2—移动支架；3—固定螺母；4—标准试块；5—U槽导轨；6—滚动钢珠；7—探头夹具　8—探头；9—基体试件；10—试验平台；11—调距螺孔

3　试验数据的分析处理

3．1提离距离与涡流信号幅值的关系

依涡流的渗透深度和趋肤效应，将涡流探头激励频率、前置和驱动分别设置为18 181 Hz、25 dB和5。为方便观察，阻抗平面频率、增益和相角分别设置为18 181 Hz、17 dB和226。选取0 mm提离时的涡流信号阻抗幅值为零参考点，通过改变不同的标准试块，获得不同提离距离下的涡流信号阻抗幅值(如图4)。

由图4可看出，涡流信号阻抗幅值与提离距离呈非线性趋势变化。在0～5 mm时，提离距离的微小变化即可引起阻抗平面内涡流信号幅值的明显变化；随着提离距离的增大，阻抗平面内涡流信号的幅值变化越来越小，当提离距离达到10 mm(即涡流探头外径的2倍)时，涡流信号变化趋于零，在实际检测中很难再通过涡流信号准确推断提离距离。

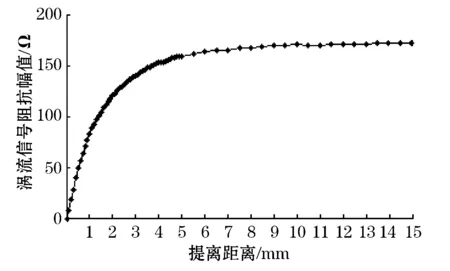
图4　涡流信号与提离距离关系图

3．2提离距离的标定

检测中，为通过涡流信号判断涡流检测的厚度，必须先对标准厚度的涡流信号进行标定，然后把检测材料的涡流信号与之对比，得出检测厚度。ECC-2004检测仪中有二次曲线、指数曲线和插值3种涡流信号与提离距离的标定方法。由于实际检测中，测量误差较大，不能满足测量要求。为提高检测精度，结合涡流检测信号与提离距离的非线性关系和涡流传感器的应用特性，在0～5 mm提离范围内，每隔0.1 mm改变1次提离距离，获得不同提离距离下的涡流信号，分别选用4次多项式、幂函数、复合指数和高斯函数对涡流信号与提离距离进行标定，分析拟合数据和提离误差。4种函数拟合的关系图分别如图5～8所示。

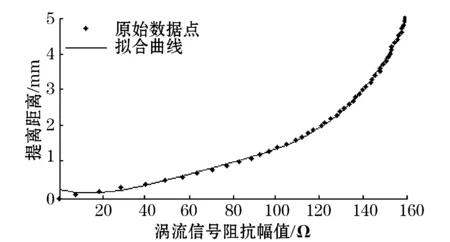
图5　4次多项式拟合涡流信号与提离距离

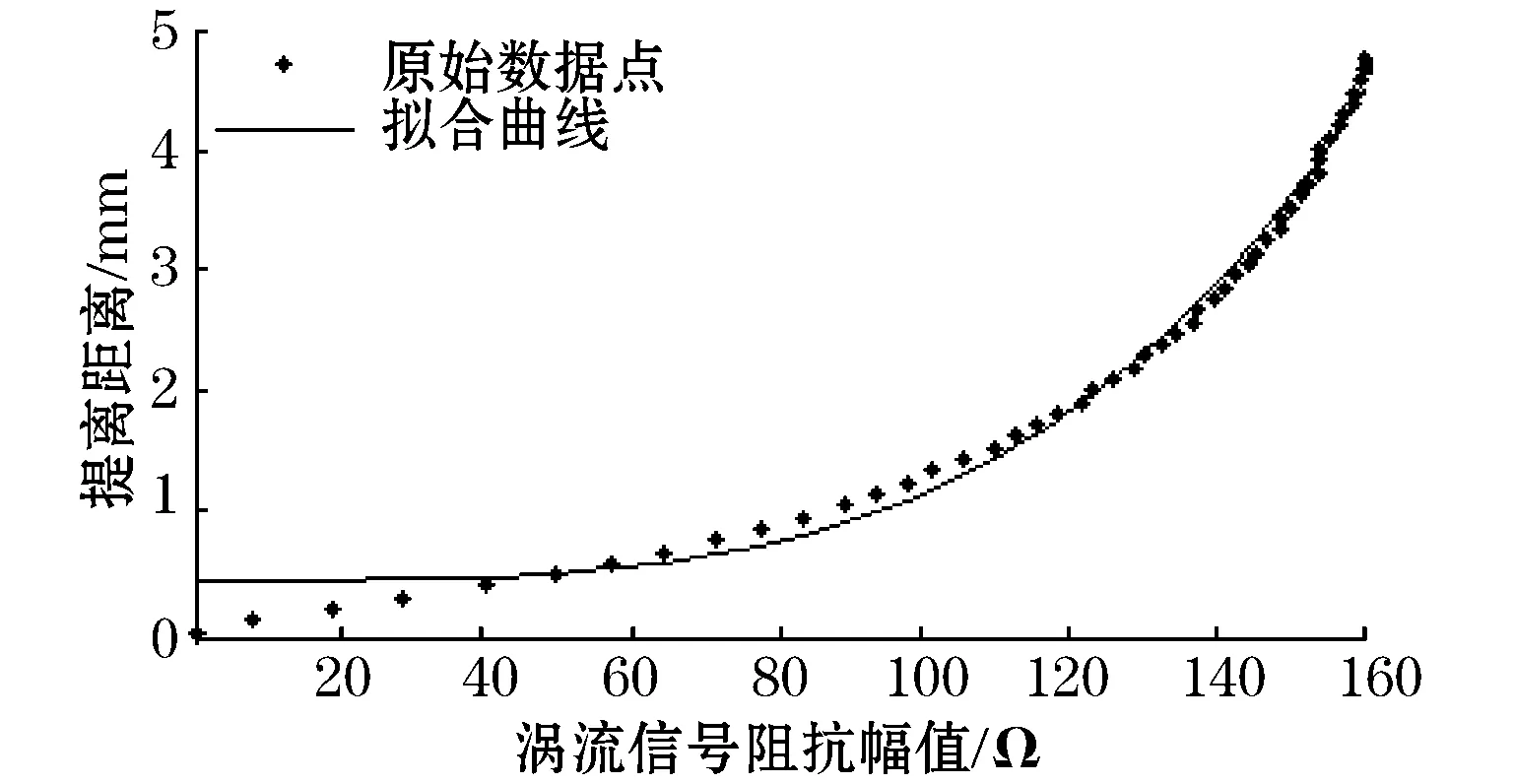
图6　幂函数拟合涡流信号与提离距离

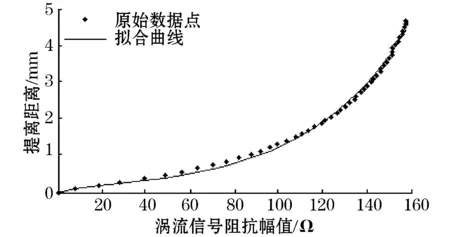
图7　指数拟合涡流信号与提离距离

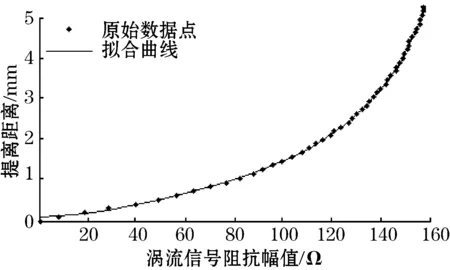
图8　高斯拟合涡流信号与提离距离

对比图5、图6、图7、图8可看出，高斯函数拟合曲线与原始数据吻合性比4次多项式、幂函数和指数函数的都好；拟合数据的误差最小。对4种函数拟合后数据与原始数据的和方差(SSE)、均方根(RMSE)、确定系数(R-square)，以及0～5 mm内的最大误差进行分析(如表1)。

表1　4种拟合方法拟合数据对比表

由表1可以得出，高斯函数拟合数据和原始数据对应点误差的SSE和RMSE小于4次多项式、幂函数和指数函数，而表征模型对数据拟合好坏的R-square却大于4次多项式、幂函数和指数函数。即针对涡流信号与提离距离的标定，4种拟合方法中高斯函数的拟合精度最高，拟合误差最小，拟和模型最好。

3．3多次试验结果

为了更好的应用，同时验证高斯函数对涡流信号与提离距离标定比4次多项式、幂函数和复合指数函数好。在相同条件下，采集5组数据，分别采用4种拟合方法对涡流信号阻抗幅值与提离距离进行标定，对比分析4种拟合数据的SSE、RMSE、R-square，以及0～5 mm内的最大误差(如表2)。

由表2可以看出，在5组数据的4种拟合方法中，高斯拟合的R-square最大，SSE、RMSE和提离误差最小，且提离误差均小于0.089 mm．进一步说明针对涡流信号与提离距离标定，高斯函数是一个理想的标定曲线模型。

4　结论

为提高当前国内涡流测厚仪测量范围，增加厚涂层测量精度，通过对比分析4次多项式、幂函数、复合指数函数和高斯函数对涡流信号与提离距离进行标定，对比分析拟合数据与原始数据的SSE、RMSE、R-square和最大误差，研究提高涡流测厚的标定方法。结果表明，高斯函数拟合较其他拟合方法的提离误差最小，测量精度最高，在0～5 mm提离范围内，误差在0.089 mm，相对于国内大量程时±3%H(即0.15 mm)的提离误差，有了很大提高。通过优化标定曲线的拟合函数可以很大程度地提高涡流测厚的测量范围和测量精度。

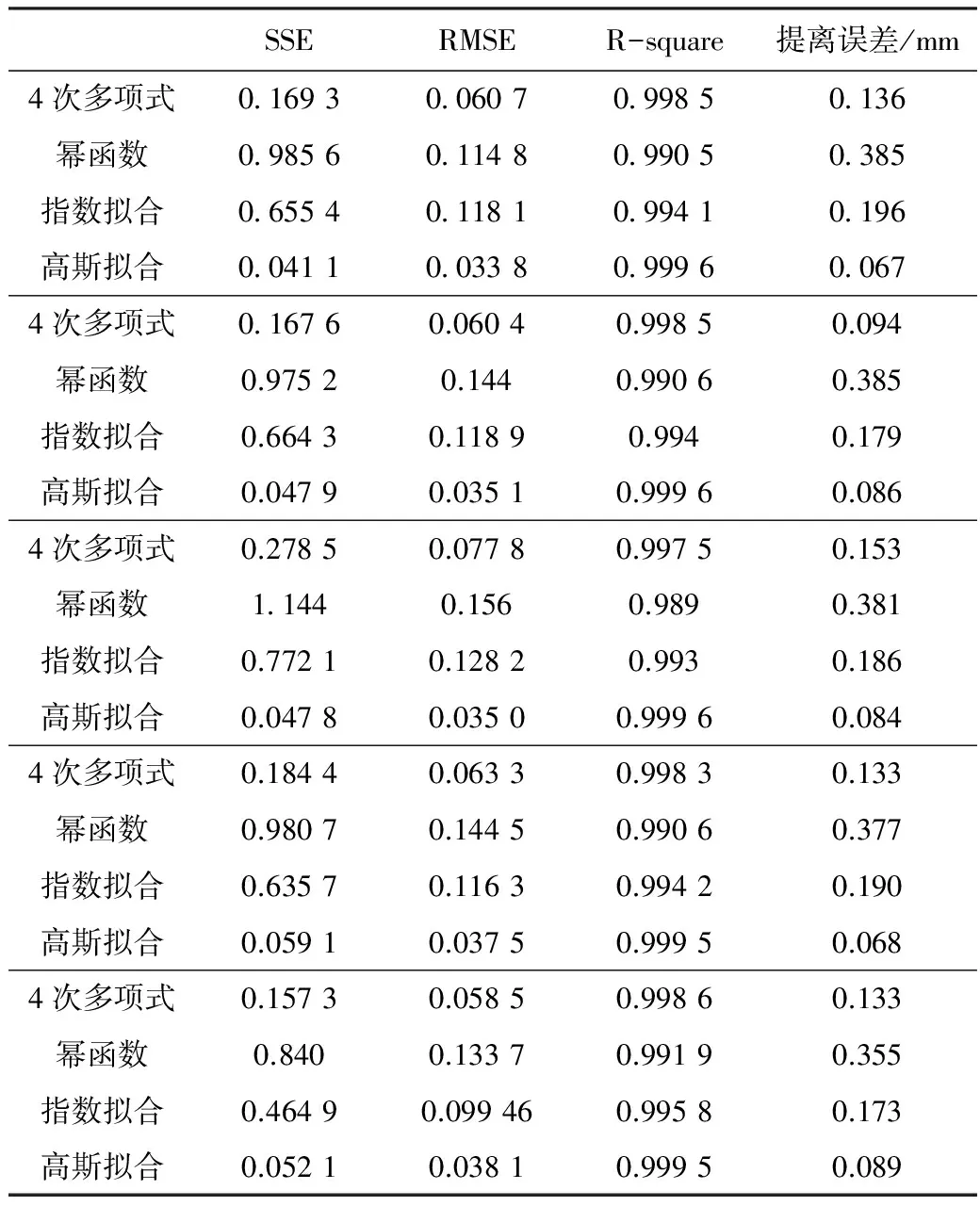
表2　5组数据不同拟合方法对比

参考文献：

[1]刘振作．流涂镀层测厚仪开发与应用．上海涂料．2004，42(3)：34-36．

[2]曾亮，任吉林．特种复合材料涂层厚度涡流法测量技术的研究：[学位论文]．南昌：南昌航空大学，2012．

[3]楼敏珠，张云柯，程庆丽，等．智能高精度涂镀层涡流测厚仪的研制．无损检测．2010，32(6)：434-437．

[4]张会云．金属薄镀层涡流测厚技术研究：[学位论文]．北京：机械科学研究院，2003．

[5]ROPER F．A high-frequency eddy current method for the thickness measurement of thin metallic foils using ferritecore transmission systems．NDT&E International，2000，33(2)：163-165．

[6]李长青，DANON Y．非铁磁性金属薄层涡流测厚法．无损检测．2005，27(9)：454-456．

[7]胡鹏．大量程涡流测距探头的仿真设计．传感器与微系统，2012，31(8)：103-106．

[8]任吉林，林俊明．电磁无损检测．北京：科学出版社．2008：221-285．

[9]张玉华，孙慧贤，罗飞路．涡流探头提离效应的理论分析与实验研究．电机与控制学报，2009，13(2)：197-202．

[10]陆兴旺，王伟杰，潘超．涡流测厚传感器阻抗特性分析．传感器与微系统，2009，28(9)：38-43．

[11]张继龙，甄蜀春，贾鹏，等．实验数据的曲线拟合方法及应用．测试技术学报，2003，17(3)：255-257．