巨型钢框架—拉索支撑体系在水平荷载作用下的破坏性能
王 飞,缪冬冬,朱佳锋,彭小龙
(江苏科技大学土木工程与建筑学院,江苏镇江212003)
随着建筑高度越来越高,控制结构设计的主要因素也从竖向荷载转变为水平荷载.在众多新型高层结构形式中,巨型结构由于其巨大的抗侧刚度及超常规的整体性能越来越受到人们的关注[1-2].文献[3]中研究了巨型钢框架的动力特性,并提出了具体的设计建议.文献[4]中评估了Pushover方法分析带支撑钢框架地震位移时的精度.文献[5]中提出了附加阻尼装置的悬挂式巨型钢框架支撑体系,并进行了模态分析.文献[6]中采用Pushover分析方法研究了巨型钢框架—预应力复合支撑体系在水平荷载下的破坏性能.
在巨型钢框架—预应力复合支撑体系基础上,文献[7]中提出了巨型钢框架—拉索支撑体系,并对该体系典型结构进行了Pushover分析,研究了其抗震性能.巨型钢框架—拉索支撑体系即在巨型钢框架中设置V形预应力拉索,将巨型梁的荷载以轴力形式传递给巨型柱,从而减小梁的跨中弯矩,同时还可适当提高结构抗侧刚度.由于文献[7]中结构有部分构件在规范规定的水平风荷载和地震作用下应力比已超过1,故有必要重新确定构件截面尺寸,使其应力比逼近且不超过1.
为进一步研究巨型钢框架—拉索支撑体系的破坏模式及弹塑性性能,文中在倒三角形分布、均匀分布两种水平加载模式下,对优化后的典型巨型钢框架—拉索支撑结构进行Pushover分析,研究该结构在不同水平加载模式下的破坏机理,考察其抗侧刚度、预应力拉索受力特征、构件塑性铰出现的先后顺序.
1 分析模型
分析采用的典型巨型钢框架—拉索支撑结构平面图如图1a)所示.结构总高216m,共54层,每层高4m.结构每9层设4根巨型立体桁架梁并使其与巨型柱相连,巨型梁高4m,由4根工字形弦杆及竖向、斜向腹杆组成.由于结构对称,为简化取其中一榀进行分析,平面计算模型如图1b)所示巨型柱底和地面固接,底层索和地面铰接,不考虑结构和地基的相互作用.经抗风抗震优化设计后各构件截面尺寸见表1,优化后构件间的相对刚度比基本保持不变.其中,主要钢构件均采用Q345B.

表1 优化后的构件截面尺寸Table1 Optim ized section sizes ofmembers
预应力索的初始拉力取值准则为:“最不利工况下,受压预应力拉索剩余拉力接近零”及“正常使用状态下,巨型梁的变形满足规范要求且不出现反拱”[8-10];各层拉索直径按文献[10]方法确定.各层拉索参数见表2.

图1 结构计算模型Fig.1 Structural com putingmodel

表2 拉索的直径和预拉力Table2 Diameters and pretensions of cables
采用有限元程序SAP2000对结构进行Pushover分析,竖向荷载包括恒荷载和活荷载,水平荷拉索采用屈服强度为1670MPa的钢绞线.载采用倒三角分布和均布两种方式,施加方向自左向右,大小呈线性增长.这是因为倒三角加载得到的是推覆结构推覆曲线下限,均布加载得到的是结构推覆曲线上限,且实施起来比较简单.设定分析类型为静力非线性,并考虑P-Δ效应.预应力拉索和梁柱中构件一样,均采用框架单元,但只受拉,其压拉比限值为0,且定义其截面主惯性矩为一极小值,其预拉力通过降温法施加.塑性铰采用FEMA型,压弯铰(PMM铰)设在巨型柱柱肢两端;弯矩铰(MM铰)设在巨型梁弦杆、楼层梁两端;轴力铰(P铰)设在拉索中间.位移监测点选择模型顶点,监测位移值取4m.
2 分析结果
2.1 结构的破坏模式
倒三角荷载下,底部剪力达到19 081 kN时,第一大层柱间支撑最先开始屈服,其他杆件均保持弹性,结构顶点位移为1712mm;底部剪力达到20844 kN时,第二大层巨型梁腹杆开始出现塑性铰,相应顶点位移为1895mm;底部剪力达到24618kN时,第一大层楼层梁开始出现塑性铰,相应顶点位移为2384mm;底部剪力达到26453 kN时,相应顶点位移达到2670mm,右侧柱肢底部开始出现塑性铰,结构塑性变形继续增大;底部剪力达到27 705 kN时,相应顶点位移达到2 879mm,下部两层楼层梁和柱肢中的塑性铰大量出现,结构达到极限承载状态.
倒三角荷载下,极限承载状态结构塑性铰出现情况如图2所示,其破坏顺序依次为:巨型柱肢间支撑、巨型梁腹杆、楼层梁、柱肢.水平荷载达到极限时,结构体系的塑性发展相当充分,其中巨型梁腹杆,巨型柱肢间支撑和楼层梁的塑性变形程度相当大,形成了为数众多的塑性铰.
结构在均布荷载作用下的出铰情况与倒三角分布荷载相同.
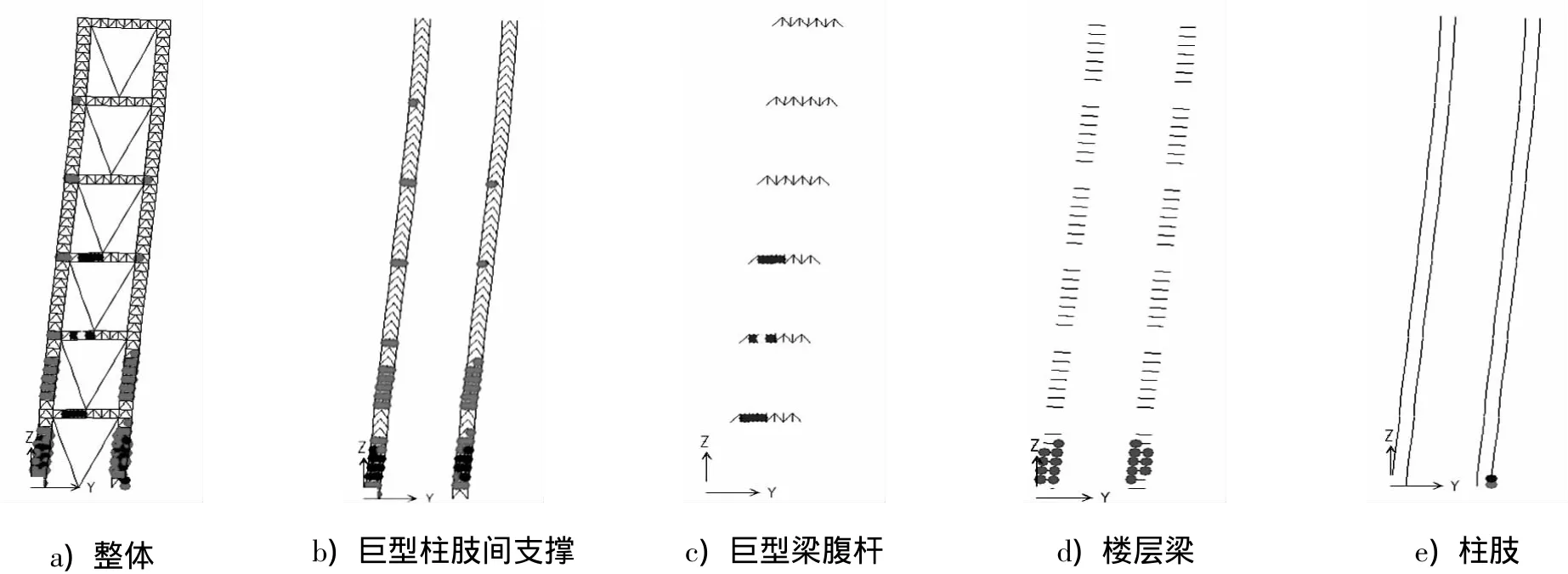
图2 倒三角荷载作用极限状态下结构中的塑性铰Fig.2 Plastic hinges under horizontal ultimate load with inverted triangle distribution
2.2 底部剪力和抗侧刚度
按倒三角和均布两种加载方式分别对巨型钢框架—拉索支撑体系进行静力推覆分析得到的底部剪力F、抗侧刚度K与顶点位移S之间的关系如图3所示.图3a)表明,水平荷载较小时,结构体系基本处于弹性状态,即图中开始的直线部分.随着荷载逐步增大,结构由弹性向塑性状态过渡,底部剪力曲线也从直线段过渡到曲线段,且曲线斜率逐步趋于平缓.最终,在倒三角荷载下,当荷载达到27705 kN,相应顶点位移为2879mm时,结构达到极限状态.在均布荷载下,当荷载达到38 018 kN,相应顶点位移为3109mm时,结构达到极限状态.可见,当顶点位移相同时,均布荷载得到的底部剪力大于倒三角荷载,不同加载方式得到的结构性能曲线也不同.
图3b)表明,水平荷载增加时,结构的水平抗侧刚度逐渐减小.倒三角荷载下推覆得到的结构抗侧刚度小于按均布荷载推覆得到的抗侧刚度,且前者刚度下降比后者趋于平缓.施加倒三角荷载时结构的初始刚度为13.49 kN/mm,施加均布荷载时结构的初始刚度为18.97 kN/mm.
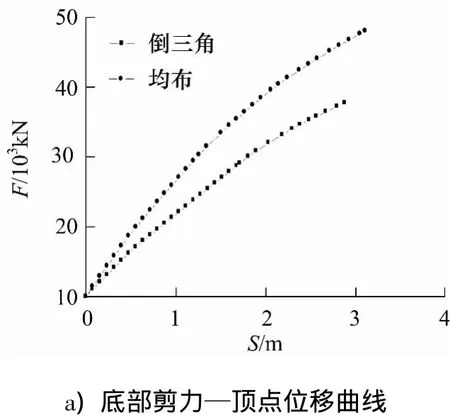

图3 结构底部剪力、抗侧刚度和顶点位移的关系Fig.3 Base shear and lateral stiffness versus roof displacement
为考察拉索的影响,现将无拉索和有拉索两种情况下结构的极限荷载和抗侧刚度对比于表3.由表3可知,倒三角荷载作用下,无拉索的巨型钢框架结构的极限荷载较巨型钢框架—拉索支撑结构降低18.3%,相应的顶点位移增幅为35.8%,结构初始刚度下降5.89 kN/mm,下降幅度达43.7%;均布荷载作用下,巨型钢框架结构极限荷载较巨型钢框架—拉索支撑结构降低21.2%,相应的顶点位移降幅为23.3%,结构初始刚度下降了8.1 kN/mm,下降幅度达到42.7%.这说明拉索的存在有效增强了结构的抗侧刚度,并使结构的侧向承载力得到了大幅提升.

表3 极限状态时结构对应的极限荷载和抗侧刚度Table3 U ltimate load and lateral stiffness in lim it state
2.3 拉索应力
倒三角和均布荷载作用下,拉索应力σ随荷载的变化情况分别如图4,5所示.对比图4,5,可发现在两种不同加载模式下,拉索应力随顶点位移变化的总体趋势相近,如顶层拉索的应力变化速率都缓于其他各层,且顶层拉索退出工作的时间也都晚于其他层,底层拉索应力变化速度随顶部位移增加都会出现一个突变点,等等,但也有些差别.最值得注意的一点是:均布荷载下结构达到极限承载状态时,拉索S1(图1b))的应力为1016.32MPa,仍未屈服;倒三角荷载下结构达到极限承载状态时,S1的应力为1670MPa,已屈服.总得来说,均布荷载下,底部三大层索拉应力所受影响大一些,而倒三角荷载下,顶部三大层索拉应力所受影响更为显著.

图4 倒三角荷载下拉索应力—顶点位移曲线Fig.4 Relationship between prestresses of cables and roof displacements under inverted triangle load

图5 均布荷载下拉索应力—顶点位移曲线Fig.5 Relationship between prestresses of cables and roof displacements under uniform load
3 结论
1 )对巨型钢框架—拉索支撑结构进行静力推覆分析得到倒三角和均布两种加载方式下塑性铰的出现顺序均为:巨型柱肢间支撑、巨型梁腹杆、楼层梁、柱肢,体现了“强柱弱梁”的抗震设计思想.
2 )水平均布荷载作用时巨型钢框架—拉索支撑结构的反应较倒三角荷载作用时更敏感,相应顶点位移也更大.同时,对比无拉索的巨型钢框架结构可知,预应力索大大加强了结构的抗侧刚度,改善了结构的受力性能.
3 )倒三角和均布两种加载方式下,拉索应力随顶点位移的变化总体相似.拉索应力增加的速率越快,同一层中拉索退出工作的时间越早.应特别注意,极限荷载时,均布加载方式下底层拉索已屈服,而在倒三角加载方式下并无拉索屈服.
4 )实际工程设计时,应同时采用均布和倒三角方式这两种实施起来比较简单的加载方式评估结构抗震性能.
References)
[1] 沈祖炎,陈荣毅.巨型结构的应用与发展[J].同济大学学报:自然科学版,2001,29(3):258-262.
Shen Zuyan,Chen Rongyi.Applications and developments ofmega-structures[J].Journal of Tongji University:Natural Science Edition,2001,29(3):258-262.(in Chinese)
[2] 张光辉,程兆君.巨型结构体系的特点及发展趋势[J].中国水运:理论版,2006,4(2):120-121.
Zhang Guanghui,Cheng Zhaojun.Characteristic and development tendency of mega-structure system[J].China Water Transport:Theory Edition,2006,4(2): 120-121.(in Chinese)
[3] 舒赣平,张宇峰,吕志涛,等.巨型框架结构的动力性能研究及设计建议[J].土木工程学报,2003,36 (2):41-45.
Su Ganping,Zhang Yufeng,Lv Zhitao,et al.Shaking table test onmegaframemodel and some design advices[J].China Civil Engineering Journal,2003,36(2):41-45.(in Chinese)
[4] Moghaddam H,Hajirasouliha I.An investigation on the accuracy of pushover analysis for estimating the seismic deformation of braced steel frames[J].Journal of Con-structional Steel Research,2006,62(4):343-351.
[5] 唐柏鉴,阮含婷.附加阻尼装置的悬挂式巨型钢框架支撑体系模态分析[J].江苏科技大学学报:自然科学版,2008,22(4):18-23.
Tang Baijian,Ruan Hanting.Modal analysis of megaframe-brace-suspended structurewith damper[J].Journal of Jiangsu University of Science and Technology: Natural Science Edition,2008,22(4):18-23.(in Chinese)
[6] 邵建华,唐柏鉴.巨型钢框架—预应力复合支撑体系在水平荷载作用下的破坏性能[J].建筑科学,2012,28(5):9-14.
Shao Jianhua,Tang Baijian.Mechanical performance of mega steel frame-prestressed composite bracing structure under horizontal loads[J].Building Science,2012,28 (5):9-14.(in Chinese)
[7] 唐柏鉴,彭小龙,邵建华.巨型钢框架—拉索支撑体系的Pushover分析[J].工业建筑,2013,43(3):120-124.
Tang Baijian,Peng Xiaolong,Shao Jianhua.The pushover analysis ofmega steel frame-cable bracing structure[J].Industrial Construction,2013,43(3):120-124.(in Chinese)
[8] 顾盛,唐柏鉴.多层预应力巨型支撑—钢框架结构拉索初拉力预估研究[J].工业建筑,2011,41(1):120-123.
Gu Sheng,Tang Baijian.Estimation of initial tension of cables in multi-storey prestress-mega-braced steel frame structure[J].Industrial Construction,2011,41(1): 120-123.(in Chinese)
[9] 唐柏鉴,顾盛.巨型钢框架复合支撑体系的拉索预拉力预估理论[J].解放军理工大学学报:自然科学版,2012,13(6):651-657.
Tang Baijian,Gu Sheng.Determination theory on cable initial pre-stress of mega steel frame and pre-stressed composite brace structure[J].Journalof PLAUniversity of Science and Technology:Natural Science Edition,2012,13(6):651-657.(in Chinese)
[10] 马珺,唐柏鉴.巨型钢框架—拉索吊挂结构拉索参数确定方法[J].力学与实践,2012,34(6):23-26.
Ma Jun,Tang Baijian.Estimation of cable's parameters inmega steel frame and cable hanging structure[J].Mechanics and Engineering,2012,34(6):23-26.(in Chinese)

