高斯界面反射超声散斑场的数字模拟

郑伟花，贾 虎

(南阳师范学院土木建筑工程学院，河南南阳473061)

超声入射粗糙的表面或在非均匀介质内传播时，散射波会在界面反射空间或介质空间中产生干涉，形成散斑.和人们认识激光散斑的过程相似，一直以来人们将散斑作为噪声来抑制，随着对超声散斑和运动规律研究的进展［1－2］，人们开始意识到散斑也是信息的载体，可以反应物质的信息和变化，由此产生了超声散斑相关法测量位移，以及利用散斑本身所带信息测量界面的应变等各种测量方法［3－4］.自从1997年，文献［5］类比激光散斑干涉检测的原理和方法，提出了建立超声散斑干涉检测新技术的思想之后，国内一些学者对超声散斑检测也有了进一步的相关研究的报道，但是国外一直未见相关报道.

这些测量方法虽然理论上较为先进，但是测量误差都不容忽视，多数在5%以上，有的甚至20%多，究其原因主要是因为超声散斑在实验测量中接收比较困难，需要逐点接收信号，整个散斑图不是同一时刻接收，再加上处理过程中仪器本身也存在噪声，这也是超声测量技术一直没有像激光测量技术那样迅速发展的原因之一.但是超声具有穿透能力，可以对内部物质进行检测的这些优点，使其比激光更有前途.

文中针对超声散斑测量技术中所存在的问题，提出采用数字模拟的方法来形成散斑场，可以有效地避免实验过程中由于噪声或者人工操作所带来的测量误差.文中以散斑声强为研究对象进行数字模拟，并对模拟的散斑强度分布图结果进行实验验证.

1 理论分析

在粗糙界面的均值平面上建立坐标系O0－x0y0，波长为λ的超声波辐照在界面上，辐照区域为D0.在散射空间中与界面相平行的某一观察面上建立直角坐标系O－xy，其上任一观察点P的坐标为(x，y)，两直角坐标系平行，相距为Z，如图1.

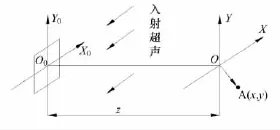
图1 超声传播示意Fig.1 Schematic diagram of ultrasonic transm ission

在观察面上任一点(x，y)上超声散斑的复振幅等于:

式(1)中，h(x，y;x0，y0)为空间传播权函数，它由超声传播过程确定，与反射界面的粗糙度无关，在夫琅禾费近似条件下［1］，有

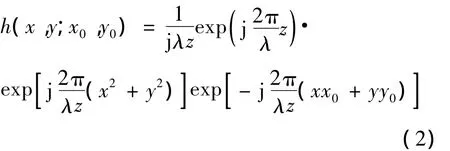
式(1)中，A0(x0，y0)为散射基元d x0d y0散射超声的复振幅，各个基元具有相同的振幅和相位，在统计上相互独立.界面对入射超声的扰动相当于对其相位进行随机调制，而不改变振幅.这样当振幅为A0的超声均匀地辐照在粗糙界面上时，A0(x0，y0)的表达式为:

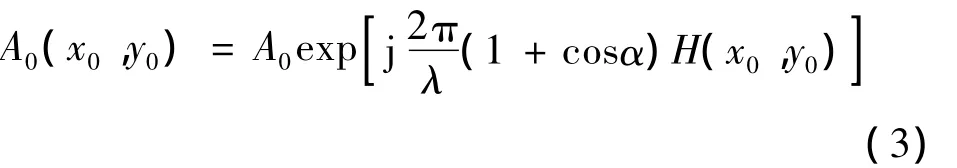
式(3)中α为超声的入射角;H(x0，y0)为粗糙界面的高度函数;A0为入射超声的振幅.

1.1 高斯粗糙界面的构造

随机表面的模拟生成是将表面高度函数H(x0，y0)用空间高度的点序列来表示，采用滑动平均法产生空间高度的点序列［6］.

首先生成(2M+1)个统计无关的随机数vi(i=－M，－M+1，…，0，…，M－1，M)其满足正态分布条件，均值为零，方差为σ.

其次用(2N+1)个权重系数wj对上面生成的随机数vi进行滑动平均，

得到(2M－2N+1)个随机数zn(n=N－M，N－M +1，…0，…M－N－1，M－N)，此随机序列满足预先指定的统计特性:均方根粗糙度为σ，相关长度为T.显然{zn}代表了想要的数值表面.

实现上述目标的关键是合理选择权重系数wj，并确定M和N的具体数值.如果定义自相关函数为

式(4)中，t为正整数，zn+t的表达式为

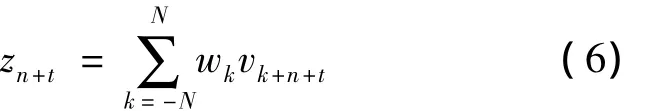
由文献［6］可知

式(7)中，F为傅里叶变换，F－1为傅里叶逆变换，式(7)给出了权重函数和自相关函数间的对应关系.

假设随机表面的高度函数为h(x)，相邻离散高度点的间隔为Δx，根据高斯相关的概念，令tΔx=(x－x')有:

对式(8)变量代换，以t为变量，两边进行傅里叶变换，然后开方，再进行傅里叶逆变换，得到:

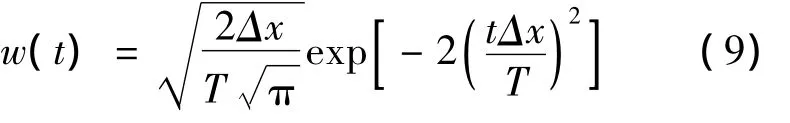
式(9)即为权重函数的求解表达式.序列可用下式求解:

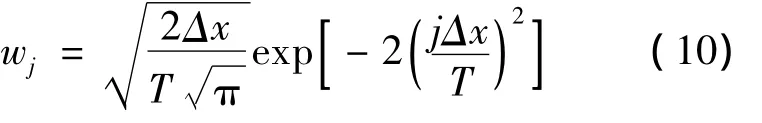
一般来说，只要wj不等于零就满足要求，按照这个要求，假设j≥N并取j=N，wj≈0，可解得

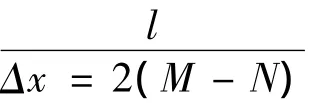
利用上面的步骤可以使用计算机生成符合预定特性的随机表面，生成的高斯粗糙界面是在x方向上正态分布，在y方向上为均匀分布.形成的点序列组合而成的高斯界面高度方阵为{z(xi，yj)}2M－2N+1.文中暂不考虑两个方向上正态分布的高斯随机表面.

1.2 散斑场的数值模拟

不考虑随机表面不同高度点间的相互遮蔽效应及多重散射作用，将式(2)，(3)代入式(1):

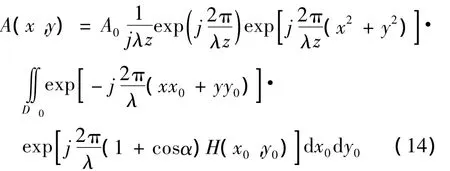
欲将式(14)离散化，其中H(x0，y0)可取{z(xi，yj)}2M－2N+1，若被积函数记为B1(x0，y0)，积分号外的因子记为B2(x，y)，则可记为

二重积分中利用长方体代替曲面的柱体，可将上述积分离散化为

式(16)中B1(xi，yj)可表达为

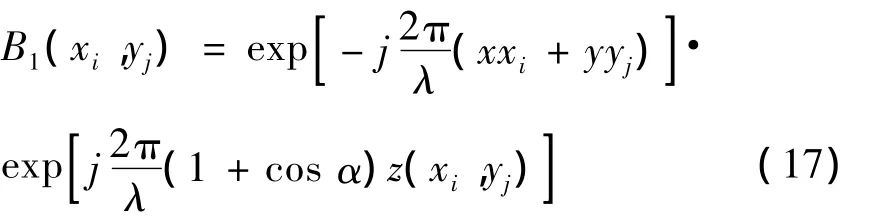
取Δxi=Δyj=Δx为常数.

图1中观察平面的离散化间距可以任意取，如果想要观察面的散斑信号比较密集可以取小一点，如果不需要很密集离散间距可以取的大一些.这样离散化公式(16)可以写成

利用式(18)计算观察面任意点处的复振幅，取其模则得到该点的声强.利用光滑表面在观察平面原点处的声强对式(18)进行标准化，可使得计算结果较为简单，也不失原来特性.

1.3 散斑场的数值模拟结果

考虑到超声波长以及散射条件，按照上述方法，取T=0.5mm，Δx=0.02mm，σz=2μm，入射角α=60°.超声振幅A0取200，相当于脉冲信号发射器的档位调到中档，超声辐照区域为正方形边长L=20mm，在z=20mm和40mm的2个观察面上取256×256个计算点，区域大小为2.56 cm×2.56 cm.计算模拟的结果如图2.

图2 超声散斑计算机模拟Fig.2 Computer simulation of ultrasonic speck le field

2 实验

2.1 实验系统

超声散斑采集与激光散斑的采集不同，不是用CCD摄像头一次性拍摄下来，而是用超声聚焦探头逐点采集，输入微机经过傅里叶变换，提取出每个点中心频率的幅度作为特征值，形成整个散斑场.所以采集超声散斑场的数据工作量很大，因此将无限区域的散斑场划成有限区域来采集.为了验证计算机模拟的散斑场的正确性，实验中各项参数依然保持计算机模拟时采用的参数.为了避免超声在空气中传播衰减很快的缺点，选择实验在水中进行，接收与发射的探头都采用水浸探头.

如图3，采集区域和计算机模拟时一样，在距离辐照面20mm和40mm的位置，将区域划分为256×256个点.聚焦探头由步进电机带动，沿(x，y)个方向上移动采集数据.T，R分别为发射探头和接收探头.

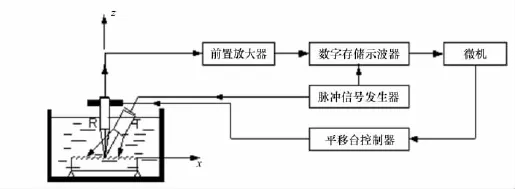
图3 实验系统Fig.3 Experimental system

产生粗糙界面的试件是平面研磨标准试样，为了避免误差，其尺寸与辐照面一样为边长L=20 mm的正方形，用表面轮廓仪测得其表面粗糙度Ra=2μm，属于一般的加工表面，不需精加工可以达到这个要求.经过研磨的标准试样符合理论推导中假设的高斯高度分布［7－8］.超声波长较大，此试件的粗糙度能使超声在反射界面空间发生散射，但不属于强散射范围，属于弱散射的范围.实验结果如图4a)，b).

图4 超声散斑场实验结果Fig.4 Ultrasonic speck le field experimental results

2.2 结果讨论

纵向对比图2a)和图4a)，两个结果都符合散斑场的特性暗区多亮点少，并且强度范围也相似，都在0～250之间，这并不能说明他们的强度是一样的，因为实验结果明显要比计算机模拟结果在均值上低很多(从灰度上看更暗).图2b)和图4b)也具有这种特征.经过计算，图2a)均值比图4a)均值低50左右，方差也大4.32，并且图2a)是用光滑界面的散射中心点的幅值标准化过的，所以在数值上缩小了范围，实际两图数值差距要大于50.图2b)比图4b)均值低40左右，方差大3.92.横向对比图2a)和2b)，观察面距离散射面越远，散斑场的强度越低，这符合实验中因超声在传播过程中的能量损失而造成的强度降低情况.

经过计算，图2a)与图4a)中亮点超过200的个数是不一样，图2a)比图4a)要多近20个;图2b)与图4b)中亮点超过200的个数也不一样的，图2b)比图4b)要多25个.计算机模拟的散斑场具有更多可以研究的散斑点，因为一般散斑点越暗，被掩盖的有用信息就越多.在实验中由于仪器噪声的存在会掩盖很多强度较低的散斑颗粒，而实验所得的散斑图中散斑颗粒少，正说明计算模拟所得的散斑场要比实验所得的数据含信息量更多.

图2与图4相比，散斑颗粒分布并不完全相符，并具有随机性，有的区域多有的区域少，这是因为模拟产生和实验中的散射表面虽然都符合高斯分布，但是每个位置的表面高度并不完全相同，只能从统计意义上来看模拟结果和实验结果是否具有相似性，例如亮区和暗区的多少，均值和方差等等.

根据文献［6］可知，界面上声场复振幅相位的方差与界面高度变量的方差有严格的数学关系，可以根据散斑图，采用理论推导的反计算方法得到界面高度变量的方差，从而计算出界面的粗糙度，这为散斑测量又提出了一条新的思路.

超声散斑场的计算机模拟只是作者沿着模拟这个方向研究的第一步，这个方向还有很多课题值得去研究，例如不同的入射角，不同的粗糙度以及不同的相关长度对测量散斑场有何影响，这些课题在实验中是很难实现的，尤其是实时改变超声入射角度测量是比较困难的，有了计算机模拟的方法，这些方法就可以实现.

3 结论

文中旨在得到更为精确的超声散斑场，以及克服超声散斑实验中的各种仪器噪声和人工操作产生的误差，提出了用计算机模拟产生散斑场.通过理论推导及计算模拟，模拟产生了高斯随机相关表面，并在该类界面上产生了散斑场.为了进一步对比计算机模拟与实验得到的散斑场的区别，建立了实验系统，得到了实验散斑场，通过对比发现计算机模拟得到散斑场比实验得到的散斑场强度更大，散斑颗粒更多，对比度更好，携带更多的有用信息.

References)

［1］ 吴艳阳，朱鸿茂，王寅观.高斯界面背向散射超声散斑复振幅统计特性［J］.声学学报，2004，29(3):249－253.

Wu Yanyang，Zhu Hongmao，Wang Yinguan.Statistical properties of complex amplitude of ultrasonic speckles back scattered from a Gaussian interface［J］.Acta Acustica，2004，29(3):249－253.(in Chinese)

［2］ 朱鸿茂，郑伟花，黄忠文，等.运动界面上反射超声散斑空间运动的研究［J］.物理学报，2004，53(8): 2614－2620.

Zhu Hongmao，Zheng Weihua，Huang Zhongwen，et al.Research on spatialmotion of ultrasonic speckles backscattered from an interface inmotion.［J］.Acta Physica Sinica，2004，53(8):2614－2620.(in Chinese)

［3］ 郑伟花，朱鸿茂.超声散斑数字干涉法测量物体位移的研究［J］.力学与实践，2008，30(1):75－78.

Zheng Weihua，Zhu Hongmao.Displacement measurement by ultrasonic speckle digital interferometry［J］.Mechanics in Engineering，2008，30(1):75－78.(in Chinese)

［4］ 褚俊，沈磊，罗志华，等.应用超声散斑相关法测量水下物内层界面位移［J］.应用力学学报，2012，29 (4):406－420.

Chu Jun，Shen Lei，Luo Zhihua，et al.The displacementmeasurement of inner surface of an object in water using ultrasonic speckle correlationmethod［J］.Chinese Journal of Applied Mechanics，2012，29(4):406－420.(in Chinese)

［5］ Hong Z K，Han JB.Consideration on speckle pattern interferometry of ultrasonic speckles［J］.Ultrasonics，1997，35(4):329－332.

［6］ 高昭.基于空间平均静态及动态散斑法表面粗糙度测量技术研究［D］.哈尔滨:哈尔滨工业大学，2009: 55－63.

［7］ Tanner L H.The use of laser light in the study ofmetal surfaces.［J］.Optics and Laser Technology，1976，8:113－116.

［8］ Silvennoinen R，Peiponen K E，Asakura T，etal.Specular reflectance of cold-rolled aluminum surfaces.［J］.Optics and Lasers in Engineering，1992，17:103－109.

［9］ 郑伟花，朱鸿茂，贾虎.超声散斑相关法测量转角的相关性研究［J］.应用声学，2010，29(2):141－147.

Zheng Weihua，Zhu Hongmao，Jia Hu.Correlation of rotating angle measurement by the ultrasonic speckle correlation method［J］.Applied Acoustics，2010，29(2): 141－147.(in Chinese)