基于均值-CVaR的供应链协调保险契约机制

杨兴林，朱陈陈

(江苏科技大学经济管理学院，江苏镇江212003)

供应链网络通常是由供应商、制造商、分销商、零售商以及顾客组成，而各成员之间的合作与协调一直是供应链管理的研究重点.传统的供应链决策者被假定是风险中性的，以期望利润最大化或成本最小化为目标，然而由于市场需求的随机性，决策者对待风险的不同态度决定了不同的生产或库存计划，如何设计有效的契约来协调考虑企业成员风险态度下的供应链，逐渐成为供应链契约研究的新热点.

近年来，国内外学者开始对具有风险规避特性的供应链协调及契约机制进行探讨，并使用不同的方法来刻画决策者的风险态度.例如，文献［1－2］首次用群体决策理论对具有风险规避特性的供应链协调进行了定义，并证明了传统的批发价格契约，回购契约以及收益共享契约难以协调风险中性的供应商和下游风险厌恶(downside-risk-averse)的分销商组成的供应链系统，同时给出了能够协调此种情形下的风险共享契约.文献［3］用效用函数(utility function，UF)理论得出了风险规避的零售商在经典契约下最优订货量都小于中性时的订货量结论.在决策方法方面，文献［4］用均值方差(mean-variance，MV)的方法证明了保险契约能够协调成员都有风险规避倾向的供应链.文献［5］在文献［4］的基础上设计出零售商风险偏好参数未知的组合保险契约模式.另外，文献［6］在条件风险均值(conditional value-at-risk，CVaR)准则下传统契约通过改变契约参数也能达到供应链的协调以及文献［7］基于CVaR的风险度量方法对电力储备领域设计出供应链模型，并针对不同的风险规避态度提出两种协调策略.总体而言，上述传统的风险度量方法对具有风险规避特性的决策者能够很好地刻画，但难以掩饰其存在的缺陷.如效用函数在度量目标函数时比较繁琐，而MV的方法是对称的处理收益和损失，不能很好地刻画风险.CVaR虽然能克服上述缺点，但只关注下游风险的损失，决策目标太过保守.所以为了弥补CVaR的不足，采用权衡收益和风险损失的均值-CVaR方法可以更好地度量决策者的目标函数.

其实，国外已有一些学者将均值-CVaR应用到供应链决策模型当中.例如，文献［8－9］将均值-CVaR首次应用到供应链库存模型之中，分析了是否考虑缺货损失两种供应链最优订货决策.文献［10］通过使用均值-CVaR准则，发现套头交易策略能够提高订货量以及期望利润和下游风险利润.文献［11］用均值-CVaR度量准则研究了带有现货市场的报童模型问题.

上述文献都是研究均值-CVaR度量准则下的供应链库存问题，而此种情形下供应链协调机制研究还非常缺乏.文中在均值-CVaR度量准则下，建立了具有风险规避特性的零售商决策目标函数，重点考察固定的批发价格契约以及传统的保险契约对风险中性供应商与风险规避零售商组成的供应链系统协调机制的影响，旨在提出能够达到供应链完美协调的调整后的保险契约机制.

1 基本描述

1.1 CVaR与均值-CVaR的定义

1.1.1 条件风险估值

条件风险估值具有良好的计算特性，它是测量期望利润低于分位水平的利润分布，被广泛的应用于金融和保险领域.其定义为［12］:

式中:η为决策者的风险规避程度，范围为［0，1］，η越小表明决策者越厌恶风险，取1说明决策者不具有风险特性;g(y，x)为决策者的决策行为y(固定值)和x(随机变量)下的利润函数;f(x)为概率密度函数;qη为随机变量x的η分位数，即

为了便于计算，条件风险估值还有更一般的等价表达式:

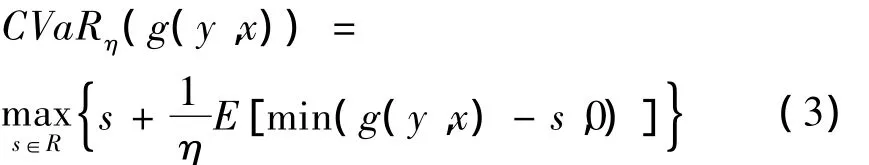
1.1.2 均值-CVaR

由于CVaR着重的是下游风险的测量，利润低于分位数的平均利润，这样决策者的决策目标太过于保守，所以把决策目标定为CVaR利润和期望利润的权衡值是比较客观的.此处定义的均值-CVaR为期望利润和 CVaR的凹组合，公式可表述如下［8－9］:

式中:E［g(y，x)］为风险中性时的期望利润; CVaRη(g(y，x))为CVaR风险度量准则下的利润; Gη(g(y，x))为均值-CVaR的决策目标利润，即权衡绩效.λ为权衡比重，范围λ∈［0，1］，当λ=1，表明决策者不具有风险特性，只考虑期望利润;当λ＜1，决策目标考虑了风险规避行为，对期望和风险进行了很好的权衡;当λ=0，决策者只看重下游风险利润，即条件风险估值.

1.2 问题描述

文中讨论一个风险中性供应商和一个风险厌恶的零售商组成的两级供应链系统，销售单周期短寿命产品，零售商风险下的绩效用均值-CVaR标准进行衡量.供应商作为Stackelberg博弈的领导者，零售商为追随者，整个供应链信息是透明的.供应商向零售商提供一种合同，零售商在风险水平η下最大化自己的权衡绩效(均值-CVaR)来选择最优订货量.风险中性的供应商设计一个合同来刺激零售商订货，使得整个供应链的渠道期望利润最大，也就是风险中性条件下整个供应链的最优订货量，同时各自选择后的期望利润不低于选择前的期望利润.文中按照文献［2］给出的风险偏好情形下供应链协调的定义，满足下面3个条件可以认为供应链达到了协调状态:①零售商的权衡风险限制能够满足;②整个供应链的渠道利润达到最大化;③零售商和供应商采用契约后的各自收益不小于未采用契约前的收益.

零售商面临随机的市场需求D，其概率密度和分布函数分别为f(x)及F(x)，且F(x)为可微的单调递增函数，F(0)=0.供应商的单位生产成本为c，给零售商的单位批发价格为w且为固定值，零售商销售给顾客的单位价格为p，q为零售商的订货量.销售季节过后零售商未销售出去的单位产品残值为v，且不存在缺货成本或由于缺货而带来的任何损失.其中v，w，p，c均为外生变量，且满足关系:p＞w＞c＞v，Π表示随机利润，E［.］表示期望，r表示零售商，s表示供应商，sc表示整个供应链，i表示保险契约.

根据上面的定义及假定在零售商订货量为q时，零售商的随机利润:

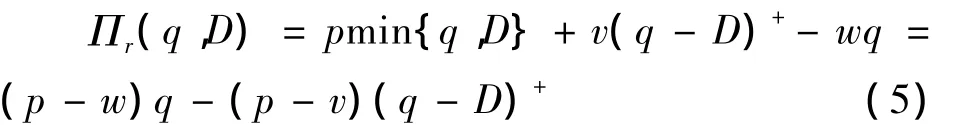
供应商的随机利润:

整个供应链的随机利润:

其中x+=max{x，0}，很容易知道当零售商对待风险的态度为中性时，集中决策下整个供应链的最优订货量可表示为:

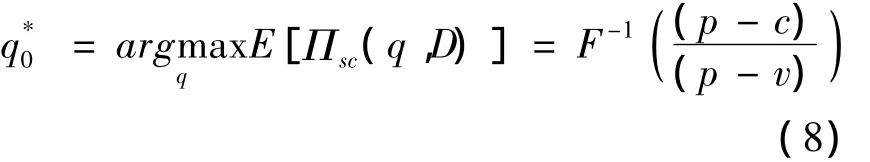
2 基于均值-CVaR的供应链决策与协调

2.1 批发价格契约下均值-CVaR决策模型

零售商在做出最优决策时不仅考虑期望利润，还关注存在的风险.所以零售商以最大化其权衡绩效，也就是均值-CVaR风险度量的决策目标.根据均值-CVaR的定义以及零售商的随机利润，可知均值-CVaR风险决策准则下，零售商的权衡绩效(目标)由公式(4，5)得:

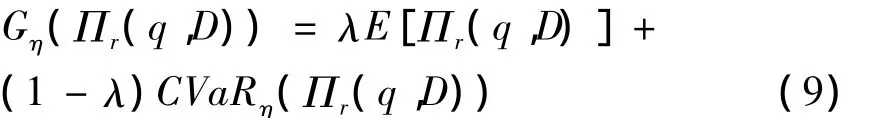
当λ=1，式(9)表示经典的风险中性报童模型;当λ=0，表示报童只最大化下游风险利润CVaRη;当0＜λ＜1，目标函数描述了零售商的风险规避行为，它是刻画两种标准重要性水平.对于风险规避的零售商来说，在均值-CVaR风险度量准则下，最大化权衡目标，即:

此时公式(10)给出的决策目标就表示均值-CVaR风险度量准则下的最优库存决策问题，零售商此时的最优订货量可由文献［9］类似给出.

定理1 批发价格契约下，零售商最大化权衡绩效的最优订货量为

推论1 固定批发价格下，最优订货量是权衡比重和风险规避程度的增函数且小于风险中性时整个供应链的最优订货量.

证明:1)从订货量的表达式可以看出，在权衡比重λ∈［0，1］范围内，F(q)都是随着λ的增大而增大的.根据分布函数是增函数性质，可知最优订货量是权衡比重的增函数.

2 )对于风险规避程度，由公式(11)可以看出，当η比较小时订货量不随着η的变化而变化，成直线状态，当η比较大，大于F(q)时，F(q)是随着η的增大而增大，综合考虑可知订货量也是风险规避程度的递增函数.

3 )为方便起见定义第一个括号内代数式为A，第二个为B.当0≤η＜F(q)时，把A分解得到c)/(p－v).当风险规避程度大于F(q)时，可令L(λ)=η/［1－λ(1－η)］，很容易看出L(λ)是权衡比重的递增函数，且L(0)=η，L(1)=1，B＜ (p－w)/(p－v)＜(p－c)/(p－v)，综上得q小于q.

零售商在权衡绩效目标决策下做出最优订货，此时零售商的期望利润为:

风险中性的供应商在固定批发价格和零售商做出最优的订货决策下，期望利润为:

推论2 零售商和供应商的期望利润是权衡比重和风险规避程度的增函数.

2 )对于供应商而言，供应商给予零售商固定的批发价格，只要零售商的订货量增加，其利润也相应增加.从订货量的分析可知，供应商的期望利润也是权衡系数与风险规避系数的增函数.

由式(11)可以看出，普通的批发价格契约无法使零售商的最优订货量达到供应链的最优订货量，也就是无法实现供应链的协调.引入最近兴起的保险契约机制，来探究供应链的协调情况.

2.2 保险契约下均值-CVaR决策模型

按照文献［4］给出的保险契约机制，此处供应链保险契约是这样定义的:在随机的市场需求下，零售商面临缺货损失，供应商在固定的批发价格下，向零售商提供保险契约.在该契约下，零售商只需承担α倍的缺货损失，供应商承担1－α倍的缺货损失，但零售商必须向供应商提供保费T(可以为负)作为补偿.故保险契约机制下，节点企业的随机利润可表示为

零售商的随机利润:

供应商的随机利润:

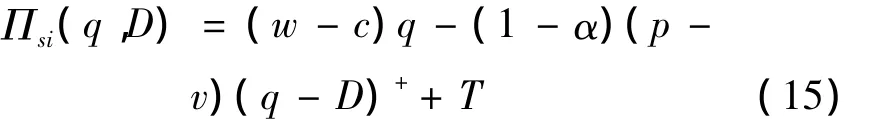
在均值-CVaR度量准则下零售商最大化决策目标为:

由式(14，16)可得保险契约下零售商的最优订货量.

定理2 在固定的批发价格下，供应商提供的保险契约参数α满足:α∈((p－c)/(p－v)，1)时，零售商最大化权衡绩效的最优订货量为

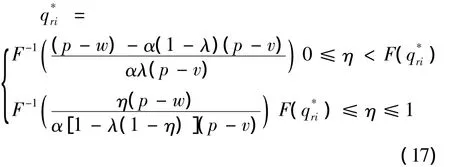
推论3 保险契约下，最优订货量是保险参数α的减函数.

证明:对于任意固定的权衡系数，在满足［0， 1］的范围下，当风险规避系数小于F(q)时，最优订货量对 α求一阶导数有 ∂q/∂α=－(pw)/［α2λ(p－v)f(q)］;当风险规避系数大于F(q)时，∂q/∂α=－η(p－w)/［α2(1－λ(1－ η))(p－v)f(q)］.容易知道不管规避系数范围如何，一阶导数都是小于0的，故最优订货量是保险参数α的减函数，且当α取1时，订货量取最小值，即普通批发价格契约下零售商的最优订货量.也就是说采用保险契约后零售商的最优订货量是不小于批发价格契约下的最优订货量.

推论4 传统的保险契约不能协调具有风险规避特性成员组成的供应链;

从推论4可知，传统的保险契约是无法协调供应链的.若想实现供应链的协调必须对保险参数重新的定义.

2.3 保险契约对供应链的协调机制

零售商接受保险契约后，最大化权衡绩效目标，此时零售商的期望利润为:

风险中性的供应商在固定批发价格和零售商做出最优的订货决策下，期望利润为:

这只是满足了协调条件的第一条，即满足零售商的权衡绩效.如要实现整个供应链的渠道利润最大，可以令q=q，由公式(8，17)得

定理3 能够协调供应链的保险契约参数应满足的关系为:

由定理3容易得出推论(5).

推论5 协调状态下的保险契约参数α，且满足范围α∈((p－c)/(p－v)，1］时，α是权衡比重和风险规避程度η的递增函数.

同时为了激励零售商接受此保险合同，满足协调的第三个条件，保险前后的期望利润需满足以下条件:

把式(12，13，18，19)带入式(21)得:

式中:保费的最大值Tmax=(p－w)(q－q)+(p－vF(x)d x－α(p－vF(x)d x，保费的最小值Tmin=(w－c)(q－q)+(1－α)(pvF(x)d x.

3 数值分析

文中将通过算例，用Matlab7.0软件来分析最优订货量以及保险契约前后利润的变化(图1～6).

假设有关产品的参数设置如下:市场需求服从［1000，2000］的均匀分布，单位产品的零售价格p= 10，供应商给予零售商的固定批发价格w=5，产品的单位成本c=4，产品滞货的情形下单位残值v=3.为了能体现零售商风险规避程度，假设权衡两个标准的权重分别设为:λ1=0.4，λ2=0.5，λ3=0.6.

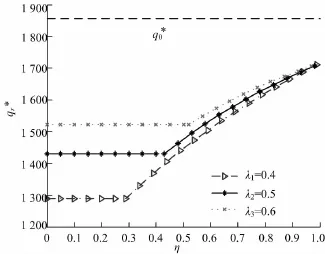
图1 η与λ对零售商最优订货量影响Fig.1 Optimal order quantity as a function ofηfor different values ofλ

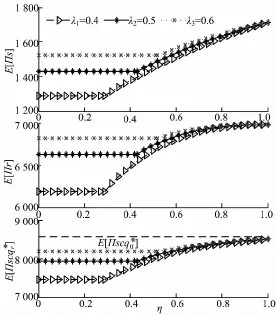
图2 η与λ对供应商、零售商及供应链期望利润影响Fig.2 Profit as a function ofηfor different values ofλ

图3 η与λ对保险参数α的影响Fig.3 Parameter of insurance contract as a function ofηfor different values ofλ

图4 η与λ对保费T的影响Fig.4 Range of prem ium as a function ofηfor different values ofλ

图5 η与T对零售商期望利润的影响Fig.5 Retailer's profit as a function ofηfor different values of T

图6 η与T对供应商期望利润的影响Fig.6 Supp lier's profit as a function ofηfor different values of T

1 )批发价格契约下，零售商的权衡比重和风险规避程度对零售商的最优订货量以及最优订货量下供应链上企业的期望利润的影响.

由图1可以看出零售商的最优订货量是随着权衡系数的增大而增大，也就是零售商越不注重风险，订货量越大;随着规避程度η的增大而增大，也就是零售商越害怕风险(η越小)，其最优订货量越小.当η=1也就是风险中性条件下，最优订货量达到最大，但还是小于整个供应链的最优订货量.这与推论1相吻合的.

由图2可以看出在固定的批发价格下，零售商、供应商以及整个供应链的期望利润都随着风险规避程度η和权衡比重λ的增大而增大.也就是零售商越害怕风险，越注重风险导致订货量减少，从而影响供应商零售商以及整个供应链的收益.零售商的收益对风险规避程度η更敏感.

2 )保险契约下，零售商的权衡比重和风险规避程度对保费参数的影响

由图3可以看出供应商给零售商提供保险合同，为了刺激零售商多订货，达到整个供应链的最优订货量，零售商必须承担一定比例的缺货损失，且随着η的减小而减小，随着λ的增大而增大.也就是说零售商越害怕风险，愿意承担的损失就越小;越不注重风险，订货量越大，可能遭受的滞货损失也就越大，供应商制定的保险参数α也就越大.这与推论5相吻合.

由图4可以看出，供应商给零售商提供的保费范围随着η的增大而逐渐减少，当η＜F(q)时，保费范围对风险规避程度变化比较敏感，且随着权衡比重的增大范围也就越小;当η＞F(q)时，权衡比重对保费的范围影响不大.

3 )当权重λ1取0.4时，不同的保费和风险规避程度对零售商和供应商期望利润的影响.其中保费分别取:T1=Tmin，T2=5/4Tmin，T3=4/5Tmax及T4=Tmax.

由图5，6可知，使用调整后的保险契约，可以达到供应链渠道的完美协调.

4 结论

文中针对一个风险中性的供应商和一个风险规避的零售商组成的供应链协调问题进行了探讨.以CVaR风险度量准则来刻画零售商的风险，以权衡期望利润和CVaR利润作为具有风险规避特性的零售商的决策目标函数，通过保险契约来协调整个供应链.通过研究得出:

1 )普通的批发价格契约下，零售商的最优订货量小于整个供应链的最优订货量，无法实现供应链的协调.

2 )批发价格契约下，零售商的最优订货量以及零售商、供应商和整个供应链的期望利润都随着风险规避程度η和权重λ的增大而呈现不减趋势.

3 )传统的保险契约已无法实现供应链的协调，通过建议后调整的保险契约可以实现供应链的完美协调.

文中只考虑了零售商的风险态度，零售商和供应商都具有风险规避特性，保险契约还能否实现供应链的协调，信息不对称以及多个决策主体下结论是否适用，这都是未来进一步的研究方向.

References)

［1］ Gan X，Sethi S，Yan H.Coordination of a supply chain with risk-averse agents［J］.Production and OperationsManagement，2004，13(2):135－149.

［2］ Gan X，Sethi S，Yan H.Channel coordination with a risk-neutral supplier and a downside-risk-averse Retailer［J］.Production and Operations Management，2005，14(1):80－89.

［3］ Chhaing H.Supply chain coordination model with retailer’s risk attitudes［R］.Toyonaka:Osaka University，2008.

［4］ Lin Z，Cai C，Xu B.Supply chain coordination with insurance contract［J］.European Jouralof Operational Research，2010，205(2):339－345.

［5］ Chen P.Portfolio setting of insurance contracts when facing a retailer with unknown risk preference［D］.Taiwan:National Central University，2011.

［6］ Yang L，Xu M H，Yu G，et al.Supply chain coordination with CvaR criterion［J］.Asia-Pacific Journal of Operational Research，2009，26(1):135－160.

［7］ Liao Y J，Shi L F.V2G reserve power supply coordination based on CvaR model［J］.Advanced Materials Research，2013，608:1637－1642.

［8］ Xu M，Chen F Y.Tradeoff between expected reward and conditional value-at-risk criterion in newsvendor models［C］//Industrial Engineering and Engineering Management.［s.L.］:IEEE，2007:1553－1557.

［9］ Xu M，Li J.Optimal decisions when balancing expected profit and conditional value-at-risk in newsvendor models［J］.Journal of Systems Science and Complexity，2010，23(6):1054－1070.

［10］ Gao F，Chen F Y，Chao X.Jointoptimal ordering and weather hedging decisions:mean-CVaR model［J］.Flexible Services and Manufacturing Journal，2011，23 (1):1－25.

［11］ Waring A C.Risk-averse selective newsvendor problems［D］.Ann Arbor:University of Michigan，2012.

［12］ 林强，叶飞，陈晓明.随机弹性需求条件下基于CVaR与收益共享契约的供应链决策模型［J］.系统工程理论与实践，2011，31(12):2296－2307.

Lin Qiang，Ye Fei，Chen Xiaoming.Decision models for supply chain based on CVaR and revenue sharing contract under stochastic elastic demand［J］.Systems Engineering-Theory＆Practice，2011，31(12):2296－2307.(in Chinese)