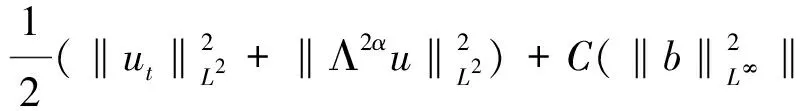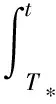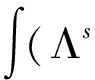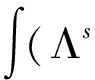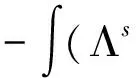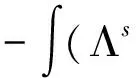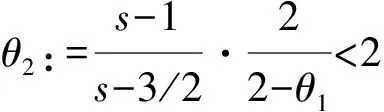A blowup criterion for the 3D generalizedMHD system with zero magnetic diffusivity

Jishan Fan, Gen Nakamura, Yong Zhou

(1.Department of Applied Mathematics, Nanjing Forestry University, Nanjing 210037, China;2.Department of Mathematics, Inha University, Incheon 402-751, Korea;3.School of Mathematics, Shanghai University of Finance and Economics, Shanghai 200433, China;4.Department of Mathematics, Faculty of Science King Abdulaziz University, Jeddah 21589, Saudi Arabia)

1 Introduction

In this paper,we consider the following 3D generalized MHD system:

∂tu+u·u+b,

(1)

∂tb+u·b-b·u+η(-Δ)βb=0,

(2)

divu=divb=0,

(3)

(u,b)(·,0)=(u0,b0)(·) in3.

(4)

Hereuis the fluid velocity field,πis the pressure andbis the magnetic field.μ≥0,α>0,β>0 andη≥0 are physical constants.

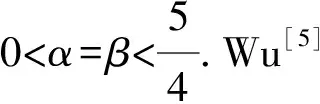
(5)

are satisfied.

The aim of this paper is to prove a new blowup criterion.We will prove

Theorem1Letμ=1,η=0 andu0,b0∈Hs(3) with divu0=divb0=0 andandωsatisfy

(6)

with 00.

Remark1Similar result has been proved in the 2D case by Z.Ye[6].

Remark2Testing (1) byuand using (3),we see that

(b·)b·udx.

(7)

Similarly,testing (2) byband using (3),we find that

(b·)u·bdx.

(8)

Summing up (7) and (8) and noting the cancellation of the last terms on the right hand side of (7) and (8),we have the well-known energy equality

(9)

which implies

u∈L2(0,T;Hα)

and thus

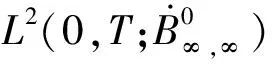
(10)

Our proof will use the following bilinear commutator estimates due to Kato-Ponce[7]:

‖Λs(fg)-fΛsg‖Lp≤C(‖f‖Lp1‖Λs-1g‖Lq1+‖Λsf‖Lp2‖g‖Lq2),

(11)

We will also use the following logarithmic Sobolev inequality [8]

‖

(12)

2 Proof of Theorem 1

This section is devoted to the proof of Theorem 1.We only need to establish a priori estimates.

First,we still have (9).

Due to (6),one concludes that for any small constant>0,there existsT*

For anyT*

(b·)u·bdx≤‖

whence

(13)

Solving (13) in the interval [T*,t],one has

‖b(·,t)‖Lp≤‖b(·,T*)‖Lp(e+y(t))C0

(14)

withCandC0independent ofp.

Takingp→+∞ in (14),we see that

‖b‖L∞≤C(e+y(t))C0.

(15)

Testing (1) by -Δuand using (3),we infer that

(16)

Similarly,testing (2) by -Δband using (3),we deduce that

(17)

Summing up (16) and (17) and noting the cancellation of the last term on the right hand side of (16) and (17),we obtain

which yields

‖

(18)

Testing (1) byut+(-Δ)αuand using (3),(15) and (18),we get

(b·b-u·u)(ut+Λ2αu)dx≤

(‖b‖L∞‖b‖L2+‖u‖L6‖u‖L3)(‖ut‖L2+‖Λ2αu‖L2)≤

C(‖b‖L∞‖b‖L2+‖u‖L6‖u‖H1+α)(‖ut‖L2+‖Λ2αu‖L2)≤

which implies

(19)

Testing (2) bybtand using (3),(15) and (18),we deduce that

C(e+y(t))C0.

(20)

Applying ∂tto (1),testing byutand using (3),(15),(18),(19) and (20),we have

which yields

(21)

Testing (1) by Λ2αuand using (3),(15),(18),(19) and (21),we have

‖Λ2αu‖L2≤C(‖ut‖L2+‖b‖L∞‖b‖L2+‖u‖L6‖u‖L3),

from which and the Gagliardo-Nirenberg inequality

‖u‖L3≤C‖

we have

‖Λ2αu‖L2≤C(e+y(t))C0.

(22)

Applying Λsto (1),testing by Λsuand using (3),we get

(u·u)-u·Λsu)Λsudx+

(23)

Applying Λsto (2),testing by Λsband using (3),we have

(u·b)-u·Λsb)Λsbdx+

(24)

Summing up (23) and (24) and noting the cancellation of the last term on the right hand side of (23) and (24),we have

I1+I2+I3+I4.

(25)

Using (11) and (12),we boundI1as follows.

I1≤C‖

Using (11) and the following Gagliardo-Nirenberg inequalities

‖

we boundI2as follows.

I2≤C‖

Similarly we boundI3+I4as follows.

I3+I4≤C‖b‖L6‖Λsb‖L2‖Λsu‖L3

I5can be bounded by the same method as that ofI2.

Inserting the above estimates into (25) and takingsmall enough and using the Gronwall inequality,we arrive at

‖u‖L∞(0,T;Hs)+‖u‖L2(0,T;Hs+α)≤C,

(26)

‖b‖L∞(0,T;Hs)≤C.

(27)

(28)

which gives

‖Λ2αu‖L∞(0,T;L2)≤C.

Then it is easy to infer that

‖b‖L∞(0,T;W1,6)≤C.

This completes the proof.

:

[1] J. Wu.Generalized MHD equations [J].J Differential Equations,2003,195:284-312.

[2] J. Wu.Regularity criteria for the generalized MHD equations [J].Comm Partial Differential Equations,2008,33:285-306.

[3] J. Fan,H. Gao,G. Nakamura.Regularity criteria for the generalized magnetohydrodynamic equations and the quasi-geostrophic equations[J].Taiwanese J Math,2011,15(3):1059-1073.

[4] Y. Zhou.Regularity criteria for the generalized viscous MHD equations [J].Ann I H Poincare-AN,2007,24:491-505.

[5] J. Wu.Global regularity for a class of generalized magnetohydrodynamic equations [J].J Math Fluid Mech,2011,13:295-305.

[6] Z. Ye.Two regularity criteria to the 2D generalized MHD equations with zero magnetic diffusivity [J].J Math Anal Appl.(in press).

[7] T. Kato,G. Ponce.Comutator estimates and the Euler and Navier-Stokes equations [J].Comm Pure Appl Math,1988,41:891-907.

[8] H. Kozono,T. Ogawa,Y. Taniuchi.The critical Sobolev inequalities in Besov spaces and regularity criterion to some semilinear evolution equations [J].Math Z,2002,242:251-278.