The tensor algebras of Yetter-Drinfeld module

Yanhua Wang

(School of Mathematics, Shanghai University of Finance and Economics)

1 Introduction

LetHbe a Hopf algebra (bialgebra),a left-left Yetter-Drinfeld module over Hopf algebra (bialgebra)His ak-linear spaceVwhich is a leftH-module,a leftH-comodule and satisfies a certain compatibility condition.Yetter-Drinfeld modules were introduced by Yetter in [1] under the name of "crossed bimodule".Radford proved that pointed Hopf algebras can be decomposed into two tensor factors,one factor of the two factors is no longer a Hopf algebra,but a rather a Yetter-Drinfeld Hopf algebra over the other factor[2].Subsequently,Schauenburg proved that the category of Yetter-Drinfeld module overHwas equivalent to the category of left module over Drinfeld double,and also to the category of Hopf module overH[3],and Sommerhauser studied Yetter-Drinfeld Hopf algebra over groups of prime order[4].

Some conclusions of Hopf algebras can be applied to Yetter-Drinfeld Hopf algebras.For example: Doi considered the Hopf module theory of Yetter-Drinfeld Hopf algebras in [5],Scharfschwerdt proved the Nichols Zoeller theorem for Yetter-Drinfeld Hopf algebras in [6],and Andruskiewitsch and Schneider gave the trace formula for Yetter-Drinfeld Hopf algebras in [7].

In this paper,we generalized the antipode properties of Hopf algebras to Yetter-Drinfeld Hopf algebras.We proved the antipode of a Yetter-Drinfeld Hopf algebra is an anti-algebra and anti-coalgebra map,see Proposition 1 and Proposition 2.We study the tensor algebra of Yetter-Drinfeld module,and show that the tensor algebra of Yetter-Drinfeld module is a Yetter-Drinfeld Hopf algebra under a tensor multiplication and a "twisted" comultiplication,see Theorem 4.

In the following,kwill be a field.All algebras and coalgebras are overk.All unadorned ⊗ are taken overk.

2 Preliminaries of Yetter-Drinfeld Hopf algebras

(ab) →v=a→ (b→v), 1 →v=v.

The arrow → denotes left module action.The category of leftA-module is denoted byAM.

Let (C,△,) be a coalgebra.A leftC-comodule is ak-vector spaceVtogether with ak-linear mapρ:VC⊗V:v∑v-1⊗v0such that

∑v-2⊗v-1⊗v0=∑v-1⊗(v0)-1⊗(v0)0, ∑(v-1)v0=v.

The category of leftC-module is denoted byCM.

Let (H,m,u,△,,S) be a Hopf algebra with antipodeS.A left Yetter-Drinfeld module overHis ak-vector spaceVwhich is both a leftH-module and leftH-comodule and satisfies the compatibility condition

∑(h→v)-1⊗(h→v)0=∑h1v-1Sh3⊗h2→v0,

(1)

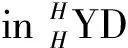
(a1)Ais a leftH-module algebra,i.e.,

h→(ab)=∑(h1→a)(h2→b),h→1A=(h)1A.

(a2)Ais a leftH-comodule algebra,i.e.,

ρ(ab)=∑(ab)-1⊗(ab)0=∑a-1b-1⊗a0b0,

ρ(1A)=1H⊗1A.

(a3)Ais a leftH-module coalgebra,i.e.,

△(h→a)=∑(h1→a1)⊗(h2→a2),(h→a)=H(h)A(a).

(a4)Ais a leftH-comodule coalgebra,i.e.,

∑a-1⊗(a0)1⊗(a0)2=∑a1-1a2-1⊗a10⊗a20,

∑a-1A(a0)=A(a)1H.

△∘m(a⊗b)=(m⊗m)(id⊗τ⊗id)(△⊗△)(a⊗b)=

∑a1(a2-1→b1)⊗a20b2,

Ais called a Yetter-Drinfeld Hopf algebra or Hopf algebras in Yetter-Drinfeld category if it has an antipodeSthat is a convolution inverse to id,i.e.,

One easily see thatSis bothH-linear andH-colinear.In general,Yetter-Drinfeld Hopf algebras are not ordinary Hopf algebras because the bialgebra axiom asserts that they obey (a5).However,it may happen that Yetter-Drinfeld Hopf algebras are ordinary Hopf algebras when the pre-braiding is trivial,for details see [4].

Next,we give a basic property of Yetter-Drinfeld Hopf algebra.It is well know that the antipode of a Hopf algebra is an anti-algebra and anti-coalgebra map,see [8-10].This is also true for Yetter-Drinfeld Hopf algebra.The following lemma give the character.

S1)S(ab)=∑(a-1→S(b))S(a0),andS(1)=1.

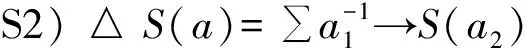
ProofIfSis an anti-algebra automorphism,then we haveSm=m(s⊗s)τands(1)=1.We take the idea of Sweedler in [10,P.74].

We have

(Sm*m)(a⊗b)=

m(Sm⊗m)△(a⊗b)=

m(Sm⊗m)(∑a1⊗a2-1→b1⊗a20⊗b2)=

S(∑a1(a2-1→b1))⊗a20b2=

∑S((ab)1)(ab)2=

u(a⊗b).

On the other hand

(m*m(S⊗S)τ)(a⊗b)=

m(m⊗m(S⊗S)τ)△(a⊗b)=

m(m⊗m(S⊗S)τ)(∑a1⊗a2-1→b1⊗a20⊗b2)=

m∑[a1(a2-1→b1)⊗m(S⊗S)τ(a20⊗b2)]=

m∑[a1(a2-2→b1)⊗m(S⊗S)(a2-1→b2⊗a20)]=

m∑[a1(a2-2→b1)⊗(a2-1→S(b2))S(a20)]=

∑a1(a2-2→b1)(a2-1→S(b2))S(a20)]=

∑a1[a2-1→(b1S(b2))]S(a20)=

∑a1(a2-1→(b))S(a20)=

∑a1(a2-1)(b)S(a20)=

∑u(b)a1S(a2)=u(b)u(a)=u(a⊗b) .

ThusSm*m=m*(m(s⊗s)τ)=u,henceSm=m(s⊗s)τ.By(1)=1 and △(1)=1⊗1,we have (S*id)(1)=S(1)1=u(1)=1.SoS(1)=1.

The proof ofSis an anti-coalgebra automorphism is similar to the proof ofSis an anti-algebra automorphism.

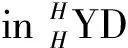
ProofBy assumption,it suffice to prove that if (id*S)(a)=u(a) and (S*id)(b)=u(b),then (id*S)(ab)=u(ab),a,b∈X.

By △(ab)=∑a1(a2-1→b1)⊗a20b2, we have

(id*S)(ab)=∑a1(a2-1→b1)S(a20b2)=

∑a1S(a2)

u(a)u(b)=

u(ab) .

This complete the proof.

3 The tensor algebra of Yetter-Drinfeld module

Assume thatVis a vector space,thenTV=V⨁V⊗V⨁… ⨁V⊗n=T0V⨁T1V⨁T2V⨁…TnVbecomes an algebra with the connected multiplication

(v1⊗v2⊗…⊗vs)(w1⊗w2⊗…⊗wt)=v1⊗v2⊗…⊗vs⊗w1⊗w2⊗…⊗wt.

(2)

We have the following lemma about the tensor algebra of a Yetter-Drinfeld module.

Lemma3LetVbe a left Yetter-Drinfeld module,thenTVis also a left Yetter-Drinfeld module.

ProofDefine the module action and comodule action as follows

h→(v1⊗v2⊗…⊗vn)=∑(h1→v1)⊗(h2→v2)⊗…⊗(hn→vn)

(3)

and

ρ(v1⊗v2⊗…⊗vn)=∑(v1-1v2-1…vn-1)⊗v10⊗v20⊗…⊗vn0,

(4)

∀h∈H,v1⊗v2⊗…⊗vn∈TV.

It is easy to proveTVis a leftH-module.For anyh,g∈H,v1⊗v2⊗…⊗vn∈TV.We have 1→(v1⊗v2⊗…⊗vn)=v1⊗v2⊗…⊗vnand

h→(g→(v1⊗v2⊗…⊗vn))=

∑(h1→g1→v1)⊗(h2→g2→v2)⊗…⊗(hn→gn→vn)=

∑(h1g1→v1)⊗(h2g2→v2)⊗…⊗(hngn→vn)=

(hg)→(v1⊗v2⊗…⊗vn).

TVis a leftH-comodule.Since

(⊗id)ρ(v1⊗v2⊗…⊗vn)=

v1⊗v2⊗…⊗vn

and

(△⊗id)ρ(v1⊗v2⊗…⊗vn)=

(△⊗id)(∑v1-1v2-1…vn-1⊗v10⊗v20⊗…⊗vn0)=

∑(v1-2v2-2…vn-2)⊗(v1-1v2-1…vn-1)⊗(v10⊗v20⊗…⊗vn0)=

(id⊗ρ)ρ(v1⊗v2⊗…⊗vn)

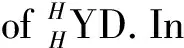
∑(h→(v1⊗v2⊗…⊗vn))-1⊗(h→(v1⊗v2⊗…⊗vn))0=

∑(h1→v1⊗h2→v2⊗…⊗hn→vn)-1⊗(h1→v1⊗h2→v2⊗…⊗hn→vn)0=

∑(h1→v1)-1⊗(h2→v2)-1⊗…⊗(hn→vn)-1⊗(h1→v1)0⊗(h2→v2)0⊗…⊗(hn→vn)0=

∑(h1v1-1S(h3)h4v2-1S(h6)…S(h3n+1)vn-1S(h3n+3)⊗h2→v10⊗h5→v20⊗…⊗h3n+2→vn0=

∑(h1v1-1v2-1…vn-1S(hn+2))⊗h2→v10⊗h3→v20⊗…⊗hn+1→vn0=

∑(h1v1-1v2-1…vn-1S(h3))⊗h2→(v10⊗v20⊗…⊗vn0)=

∑(h1(v1⊗v2⊗…⊗vn)-1S(h3))⊗h2→(v1⊗v2⊗…⊗vn)0.

This complete the proof.

Theorem4IfVis a Yetter-Drinfeld module over Hopf algebraH,then the tensor algebraTVofVis a Yetter-Drinfeld Hopf algebra overH.

ProofFor anyx=v1⊗v2⊗…⊗vs∈TsV,y=w1⊗w2⊗… ⊗wt∈TtV,define the multiplication ofxyas the tensor multiplication

xy=v1⊗v2⊗…⊗vs⊗w1⊗w2⊗…⊗wt.

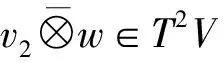
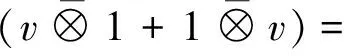
which show that △ is coassociative.

By the comultiplication ofV,forv⊗w∈T2V,we have

△(v⊗w)=(m⊗m)(id⊗τ⊗id)(△(v)⊗△(w))=

(m⊗m)(id⊗τ⊗id)((1⊗v+v⊗1)⊗(1⊗w+w⊗1)=

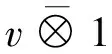
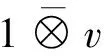
Forv⊗w⊗t∈T3V,the comultiplication ofT3Vis

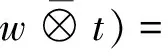
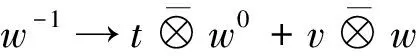
In general,we denote

⊗v2⊗…⊗vn) =

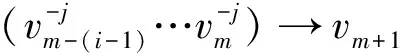
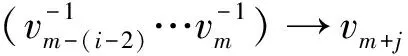
Using the above notation,the comultiplication ofTVis

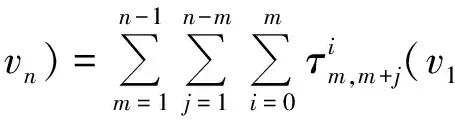
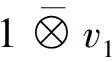
DefineS(v)=-v,v∈V,and

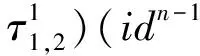
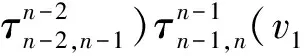
For anyv∈V,we havem(S⊗id)△(v)=s(1)v+vS(1)=0=(v) andm(id⊗S)△(v)=s(v)+vS(1)=0=(v).Therefore,the property of antipode is satisfied for generators ofTV.By Lemma 2,Sis the antipode ofTV.This completes the proof.

:

[1] D.N.Yetter.Quantum groups and representation of monoidal categories [J].Math.Proc.Cambridge Philos.Soc.,1990,108:261-290.

[2] D.Radford.The structure of Hopf algebras with a projection [J].J.Algebra,1985,92:322-347.

[3] P.Schauenburg.Hopf modules and Yetter-Drinfeld modules [J].J.Algebra,1994,169:874-890.

[4] Y.Sommerhauser.Yetter-Drinfeld Hopf algebras over groups of prime order [C]//Lecture Notes in Mathemtics,Vol.1789,Springer,2002.

[5] Y.Doi.Hopf module in Yetter-Drinfeld categories [J].Comm.Algebra,1998,26(9):3057-3070.

[6] Scharfschwerdt.The Nichols-Zoeller theorem for Hopf algebras in the category of Yetter-Drinfeld modules [J].Comm.Algebra,2001,29(6):2481-2487.

[7] Y.Doi.The trace formula for braided Hopf algebras [J].Comm.Algebra,2000,28(4):1881-1895.

[8] S.Dascalescu,C.Nastasescu,S.Raianu.Hopf algebra; An introduction [M].New York:Marcel Dekker,Inc.,2001.

[9] S.Montgomery.Hopf algebras and their actions on rings [C].CBMS Regional Conf.Series in Math.82,Amer.Math.Soc.,Providence,RI 1993.

[10] M.E.Sweedler.Hopf algebras [M].New York:Benjamin,1969.