Stage-structured models for interactingwild and sterile mosquitoes
Jia Li
(Department of Mathematical Sciences, University of Alabama in Huntsville,Huntsville, AL 35899, U.S.A)
1 Introduction
Malaria and other mosquito-borne diseases are a considerable public health concern worldwide.These diseases are transmitted between humans by blood-feeding mosquitoes.No vaccines are available and an effective way to prevent these mosquito-borne diseases is to control mosquitoes.Among the mosquitoes control measures,the sterile insect technique (SIT) has been applied to reducing or eradicating the wild mosquitoes.SIT is a method of biological control in which the natural reproductive process of mosquitoes is disrupted.Utilizing radical or other chemical or physical methods,male mosquitoes are genetically modified to be sterile which are incapable of producing offspring despite being sexually active.These sterile mosquitoes are then released into the environment to mate with wild mosquitoes that are present in the environment.A wild female that mates with a sterile male will either not reproduce,or produce eggs but the eggs will not hatch.Repeated releases of sterile mosquitoes or releasing a significantly large number of sterile mosquitoes may eventually wipe out or control a wild mosquito population[1-3].
While SIT brings an effective weapons to fight vector-borne diseases,and has shown promising in laboratory research,the assessment of the impact of releasing sterile mosquitoes on the wild mosquitoes controlling remains a challenging task.
Mathematical models have proven useful in getting insights to such challenging questions in population dynamics and epidemiology.There are mathematical models in the literature formulated to study the interactive dynamics of mosquito populations or the control of mosquitoes[4-10].In particular,models incorporate different strategies in releasing sterile mosquitoes have been formulated and the studied in [11,12].However,the mosquito population has been assumed to be homogeneous without distinguishing the metamorphic stages of mosquitoes.
Mosquitoes undergo complete metamorphosis going through four distinct stages of development during a lifetime: egg,pupa,larva,and adult[13].While interspecific competition and predation are rather rare events and could be discounted as major causes of larval mortality,intraspecific competition could represent a major density dependent source for the population dynamics,and hence the effect of crowding could be an important factor in the population dynamics of mosquitoes[14-16].Hence,to have a better understanding of the impact of the releases of sterile mosquitoes,the metamorphosis stage structure needs to be included[17].Nevertheless,to keep our mathematical modeling as simple as possible,due to the fact that the first three stages in a mosquito′s life cycle are aquatic,we follow a line similar to the stage-structured models for transgenic mosquitoes in [18-20] where the three aquatic metamorphic stages are combined as one group,we group the three aquatic stages of mosquitoes into one class,called larvae,and divide the mosquito population into only two classes.We still simplify our models such that no male and female individuals are distinguished,and assume that the mosquito populations follow the nonlinearity of Ricker-type[21].We first give general modeling descriptions in Section 2.We then formulate a model,similar to that in [4,5,11,12],where the number of releases of sterile mosquitoes is constant in Section 3.Complete mathematical analysis for the model dynamics is given.We then formulate a model for the case where the number of sterile mosquito releases is proportional to the wild mosquito population size in Section 4.Mathematical analysis and numerical examples are provided to demonstrate the complexity of the model dynamics.To provide a different releasing strategy,we assume,in Section 5,that releases are of Holling-II type such that the number of sterile mosquitoes is proportional to the wild mosquito population size when the wild mosquito population size is small but is saturated and approaches a constant as the wild mosquito population size is sufficiently large.We also provide complete mathematical analysis for the model dynamics.We finally provide brief discussions on our findings,particularly the impact of the three different strategies on the mosquito control measures in Section 6.
2 The model basis
We letxnandynbe the numbers of the larvae and adults of wild mosquitoes at generationn,respectively.In the absence of the interaction between the wild and sterile mosquitoes,we assume that the dynamics of the wild mosquito population are described by the following system:
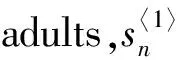
Since the intraspecific competition mainly takes place within the aquatic stages of mosquitoes,we assume that the density-dependent larvae mortality rate and the emergence rate to adults are both functions of the larvae size only.We further assume the Ricker-type nonlinearity for the survival functions.Then the dynamics are governed by the following system:
xn+1=ayne-d-k1xn,
yn+1=βxne-d-k2xn,
wheredi>0,i=1,2 are the density-independent death rates,ki>0,i=1,2,are the constants describing the carrying capacities of different larvae stages.For convenience,by further merginge-diintoaandβ,respectively,and keeping the same notationsaandβ,we have the basic system for the stage-structured model
xn+1=ayne-k1 xn,
yn+1=βxne-k2xn.
(1)
The origin (0,0) is a trivial fixed point of system (1).Define the intrinsic grow rate of the stage-structured mosquito populationr0:=aβ.The trivial fixed point is locally asymptotically stable ifr0<1 and is unstable ifr0>1.

(2)
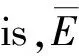
(3)
and is unstable if
(4)
We summarize these basic results as follows.
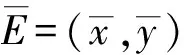
Now suppose sterile mosquitoes are released into the field of wild mosquitoes and we letBnbe the number of sterile mosquitoes released at generationn.Since sterile mosquitoes do not reproduce,their population size at generationn+1 has no input from their size atn.HenceBnonly depends on the size of the releases of the sterile mosquitoes.After the sterile mosquitoes are released,the mating interaction between the wild and sterile mosquitoes takes place.Following the line of the homogeneous population models in [22,23],we assume harmonic means for matings such that the per capita birth rate is given by
whereC(Nn) is the number of matings per mosquitoes withNn=yn+Bn,the total adult mosquito population size,andais the number of wild larvae produced per wild mosquito.The interactive dynamics of wild and sterile mosquitoes are then described by the following system:
yn+1=βxne-k2xn.
(5)
3 Constant releases
We first consider the case whereBn:=bis a constant which means sterile mosquitoes are constantly released for each generation,and assume that the number of matingsC(Nn) is a constant and is merged into the birth rateawith the same notation for convenience.Then system (5) becomes
yn+1=βxne-k2xn.
(6)
Clearly,the origin (0,0) is a fixed point and is always locally asymptotically stable.Let (x,y) be a positive fixed point.Then it satisfies the following equations
y=βxe-k2x,
which leads to
and then
b=aβxe-(k1+2k2) x-βxe-k2x=βxe-(k1+2k2)x(r0-e(k1+k2)x) :=βH(x),
FunctionH(x)>0,forx>0,only ifr0>1.Hence ifr0≤1,there exists no positive fixed point.
We assumer0>1,and only considerx∈Ωwhere setΩis defined by
(7)
We further assume condition in (3) is satisfied such that the wild mosquitoes maintain a locally steady state before sterile mosquitoes are released.
From
H′(x)=e-(k1+2k2) x(r0(1-(k1+2k2)x)-e(k1+k2)x(1-k2x)),
we define lineL(x):=r0(1-(k1+2k2)x) and functionF(x) :=e(k1+k2)x(1-k2x).ThenH′(x)=0 forx≥0 if and only ifL(x)=F(x) forx≥0.
Since
(8)
and
F″(x)=(k1+k2)(k1-k2-(k1+k2)k2x),
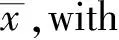
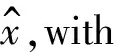
Then ifx>1/k2,
which implies
(k1+k2)x>lnr0,
and hencex∉Ω.
We next investigate the stability of the positive fixed points.The Jacobian at a positive fixed point has the form of
Since

a positive fixed point (x,y) is locally asymptotically stable if
or
(9)
Supposek1 k1x<1 (10) Then a positive fixed point is locally asymptotically stable if the right inequality in (9) holds,that is (k2x-1)b<(2-k2x)(b+y), or (11) provided 1 On the other hand,ifk2x<1,the right equality in (9) is satisfied.Then a positive fixed point is locally asymptotically stable if the left inequality in (9) holds,that is or (12) Substitutingy=βxe-k2xinto (11) and (12),respectively,we have the results as follows. H(x) :=xe-(k1+2k2)x(r0-e(k1+k2)x). (13) or (14) We give the following example to demonstrate the results in Theorem 2. Example1Choose the following parameters a=2.25,β=0.8,k1=0.2,k2=0.3. (15) To have a more optimal and economically effective strategy for releasing sterile mosquitoes in an area where the population size of wild mosquitoes is relatively small,instead of releasing sterile mosquitoes constantly,we may consider to keep closely sampling or surveillance of the wild mosquitoes and let the releases be proportional to the population size of the wild mosquitoes such that the number of releases isB(·)=bywherebis a constant. We assume that there is no mating difficulty even as the mosquito population size is low.Then the model dynamics are described by the following system: yn+1=βxne-k2xn. (16) The system becomes,mathematically,the same system as (1).Define the sterile mosquito release threshold asbc:=aβ-1.The trivial fixed point (0,0) locally asymptotically stable ifb>bcand is unstable ifb (17) ifb Define the stability threshold for the positive fixed point as (18) If there exists a unique fixed pointE*,then it is locally asymptotically stable ifb>bs,and is unstable ifb Theorem3The trivial fixed point (0,0) for system (16) is locally asymptotically stable ifb>bcand is unstable ifb Notice that the stability condition is resulted fromr0/(1+b) Example2We use,in this example,the following parameters a=40,β=0.8,k1=0.2,k2=0.3, (19) and the dynamical features are presented in Figure 2.Sincer0=32>e2(k1+k2)/k2=28.03,the positive fixed point in the absence of releases of sterile mosquitoes is unstable.After the releases of sterile mosquitoes,the threshold value of releases isbc=aβ-1=31 and the the stability threshold isbs=0.1416.Whenb=0.13 Figure 2 The parameters are given in (19).The two threshold values arebc=31 andbs=0.1416.Whenb=0.13,there exists a unique positive fixed point,which is unstable as shown in the upper left figure.Forbs (20) We define an initial sterile mosquitoes release thresholdb0:=aβ-1=r0-1 such that the origin (0,0) is locally asymptotically stable ifb>b0and is unstable ifb A positive fixed point (x,y) satisfies b+1+y=aβ(1+y) e-(k1+k2)x, that is, b=(1+βxe-k2x)(r0e-(k1+k2)x-1). (21) Then we only considerx∈Ω,withΩgiven in (7). Define Then and and that ifb Forb>b0,notice thatf2is independent ofband that asbincreases,the graph of the curve off1(x) moves up.Then there exists a threshold value of releasesbc>b0such that ifb>bc,b=bc,orb0 (1+βxe-k2x)r0(k1+k2) e-k1 x=β(1-k2x)(r0e-(k1+k2)x-1), that is (22) Notice that the left right hand side of (22) is an increasing function ofx,forx<1/k2,and the right hand side of (22) is a decreasing function ofx,respectively.Hence there exists a unique solutionxc∈[0,1/k2] for (22).Substitutingxcinto (21) then gives the threshold value of releasesbc. We then investigate the stability of the positive fixed points.The Jacobian at a positive fixed pointE=(x,y) has the form of ThenEis locally asymptotically stable if that is, or (k1-k2)x(1+y)2<((k2-k1)x(1+y)-(1-k2x)y)b. (23) Thus,it is easy to see thatEis unstable ifk2 Supposek1 b(k1-k2+(1-(2k2-k1)x)βe-k2x)<(k2-k1)(1+βxe-k2x), (24) or (25) if the denominate is positive,wherexis the component of the positive fixed pointE.ThenEis locally asymptotically ifbs>b,and is unstable ifbs We summarize our results as follows. Theorem4Supposek1 bc=(1+βxce-k2 xc)(r0e-(k1+k2) xc-1), wherexcis the unique solution of equation (22).Then there exist no,one,or two positive fixed points to system (20),ifb>bc,b=bc,orb0 We give an example to demonstrate the existence and stability results for model system (20) as follows. Example3Choosing the following parameters a=2.25,β=0.8,k1=0.02,k2=0.03, We introduced the metamorphic stage structure of mosquitoes into dynamical models for the interactive wild and sterile mosquitoes to study the impact of the releases of sterile mosquitoes in this paper.We simplify the models by combing the three aquatic metamorphic stages into one group,called larvae,and assume that the density-dependence,due to intraspecific competition,is only on the larvae.We considered three different strategies for the releases in model systems (6),(16),and (20),respectively.We determined the threshold value of the releases,bc,and the stability threshold value for positive fixed points,bs,for each of the model systems.Ifb>bc,there exists no positive fixed point for all of the three model systems,in which case the wild mosquito population will be wiped out if the origin is stable,or oscillates.Ifb While the biological outcomes from the model systems in this paper are similar to those in [12],particularly as the density-dependence is assumed to be only based on the larvae,as the stage structure is included in the three model systems,the mathematical analysis becomes more challenging.We have managed to obtain fundamental results from our model systems,but some of the mathematical analysis is not complete.Further research is planned in the near future. : [1] L.Alphey,M.Benedict,R.Bellini,G.G.Clark,D.A.Dame,M.W.Service,S.L.Dobson.Sterile-insect methods for control of mosquito-borne diseases: An analysis[J].Vector-Borne and Zoonotic Diseases,2010,10:295-311. [2] A.C.Bartlett,R.T.Staten.Sterile Insect Release Method and other Genetic Control Strategies [M/OL] Radcliffe′s IPM World Textbook,1996,http://ipmworld.umn.edu/chapters/bartlett.htm. [3] Wikipedia.Sterile insect technique[J/OL] 2014,http://en.wikipedia.org/wiki/Sterile_insect_technique. [4] H.J.Barclay.The sterile insect release method for species with two-stage life cycles [M].Researches on Population Ecology,1980,21:165-180. [5] H.J.Barclay.Pest population stability under sterile releases [J].Res.Popul.Ecol.,1982,24:405-416. [6] H.J.Barclay.Modeling incomplete sterility in a sterile release program:interactions with other factors [J].Popul Ecol,2001,43:197-206. [7] H.J.Barclay.Mathematical models for the use of sterile insects [C]//Sterile Insect Technique.Principles and Practice in Area-Wide Integrated Pest Management,(V.A.Dyck,J.Hendrichs,and A.S.Robinson,Eds.),Heidelberg,Springer,2005:147-174. [8] H.J.Barclay,M.Mackuer.The sterile insect release method for pest control:a density dependent model [J].Environ.Entomol.,1980,9:810-817. [9] K.R.Fister,M.L.McCarthy,S.F.Oppenheimer,Craig Collins.Optimal control of insects through sterile insect release and habitat modification [J].Math.Biosci.,2013,244:201-212. [10] J.C.Floresa.A mathematical model for wild and sterile species in competition: immigration [J].Physica A,2003,328:214-224. [11] Liming Cai,Shangbing Ai,Jia Li.Dynamics of mosquitoes populations with different strategies of releasing sterile mosquitoes,(preprint). [12] Jia Li,Zhiling Yuan.Modeling of releasing sterile mosquitoes with different strategies,(preprint). [13] N.Becker.Mosquitoes and Their Control [M].New York:Kluwer Academic/Plenum,2003. [14] C.Dye.Intraspecific competition amongst larval aedes aegypti: Food exploitation or chemical interference [J].Ecological Entomology,1982,7:39-46. [15] R.M.Gleiser,J.Urrutia,D.E.Gorla.Effects of crowding on populations of aedes albifasciatus larvae under laboratory conditions [J].Entomologia Experimentalis et Applicata,2000,95:135-140. [16] M.Otero,H.G.Solari,N.Schweigmann.A stochastic population dynamics model for Aedes aegypti: formulation and application to a city with temperate climate [J].Bull.Math.Biol.,2006,68:1945-1974. [17] Junliang Lu,Jia Li.Dynamics of stage-structured discrete mosquito population models [J].J.Appl.Anal.Compt.,2011,1:53-67. [18] Jia Li.Simple stage-structured models for wild and transgenic mosquito populations [J].J.Diff.Eqns.Appl.,2009,17:327-347. [19] Jia Li.Malaria model with stage-structured mosquitoes [J].Math.Biol.Eng.,2011,8:753-768. [20] Jia Li.Discrete-time models with mosquitoes carrying genetically-modified bacteria [J].Math.Biosci.,2012,240:35-44. [21] W.E.Ricker.Stock and recruitment [J].Journal of the Fisheries Research Board of Canada,1954,11:559-623. [22] Jia Li.Simple mathematical models for interacting wild and transgenic mosquito populations [J].Math.Biosci.,2004,189:39-59. [23] Jia Li. Modeling of mosquitoes with dominant or recessive transgenes and Allee effects [J].Math.Biosci.Eng.,2010,7:101-123.

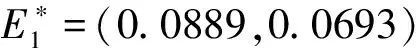

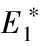
4 Releases proportional to the wild mosquito population size

5 Proportional releases with saturation
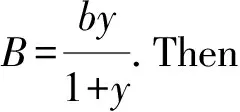
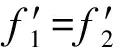
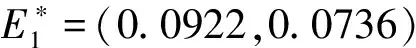

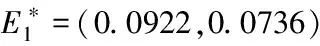
6 Concluding remarks

