基于EGARCH模型的黄金周对中国股市影响研究

白胜高，李沛嬴

（1.上海金融学院，上海201209；2.天津工业大学，天津200287）

一、引 言

国内外学者对股票市场进行过大量实证研究，早已发现“周末效应”、“节日效应”等现象的存在。如国外，Wilson（1993）发现，纽约证券交易所、美国证券交易所和全国证券交易商自动报价系统协会的数据均存在节前效应；Ryan Chong（2005）发现，1991至2003年美国股市股票市场、英国股票市场和香港股票市场都存在节前效应。而国内，严太华（2000）和田华（2003）发现，中国股市有正的周五效应和负的周一效应。义垂林（2005）发现春节、劳动节、国庆节均有节前效应和节后效应。陆磊（2008）发现，春节、劳动节有正的节前效应。遗憾的是，当人们对于股票市场上的这一价格异常波动已基本达成共识时，却难以找到文献对这一现象给出的合理解释。

本文认为，股票价格的波动受到投资者的投资行为影响，除了股票的基本面信息外，投资者的投资行为很大程度上取决于政府政策、事件、市场信息透明程度以及投资者对以上信息的信心程度与预期好坏。换句话说，在投资者对股票的基本面信息了解相当的前提下，如果投资者对未来政府出台的政策或可能发生的重大事件持乐观的态度，那么股票市场的投资行为将会推动股票价格的上升，反之股票价格将可能下跌。我国股票市场由于起步较晚，很多方面尚不够成熟，投资者的投资行为多为“投机行为”，股票的价格波动往往受到事件影响，尤其是国家政策影响。根据王垒（2003）的研究，认为国家政策对决策影响比较重要和非常重要的证券投资者占到了87.8%，而认为不重要的仅占3.9%，这说明我国股票市场的投资者存在非常严重的“政策依赖”心理。

但是，股票市场“周末效应”和“节日效应”等价格波动异常现象的真正原因很可能是市场休市。因为这类现象具有一个共同点，那就是发生在休市期前后。投资者对未来的预期会反映到投资行为上，休市期间极有可能发生对未来股票市场产生影响的事件，并且投资者对这些事件的心理预期异于其他时间，休市越长，心理预期的情况可能越不相同。不同的心理预期反映到投资行为上，从而便出现了在周末前后或节假日前后股票价格的波动异常。

为验证我们的分析，本文选取我国特有的黄金周长假为例进行实证研究。因为我国黄金周长假政策，国内股票市场休市期较长，投资者对这段时间内将会发生事件的心理预期应该更加明显不同于平时，所以如果推断正确，那么黄金周前后一个交易日的股票价格相较于其他交易日应该会存在显著的波动异常。

二、实证研究

（一）数据选择与处理

中国特色的黄金周起始于1999年，国务院对春节、劳动节和国庆节的休假时间进行了统一调整，将节日前后的两个周末四天和法定假期三天集中为共计七天的长假，形成真正意义上的“黄金周”，但这一政策的正式实施是从2000年国庆节开始。

所以，本文以上证指数为例，从大智慧软件上下载2000年6月1日到2013年10月31日的上证指数收盘价格的日数据作为原始时间序列｛Yt｝。为减少异方差，对序列进行自然对数处理LNYt＝lnYt，这样一共得到3247个数据。接下来，我们将对这一时间序列｛LNYt｝进行深入研究。

序列｛LNYt｝的描述性统计如图1和表1所示。

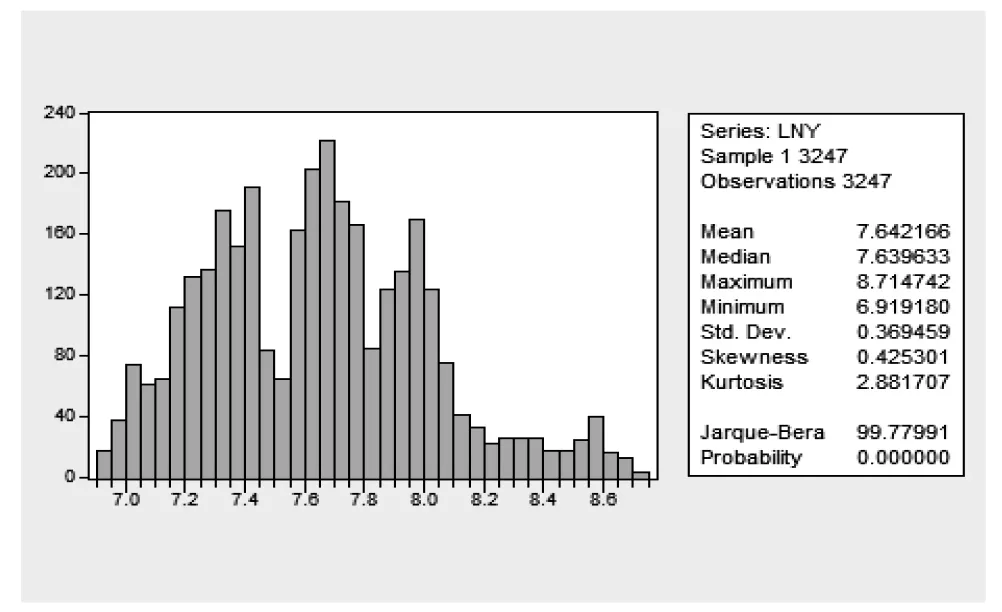
图1 序列描述性统计图

表1 序列描述性统计表

由图1和表1可以看出，序列｛LNYt｝的偏度大于0，峰度小于3，JB统计量较大，说明分布具有右偏性，分布较正态分布平坦，不服从正态分布。

（二）数据检验与模型建立

为对所研究时间序列建立一个拟合度高的模型，首先考虑该序列的平稳性。我们使用ADF检验法对数据进行检验。从表2可以看出，t统计量的值大于显著性水平为10%的临界值，故不能拒绝LNY有单位根的原假设，说明是一个非平稳序列。

表2 LNY序列的单位根检验结果

所以我们对序列进行一阶差分，再对差分后的序列进行平稳性检验，结果如表3所示。

表3 D（LNY）序列的单位根检验结果

可以看出t统计量明显小于显著性水平为1%的临界值，故拒绝存在单位根的原假设，也就是说一阶差分后的序列为平稳序列。这符合英国统计学家肯德尔提出的“股价遵循随机游走规律”的结论。形式为：

模型的估计结果如表4所示。

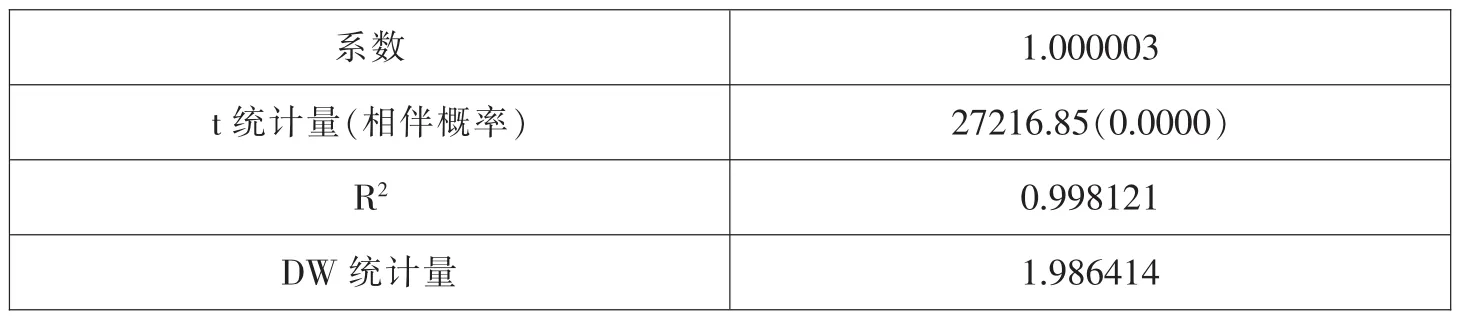
表4 随机游走模型的估计结果

从各项统计指标可以看出，模型拟合程度较好，但是我们进一步观察残差图（如图2）发现了波动的“成群”效应，即数据在一段时间内波动很强，在另一段时间内波动又很弱。这表明残差项可能具有条件异方差性。

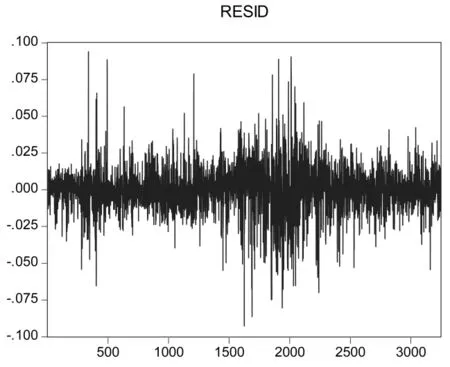
图2 残差序列图

于是，对残差序列进行拉格朗日乘数（LM）检验，当滞后阶数q＝4时，得到如表5结果。

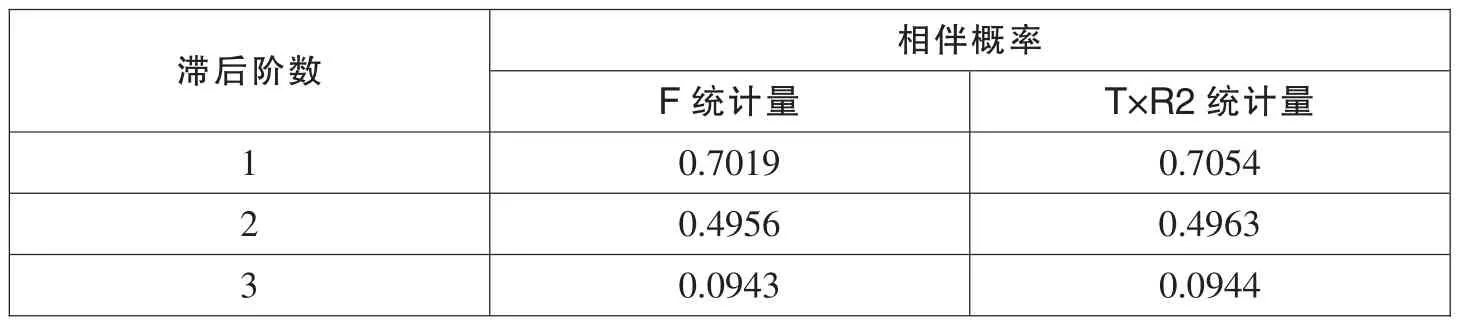
表5 残差序列的拉格朗日检验结果

可以看出，F统计量的相伴概率等于0.0263，T×R2统计量的相伴概率为0.0264，明显小于0.05。这表明模型存在高阶ARCH效应，即条件异方差性，所以我们考虑建立 GARCH（p，q）模型。

我们对序列建立GARCH（1，1）模型，重新估计后得到的结果如表6。

表6 GARCH（1，1）模型的方差方程参数

再对重新估计后的模型进行ARCH－LM检验，以考察残差项的异方差性，选取滞后阶数为1，如表7所示，发现F统计量和T×R2统计量的相伴概率均明显大于0.05，表明异方差性已经被消除。

表7 ARCH－LM检验结果

我们再看该模型的拟合情况，方差方程中的ARCH项和GARCH项的系数（α和β）都非负，且系数之和等于0.98716并小于1，满足参数约束条件。但是对残差项进行白噪声检验后发现，该残差序列不是一个白噪声序列，这意味着残差序列还存在没有被提取的信息。

（三）模型调整

为了充分提取残差序列存在的信息，使得模型的残差项为一个白噪声序列，我们考虑调整模型，重新设序列的估计方程为：

经过多次尝试，直到当i＝8时，模型的残差项才通过为一个白噪声序列的检验。我们得到重新估计后的模型结果（如图7），及模型的残差序列自相关图（如表8和表9）。

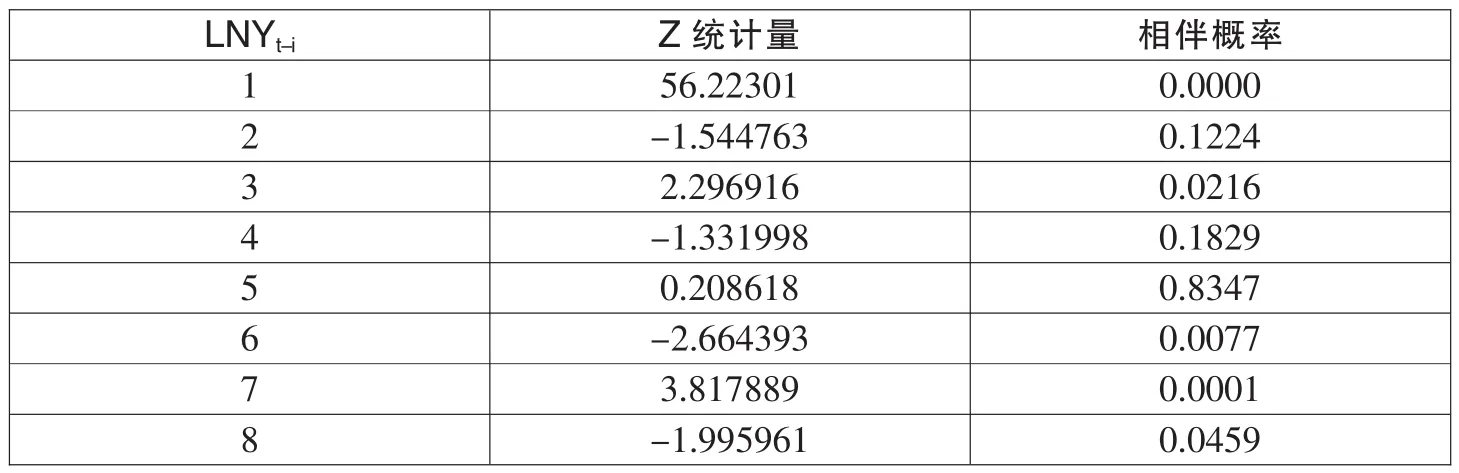
表8 重新估计后的模型结果

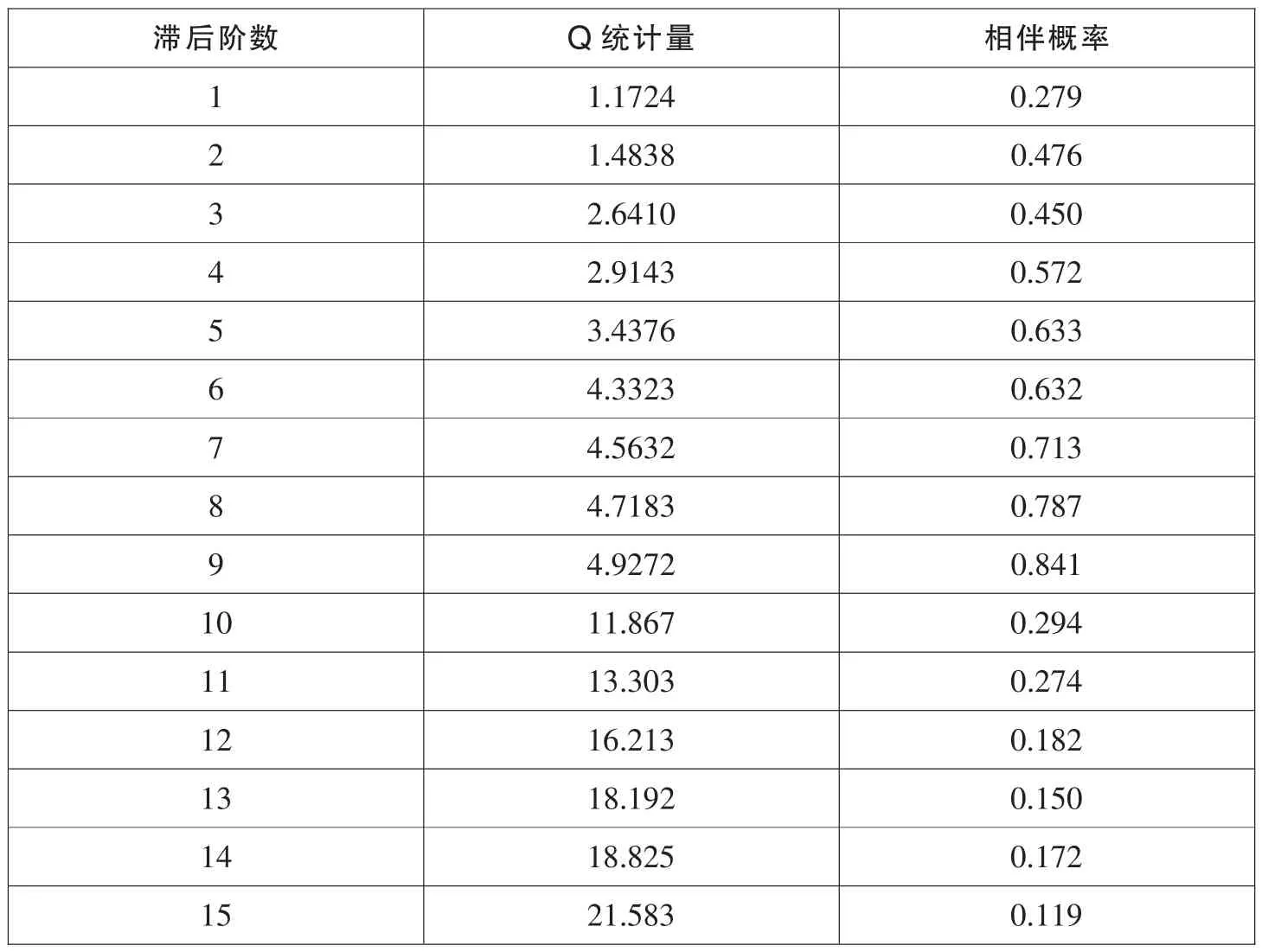
表9 残差序列自相关结果

对该模型残差序列进行Q统计量检验，滞后15阶的所有Q值的相伴概率均明显大于0.05，说明所有Q值都小于检验水平为0.05的χ2分布临界值。也就是说，模型的残差项是一个白噪声序列。

但是，估计模型中的 LNYt－2、LNYt－4、LNYt－5项都不能通过 Z 统计量检验。 剔除这几项之后发现仍然不能使所有LNYt－1项都通过Z统计量检验（如表10）。

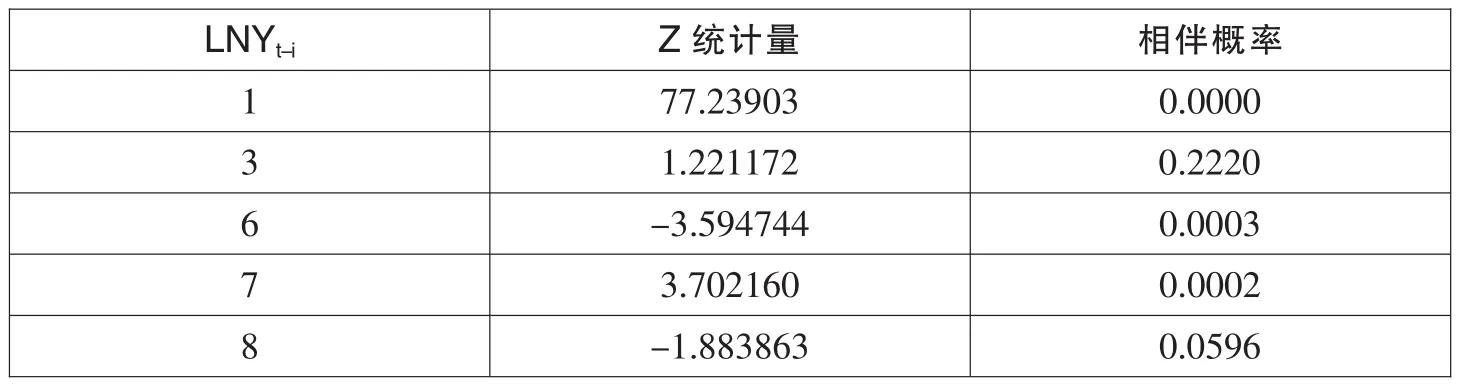
表10 调整模型后各项的Z统计量及相伴概率

于是，基于其他学者对中国股市的波动性研究，猜想中国股票市场可能存在“杠杆效应”，即股票价格面对好消息和坏消息的冲击表现出一种非对称效应。 所以考虑建立 EGARCH（1，1）模型、TARCH（1，1）模型和 PARCH（1，1）模型。

我们首先对式（2）（其中 i＝8）建立 EGARCH（1，1）模型，模型中的条件方差方程如下：

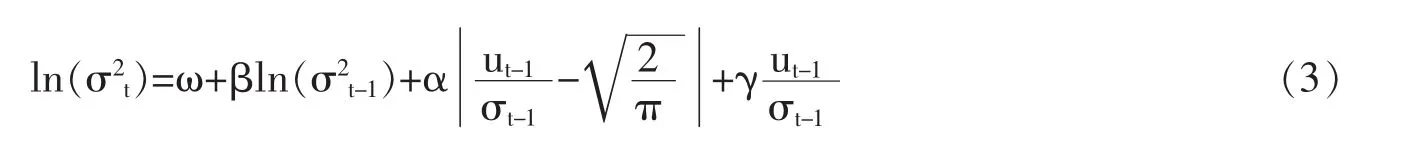
估计结果如表11所示。

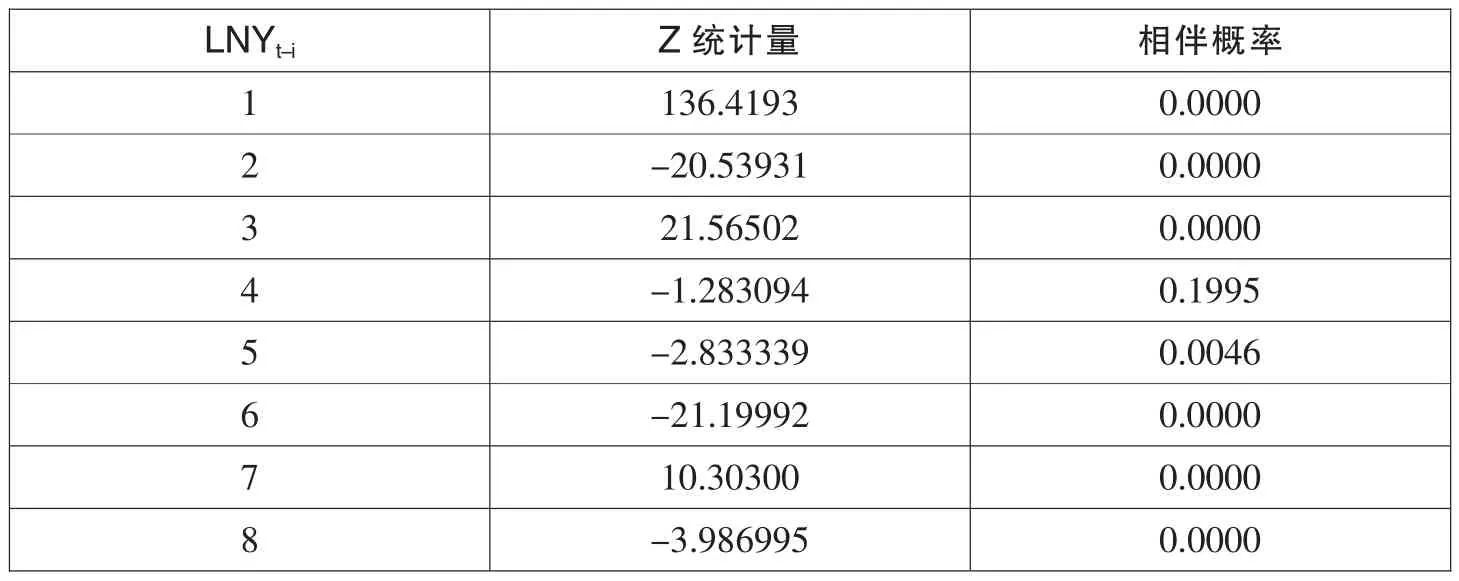
表11 建立EGARCH（1，1）模型后各项的Z统计量及相伴概率

方程中的LNYt－4项不能通过Z统计量检验，对其剔除处理。再次估计模型结果如表12。

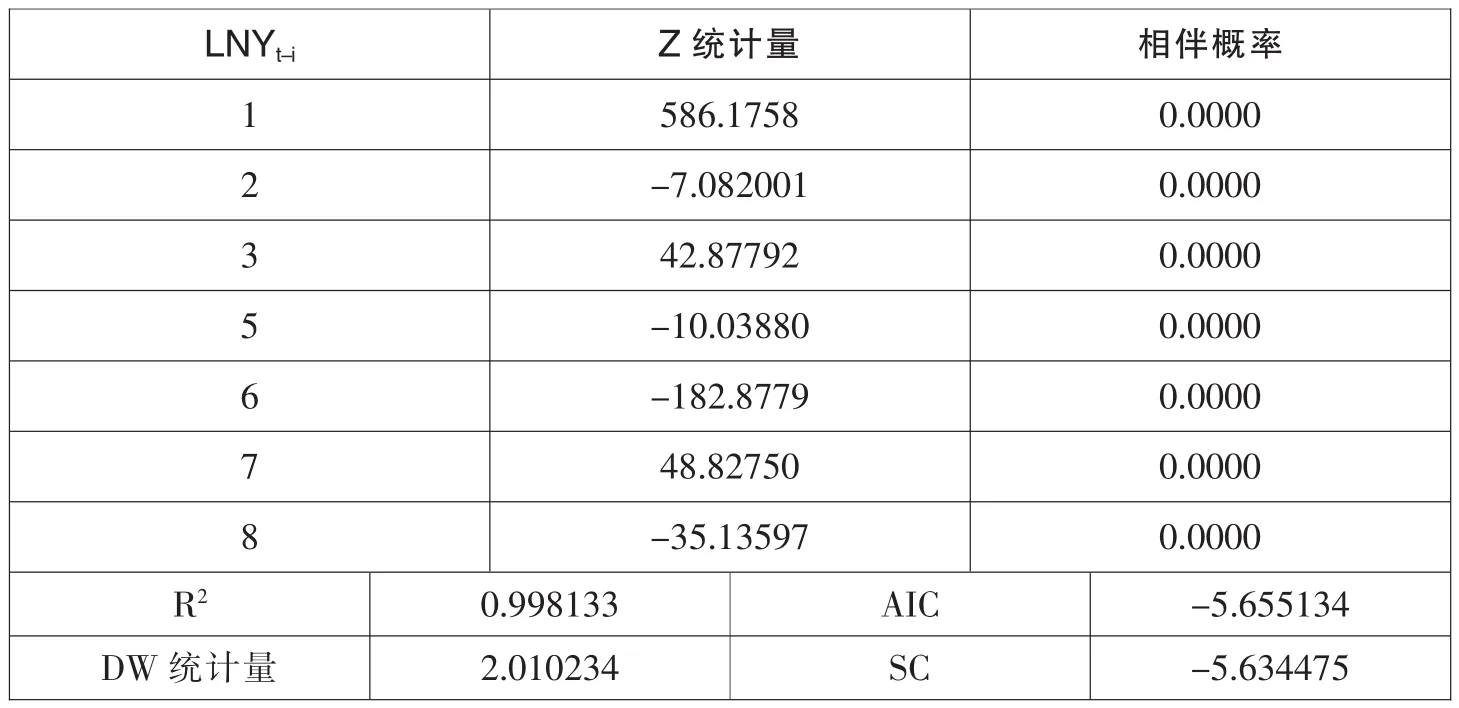
表12 EGARCH（1，1）模型的估计结果

可以看出，模型估计结果的各项指标都通过检验。模型的残差序列自相关结果如表13所示。

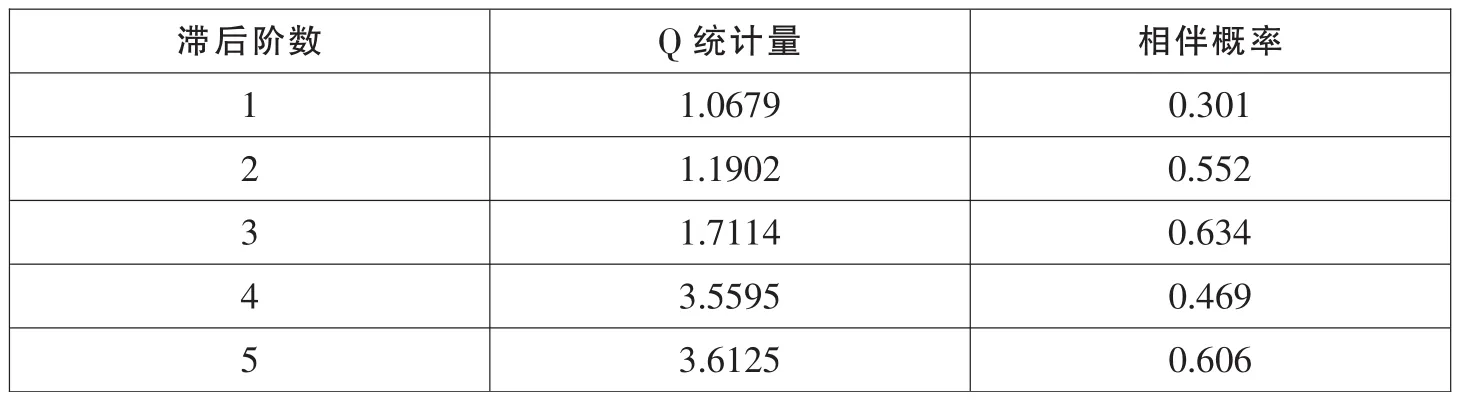
表13 EGARCH（1，1）模型的残差序列自相关结果

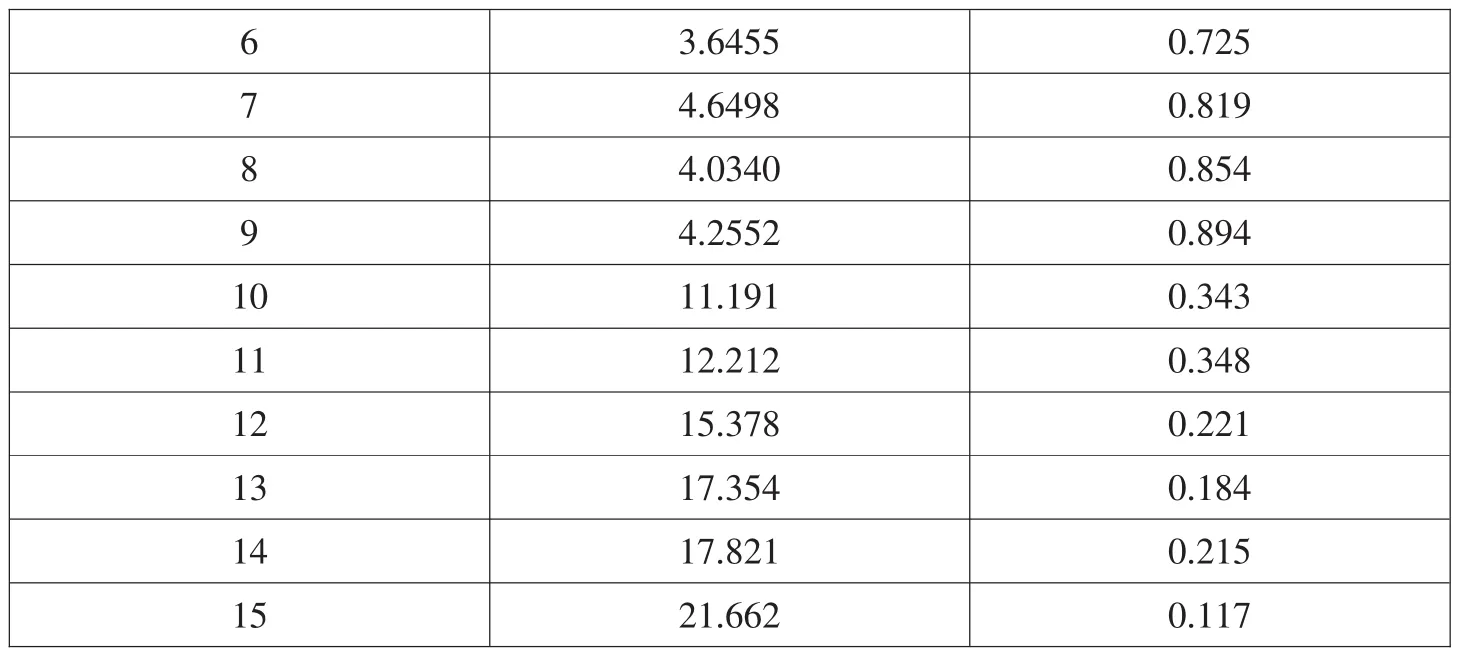
滞后15阶的所有Q值的相伴概率均明显大于0.05，模型的残差项是一个白噪声序列。所以EGARCH（1，1）模型各项指标都通过了显著性检验，对数据拟合较好。

但为尽可能避免模型的拟合优度问题对之后的研究结果造成影响，我们对式（2）（其中 i＝8）再分别建立 TARCH（1，1）模型和 PARCH（1，1）模型。它们的建模过程与EGARCH（1，1）模型的建立过程相同，剔除不显著 LNYt－i项，直到全都通过Z统计量检验，分别得到它们的模型估计结果和残差序列自相关检验结果（表 14、表 15、表 16 和表 17）。

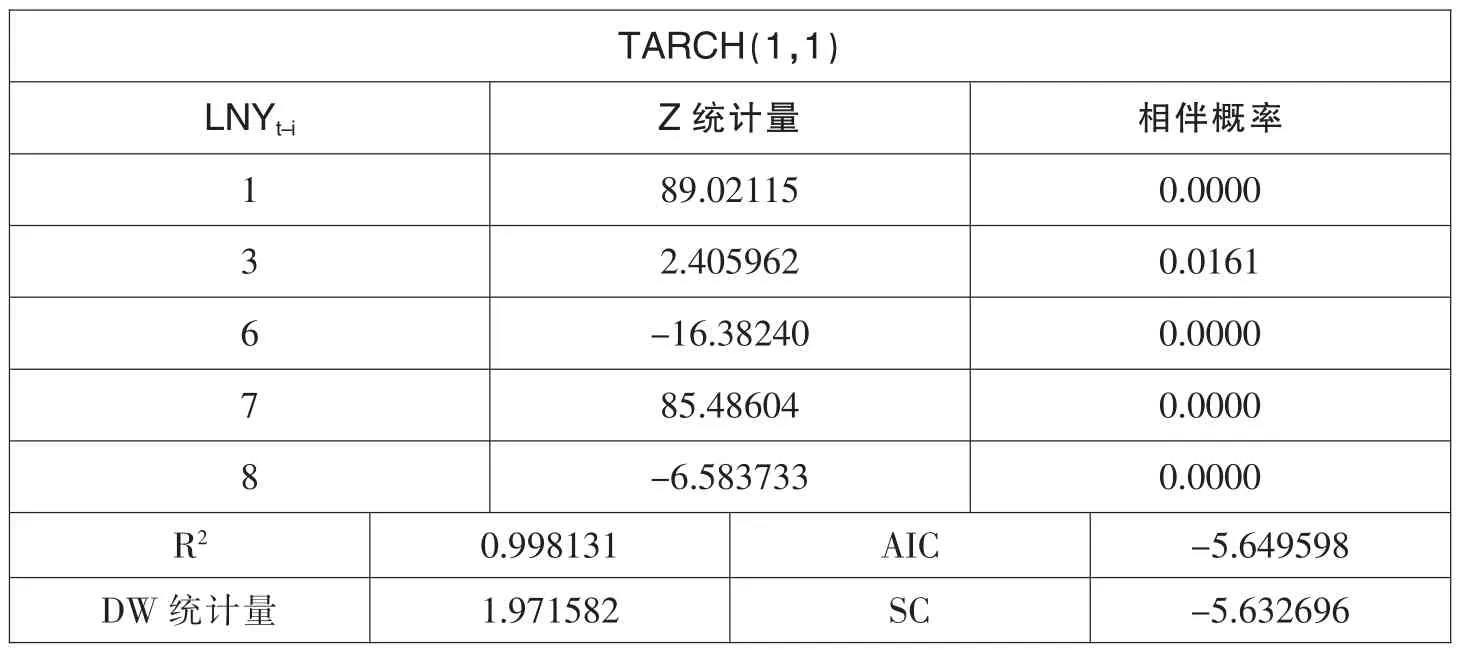
表14 TARCH（1，1）模型的估计结果

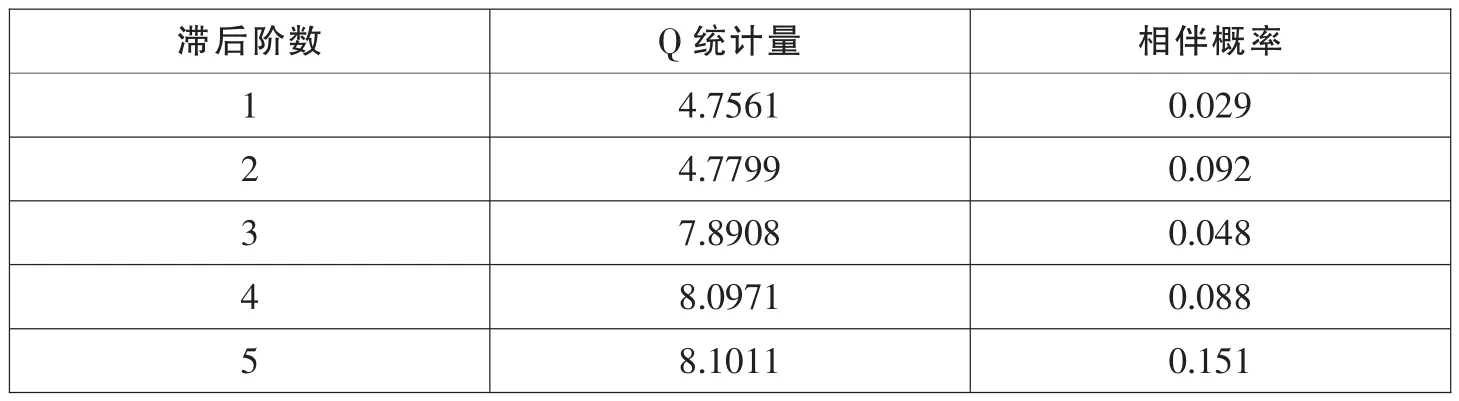
表15 TARCH（1，1）模型的残差序列自相关结果

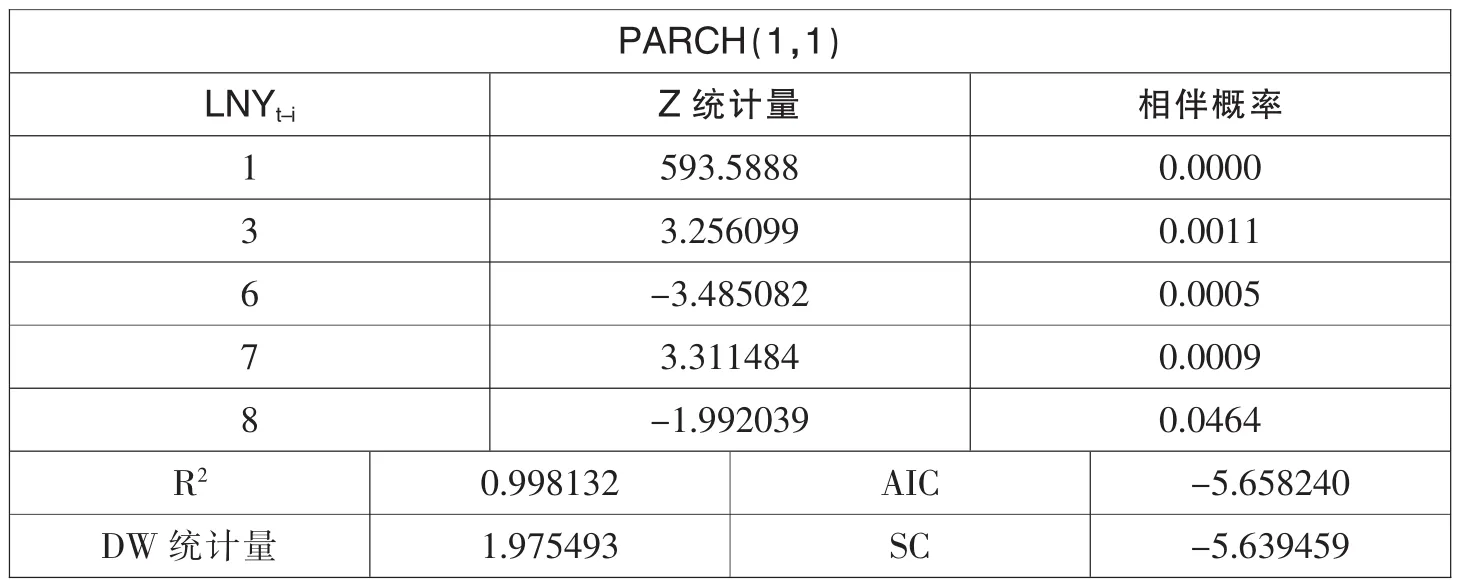
表16 PARCH（1，1）模型的估计结果

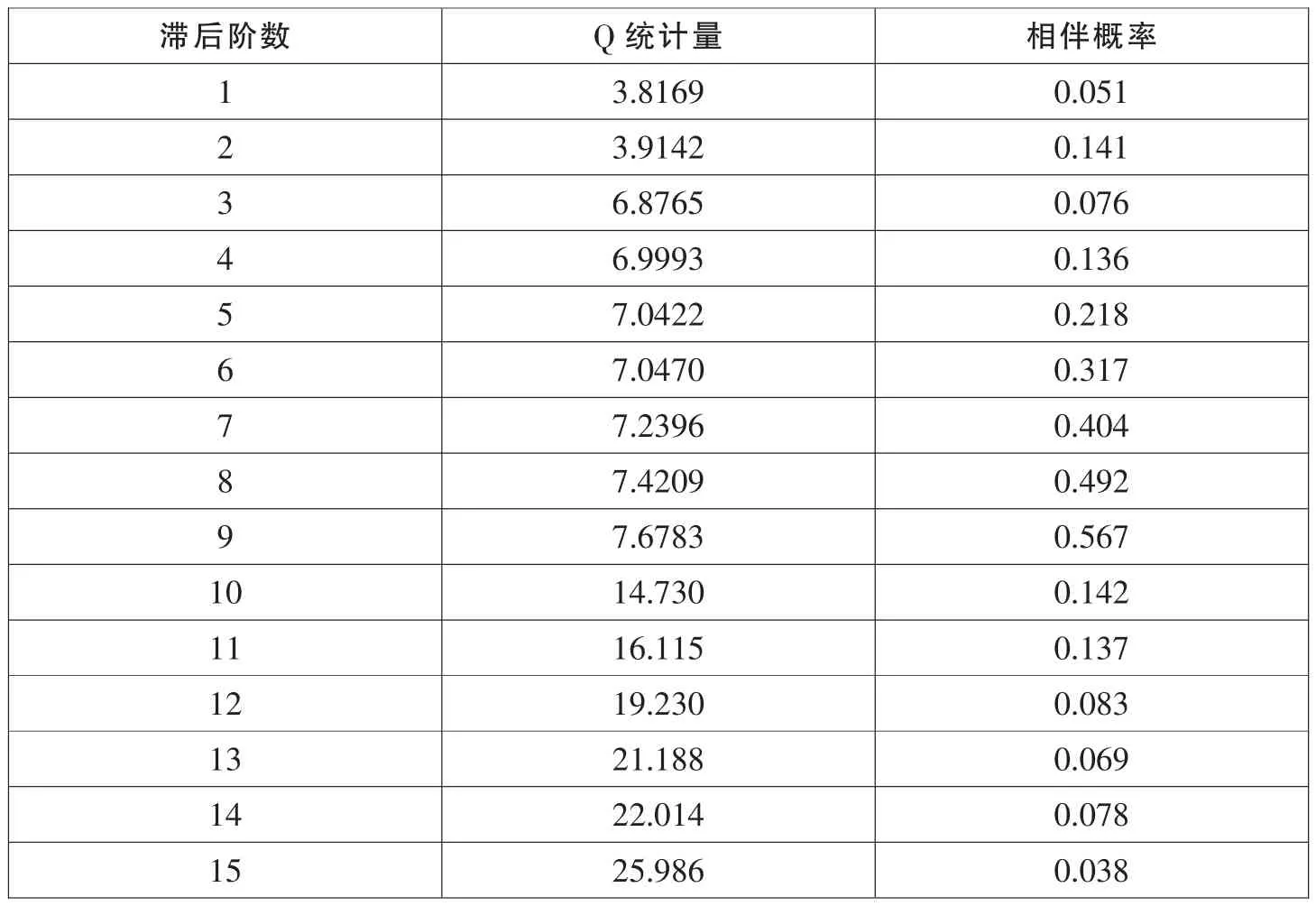
表17 PARCH（1，1）模型的残差序列自相关结果

可以看出，建立的 TARCH（1，1）模型和 PARCH（1，1）模型的均值方程的解释变量都通过了Z统计量检验，但没有EGARCH（1，1）模型拟合得好。并且，它们的残差项都没有通过白噪声的检验。

综上，EGARCH（1，1）模型的各项指标都通过显著性检验，且残差序列是白噪声，信息提取最充分，拟合优度最高。可以认为，对于我们所研究的时间序列｛LNYt｝，EGRACH（1，1）模型为最优模型。它的形式如下。

均值方程：

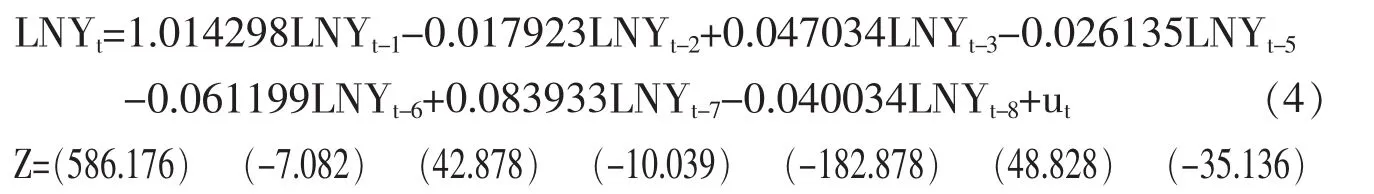
方差方程：

（四）绘制非对称的信息冲击曲线

在 EGARCH（1，1）模型中，α 的估计值为 0.167416，非对称项 γ 的估计值为－0.052729。 当 ut－1＞0 时，即出现“利好消息”时，该信息冲击对条件方差的对数有一个 0.167416＋（－0.052729）＝0.114687 倍的冲击；而当 ut－1＜0，即出现“利空消息”时，该信息冲击对条件方差的对数带来 0.167416＋（－0.052729）＊（－1）＝0.220145倍的冲击。也就是说，印证了前面猜测的序列具有“杠杆效应”，“利空消息”比“利好消息”给中国股票市场带来的冲击更大。

根据模型估计结果，我们绘制出沪市的股票价格收盘指数的信息冲击曲线（如图 3）。

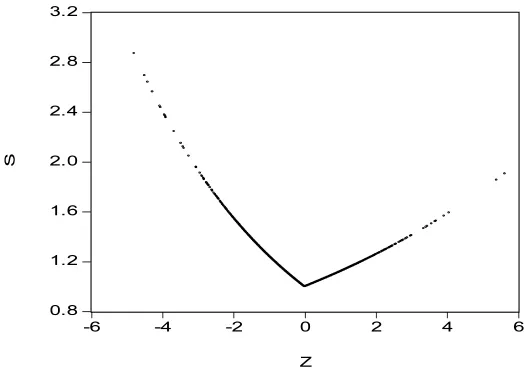
图3 沪市股票价格收盘指数的信息冲击曲线

可以看出，曲线在信息冲击小于0时比较陡峭，而在正冲击时则比较平缓。说明负冲击使得波动性更大一些。

（五）黄金周节前／节后效应检验

建立好EGARCH（1，1）后，为了证实黄金周是否具有节前和节后效应，我们在式（4）中引入虚拟变量D1t和D2t。

值得一提的是，由于自2008年起，五一黄金周被取消，所以从2008年以后的五一黄金周前后的第一个交易日都归为其他交易日。于是模型方程被重新调整，形式如下：

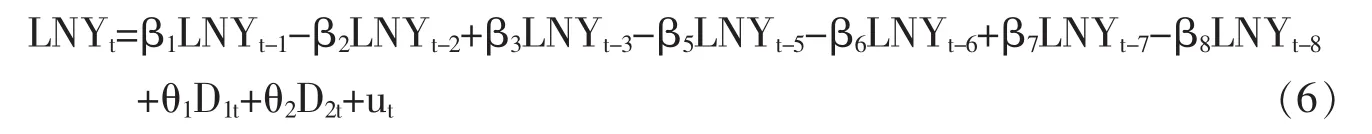
其中θ1和θ2为虚拟变量D1t和D2t的系数，我们只需要对模型进行重新估计，并且检验θ1和θ2是否显著，即可确认黄金周节前效应和节后效应是否存在。

模型的估计结果如表18。

表18 引入虚拟变量后的模型估计结果

可以看出，虚拟变量 D1t的 Z 统计量的绝对值｜Z｜＝1.99＞1.96，说明黄金周节前效应显著存在；而虚拟变量 D2t的｜Z｜＝1.37＞1.96，说明黄金周节后效应不显著。另外，虚拟变量D1t系数为正，这说明黄金周节前对股市波动性具有正向的影响。

（六）黄金周节前效应分析

我们选取2000年6月1日至2013年10月31日所有黄金周节前的第一个交易日相较于前一个交易日的收益率，公式为 Ri＝100＊Ln（Pi／Pi－1），得到 34个样本数据。对该样本数据做柱状图，结果如图4所示。

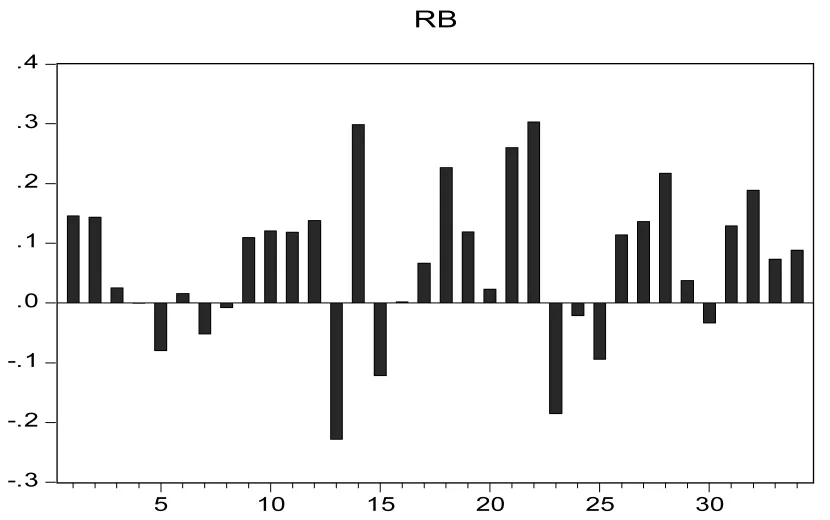
图4 样本数据的柱状图

我们发现，黄金周节前第一个交易日相较于前一个交易日的收益率为正的概率明显高于50%。这与我们通过实证分析得到的结论一致，即存在效应为正的黄金周节前效应。

三、结 论

通过对上证指数的实证研究，发现我国股市存在显著的黄金周节前效应，并且效应为正，不存在节后效应。这印证了理论分析和推断。黄金周的休市往往伴随一些政府的重要政策出台，再加之黄金周旅游拉动各行各业创收，投资者对相关板块的股价持看涨心理。但同时，我国股市存在明显的“杠杆效应”，“利空消息”相较于“利好消息”对股价的冲击更大，说明我国投资者的理性程度不够，常表现出盲目跟风和羊群效应等非理性行为，所以一旦出现不利消息可能会引发加倍的恐慌，从而造成股价迅速下跌。

而黄金周节后效应的不存在，说明节后投资者的心理预期又趋于平时交易日的水平，黄金周对投资者投资行为的影响主要集中在节前，正向的节前效应使得投资者具有套利的可能，但是由于存在“杠杆”，一旦出现“利空消息”或者其他投资者对未来股市普遍持悲观的看跌心理，那么造成损失的风险将比平时更高。因为休市所引起的股价波动异常对于股票市场来说并非一个良好的现象，这说明股票市场并未趋于成熟，还存在许多投机行为。尤其针对我国股票市场来说，如果之前学者研究所发现的“周末效应”与“节日效应”说明我国股市还处于不成熟的初期阶段，那么“黄金周效应”的存在，则说明我国股市还仍旧处在不成熟的发展初期。基于黄金周对我国股市影响的研究，为了使我国股市发展成为一个成熟和有效的市场，我们得出以下两点启示：

（1）提高市场信息公开的透明程度

我国股市的信息公开还不够透明化，投资者往往无法及时得到有效信息。信息的滞后，往往使得投资者错过投资时机，而又存在少数投资者通过特殊渠道获得到有效信息，从而引起市场混乱，乱象频生。

（2）提升投资者自身的投资素质

我国投资者普遍存在两个问题，一是缺乏投资相关的专业知识，二是理性程度不高。投资者的投资行为多为依赖于事件的投机行为，没有从专业的角度对投资标的进行合理地分析和投资。非理性的盲目跟风，没有权衡好利益与风险的关系，往往是投资者亏损的原因。

［1］Wilson J W， Jones C P.Comparison of Seasonal Anomalies across Major Equity Markets： A Note［J］.Financial Review， 1993，28（1）：107－115.

［2］Ryan Chong， Robert Hudson， Kevin Keasey， et al.Pre －holiday Effects： International Evidence on the Decline and Reversal of a Stock Market Anomaly［J］.Journal of International Money and Finance， 2005，（24）：1226－1236.

［3］严太华，孟卫东，杨杰.上海股市 1992－1999 周末效应的实证研究［J］.经济科学，2000，（4）.

［4］田华，陆庆春.上海股市周日效应GARCH模型族的实证研究［J］.系统工程理论与实践，2003，（7）.

［5］义垂林，刘淄.上海股市法定节日及传统节日效应的实证研究，财经科学，2005.

［6］陆磊，刘思峰.中国股票市场具有“节日效应”吗［J］.金融研究，2008，（2）.

［7］王垒，郑小平，施俊琦，等.中国证券投资者的投资行为与个性特征［J］.心理科学，2003，（1）.