Biharmonic Spacelike Submanifolds in Lorentzian Product Space n(c)× R1
LIU Jiancheng, SU Anle
(College of Mathematics and Statistics, Northwest Normal University, Lanzhou 730070, Gansu)
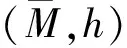
for any compact subsetΩofM. Using the first variational formula (due to G. Y. Jiang, see [2]) one sees thatφis a biharmonic map if and only if its bitension field vanishes identically, i.e.
τ2(φ):=△φτ(φ)-
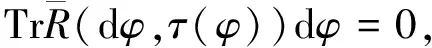
(1)
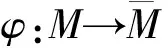
It is well known fromτ(φ)=mHthat an isometric immersion is minimal (|H|=0) if and only if it is harmonic (τ(φ)=0). So a minimal submanifold is trivially biharmonic, and we call a nonharmonic biharmonic submanifold a proper biharmonic submanifold.
The study of proper biharmonic submanifolds is nowadays becoming a very active subject and its popularity was initiated with the challenging conjecture of B. Y. Chen[3]: Any biharmonic submanifold in the Euclidean space is minimal. Due to some nonexistence results (see [4-5]) the Chen conjecture was generalized to (see [6]): Any biharmonic submanifold in a Riemannian manifold with non-positive sectional curvature is minimal. A. Balmus, S. Montaldo, C. Oniciuc, R. Caddeo and E. Loubeau et al. had studied the biharmonic submanifolds in many general aspects, and got some classification results (see [7-9] and the references therein).

Another class of interesting pseudo-Riemannian manifolds is that of Lorentzian product manifoldsn(c)×R1, withn(c) ann-dimensional Riemannian manifold with constant sectional curvaturecandR1one-dimensional pseudo-Riemannian space with a metric -dt2. These spaces play an important role in the general relativity, see, for example, [12-14].
This paper studies biharmonic spacelike submanifolds in Lorentzian product manifoldsn(c)×R1. We first prove an invariant biharmonic equation in Section 2 for such submanifolds in general pseudo-Riemannian manifolds (see Theorem 1). Then we apply it to Lorentzian product manifoldsn(c)×R1, and obtain a key Theorem (see Theorem 2), which gives a sufficient and necessary condition for spacelike submanifolds with parallel mean curvature vector fields to be a biharmonic ones. As a result, we prove some nonexistence theorems for proper biharmonic spacelike submanifolds or hypersurfaces (see Corollaries 4, 5). These all corollaries can be viewed as the dual of their Riemannian version.
1 Preliminaries
In this section, we recall some basic notations and facts concerning Lorentzian product space, tension field of an isometric immersion, that will appear along the paper.

From now on, we consider a special Lorentzian product spacen(c)×R1, withn(c) be ann-dimensional Riemannian manifold with constant sectional curvaturec. For simplicity, we just writen(c)×R1. For anm-dimensional immersed submanifoldΣminif the induced metric viaφonΣmis positive definite, then we callΣma spacelike submanifold ofSet

∂t=T+N,
(2)
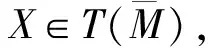
〈π*X,π*Z〉〈π*Y,π*W〉}=
c{〈Y,Z〉〈X,W〉+〈Y,∂t〉〈∂t,Z〉〈X,W〉+
〈Y,Z〉〈X,∂t〉〈∂t,W〉-〈X,Z〉〈Y,W〉-
〈X,∂t〉〈∂t,Z〉〈Y,W〉-〈X,Z〉〈Y,∂t〉〈∂t,W〉}.
Therefore, we obtain
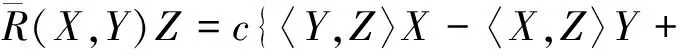
〈Y,∂t〉〈∂t,Z〉X+〈Y,Z〉〈X,∂t〉∂t-
〈X,∂t〉〈∂t,Z〉Y-〈X,Z〉〈Y,∂t〉∂t}.
(3)
⊕νΣm.
(4)
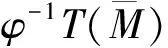
dφ(XY)=B(X,Y),
(5)
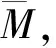

(6)
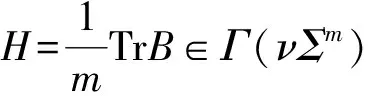
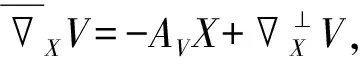
2 Main results and its proofs

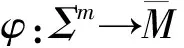
(7)
whereAdenotes the shape operator,Bthe second fundamental form,Hthe mean curvature vector field, and⊥, △⊥the normal connection and the Laplacian on the normal bundle ofΣminrepectively.

(8)
Also
△⊥H-TrA(·)-
TrB(·,AH·)-Tr(·)AH(·).
(9)
Tr(·)AH(·)=
(10)
Meanwhile
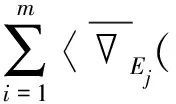
Substituting (11) into (10), we have
which, together with (9), yields that
△φH=△⊥H-2TrA(·)-
(12)
Finally, putting (12) into (8) and collecting all the tangent and normal parts of the bitension field separately, we complete the proof of Theorem 1.
Remark1Except the squared norm |H|2of the mean curvature vector fieldHis a minus one whenHis timelike, the biharmonic equation (7) coincides with that in Riemannian case formally (cf. Theorem 2.1 of [7]). Using moving frame method, Ouyang also obtained a local biharmonic equation for spacelike submanifolds in pesudo-Riemannian manifolds, we refer readers to Proposition 3.1 of [10].
Theorem2A PMC spacelike submanifoldΣm,m≥2, in Lorentz product spacen(c)×R1is biharmonic if and only if
Moreover, the mean curvature vector fieldHmust be spacelike ones.
ProofFrom (3) we know
(m+|T|2)H-m〈H,∂t〉N}.
Putting into (7), we get
(13)
SinceΣmis a PMC spacelike submanifold, (13) becomes
(14)

for anyX,Y∈Γ(TΣm). Thus 〈H,∂t〉=0 onΣm. It is a contradiction.
Now, we proveH⊥∂tfrom the second equation of (14). Suppose on the contrary that there exists a pointp∈Σmsuch that 〈H,∂t〉(p)≠0, and then 〈H,∂t〉≠0 on a neighborhood(p) ofp, soT|=0. This fact together with (2) leads to 〈X,∂t〉=0 on(p) for any vector fieldX∈Γ(TΣm). On the other hand, because ofwe get
for anyX,Y∈Γ(TΣm). Thus 〈H,∂t〉=0 on the neighborhood(p), which is a contradiction. Consequently, we haveH⊥∂teverywhere onΣm.
According to the conclusionH⊥∂t, the first equation of (14) reduces to
TrB(·,AH·)=c(m+|T|2)H.
Thus, we obtain
which completes the proof of Theorem 2.
In the following, by using Theorem 2, we shall prove that the tangent part of ∂thas constant length for a proper biharmonic PMC spacelike surface. Also, we shall derive a condition for PMC biharmonic spacelike submanifolds to be the maximal ones and prove a nonexistence result for biharmonic hypersurfaces.
LetΣ2be a biharmonic PMC spacelike surface inn(c)×R1. According to [15], we note that the mapp∈Σ2→(AH-μI)(p), whereμa constant, is analytic and, therefore, eitherΣ2is a pseudo-umbilical surface (at every point), orH(p) is not an umbilical direction for any pointp, orH(p) is an umbilical direction on a closed set without interior points. We denote byWthe set of points whereHis not an umbilical direction. In the second case,Wcoincides withΣ2, and in the third one,Wis an open dense set inΣ2.
Corollary3IfΣ2is a proper biharmonic PMC spacelike surface inn(c)×R1, then the tangent partTof ∂thas constant length.
ProofIt follows from Theorem 2 that 〈H,∂t〉=0, which implies
for any tangent vector fieldX, thenAHT=0.
If the surface is pseudo-umbilical, i.e.,AH-|H|2I=0, then we have 0=AHT=|H|2T, i.e.,T=0.
Now, assume thatΣ2is non-pseudo-umbilical, and we shall work onWdefined above. Taking similar observation as done in Lemma 1 of [19], at any point inW, there exists a local orthonormal frame field that diagonalizesAUfor any normal vector fieldUdefined onW. So we can consider {E1,E2} an orthonormal basis at an arbitrary pointp∈Wthat diagonalizesAHandAN. It follows from Theorem 2 thatH⊥∂tand |AH|2=c(2+|T|2)|H|2, furthermore,H⊥N. Hence we have TrAN=2〈H,N〉=0. The matrices ofAHandANwith repect to {E1,E2} are
Moreover

Corollary4Suppose thatΣmbe a PMC biharmonic spacelike submanifold inn(c)×R1. Ifc≤0 or ‖B‖2<(m+|T|2)c, then |H|=0, i.e.Σmis a maximal.
ProofSinceΣmbe a PMC biharmonic spacelike submanifold, we know from Theorem 2 that
|AH|2=c(m+|T|2)|H|2.
(15)

Whenc<0 and by Theorem 2, 〈H,∂t〉=0.His a spacelike vector field, the right hand side of (15) is non-positive, the conclusion is obvious.
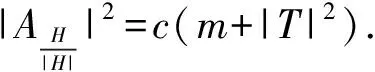
Moreover, we get
(m+|T|2)c≤‖B‖2<(m+|T|2)c,
i.e., (m+|T|2)c<(m+|T|2)c, which is a contradiction. Consequently, |H|=0, and we end the proof of Corollary 4.
Corollary5There exist no nonminimal biharmonic spacelike hypersurfaces with constant mean curvature inn(c)×R1.
ProofFor a biharmonic spacelike submanifold inn(c)×R1with constant mean curvature, Theorem 2 tells us that its mean curvature vectorHis a spacelike one, so Corollary 5 follows immediately.
致谢甘肃省高等学校基本科研业务费对本文给予了资助,谨致谢意.
[1] Eells J, Sampson J H. Harmonic mappings of Riemannian manifolds[J]. Am J Math,1964,86:109-160.
[2] 姜国英. 2-调和映照及其第一、第二变分公式[J]. 数学年刊,1986,A7(4):389-402.
[3] Chen B Y. Some open problems and conjectures on submanifolds of finite type[J]. Soochow J Math,1991,17(2):169-188.
[5] Caddeo R, Montaldo S, Oniciuc C. Biharmonic submanifolds in spheres[J]. Israel J Math,2002,130:109-123.
[6] Caddeo R, Montaldo S, Oniciuc C. Biharmonic submanifolds of3[J]. Internat J Math,2001,12(8):867-876.
[8] Liu J C, Du L. Biharmonic submanifolds inδ-pinched Riemannian manifolds[J]. J Math Research & Expo,2010,30(5):891-896.
[9] Montaldo S, Oniciuc C. A short survey on biharmonic maps between Riemannian manifolds[J]. Revista de La Unión Matemtica Argentina,2006,47(2):1-22.
[10] 欧阳崇珍. 伪黎曼空间型的2-调和类空子流形[J]. 数学年刊,2000,A21(6):649-654.
[11] Zhang W. Biharmonic space-like hypersurfaces in pseudo-Riemannian space[J/OL]. arXiv:0808.1346v1,2008.
[12] Albujer A L. New examples of entire maximal graphs in2×R1[J]. Diff Geom Appl,2008,26(4):456-462.
[13] Albujer A L, Alías L J. Calabi-Bernstein results for maximal surfaces in Lorentzian product spaces[J]. J Geom Phys,2009,59(5):620-631.
[14] Albujer A L, Camargo F E C, de Lima H F. Complete spacelike hypersurfaces with constant mean curvature in -R×n[J]. J Math Anal Appl,2010,368(2):650-657.
[15] Fetcu D, Oniciuc C, Rosenberg H. Biharmonic submanifolds with parallel mean curvature inn×R[J]. J Geom Anal,2013,23(4):2158-2176.
[16] Kobayashi S, Nomizu K. Foundations of Differential Geometry[C]//Pure and Applied Mathematics. New York:Wiley,1969:15.
[17] Baird P, Wood J C. Harmonic Morphisms between Riemannian Manifolds[C]//London Mathematical Society Monographs. Oxford:Oxford University Press,2003:29.
[18] Chen B Y. Pseudo-Riemannian Geometry,δ-Invariants and Applications[M]. New Jersey:World Scientific Publishing,2011.
[19] Alencar H, do Carmo M, Tribuzy R. A Hopf theorem for ambient spaces of dimensions higher than three[J]. J Diff Geom,2010,84:1-17.

