半刚性有侧移组合框架柱计算长度系数研究
邹国强,周 超
(1.深圳市欧博工程设计顾问有限公司,广东深圳 518053;2.华南理工大学土木与交通学院,广东广州 510640)
全刚性连接或理想铰接的假定使钢结构分析和设计过程大大简化,但现实工程中大多数的梁柱连接所具有的刚度介于全刚性和理想铰接之间,为半刚性连接。传统的设计方法并没有考虑楼板对梁柱连接的影响,其实由于栓钉的连接使得梁和楼板协调工作,这在很大程度上增加了节点的承载力和转动刚度。因此,在进行梁柱分析时应考虑楼板的影响[1-3],这与实际工程情况一致。
本文在纯钢半刚性节点的基础上考虑了楼板的组合效应,把钢结构规范中刚接框架柱的稳定设计方法用于半刚性的柱的稳定设计,推导了有侧移半刚性钢框架柱的有效长度系数计算方程。最后用1个实例探讨了不同螺栓排列对梁柱平齐端板连接框架柱的有效计算长度系数的影响。
1 连接刚度计算
1.1 连接的初始转动刚度
为了计算梁柱半刚性连接的初始转动刚度,欧洲规范EC3[4]提出了组件法用来计算纯钢节点的初始刚度,文献[5]提出了一种半刚性节点初始刚度组件式计算模型。对于组合节点则是增加了楼板这一组件对刚度的影响,如图1是在负弯矩作用下组合节点初始转动刚度计算模型。文献[6]对初始刚度的计算做了详细的介绍。连接的初始转动刚度为
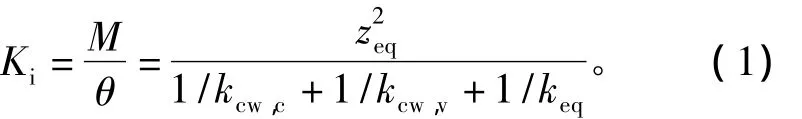
式中:zeq为受力形式相同但不同高度组件的等效力臂;keq为与zeq相对应的等效刚度;kcw,v为柱腹板的抗剪刚度;kcw,c为柱腹板的抗压刚度。
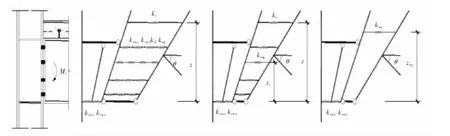
图1 组合节点初始转动刚度计算模型Fig.1 Initial stiffness model of composite joints
1.2 有效割线刚度
节点的非线性弯矩-转角关系模型,采用三参数幂函数模型[7]:
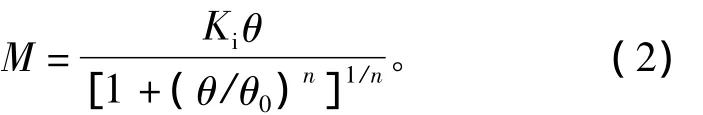
式中:θ0为与连接的极限弯矩Mu对应的初始塑性转角,θ0=Mu/Ki;n为形状参数。
连接有效割线刚度是钢架横梁作用于如图2所示竖向荷载时与端弯矩Me所对应的割线刚度。
梁的转角位移方程为
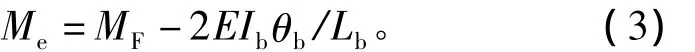
式中:MF为刚接时梁端弯矩,MF=qL2b/12;θb为节点转角。
用解析法由式(2)和式(3)联立可求得端弯矩Me和转角θb,从而得到连接的有效割线刚度,其表达式为Ke=Me/θb。
2 梁刚度及修正系数
2.1 组合横梁的抗弯刚度
对于组合梁,由于要考虑楼板混凝土和钢筋在不同弯矩情况下对组合梁刚度的贡献,所以横梁的刚度在梁端和跨中是不一样的,故对梁的刚度应做等效处理。为了方便设计,采用AMMERMAN等建议的等效组合梁截面惯性矩计算方法[8]:
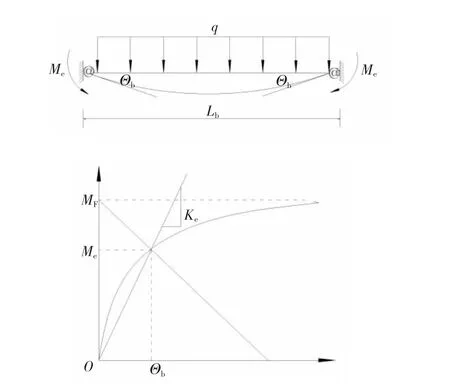
图2 连接的有效割线刚度Fig.2 Effective secant stiffness of the connection

式中:I1为组合梁正弯矩区的惯性矩,考虑了混凝土及滑移效应对组合梁刚度的影响;I2为负弯矩区的惯性矩,考虑了钢筋的影响。具体的计算可以参考文献[6]。组合梁的抗弯刚度由钢梁的弹性模量E和等效截面惯性矩Ib的乘积表示。
2.2 横梁刚度修正系数
对横梁的假定:1)梁均为弹性等截面;2)不计横梁轴力的影响;3)框架屈曲时,同一层梁两端的转角大小相等且同方向。
如图3所示,横梁的梁端为半刚性连接。KeA,KeB是梁连接刚度等于屈曲时的有效割线刚度。梁端的转角位移方程为
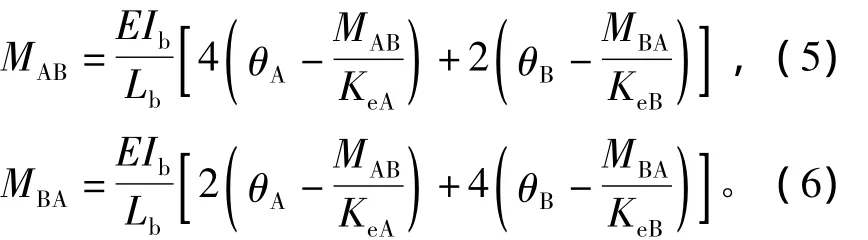
由式(5)和式(6)可以求得
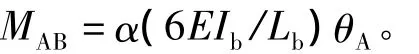
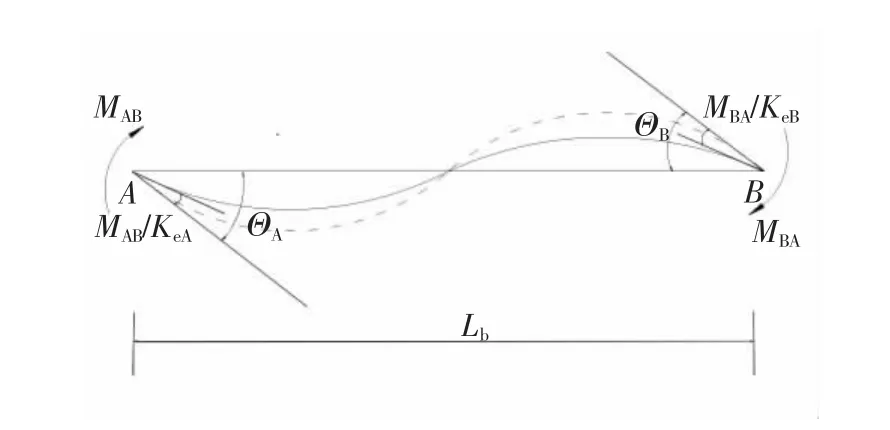
图3 半刚性连接梁端弯矩Fig.3 Semi-rigid beam-end moment
3 柱的有效长度系数计算
利用三层框架柱模型计算柱的长度系数,假定框架中的杆件均为弹性等截面,各层柱与其相连的柱同时屈曲,各柱的稳定函数相等。在图4中柱C1和柱C3的远端为刚接。

图4 柱长度计算单元Fig.4 Column length element
建立梁柱的转角-位移方程,在根据柱C2两端节点的平衡方程和变形协调方程建立柱的计算长度的方程。具体的计算可参照文献[9],柱的有效长度方程式为
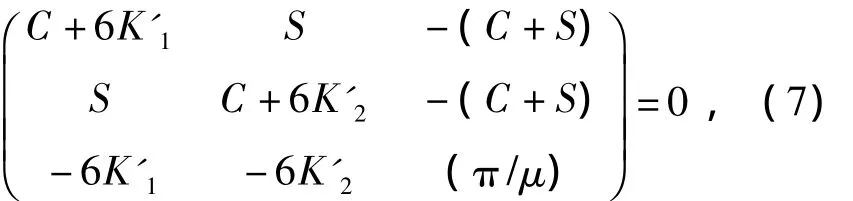
式中C和S为稳定函数。
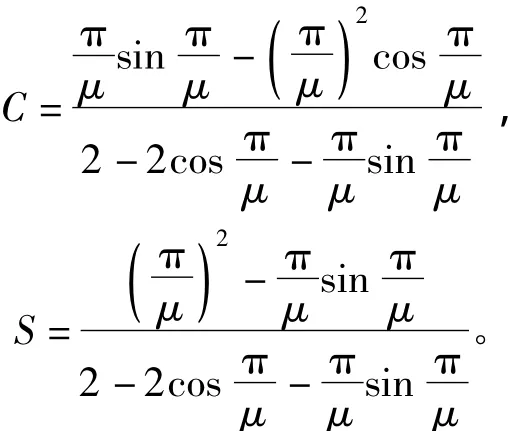
将C和S代入有效长度的计算方程式,最终化简为
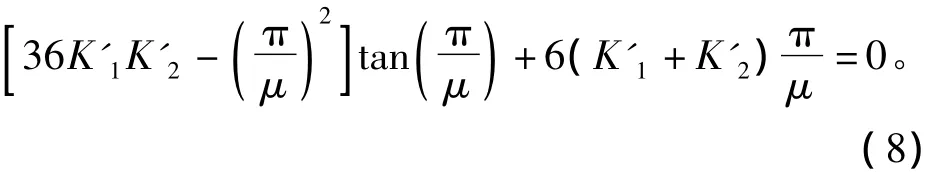
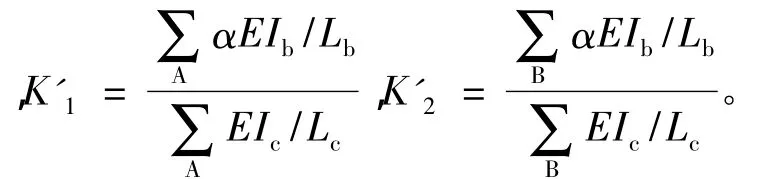
此方程与GB 50017—2003规范[10]附录D表中的公式相近,只是用K'1,K'2代替K1,K2。
4 平齐端板连接算例
如图5所示平齐端板梁柱组合节点框架实例,钢梁尺寸为HN300 mm×150 mm×6.5 mm×9 mm,钢柱尺寸为 HW250 mm×250 mm×10 mm×14 mm,平端板的尺寸为330 mm×200 mm×14 mm,柱的腹板设有加劲肋,钢材为Q345,螺栓10.9级,采用钢-混凝土的组合楼盖,纵向受力钢筋等级为HRB335,混凝土强度等级C30,采用压型钢板,压型钢板波高75 mm,波距230 mm,现浇140 mm厚混凝土。均布荷载45 kN/m是正常使用荷载。
本文以平齐端板梁柱组合节点框架为例,用本文的计算方法和精确方法计算柱的计算长度系数。精确计算方法是直接由式(7)计算,其对柱C1和柱C3远端约束无任何限制。在满足螺栓构造要求的基础下,改变螺栓间距,螺栓排列如图6所示,计算结果如表1所示。
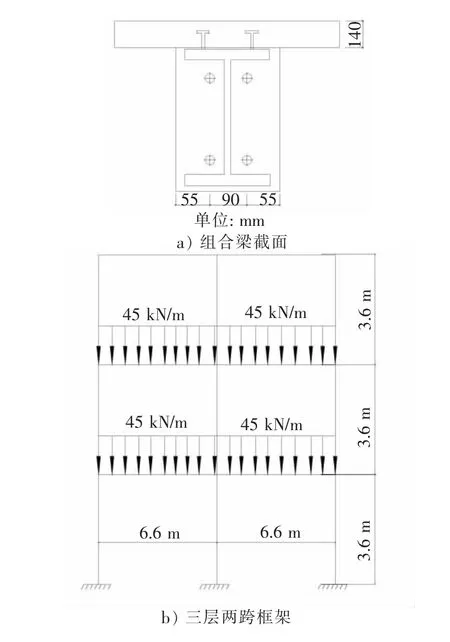
图5 组合框架实例Fig.5 Examples of composite frames
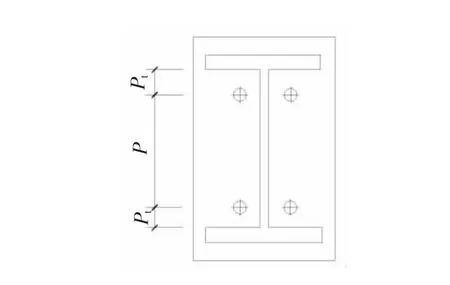
图6 螺栓的排列图Fig.6 Pareto diagram of the bolt
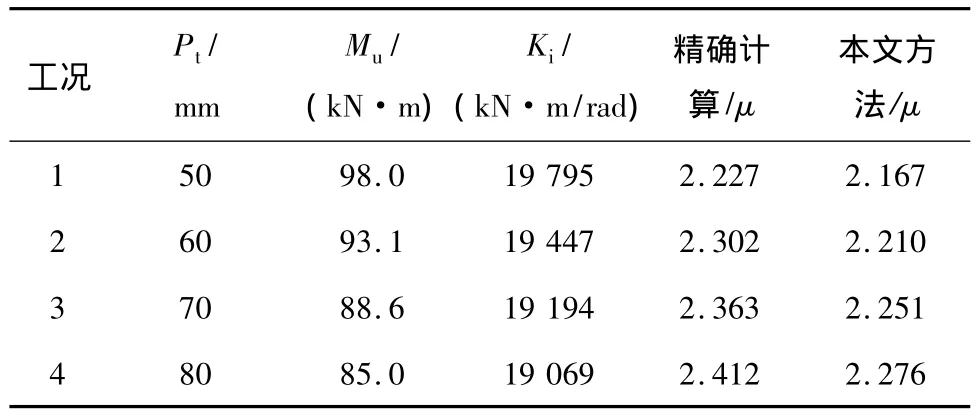
表1 有侧移框架柱C2的计算长度系数Tab.1 Effective length factor of column C2 for composite frames with sidesway
由表1知本文简化计算方法和精确计算方法得到的框架柱的长度系数误差相对不是很大,误差范围在5%左右,可以用本文的计算方法计算组合框架柱的长度系数。如果按刚接设计节点,由GB 50017—2003查柱的计算长度系数μ=1.32,这对于实际结构的设计偏于不安全。
5 结论
1)利用Barakat-chen法推导了有侧移半刚性梁柱组合框架的柱计算长度系数方程,其形式与钢结构规范的计算公式相似,只是对梁的刚度进行了组合以及整体的修正。
2)利用纯钢结构柱的计算方法推导出组合框架柱的计算长度系数公式,与精确计算的方法较接近,可用于有侧移半刚性连接组合框架稳定分析和设计。
3)对于比较明显的半刚性连接设计,应对梁的刚度进行修正,再计算柱的计算长度系数,而不是以刚接形式由规范查表得到,这是偏于不安全的。
/References:
[1] EDUARDO B,JAVIER G,BEATRIZ G,et al.An efficient cruciform element to model semirigid composite connections for frame analysis[J].Journal of Constructional Steel Research,2012,72: 97-104.
[2] VASDRAVELLIS G,UY B,TAN E L,et al.Behaviour and design of composite beams subjected to negative bending and compression[J].Journal of Constructional Steel Research,2012,79: 34-47.
[3] BEATRIZ G,RUFINO G,EDUARDO B.Experimental and numerical validation of a new design for three-dimensional semi-rigid composite joints[J].Engineering Structures,2013,48:55-69.
[4] Eurocode3,Design of Steel Structures[S].
[5] 王振宇,张劲帆,方 成,等.半刚性节点初始刚度的组件式计算模型[J].浙江大学学报(工学版),2012,46(11): 1998-2006.
WANG Zhenyu,ZHANG Jinfan,FANG Cheng.Study on the component-based model of semi-rigid joints[J].Journal of ZhejiangUniversity(Engineering Science), 2012, 46(11): 1998-2006.
[6] 李国强,石文龙,王静峰.半刚性连接钢框架结构设计[M].北京:中国建筑工业出版社,2009.
LI Guoqiang,SHI Wenlong,WANG Jingfeng.Design of Steel Frames with Semi-Rigid Connections[M].Beijing:China Building Industry Press,2009.
[7] KISHIN N,CHEN W F.Moment-rotation relations of semi-rigid connections with angles[J].Journal of Structural Engineering ASCE,1990,116(7):1813-1834.
[8] AMMERMAN D J,LEON R.Unbranced frames with semi-rigid composite connections[J].Engineering Journal AISC,1990,27 (1):1-10.
[9] 杨文惠,王 燕.半刚接钢框架柱的稳定分析方法[J].钢结构,2005,20(3):21-24.
YANG Wenhui,WANG Yan.The stability analysis of columns for steel frames with semi-rigid connecions[J].Steel Construction,2005,20(3):21-24.
[10] GB 50017—2003,钢结构设计规范[S].
GB 50017—2003,Code for Design of Steel Structures[S].

