考虑管路的飞机液压刹车系统压力振荡分析

黄 澄 焦宗夏 尚耀星

(北京航空航天大学 自动化科学与电气工程学院，北京 100191)

由于液压刹车系统具有响应速度快、负载刚度大、终端功率密度大和技术成熟度高等优点，仍广泛用于为飞机提供制动能量.压力伺服阀能输出与控制信号成正比的压力，具有较高的频响，适合于直接的压力控制，因此通常采用压力伺服阀作为液压刹车压力控制元件.飞机液压刹车系统能否正常工作是保证飞机安全的重要因素.然而飞机液压刹车系统在调试、使用过程中，经常会出现压力控制振荡、失稳的现象，并引起管路振动，甚至导致管路破裂的事故［1］.针对这个问题目前并没有理论上的分析，实际中也往往只是通过经验性的调整参数来避免.

传统的飞机液压刹车系统建模与防滑控制算法设计中，通常会忽略压力伺服阀本身压力闭环的特性和伺服阀与刹车作动器之间管路的特性［2－4］，甚至忽略刹车压力建立的动态过程，而简单地认为压力伺服阀能理想地输出给定的压力，并且阀出口的压力即等于实际作动器处的刹车压力.这些假设在压力伺服阀、管路和作动器整体匹配设计的条件下是合理的.但是事实上，飞机液压刹车系统阀和作动器之间存在的刹车管路，会给系统引入欠阻尼的特性，而且该特性会与压力伺服阀固有的局部压力闭环结构相耦合，使得压力伺服阀的输出压力容易出现振荡、失稳现象.如果忽略了这些因素，则无法找到飞机液压刹车系统压力振荡的原因.近些年，有越来越多的研究开始分析管路对阀控电液系统的影响［5－6］，但是针对飞机液压刹车系统的分析仍属空白.

本文针对传统的基于压力伺服阀的防滑刹车系统，通过在建模中考虑阀后管路模型，具体分析了压力伺服阀局部压力闭环与刹车管路耦合，造成阀输出压力容易控制失稳的现象和原因，同时分析了管路和油液等参数对压力控制的影响，并列出了几种避免压力振荡、失稳的方法，仿真分析比较了它们的优劣.

1 飞机液压刹车系统模型

忽略备份和次要元件，建立飞机液压刹车系统中压力伺服阀、刹车管路及刹车作动器的模型.系统构成图如图1所示.

图1 飞机液压刹车系统构成图

常用的压力伺服阀为两级结构，先导级通常为力矩马达控制的喷嘴-挡板或者射流管，二级为滑阀，并通过内部油道将输出负载压力反馈到滑阀阀芯，构成油液的压力闭环［7］.由于压力伺服阀先导级的动态响应较高，为了简化分析将其近似为一个比例环节，即假设先导级作用于滑阀阀芯的控制力Fp与控制信号U成正比:

其中Kt为控制信号先导级输出力系数.滑阀阀芯运动方程［8］为

其中，xv为滑阀阀芯位移;wv，ξ与Kv分别为滑阀阀芯运动的固有频率、阻尼比和等效弹簧刚度;Pv为阀出口压力;Af为阀出口压力对滑阀阀芯的反馈作用面积.

压力伺服阀出口流量可由如下线性化方程求得

其中Kq和Kp分别为滑阀的流量增益与流量压力系数.

其中，Cq为流量系数;W为湿周;ρ为油液密度.

因为对于压力闭环系统，处于某压力工作点时阀芯位移为零，所以可取线性化工作点为(0，Pe)，Pe代表某工作压力，则式(3)可进一步简化为

对于阀后至刹车作动器的液压刹车管路，可假设其为刚性管，且其中油液为层流，则该管路进、出口处油液动态可表示为拉式空间中的二端口模型［9］:

该模型包含无限维的贝塞尔函数，可用于精确分析管路的频率特性，式中特征阻抗Z(s)和传播算子Г(s)由油液黏度和管路尺寸决定，分别表示如下:

其中，c为油液中波速;r为管路内部半径;L为管路长度;J0和J1分别为零阶和一阶一类贝塞尔函数;υ为油液动力黏度.

对于刹车作动器，由于其行程较小，忽略其活塞运动的动态过程，则刹车容腔处压力Pb可由如下方程表示:

其中cb为刹车作动器等效压力容积系数.

2 液压刹车系统压力闭环问题分析

根据所建模型，对飞机液压刹车系统的压力闭环进行频域特性分析.

将上述模型中式(8)进行拉式变换，并结合式(6)，可以得到压力伺服阀出口流量到出口压力的传递函数G(s):

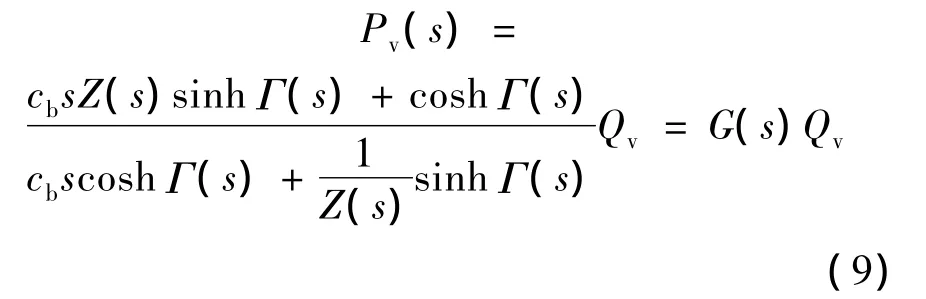
再将式(2)进行拉式变换，结合式(1)和式(9)，可得飞机液压刹车系统中基于压力伺服阀的压力闭环控制框图，如图2所示.图2中并没有包括Pv-Pb的传递函数，因为刹车作动器中压力Pb并不在压力闭环中.而且由于使用压力伺服阀，液压刹车系统的压力闭环参数主要由压力伺服阀本身流量增益Kq和滑阀阀芯反馈台肩面积Af决定，设计中调节范围有限，且加工完成后即难以调整.

图2 压力伺服阀刹车系统压力闭环控制框图

另外，从图2中可知，压力伺服阀滑阀动态是典型的二阶环节，而阀出口流量Qv到阀出口处压力Pv的传递函数则是该闭环中的关键环节，其特性主要取决于管路长度、内径和油液的弹性模量、黏度等参数.给定一组参数值，见表1.

通过绘制Qv-Pv传递函数的伯德图可以定性地分析该环节对系统压力闭环的影响，如图3所示.

表1 液压刹车系统仿真参数

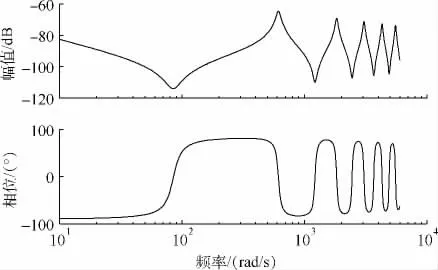
图3 液压刹车系统压力闭环Q v-P v传递函数伯德图

由图3可知，该传递函数随频率增加交替出现欠阻尼的谐振峰和反谐振峰，而且谐振峰幅值远大于低频段幅值.这些欠阻尼的谐振峰在特定的频段上给系统压力闭环带来了很大的开环增益，参数选取不当时将大大降低系统闭环的稳定裕度［10］，从而造成压力控制失稳.

飞机液压刹车系统容易出现压力控制失稳的根本原因可以归结为:阀后存在的管路造成了阀出口压力的频率特性在某些频段上欠阻尼，使得压力伺服阀构成的局部压力闭环稳定裕度不足.

3 频域分析与避免压力振荡的方法

为了避免管路效应与压力伺服阀压力闭环相耦合，本节分析了管路参数和油液参数对Qv-Pv传递函数频率特性的影响，并相应列出了几种避免压力闭环控制振荡失稳的方法.

3.1 管路长度和通径

管路长度对Qv-Pv传递函数的频率特性影响较大.在不改变表1中其他参数的条件下，分别取管路长度为2，3和4m，Qv-Pv传递函数的伯德图如图4所示.

图4 不同管路长度下Q v-P v传函伯德图

由图4可知:随着管路的增长，谐振峰和反谐振峰的谐振频率都逐渐降低，谐振峰值略微降低;当管路长度达到3m时，第1个谐振峰的频率约为600 rad/s，已经接近常用的压力伺服阀的转折频率.在这种情况下，若伺服阀本身阻尼比较低，则将与管路所带来的谐振峰耦合，使系统稳定裕度进一步降低.因此在实际设计中应尽量令管路容腔负载的谐振峰频率避开压力伺服阀的滑阀级的固有频率.

通过比较管路长度3m和4m时，系统的开环频率特性，可以计算压力闭环的模稳定裕度，如图5所示.管路长4m时系统模稳定裕度约为4 dB，而3m时模稳定裕度为－5 dB.因此对于本文分析的系统，管路增长至4m时要比3m时稳定.但是实际中管路长度往往由飞机整体架构决定，并不能大幅度地改变，因此该方法可调整的范围十分有限.

图5 不同管路长度下系统开环伯德图

管路的通径对系统的频率特性也有一定影响.同样在不改变表1其他参数的条件下，分别取管路通径为4，6和8mm，Qv-Pv传递函数的伯德图如图6所示.

图6 不同管路通径下Q v-P v传递函数伯德图

由图6可知，增大管路通径能在一定程度上降低Qv-Pv传递函数的中高频段幅值，同时只提高了第1个反谐振峰的频率而对其他峰值频率影响较小.因此设计中增加管路通径，对改善系统压力闭环的频率特性有一定益处，但是增加管路通径会增加系统质量，对于机载系统这往往不能接受.

3.2 油液弹性模量和黏度

除了管路相关参数外，油液的特性(弹性模量和黏度)也影响着系统的频率响应.同样通过绘制不同弹性模量和黏度条件下的Qv-Pv传递函数伯德图，如图7和图8所示，可以得到以下结论:

1)油液弹性模量降低会使Qv-Pv传递函数中高频段的谐振和反谐振频率降低;

2)油液黏度降低会增大Qv-Pv传递函数的谐振峰和反谐振峰幅值.

而且值得注意的是，与管路参数为设计定常值不同，油液的特性具有时变性.这就使得液压刹车系统的频率特性会随系统工况而变化，增加了系统的不确定性.设计中需要考虑一定范围工况下的谐振频率的变化.

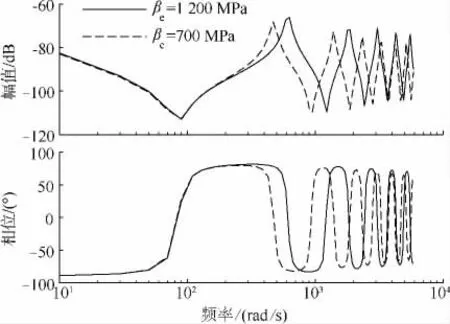
图7 不同油液弹性模量下Q v-P v传递函数伯德图

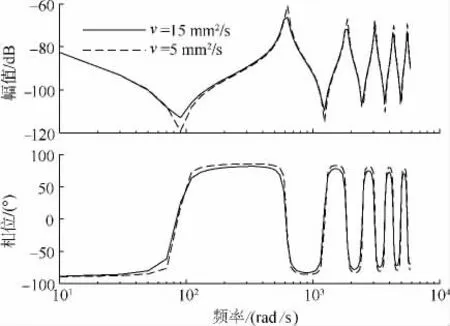
图8 不同油液黏度下Q v-P v传递函数伯德图

3.3 其他避免压力控制振荡的方法

实际应用中还经常采用增加阻尼比和降低开环增益的方法来避免压力控制振荡，包括在压力伺服阀中增加单向进油阻尼和降低供油压力等.在压力伺服阀中增加单向进油阻尼孔可以提高系统增压时的阻尼比，同时保持泄压的快速性.因此可以改善系统增压时的压力控制特性，但对于泄压的情况并没有改变.降低系统供油压力相当于降低了系统的开环增益，因此能较好地减少出现压力控制振荡的现象.但是这两种方法存在共同的缺点，即降低了压力闭环系统的响应速度，不利于飞机防滑控制性能的提升.

4 压力闭环控制仿真对比分析

本节通过时域仿真进一步分析了各个因素对飞机液压刹车系统压力闭环的影响.以表1中参数值为基准，仿真刹车系统中压力伺服阀对某压力指令的跟踪情况，结果见图9.由图9可知，在指令跟踪过程中，Pv振荡严重.

图9 压力伺服阀指令跟踪仿真结果

作为对比，将阀后管路长度增长至4m，其他参数、指令不变，仿真结果见图10.从图10可知阀出口压力Pv并没有出现严重振荡，与之前频域分析的结果相符，管路长度为4m避开了压力伺服阀的固有频率，提高了系统的稳定裕度，因此避免了振荡.

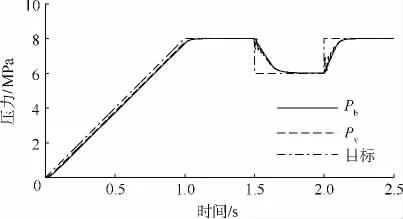
图10 管路长4m时压力伺服阀指令跟踪仿真结果

此外，保持管路长度为3m，假设油液弹性模量从1200MPa降低至700MPa，此时压力跟踪仿真结果如图11所示.Pv同样没有出现振荡，其原因正如图7所示，油液弹性模量的变化同样改变了管路容腔特性的谐振峰频率，避免了与阀特性的耦合.

图11 βe为700MPa时压力伺服阀指令跟踪仿真结果

最后仿真降低系统供油压力情况下系统的压力控制效果，如图12所示.由图12可知压力跟踪过程平稳，并没有出现明显振荡，但是系统对斜坡信号的跟踪变差，阶跃响应的调节时间也有一定增长.因此降低系统供油压力的方法牺牲了系统的指令跟踪性能.

图12 P s=12MPa时压力伺服阀指令跟踪仿真结果

5 结论

本文通过引入管路模型，分析了传统的基于压力伺服阀的飞机刹车系统存在的压力控制容易失稳的问题.通过分析发现，飞机液压刹车系统中，压力伺服阀阀后存在的长管路造成了阀出口压力的频率特性在某些频段上欠阻尼，从而使得压力伺服阀所构成的局部压力闭环容易出现稳定裕度不足的情况.而管路和油液的参数都影响着系统中管路容腔负载的频率特性.为了避免压力控制振荡、失稳的情况，可以通过匹配设计的方法，使管路容腔负载的谐振频率与压力伺服阀的固有频率尽量避开.同时，增加系统阻尼和降低增益的方法也能在一定程度上减少压力振荡，但是需要以牺牲系统性能为代价.

References)

［1］李树立，焦宗夏.液压流体脉动主动控制研究现状与展望［J］.机床与液压，2006:243 －246 Li Shuli，Jiao Zongxia.Research actuality and prospect of active control of hydraulic fluid fluctuation［J］.Machine Tool and Hydraulics，2006:243 －246(in Chinese)

［2］黄伟明，吴瑞祥，张燮年.神经网络及模糊控制在飞机防滑刹车系统中的应用［J］.航空学报，2001，22(4):317 －320 Huang Weiming，Wu Ruixiang，Zhang Xienian.Aircraft antiskid brake system with neural network and fuzzy control［J］.Acta Aeronoutica et Astronautica Sinica，2001，22(4):317 － 320(in Chinese)

［3］何恒，吴瑞祥，黄伟明.基于ANN与FNN的飞机防滑刹车系统设计［J］.航空学报，2005，26(1):116 －120 He Heng，Wu Ruixiang，Huang Weiming.Design of aircraft antiskid brake system with ANN and FNN［J］.Acta Aeronoutica et Astronautica Sinica，2005，26(1):116 －120(in Chinese)

［4］ Zhang Ming，Nie Hong，Wei Xiaohui，et al.Research on modelling and simulation for aircraft anti-skid braking［C］//2nd International Symposium on Systems and Control in Aerospace and Astronautics.Piscataway，NJ:IEEE Computer Society，2008:1－5

［5］ Wei Jianhua，Kong Xiaowu，Qiu Minxiu，et al.Transient response of a valve control hydraulic system withlong pipes［J］.Chinese Journal of Mechanical Engineering:English Edition，2004，17(1):31－35

［6］赵丙龙.考虑管道影响的阀控电液伺服系统建模仿真及应用研究［D］.太原:太原理工大学，2005 Zhao Binglong.The model building，simulation and application research of valve control electro-hydraulic servo system with pipe［D］.Taiyuan:Taiyuan University of Technology，2005(in Chinese)

［7］田源道.电液伺服阀技术［M］.北京:航空工业出版社，2008:36－53 Tian Yuandao.Technology of electro hydraulic servovalves［M］.Beijing:Aviation Industry Press，2008:36 －53(in Chinese)

［8］李运华.机电控制［M］.北京:北京航空航天大学出版社，2003:47－65 Li Yunhua.Mechatronic control［M］.Beijing:Beijing University of Aeronautics and Astronautics Press，2003:47 － 65(in Chinese)

［9］ Goodson R E，Leonard R G.A survey of modeling techniques for fluid line transients［J］.Journal of Basic Engineering，1972:94－474

［10］程鹏.自动控制原理［M］.北京:高等教育出版社，2010:201－215 Cheng Peng.Automatic control principle［M］.Beijing:Higher Education Press，2010:201 －215(in Chinese)