航空重载面齿轮三维裂纹分析与疲劳寿命预测
王延忠 田志敏 侯良威 兰 州
(北京航空航天大学 机械工程及自动化学院,北京 100191)
疲劳与断裂是引起工程结构和构件失效的最主要原因[1],应用于航空重载传动的面齿轮也不例外.在重载工况下工作的面齿轮其循环应力较大,有相当数量的塑性变形,在经历足够多次的载荷扰动作用之后,从高应力或高应变处开始,形成裂纹,此后在扰动载荷作用下,裂纹进一步扩展,直至到达临界尺寸而发生完全断裂.疲劳破坏一般要经历裂纹萌生、裂纹稳定扩展和裂纹失稳扩展(断裂)3个阶段,而裂纹失稳扩展是快速扩展,对寿命的影响很小,因此在估算寿命时只考虑裂纹萌生寿命和裂纹扩展寿命两部分:裂纹萌生寿命即产生规定长度初始可测裂纹的循环次数;裂纹扩展寿命为由初始可测裂纹扩展到临界长度的循环次数.
裂纹萌生寿命分析时,一般按应变-寿命关系进行;而裂纹扩展寿命分析则必须考虑裂纹的存在,需用线弹性断裂力学理论[2].
1 裂纹萌生寿命
应用应变-寿命关系进行裂纹萌生寿命分析,使用循环应力-应变模型和应变-寿命(ε-N)曲线,根据关键点的应变来预测裂纹萌生寿命.
1.1 循环应力-应变模型
材料的应力-应变迟滞回线如图1所示,其总应变由弹性应变和塑性应变两部分组成,即

式中,Δεt为总应变;Δεe为弹性应变;Δεp为塑性应变.
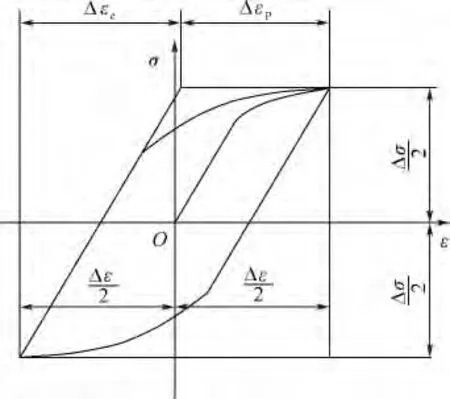
图1 应力-应变迟滞曲线
弹性应变Δεe和塑性应变Δεp可以分别写为

式中,Δσ为总应力;E为弹性模量;K'为循环强度系数;n'为循环应变硬化系数.
将材料疲劳强度系数σ'f和疲劳延性系数ε'f代替式(2)中的Δσ和Δεp可得

即

由式(1)~式(3)可得循环应力-应变曲线的表达式为
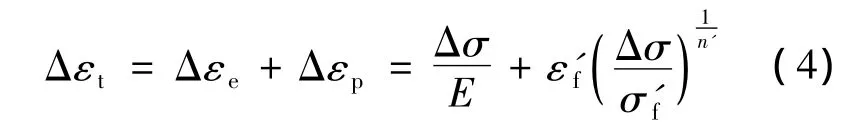
1.2 应变-寿命(ε-N)曲线
Basquin发现在对数坐标下,应力-寿命数据之间的关系是简单的直线关系,表示为

式中,2Nf是以反向数计的疲劳寿命,是以循环数计的疲劳寿命的2倍;b为疲劳强度指数.
则弹性应变可写为

Coffin和Manson发现塑性应变Δεp的对数与发生破坏的载荷反向次数2Nf的对数存在直线关系,即

式中c为疲劳延性指数.
总应变-寿命曲线(见图2)可用Basquin方程和Manson-Coffin方程的叠加来表示:

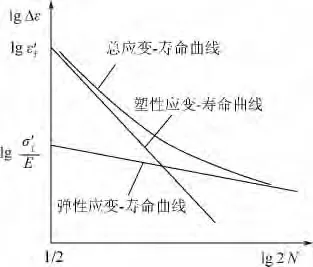
图2 总应变-寿命曲线
1.3 影响裂纹萌生寿命的因素
疲劳裂纹常萌生于试件表面,因此表面状况对其萌生寿命有显著影响.表面状况主要包括表面粗糙度、表面层的组织结构和表层应力状态,本文只分析表面粗糙度及氮化、喷丸工艺对裂纹萌生寿命的影响规律[3].
1.3.1 表面粗糙度
表面光洁度修正系数Csur与表面粗糙度Ra和材料抗拉强度Rm有关,其关系曲线如图3所示.

图3 表面光洁度修正系数C sur
而疲劳强度削弱系数Kf与表面光洁度修正系数Csur的转换关系式为

1.3.2 氮化、喷丸工艺
考虑氮化、喷丸工艺对裂纹萌生寿命的影响需进行表面敏感系数的修正.这些工艺改变表面层的组织结构或应力状态,使得疲劳强度得到提高,而表面敏感系数的确定依赖于试验[4].
2 裂纹扩展寿命
以线弹性破坏力学(LEFM,Linear-Elastic Fracture Mechanics)理论为基础,根据材料断裂韧性与疲劳裂纹扩展速率,预测有初始缺陷或裂纹面齿轮的裂纹扩展寿命.
2.1 裂纹扩展理论
按裂纹的力学特征,可以分为张开型裂纹(Ⅰ型裂纹)、滑开型裂纹(Ⅱ型裂纹)和撕开型裂纹(Ⅲ型裂纹).在一般受力情况下,裂纹通常属于复合型裂纹.
确定裂纹的开裂角和临界扩展条件,已有最大周向应力理论、最大能量释放率理论及应变能密度因子理论等脆性断裂理论.由于面齿轮产生的裂纹属于Ⅰ型+Ⅱ型+Ⅲ型复合型裂纹的扩展问题,因而采用应变能密度因子理论,其2个假设如下:
1)裂纹沿着应变能密度因子最小的方向开始扩展;
2)裂纹的扩展是由于最小应变能密度因子达到了材料的临界值Sc.
根据上述假设,建立起相应的断裂判据:
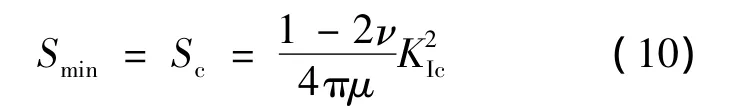
式中,ν为泊松比;μ为剪切弹性模量;KIc为Ⅰ型裂纹断裂韧度值.
2.2 裂纹扩展寿命计算
在研究高强度合金材料的疲劳裂纹扩展时,Paris应用线弹性断裂力学概念,将裂端应力强度因子和裂纹扩展速率联系起来[5],其关系在双对数坐标上是一条S形曲线,如图4所示.

图4 疲劳裂纹扩展lgd a/d N-lgΔK关系
第Ⅱ阶段d a/d N与ΔK在双对数坐标上呈线性关系,可用Paris公式表示为

式中,ΔK为应力强度因子范围,ΔK=Kmax-Kmin;C和m为材料常数,m为曲线的斜率.
将Paris公式积分,可得疲劳裂纹扩展寿命:
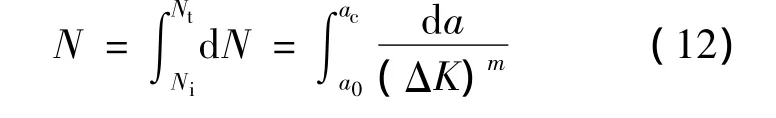
式中,a0为初始裂纹尺寸;ac为临界裂纹尺寸[6].
3 算例
根据以上理论,针对表1参数的齿轮进行寿命预测,包括裂纹萌生寿命和裂纹扩展寿命2部分.选用材料42CrMo4,E=2.1 ×105MPa,ν=0.3,且经热处理:810℃淬火 2min,油冷 3min,180℃回火2 h.

表1 齿轮参数
3.1 裂纹萌生寿命
利用MSC.Fatigue软件进行裂纹萌生分析,可以考虑表面粗糙度、表面处理工艺等因素对裂纹萌生寿命的影响.式(8)中,经查询所用材料42CrMo4对应的参数值分别为:n'=0.14,σ'f=1820 MPa,ε'f=0.65,b= - 0.08,c= - 0.76,σs=930MPa,σb=1080MPa.根据以上材料参数值添加材料属性,在材料库中建立42CrMo4模型,其应变-寿命曲线如图5所示.

图5 42CrMo4应变-寿命曲线
3.1.1 齿根最大弯曲应力计算
利用Abaqus进行面齿轮加载接触分析,定义2个分析步:第1个分析步圆柱齿轮绕自身轴线旋转微小角度使2齿面接触;第2个分析步在圆柱齿轮上施加旋转角速度1.74 rad/s,在面齿轮上分别施加 3000,4000,4 500,5 000,6 000N·m 的负载扭矩.通过模拟齿轮间的相互啮合过程,仿真得面齿轮齿根最大弯曲应力和齿面上的接触法向力.以负载扭矩5000N·m为例,其加载接触分析模型如图6所示.齿根最大弯曲应力为859.6MPa,该点的坐标为(-3.161 798,-122.359 635,-27.7794),齿面上的接触法向力为 35720.6N,其结果见图7.

图6 面齿轮加载接触分析模型

图7 面齿轮齿面接触法向力
3.1.2 裂纹萌生寿命预测
将Abaqus生成的fil结果文件导入MSC.Fatigue中,进行裂纹萌生的仿真计算.
面齿轮传动是圆柱齿轮和面齿轮间的点接触,发生齿面变形最终接触区为以接触点为中心的椭圆.为了方便仿真,考虑最危险情形,简化其载荷历程为作用于齿顶上一点的集中力,大小随时间的变化如图8所示.

图8 加载历程曲线
在Material Information菜单中,Finish选择默认的No Finish,Treatment选择默认的 No Treatment,KfValue 选择默认值 1.0.
从生成的寿命结果云图(图9)可以看出面齿轮齿根寿命最短的节点Node 6488即为面齿轮齿根最大弯曲应力的节点.
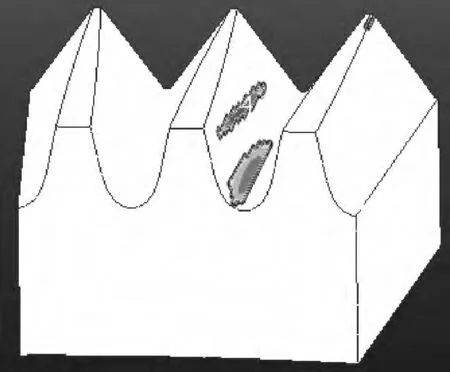
图9 Fatigue寿命结果云图
1)表面粗糙度影响.
上述结果未考虑齿面粗糙度,现分析Ra=0.8,1.6,3.2,6.3 μm 等粗糙度情况下的裂纹萌生循环次数,研究面齿轮齿面粗糙度对其裂纹萌生寿命的影响规律.由Csur曲线查得
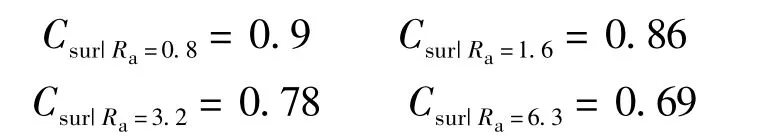
相应的
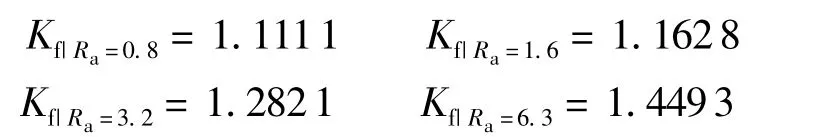
设置不同表面粗糙度对应的Kf数值,仿真得到相应情况下的裂纹萌生循环次数,其结果如图10所示.

图10 粗糙度对裂纹萌生寿命影响
从图10知,在相同载荷作用下随着粗糙度的减小,裂纹萌生循环次数在增大,可见提高齿面粗糙度有利于增加面齿轮裂纹萌生寿命.
2)表面处理影响.
对面齿轮齿面进行氮化和喷丸,分析其对裂纹萌生寿命的影响,部分结果为Beyond Cutoff,说明应力未达到材料的疲劳极限,由应变-寿命曲线知循环次数大于108.结果如图11所示.氮化处理后循环次数均超过108,喷丸处理应力约小于630MPa循环次数超过108,可见氮化最有利于裂纹萌生循环次数的增大,其次是喷丸.
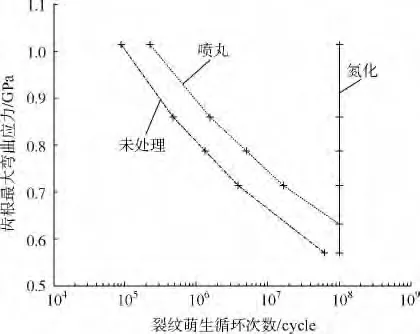
图11 表面处理工艺对裂纹萌生寿命影响
3.2 裂纹扩展寿命
3.2.1 裂纹扩展模型建立
3.2.2 应力强度因子计算
利用Franc3D进行裂纹扩展,其中第10和第20扩展步的扩展结果如图12所示.

图12 裂纹扩展过程中扩展步的扩展结果图
从裂纹扩展过程中应力强度因子的变化看出,随着裂纹的进一步扩展,Ⅱ和Ⅲ型应力强度因子与Ⅰ型相比可以忽略不计,因此可以用Ⅰ型应力强度因子作为判定裂纹断裂的依据[8].以5000N·m为例,其Ⅰ,Ⅱ,Ⅲ型应力强度因子的变化规律曲线如图13所示.

图13 Ⅰ,Ⅱ,Ⅲ型应力强度因子随裂纹扩展变化曲线
当负载不同时,应力强度因子变化历程曲线也不同,即拥有不同的裂纹扩展寿命.负载对应力强度因子变化历程的影响趋势如图14所示,负载越大,其裂纹扩展循环次数越少,断裂时裂纹扩展总长度越短.

图14 不同负载下的Ⅰ型应力强度因子随裂纹扩展变化曲线
3.2.3 裂纹扩展寿命预测
根据应力强度因子变化历程曲线求得不同负载下的裂纹扩展循环次数[9-10],见表 2.

表2 不同负载下的裂纹扩展寿命
3.3 疲劳寿命曲线
综合以上分析计算的裂纹萌生寿命和裂纹扩展寿命,考虑表面粗糙度和表面处理工艺,得到不同表面粗糙度和表面处理工艺下的齿根最大弯曲应力-总循环次数曲线,即疲劳寿命曲线,如图15所示.它可以用来指导实际生产活动中面齿轮的设计工作,预测面齿轮产品的使用寿命,避免产品失效导致的重大事故和经济损失.

图15 不同表面粗糙度、表面处理工艺下的疲劳寿命曲线
4 结论
本文应用应变-寿命关系和断裂力学理论,以MSC.Fatigue和Franc3D为工具,考虑面齿轮齿面粗糙度及氮化、喷丸表面处理工艺,分析计算在不同负载扭矩情况下的面齿轮齿根裂纹萌生寿命和裂纹扩展寿命,得到以下结论:
1)面齿轮齿面粗糙度的提高有利于增加其裂纹萌生寿命;
2)提高面齿轮齿根裂纹萌生寿命,表面处理工艺氮化优于喷丸;
3)面齿轮齿根裂纹属于复合型裂纹,但Ⅰ型应力强度因子占主导作用,可以作为断裂判据;
4)不同表面粗糙度、工艺下的疲劳寿命曲线为面齿轮的设计和使用寿命的预测奠定基础.
References)
[1]王军,邱志平.疲劳裂纹扩展的不确定理论[J].北京航空航天大学学报,2008,34(12):1428 -1432 Wang Jun,Qiu Zhiping.Uncertain theory for fatigue crack extension[J].Journal of Beijing University of Aeronautics and Astronautics,2008,34(12):1428 -1432(in Chinese)
[2]陈传尧.疲劳与断裂[M].武汉:华中科技大学出版社,2002:1-4 Chen Chuanyao.Fatigue and fracture[M].Wuhan:Huazhong University of Science and Technology Press,2002:1 -4(in Chinese)
[3]沈亮.齿轮疲劳寿命及齿根裂纹仿真分析[D].重庆:重庆大学,2011 Shen Liang.Simulation analysis of fatigue life and tooth root crack of gear[D].Chongqing:Chongqing University,2011(in Chinese)
[4]周传月,郑红霞,罗慧强,等.MSC.Fatigue疲劳分析应用与实例[M].北京:科学出版社,2005:5-36 Zhou Chuanyue,Zheng Hongxia,Luo Huiqiang,et al.Fatigue analysis and application of MSC.Fatigue[M].Beijing:Science Press,2005:5 -36(in Chinese)
[5]薛世峰,侯密山.工程断裂力学[M].东营:中国石油大学出版社,2012:50-102 Xue Shifeng,Hou Mishan.Fracture mechanics[M].Dongying:China University of Petroleum Press,2012:50 -102(in Chinese)
[6]李舜酩.机械疲劳与可靠性设计[M].北京:科学出版社,2006:11-140 Li Shunming.Mechanical fatigue and reliability design[M].Beijing:Science Press,2006:11 - 140(in Chinese)
[7] Glodez S,Sraml M,Kramberger J.A computational model for determination of service life of gears[J].International Journal of Fatigue,2002,24:1013 -1020
[8] 郭辉,赵宁,曹蕾蕾,等.渐开线直齿轮齿根裂纹扩展模拟[J].系统仿真学报,2007,19(13):2899 -2902 Guo Hui,Zhao Ning,Cao Leilei,et al.Crack propagation simulation for root of involute spur gears[J].Journal of System Simulation,2007,19(13):2899 -2902(in Chinese)
[9] Ural A,Heber G,Wawrzynek P A,et al.Three-dimensional,parallel,finite element simulation of fatigue crack growth in a spiral bevel pinion gear[J].Engineering Fracture Mechanics,2005,72:1148-1170
[10]于世光.渐开线齿轮齿根疲劳断裂特性分析[D].南京:南京航空航天大学,2009 Yu Shiguang.Analysis on tooth root fatigue crack properties of involute gear[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2009(in Chinese)

