非均匀螺距的双绞线串扰统计特性分析

包贵浩 苏东林 戴 飞

(北京航空航天大学 电子信息工程学院，北京 100191)

高万峰

(63863部队 八室，白城 137001)

随着传输线在电子电气系统的大量应用，在系统紧凑的内部空间中大量线缆通常被捆扎敷设，使得线缆间存在不同程度的串扰，严重的会使设备遭受干扰而导致性能降低或功能异常.在各类线缆中，双绞线凭借其良好的抗电磁干扰性在航空飞行器领域得到广泛的应用.它不仅可以通过相互绞合的方式来抵御外界电磁干扰，同时其一根导线在传输中辐射的电磁场会被另一根线上辐射的电磁场因反向而抵消，也可以降低自身信号的对外干扰.尽管如此，面对日益复杂的电子电气系统，双绞线在实际应用中依然会受到外界信号的干扰或对外干扰其他设备的正常工作.所以，开展双绞线串扰问题的研究具有重要的现实意义，有助于指导飞机电磁兼容性预设计［1］.

文献［2］最先提出双绞线的建模方法，将双绞线等效为不同平行线的级联，应用广义多端口网络的概念，分析双绞线的频域串扰.文献［3－4］提出的有限元(FEM，Finite Element Method)方法也是基于文献［2］的思想，不同之处在于后者采用FEM数值方法计算每组平行线的分布参数.双绞线实际上是双螺旋线，螺距可以定义为螺旋线上相邻对应点间的轴向距离.双绞线抗电磁干扰的机理是利用两条传输线的相互绞合，由此可见，其抗电磁干扰的能力是直接与螺距相关的，现有文献大多数是对均匀螺距的双绞线进行串扰分析，对非均匀螺距的分析较少.而在实际的电路和线缆中，非均匀螺距双绞线是不可避免的，如制作、布线和使用等都会造成双绞线螺距的非均匀性.文献［5］提出非均匀螺距对双绞线串扰预测的影响，但局限在假设螺距的误差为一特定值，缺乏随机性.螺距误差的随机性会造成双绞线串扰预测的不确定性.文献［6］是将螺距误差定义为服从均匀分布的随机变量，分析非均匀螺距双绞线的共模和差模干扰.

本文的特点是通过分析双绞线的制作原理，利用双绞线的制作参数求解螺距误差的概率密度函数，进而可更准确地分析任意双绞线串扰的统计特性.另外，对于非均匀螺距双绞线的建模，本文采用等弧度离散法，将任意双绞线以一定弧度离散后再应用多端口网络的概念进行级联.最后，仿真验证双绞线的制作参数对非均匀螺距双绞线串扰统计特性的影响程度.

1 螺距误差的概率分布

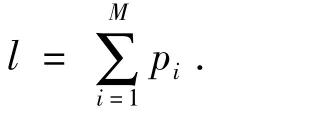
双绞线的制作原理可以用图2表示，其机械制作需要设置两个参数T1和T2，分别为转轴A和B的旋转周期.转轴A旋转1周，双绞线的长度l增加2πr1，双绞线长度 l的增长速度为 v=2πr1/T1.B旋转1周等于双绞线完成1次全扭.双绞线就是通过转轴A和B以固定周期T1和T2的旋转来实现的.

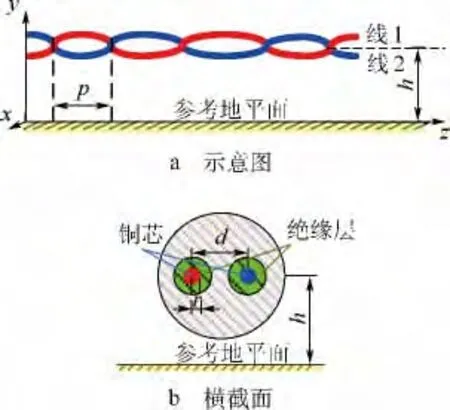
图1 非均匀螺距双绞线的示意图及其横截面

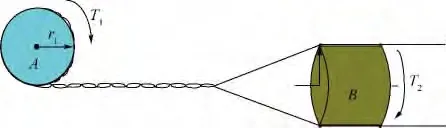
图2 双绞线的制作过程示意图

制作完成后，双绞线的径向长度l=2πr1·t/T1，其螺距的个数M=2t/T2，其中t为双绞线机械制作所需的时间，t为(1/2)·T2的整数倍.螺距的均值.螺距p可以用下式表示:

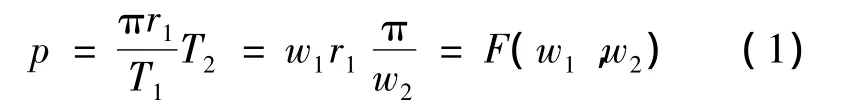
其中，r1为转轴A的半径;w1，w2分别为转轴A和B的角速度.

一般情况下，假设转轴A和B的角速度w1和w2分别服从和的正态分布，且两者相互独立.螺距误差Δ满足式(2):

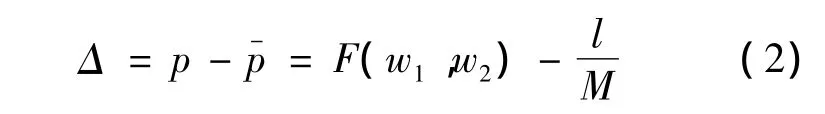
由此，可得螺距误差Δ的概率密度函数:

其中，fw1(w1)，fw2(w2)分别为角速度 w1，w2的概率密度.

2 非均匀螺距双绞线的串扰分析

2.1 非均匀螺距双绞线的离散化处理

对于任意双绞线，每段螺距pi存在不等的可能性，但其对应的旋转弧度均为π.本文对非均匀螺距双绞线采用等弧度离散法，以一定旋转弧度β=π/N对双绞线的各组螺距分别进行离散，将每组螺距分割成N段非连续的等长平行线，每段平行线的长度为

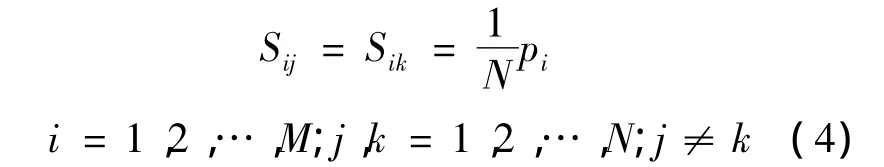
离散前后的双绞线模型如图3所示.

针对单线和双绞线间的串扰问题，在满足准静态和电小尺寸的条件下，忽略传输线损耗，可参照文献［7－9］给出的多导体传输线理论经验公式求解每段单线和两平行线间的分布参数矩阵Lij和Cij，从而建立第Sij段长度的集总参数π型等效电路，如图4所示.

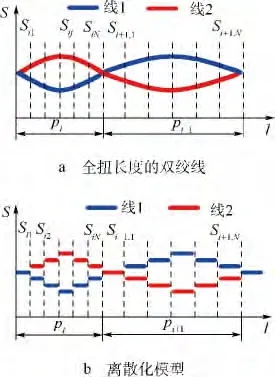
图3 全扭长度的非均匀螺距双绞线及其离散化模型

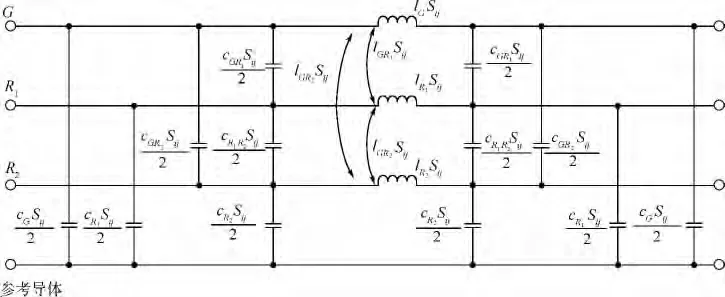
图4 第Sij段长度的集总参数π型等效电路

本文用多端口网络Tij来描述第Sij段长度的等效电路，再基于广义多端口网络的概念实现等效电路的级联.这样，每个螺距等效的多端口网络为Ti=Ti1Ti2…Tij…TiN，单线和双绞线等效的多端口网络为TTWP=T1…Ti…TM，如图5所示.

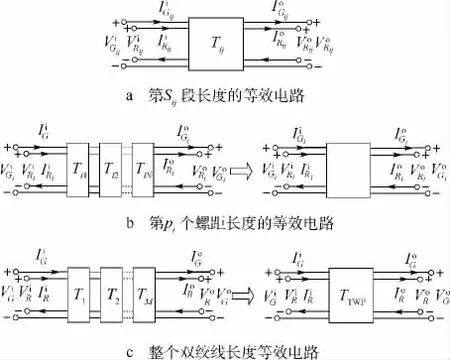
图5 不同长度下双绞线等效的多端口网络

2.2 非均匀螺距双绞线的频域串扰模型

双绞线串扰的分析是在给定传输线横截面尺寸以及终端参数 VS，RS，RL，RNE，RFE的条件下，预测双绞线近端和远端电压VNE和VFE，如图6所示.

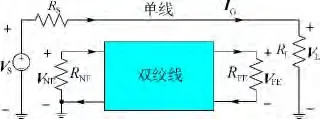
图6 单线和双绞线的串扰分析电路

作为受扰线，双绞线的感性和容性耦合模型如图7所示，其中Eij和Iij(j=1，2)分别为第i段螺距对应的感应电压源和感应电流源，公式如下:

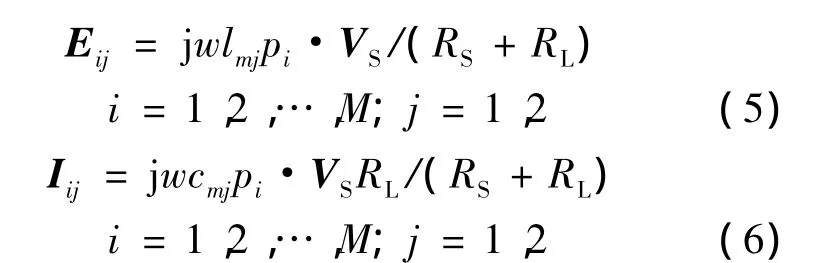
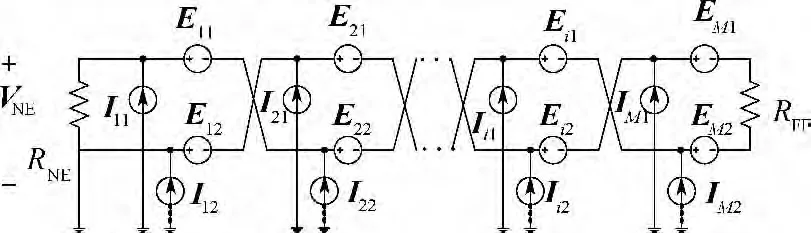
图7 双绞接收导线感性-容性耦合的简化模型

从感性和容性耦合的简化模型进而可以得到双绞线的近端串扰电压:

由式(7)可见，对于非均匀螺距双绞线，无论螺距个数M为奇数还是偶数，净感应电压源都不可能为一个定值.感性耦合会随着螺距的随机变化而发生改变，本文就是要分析感性耦合随螺距随机变化的统计特性.由于容性耦合与终端负载是否平衡有关，而不受扭绞的影响，故在此不做分析.

3 感性耦合的统计特性分析

双绞线的实际制作误差和随机布放会引入螺距误差Δ，感性耦合会随着螺距误差Δ的随机变化而改变，由式(5)和式(7)可以推导出感性耦合与螺距误差Δ的关系式:

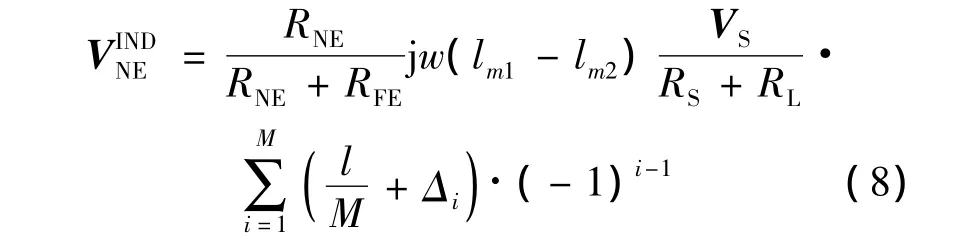
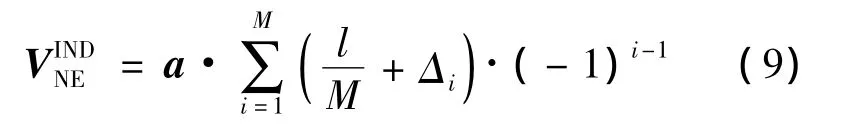
其中，当频率f一定时，a为确定的常数.

本文将螺距误差的 M维随机变量(Δ1，Δ2，…，Δi，…，ΔM)表示为M维行向量X，感性耦合写成矩阵形式为

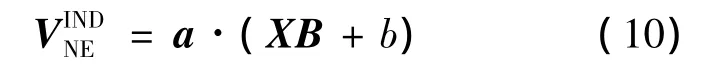
其中B为M维列向量［(－1)0，…，(－1)i，…，(－ 1)M－1］T;b=l(1 － (－ 1)M)/(2M).

由此可见，在求解完螺距误差Δ概率密度fΔ(Δ)后，利用式(9)或式(10)，就可以求得感性耦合的概率密度函数fV(V).

4 仿真验证

假定双绞线的制作参数转轴A和B的角速度 w1，w2分别服从和的正态分布.转轴A的半径r1=20 cm，制作时间t=(1/(2μw2))×n，n为正整数.仿真目的是不同参数设置条件下比较分析任意双绞线串扰的统计特性，具体仿真参数见表1.

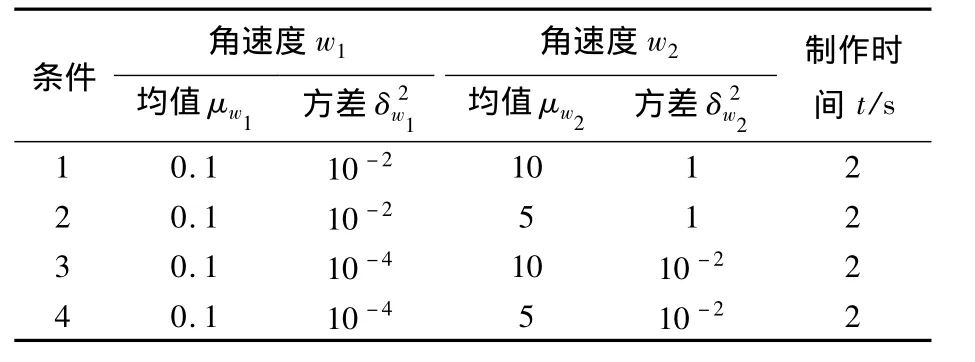
表1 不同仿真参数设置

假设单线为发射导线G，单束双绞线为接收导线R1和R2，单线一端接有电压源VS，终端电阻RS=RL=RNE=RFE=50Ω，如图6所示.单线与双绞线轴心的距离d=2 cm，两者距离地面的高度均为h=4 cm，单线和双绞线的铜芯半径均为r=0.5mm，屏蔽层半径均为 R=1.5mm，双绞线的线间距 ds=6mm，旋转弧度为 θ∈(0，2π)，具体如图8所示.在不同参数设置条件下，仿真近端感性耦合100次，频率范围为100Hz～1GHz.

图8 单线和双绞线的横截面示意图

仿真条件1和2的差别在于转轴B的角速度均值不同，导致双绞线螺距的长度和数目均不同.从图9可以看出，转轴B的角速度均值变小，任意双绞线串扰的概率密度函数曲线会向右偏移，产生非期望串扰的概率较高.

仿真条件1和3的不同之处是转轴A和B角速度的方差，条件3角速度的方差明显小于条件1.图10表示了任意双绞线串扰与转轴角速度方差的关系，角速度方差越大，产生非期望串扰的概率越高.

仿真条件1和4在角速度均值和方差上均不同.图11同样验证了角速度的均值和方差对任意双绞线串扰的影响.

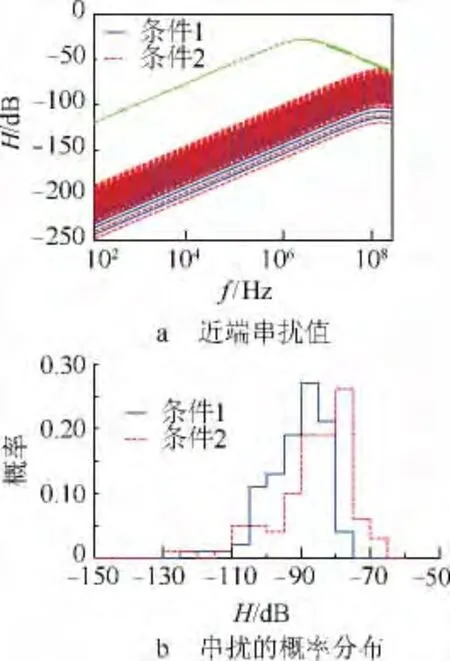
图9 条件1、条件2下的近端串扰值与在频率f=100MHz时近端串扰的概率分布

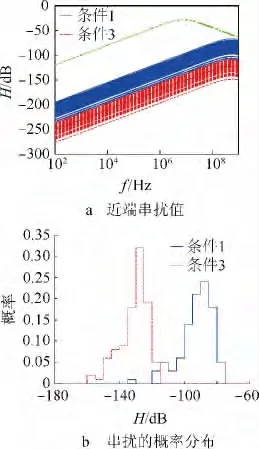
图10 条件1、条件3下的近端串扰值与在频率f=100MHz时近端串扰的概率分布

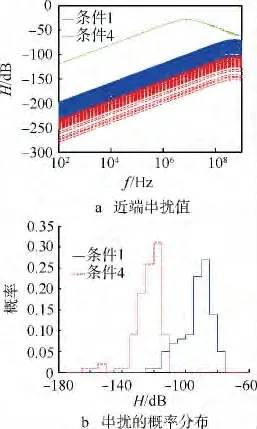
图11 条件1、条件4下的近端串扰值与在频率f=100MHz时近端串扰的概率分布

5 结论

双绞线的制作原理可以反映出螺距误差与制作参数转轴角速度间的关系，利用该制作参数可以较真实地得到螺距误差的概率密度函数.同时，采用等弧度离散的方法可以快速地建立非均匀螺距双绞线的频域串扰模型，基于该模型可推导出感性耦合和螺距误差的关系，进而可求得任意双绞线感性耦合的概率密度函数.最后，通过仿真分析，验证了转轴角速度的均值与方差是影响任意双绞线感性耦合的关键因素.因此，本文建议在双绞线制作过程中不可忽视转轴角速度的均值和方差，应尽量减小螺距误差，以保证双绞线一定的抗干扰能力.

References)

［1］苏东林，王冰切，金德琨，等.电子特种飞机电磁兼容预设计技术［J］.北京航空航天大学学报，2006，32(10):1241 －1245 Su Donglin，Wang Bingqie，Jin Dekun，et al.EMC pre-design technologies on EW special aircraft［J］.Journal of Beijing University of Aeronautics and Astronautics，2006，32(10):1241 －1245(in Chinese)

［2］ PaulC R，Mcknight J W.Prediction of crosstalk involving twisted pairs of wires［J］.IEEE Trans Electromagnetic Compatibility，1979，EMC-21(2):92 －114

［3］ Buccella C，FelizianiM，Manzi G，et al.Prediction of voltage and current propagation in twisted wire pairs(TWPs)by a circuit model［C］//IEEE International Symposium on Electromagnetic Compatibility.Piscataway，NJ:IEEE，2005，1:51 －55

［4］ Buccella C，Feliziani M，Manzi G.Three-dimensional FEM approach to model twisted wire pair cables［J］.IEEE Transactions on Magnetics，2007，43(4):1373 －1376

［5］ Spadacini G，Bellan D，Pignari SA.Impact of twist non-uniformity on crosstalk in twisted-wire［C］//IEEE International Symposium on Electromagnetic Compatibility.Piscataway，NJ:IEEE，2003，2:483 －488

［6］ Pignari SA，Spadacini G.Influence of twist-pitch random non-uniformity on the radiated immunity of twisted-wire pairs［C］//2011 30th URSI General Assembly and Scientific Symposium，URSIGASS 2011.Piscataway，NJ:IEEE，2011:1 －4

［7］ Paul C R.电磁兼容导论［M］.2版.闻映红，译.北京:人民邮电出版社，2007:372－379，444－445 Paul C R.Introduction to electromagnetic compatibility［M］.2nd ed.Translated by Wen Yinghong.Beijing:Posts ＆ Telecom Press，2007:372 －379，444 －445(in Chinese)

［8］ Paul C R.Analysis of multiconductor transmission lines［M］.2nd ed.New York:Wiley-Interscience，2007:40 －81

［9］ Paul C R.Solution of the transmission line equations under the weak coupling assumption［J］.IEEE Trans Electromagnetic Compatibility，2002，EMC-44(3):413 －423