核电磁脉冲作用下不均匀双绞线的时域耦合特性分析∗

廖慧敏 刘其凤 吴为军

（中国舰船研究设计中心电磁兼容性重点实验室 武汉 430064）

1 引言

随着集成技术的快速发展，采用了大量低电压集成芯片、电路的电子设备越发敏感，外界电磁脉冲环境影响敏感电子设备的途径可分为前门耦合和后门耦合，其中，后门耦合是指外界电磁脉冲通过电子设备暴露在外的金属外壳或是线缆耦合到设备内部。兼具良好抗干扰性能和价格低廉等特性的双绞线，一直在各类系统中担负着控制信号、电源信号的传输，在航空、航天、航海等领域都获得了广泛应用。早在1970年代，国内外的学者就开始了对传输线的场线耦合特性的研究［1～4］。分析外界电磁场与传输线的耦合，其方法主要分为全波分析法和高频近似法，计算机技术的发展让这些方法都能得到很好的发展。全波分析法有有限差分法、有限积分法、有限元法、传输线法、矩量法等，场线耦合计算模型，是基于传输线理论提出的，根据将场线耦合作用等效为的激励源的定义不同，可分为Agrawal、Taylor、Rachidi三类［5～6］。

针对双绞线，分析方法为将其等效为多段级联的平行双线，再根据实际情形采用全波分析法或高频近似法进行求解。Akiyoshi Tatematsu采用时域有限差分方法结合Agrawal模型，来计算双绞线的场线耦合时域特性［7］。Yan Y等采用时域有限差分法来研究双绞线在外场照射下的瞬时终端响应［8］。国内外的学者还做了许多实验研究。陈亚洲等人进行了辐照实验，来研究双绞线网络在雷电电磁脉冲辐照下的耦合特性［9］。

针对双绞线，大多数的研究都是基于一个基本假设，其几何结构服从均匀的双螺旋结构，然而，由于制作工艺、安装环境等因素限制，实际工作中的双绞线结构并非严格服从双螺旋结构。双绞线的不均匀具体体现在，双绞线的每个扭距不一定相等，且整段双绞线的扭距个数不一定是整数个。国内外的学者对均匀双绞线的研究较多，对不均匀扭曲双绞线的研究较少。

研究针对不均匀扭曲双绞线展开，引入表征双绞线不均匀度的因子，建立双绞线时域场线耦合模型，利用链参数和多端口级联的方法来分析不均匀双绞线的时域耦合特性，提供一种更加准确的预测结果。

2 双绞线时域场线耦合模型

2.1 双绞线结构模型

理想双绞线的几何结构服从双螺旋结构，其结构示意图如图1，双绞线沿Z轴走向，s为双绞线两线之间的间隔，L为双绞线沿Z轴的长度，扭距用p表示，扭距均匀的双绞线，其扭距p为一个固定的常数，不均匀双绞线的扭距p是在一定范围内的随机数。其两线上的点的坐标位置可如下表示［10］：

图1 双绞线结构示意图

其中，xm，ym，zm是两条线上的点在直角坐标系三个方向上的坐标，m代表线的编号，其取值为（1，2），x0和 y0表示双绞线两线的中心位置。

研究针对无损耗的双绞线，单位长度电感矩阵，单位长度电容矩阵的具体计算公式皆见于文献［10］，其矩阵中的具体元素定义如下，见图3。其中，μ为磁导率，h为离地高度，r为线半径，s为两线间距，i，j为线的编号，取值为（1，2）。

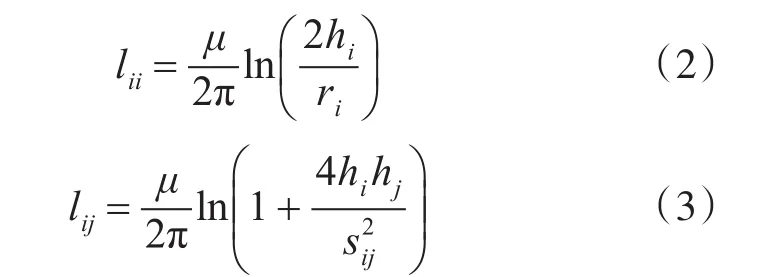
2.2 双绞线场线耦合方程

假设双绞线位于远场区域，外界电磁脉冲可被视为平面波场，入射场的定义如下［10］：

其中，ex，ey，ez分别为场矢量在直角坐标系上x，y，z方向上的分量，kx，ky，kz为各方向上的相位常数分量，ω是角频率。

外部场耦合到线缆的过程，可以看作是外部场在线缆上感应出电流和电荷，这些电流电荷将会进一步产生散射场，这散射场与外部场一起组成了整个电磁环境，且满足边界条件。传输线方程可由单位长度等效电路所推导得出，针对长为L的传输线，在传输线两端的解有如下形式［11］：

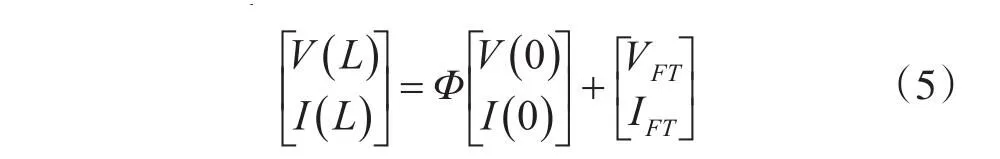
Φ代表传输线的链参数矩阵，VFT，IFT为入射场辐射等效的电压源和电流源表示两端的电压电流值。

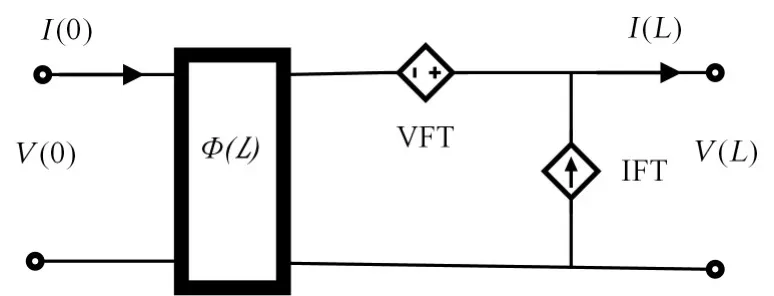
图2 外部场激励下的传输线等效图

由此解形式可得，入射场激励下的场线耦合效应可由一段无激励的传输线和等效激励源联合表示，如图2。传输线方程的解只给出了传输线两端电压和电流的对应关系，还需结合终端条件才能求得线上的电压电流。

终端条件采用戴维南等效，YS，YL为终端的导纳矩阵：

将终端条件代入，可得最终解为

为求解时域响应，将所得电流作反傅里叶变换：

其中，ω0为角频率间隔。

3 模型验证及计算结果

将双绞线的每节扭距等分成N等份，每一小段的长度为p/N，先分别求解每小段传输线相对应的链参数矩阵和等效源，再利用多端口网络级联的概念，求出整段双绞线的链参数矩阵以及等效源，结合终端条件，最终求得线上的电压电流值，以此求得感应功率，并对电流进行反傅里叶变换，得出时域响应。

3.1 模型验证

为验证模型的准确性，将模型应用于计算均匀扭距双绞线的在均匀平面波作用下的感应功率，并与文献［12］中的实验测量数据相比较，见图3。双绞线参数为：线半径0.25mm，双绞线两线的线间距为1.28mm，导线上覆盖绝缘层，外径为0.64mm，其相对介电常数为1.32，扭距为0.11m，总长0.44m，两端分别连接50Ω的负载。

模型计算结果与实验测量结果呈现良好的吻合性，虽然有一定的偏差，但是可能是测量工具、测量方法造成的，模型的有效性得到了肯定的验证。

图3 模型计算结果与实验测量结果对比图

3.2 双绞线总长度对耦合特性的影响

接下来研究核电磁脉冲辐射下，双绞线的场线耦合特性。核电磁脉冲采用贝尔实验室发布的标准，其上升时间4.1ns，下降时间550ns，采用双指数函数表达，其频域表达式如下：

图4 核电磁脉冲

其中，a=4*106，b=4.76*108。

其时域波形图和频域波形图见图4。

在此次仿真中，双绞线的参数设置如下：线半径0.25mm，双绞线两线的线间距为1.28mm，导线上覆盖绝缘层，外径为0.64mm，其相对介电常数为1.32，端接50Ω的负载。

首先，选取扭距值为0.1m的双绞线，其总长度分别选取为1m、2m、4m、8m。计算结果如图5。可见，在扭距值不变总长度增加的情况下，能量峰值点连成的包络面不变，随总长度的增加，谐振点数量变多。总长为1m、2m、4m、8m的双绞线分别在261.1MHz、130.6MHz、65.3MHz、32.6MHz频点的整数倍处，其耦合能量有谷值；其耦合能量的峰值分别在 130.6MHz、65.3MHz、32.6MHz、16.3MHz频点的奇数倍处。总长为1m、2m、4m、8m的双绞线耦合能量的均值分别为-190.02 dBm、-190.12 dBm、-190.42 dBm、-190.3dBm。

图5 双绞线长度对耦合特性

图6 双绞线扭距对耦合特性

从时域来看，总长为1m、2m、4m、8m的双绞线的感应电流的最大幅值分别为2.9mA、2.84mA、2.88mA、2.88mA。可见，在此频段内，暴露在外的双绞线长度的增加不会导致耦和能量的增加。

3.3 双绞线扭距长度对耦合特性的影响

接下来，观察在总长度不变的情况下，双绞线扭距尺寸变化对场线耦合特性的影响规律。

表1 扭距p不同取值对应的功率特征

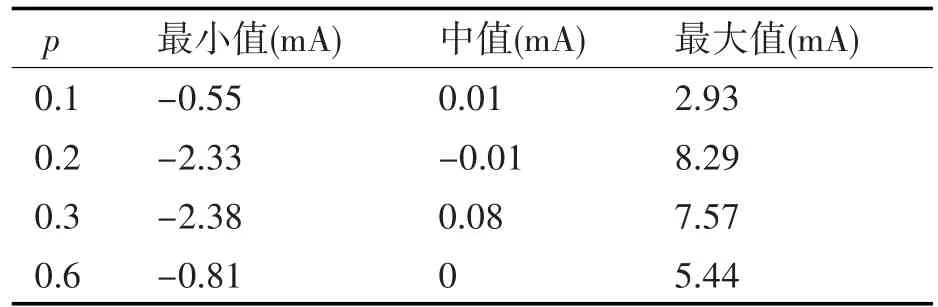
表2 扭距p不同取值对应的感应电流特征

选取扭距值分别为0.1m、0.2m、0.3m、0.6m，总长度为3m。计算结果如图6，对应的特征值见表1、表2。从频域来看，对于此结构此长度的双绞线，在400MHz以内，随着扭距的增加，耦合能量有一定的增加，从耦合能量平均值来看，扭距分别为0.1m、0.2m、0.3m、0.6m的总长3m的双绞线的耦合能量平均值分别为-190.30dBm、-181.72dBm、-172.23dBm、-169.23dBm，并且，扭距为0.6m的双绞线在频点435.4MHz处有耦合能量的最大值，扭距为0.3m的双绞线在频点870MHz处有耦合能量的最大值。从时域来看，扭距值分别为0.1m、0.2m、0.3m、0.6m的总长3m的双绞线的感应电流的最大幅值分别为2.93mA、8.29mA、7.57mA、5.44mA。

3.4 不均匀（扭距服从正态分布）双绞线的场线耦合特性

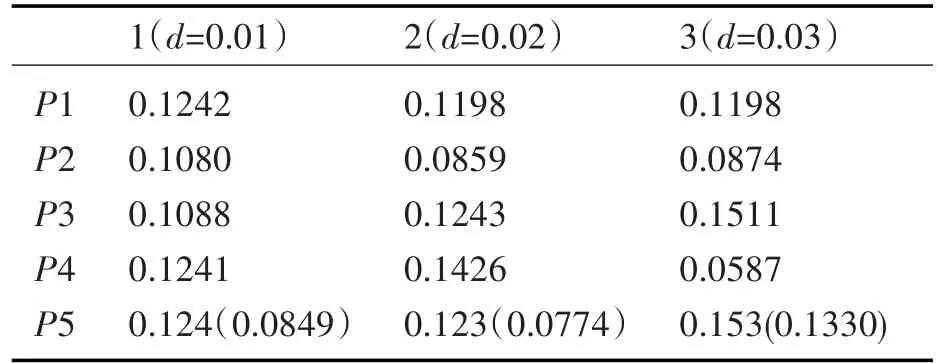
表3 扭距正态分布的三组双绞线每个扭距的取值

选取总长为0.55m的双绞线，在此，假设扭距服从正态分布P～N（P0，d），其均值为P0，d为方差，表征其不均匀程度，d越大，双绞线的扭曲则越发不均匀。均值P0为0.11m，d分别取0.01，0.02，0.03。三组双绞线每个扭距的取值如表3。

为保证双绞线的总长度不变，需对第五节扭距进行稍微调整，上表中括号内的值即为调整过后的扭距取值。调整过后的三组双绞线的每个扭距取值见图7。

图7 扭距正态分布的三组双绞线扭距直方图

图8 均匀双绞线与不均匀双绞线（扭距服从正态分布）的频域波形对比图

模型求解结果见图8，可得出结论，相对于俊均匀扭距的双绞线，不均匀扭距双绞线的谐振点数量增加。不均匀度d为0、0.01、0.02、0.03分别对应着耦合能量均值为-186.1dBm、-184.9dBm、-185.8dBm、-182.7dBm。表4为d不同取值时，感应功率的数值特征。通过反傅里叶变换，得到线上感应电流的时域图形，见图9。

表4 d不同取值时相对应的感应功率值特征

表5 d不同取值时相对应的感应电流值特征

表5为d不同取值时，感应电流值的数值特征，可见，当双绞线不均匀扭曲时，感应电流的峰值有起伏变化。

图9 均匀双绞线分别与不均匀度d=0.002、d=0.004、d=0.006双绞线的时域波形对比图

进一步研究，假设扭距服从均匀分布P～U（a0，b0），选取总长为0.55m的双绞线，P在此长度区间的任意一点取值概率相等，此长度区间的中心点为a，b为a到区间边缘的距离，b越大，P的取值范围就越大，双绞线的扭曲则越发不均匀。中心点a为0.11m，b分别取0.01，0.02，0.03。

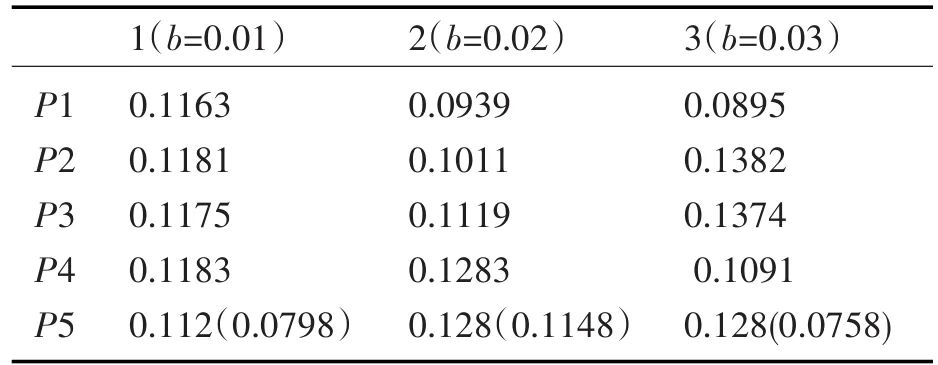
表6 扭距均匀分布的三组双绞线每个扭距的取值

三组双绞线每个扭距的取值如表6。同样，需对第五节扭距进行稍微调整以保证双绞线的总长度不变，上表中括号内的值即为调整过后的扭距取值。调整过后的三组双绞线的每个扭距取值见图10。

图10 扭距均匀分布的三组双绞线扭距直方图

模型求解结果见图11，可得出结论，当扭距不均匀时，双绞线的谐振点相对于均匀扭曲时数量有所增加，b为0、0.01、0.02、0.03分别对应着耦合能量均值-186.09dBm、-184.44dBm、-184.93dBm、-181.47dBm。表7为b不同取值时，感应功率的数值特征。

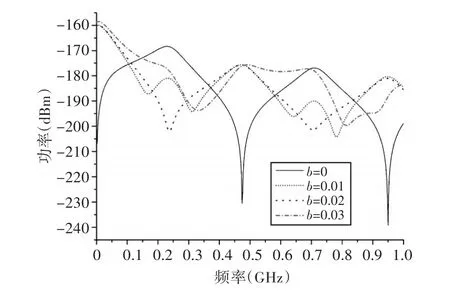
图11 均匀双绞线与不均匀双绞线（扭距服从均匀分布）的频域响应对比图的频域波形对比图

表7 b不同取值时相对应的感应功率值特征

通过反傅里叶变换，得到线上感应电流的时域图形，见图12。表8为b不同取值时，感应电流的数值特征，可见，当双绞线不均匀扭曲时，感应电流的峰值会发生变化。

图12 均匀双绞线分别与不均匀度b=0.01、b=0.02、b=0.03双绞线的时域波形对比图

表8 b不同取值时相对应的感应电流值特征

4 结语

本文针对不均匀双绞线的场线耦合特征进行研究，计算在核电磁脉冲作用下的双绞线的频域特性和时域特性，所建立的模型针对实际工程中的双绞线更具有现实意义，对场线耦合效应的预测更加准确。在所研究的频段内，暴露在外的双绞线长度的增加不会导致耦和能量的增加；对于此结构此长度的双绞线，在400MHz以内，随着扭距的增加，耦合能量有一定的增加。

无论双绞线的扭距服从正态分布还是均匀分布，都可以得出以下结论，在频域来看，不均匀双绞线同理想的双绞线相比，其谐振点增多。

扭距为0.11m的双绞线，总长5个扭距共0.55m，若是均匀双绞线，则其谐振点应该在237MHz的整数倍频点处，但扭距的不均匀会导致谐振点的增加，可以看做：不均匀双绞线的响应是由五对均匀双绞线的响应叠加而成，这五对双绞线的扭距分别对应不均匀双绞线的5个不同扭距，故这是五对扭距有细微差别（从而导致总长度也要细微差别）的双绞线，从而为造成耦合能量均值有扰动，且谐振点增多的现象。对时域而言，不均匀程度对感应电流的峰值会有所影响，所以尽量减少双绞线的不均匀度将有利于易被电流烧毁的器件的正常工作。