基于解析法的弹性板-柱壳结构外场声辐射有源力控制

李鸿秋,陈国平,谢琳艳

(1.金陵科技学院机电学院,江苏 南京 211169; 2.南京航空航天大学航空宇航学院,江苏 南京 210016)

弹性薄板-壳-声腔封闭结构在工程实际中应用极广。对弹性矩形板、圆板或者圆柱壳的振动产生的声辐射研究由来已久,而且也已经相对成熟[1]。近年来,研究方向倾向于多个弹性板或者弹性板(壳)通过耦合连接之后产生的声辐射,Dowell等[2]建立了弹性薄板-声腔结构的耦合理论模型,这类结构多用于飞机、汽车等乘坐舱。Kim等[3]发展了Dowell的理论,但是缺点都是需要求解圆板和圆柱壳的振动微分方程,而此类方程的求解较为复杂,因此已有解法大多采用Rayleigh-Ritz等数值方法或半解析方法[4]。对结构-声耦合问题的研究也大多集中在耦合系统的建模以及定性分析上。结构-声腔具有怎样的耦合特性以及结构-声腔耦合后外声场的声压级解析解还少有报道。弹性板(壳)-声腔系统的振动与耦合特性研究的难点在于边界条件的假设与简化,已有方法一般只限于简支边界。因此关于弹性圆板、圆柱壳结构与声腔耦合特性的研究必然具有重要的理论意义和实用价值。

本文设定板壳边界条件,并考虑内部声腔的影响,分别求解弹性圆板和圆柱壳的位移响应,建立弹性板-壳-声腔耦合结构的分析模型。并分别推导考虑声腔耦合作用的影响下弹性板以及圆柱壳受到外载荷时振动产生声辐射在外场指定点的声压级公式;推导外载荷单独作用在弹性板上以及弹性圆柱壳上时,弹性板以及弹性圆柱壳振动产生的声辐射在外场指定点的声压级表达式。进而根据外场点声压级的表达式探讨有源力噪声控制,并给出算例。

1 弹性板-壳-腔体结构声振耦合分析

2.1 弹性板-圆柱壳-声腔结构耦合频率的求解

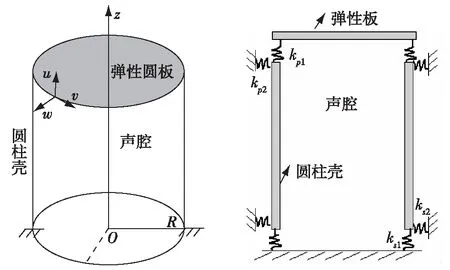
图1 弹性板-壳-声腔耦合结构及系统示意Fig.1 The plate-shell-cavity system

车辆的驾驶室,石油工业中的储油罐,航天飞机的舱室等都可以看做薄壁圆柱结构和平板结构的相结合的复杂结构,本文建立一端固定,一端用弹性圆板封闭的圆柱壳(弹性板-壳-声腔系统)耦合结构动力学模型,探讨此类结构的声振耦合特性以及噪声控制。弹性板的振动分为弯曲振动和面内振动,弯曲振动位移方向与板结构的中性面垂直,面内振动则存在于板结构所在的平面。杜敬涛、Gorman和Li[5-6]分别建立了矩形板在不同边界条件下的振动模型。

图1为弹性板-壳-声腔耦合结构及系统示意图,圆柱壳轴向,周向和径向3个方向的运动分别用u,v,w表示。边界条件通过设置不同的刚度kp1,kp2,ks1,ks2表示。假设弹性刚度ks1,ks2沿弹性板和弹性柱壳连续分布。

极坐标下,完整圆板的振型解为:

Wnp(r,θ)=[AnJn(αr)+BnIn(αr)]cos(nθ)

(1)

An,Bn为待定系数,可以通过边界条件确定。声压作用下弹性圆板的位移响应可以表示为:

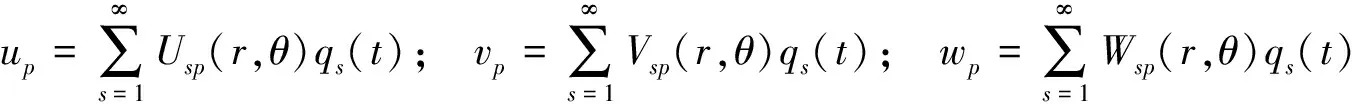
(2)

Usp(r,θ)、Vsp(r,θ)、Wsp(r,θ)分别表示第s阶弹性圆板的固有振型函数。

声压作用下,弹性圆柱壳的位移表示为:

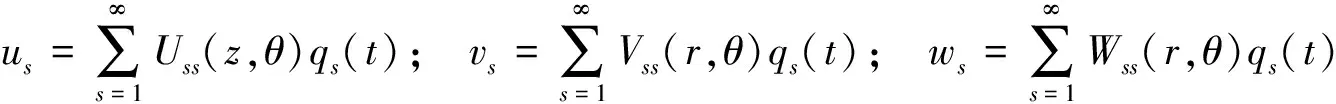
(3)

其中,Uss(z,θ)、Vss(z,θ)、Wss(z,θ)分别表示第s阶弹性圆柱壳的固有振型函数。

将up、vp、wp、us、vs、ws分别代入弹性圆板和圆柱壳的振动微分方程,并考虑到振型Wsp、Wss已经分别满足圆板和圆柱壳的振型方程组,因此可得:

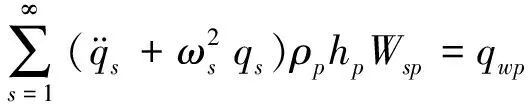
(4)

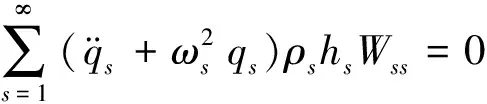
(5)

将式(4)两端同时乘以Wkp,然后在圆板中面上积分,将式(5)两端同时乘以Wks,然后在圆柱壳中曲面上积分,同时考虑振型的正交性特点得:

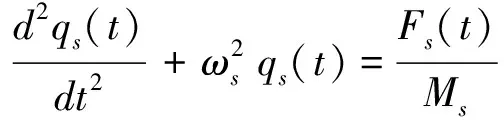
(6)

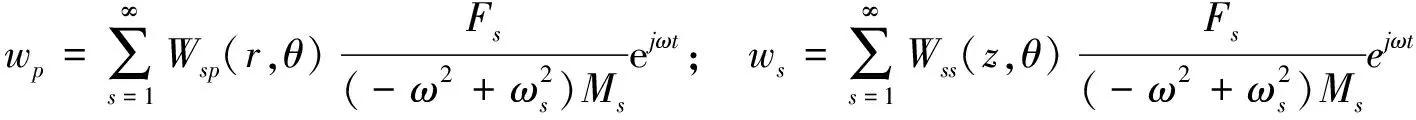
(7)

且:

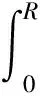
(8)

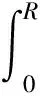
(9)

三维声波方程中取cos(nθ)项进行分析,将圆柱壳中声腔内声场的声压可以表示为:

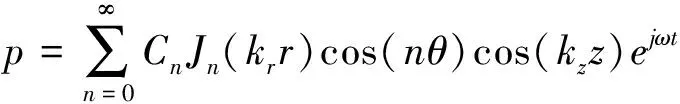
(10)

由弹性圆板和柱壳交界面处速度协调性条件以及腔内声压值,并利用贝塞尔函数性质,对于不同的n得到关于An,Bn,Cn,kr,kz,ω的6个方程,应用拟牛顿迭代方法求解此方程组,令n=1,得到第1阶耦合频率,同样,令n=2,可得到第2阶耦合频率,再计算n=3,4,…N。

2.2 考虑声振耦合求板-壳-腔结构中板和壳的位移响应

考虑内腔声压的作用,忽略外场声压对结构的作用,内腔声压垂直作用在弹性板和弹性壳的内表面,弹性板(壳)-声腔形成结构-声场的耦合结构。同上节的计算方法,弹性圆板弯曲位移和弹性柱壳的径向位移可以表示为:

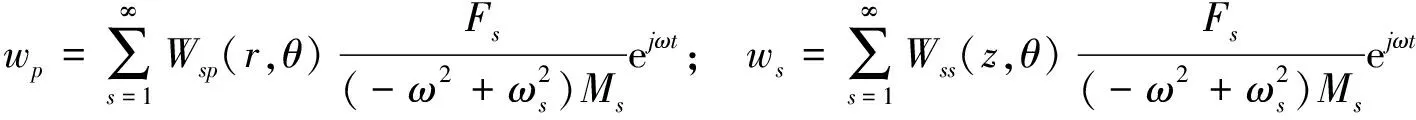
(11)

其中,ω为结构和声腔耦合后声腔的频率,ωs表示结构和声腔耦合后弹性板(壳)结构的频率。Wsp(r,θ)表示第s阶圆板弯曲振型函数、Wss(z,θ)表示圆柱壳径向振型函数。

2.3 弹性板-壳-声腔耦合系统的外辐射声场

弹性板-圆柱壳-声腔结构如图2所示,根据板-壳-腔的耦合模型分别推导外力单独作用在弹性板或者作用在圆柱壳上在外场点引起的声辐射声压级表达式。根据声辐射的叠加性原理,计算外力作用在弹性板或者作用在弹性壳上,板壳振动产生的声辐射在外场点的声压值之和。

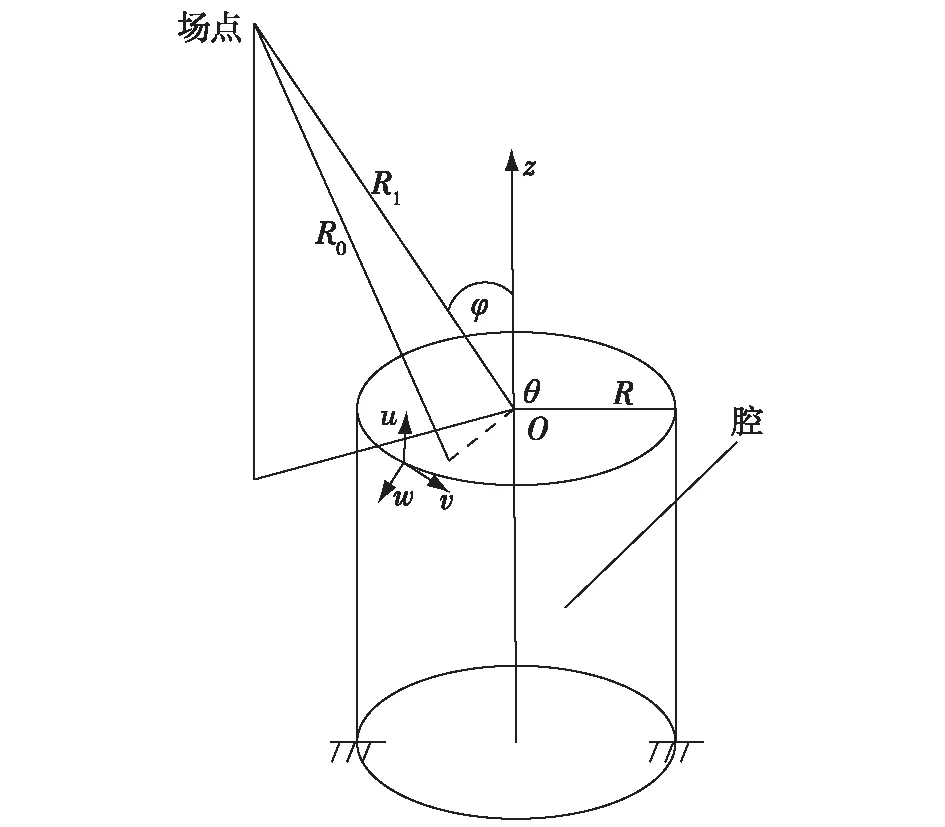
图2 外场点以及弹性板-声腔耦合结构示意Fig.2 The exterior point and the plate-shell-cavity system

2.3.1 考虑内腔声的影响弹性板振动产生的声辐射在外场点的声压值 弹性体-声腔结构振动引起的外场点声压值为:

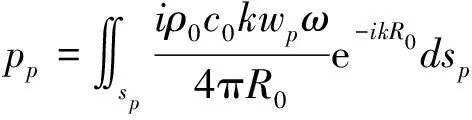
(12)

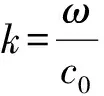
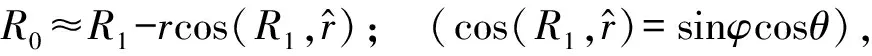
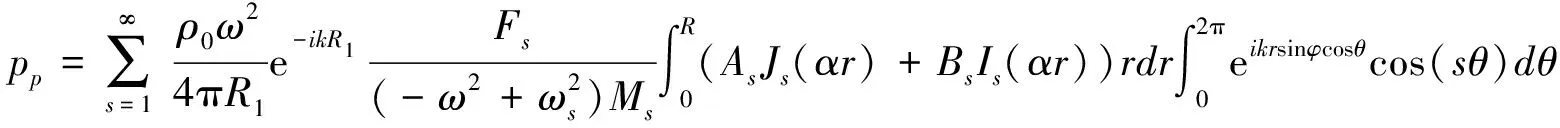
(14)

根据贝塞尔函数性质:

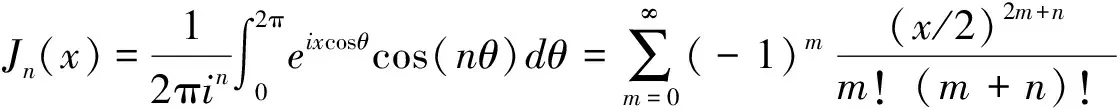
(15)

因此,式(14)可以写成:

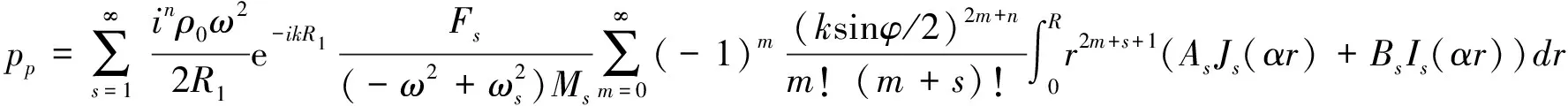
(16)

2.3.2 考虑内腔声的影响弹性壳振动产生的声辐射在外场点的声压值 外场点位于远声场时,弹性体-声腔耦合后,圆柱壳的外辐射声场声压值可以写成[7]:

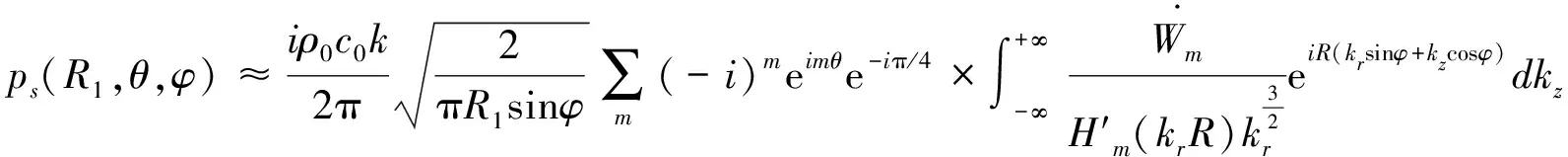
(17)

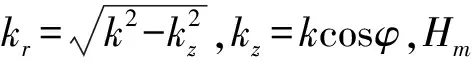
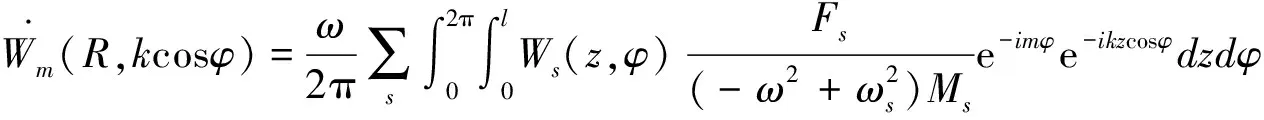
(18)

将式(18)代入式(17),利用稳相法得:

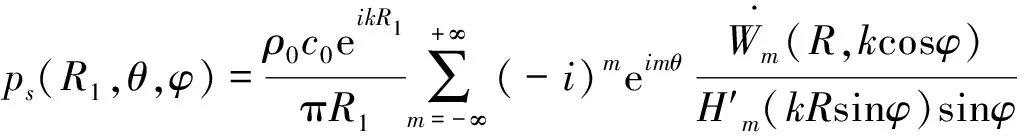
(19)

因此,弹性板(壳)-声腔耦合结构的声辐射外场指定点声压值可以表示为:

p(R1,θ,φ)=pp(R1,θ,φ)+ps(R1,θ,φ)

(20)

3 次级力源减振降噪分析

在结构的振动中有针对性的控制影响较大的一阶或几阶模态,只要设法使模态力Fs=0,则可以完全控制第s阶模态,而且仅需一个次级力源Fs1ejωt,由前文知,当受力点位于弹性板上,则在外场点指定位置的声压值为:

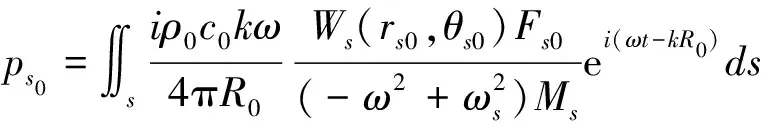
(21)

初级力的模态力为Fs0,由于次级力源Fs1的作用,在指定点位置处的产生的声压为:p=ps0+ps1,如果初始力为单点激励,要使p=0,且定义次级力源与初级力源的振幅比为:

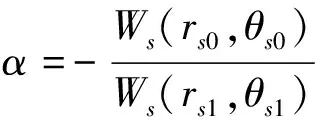
(22)

控制多阶模态振动,则需要采取多个次级力源,需要满足:

Fi=0; (i=1,2,..n)

(23)

即:

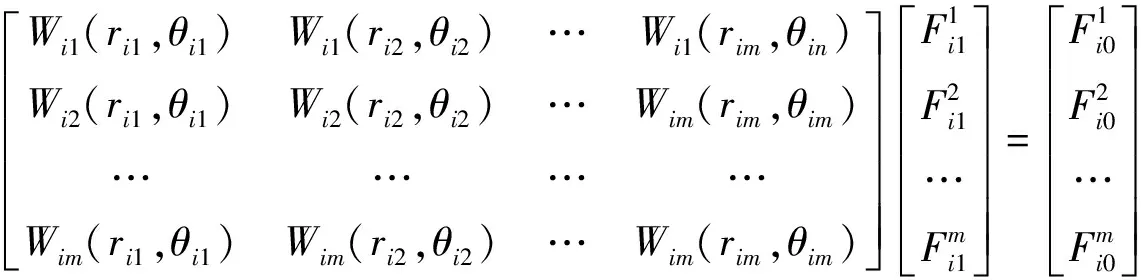
(24)

通常情况下,上式有唯一解。

4 算 例

算例结构如图2所示,圆板的几何尺寸及材料常数为:半径R=0.5 m,厚度h=0.001 m,弹性模量Ep=2.1e11 N/m2,密度ρ=7 850 kg/m3,泊松比ν=0.3,声波的传播速度c=340 m/s,空气的密度ρ0=1.21 kg/m3,声腔的深度l=1 m。设外载荷作用在弹性圆板上,激励点位置为弹性圆板上的(0.12 m,π/4) 处,激励力为单位简谐力,取需要控制的外场点位于(3 m,π/4,4 m) 处。针对第1阶模态振动予以控制,次级力源的位置不能位于模态节线处,因此,本文取次级力源的位置分别为(0.02 m,5π/4)、(0.02 m,3π/4)处。根据式(1)和式(22)求解得到次级力源与初级力源的振幅比见表1,表2。

表1次级力源的位于(0.02m,5π/4)对应不同模态振动控制次级力源与初级力源的振幅比

Table1Theamplituderatiobetweentheprimaryforceandthesecondaryforcewhenthesecondaryforceisexertedat(0.02m,5π/4)

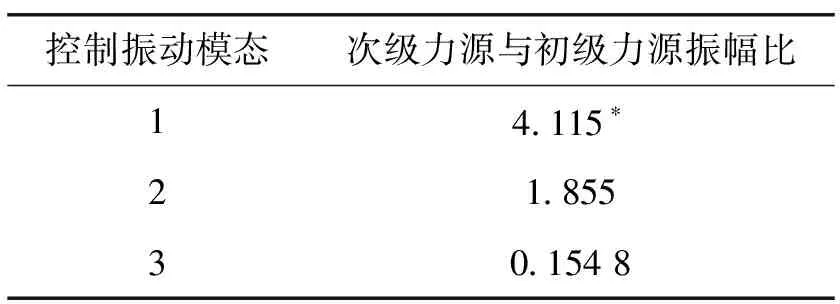
控制振动模态次级力源与初级力源振幅比 14.115∗21.855 30.154 8

表2次级力源的位于(0.02m,3π/4)对应不同模态振动控制次级力源与初级力源的振幅比

Table2Theamplituderatiobetweentheprimaryforceandthesecondaryforcewhenthesecondaryforceisexertedat(0.02m,3π/4)

控制振动模态次级力源与初级力源振幅比 1-6.857 2-3.092 3-0.257 9

结果表明最佳次级声源强度相对于噪声源强度而言,其振幅大小与(rc/rp)成正比;次级声源在该点处产生的声压相位与噪声源在该点处产生的声压相位相差180°。

5 结 语

本文基于弹性板(壳)结构的振动微分方程,并定义板壳之间的连接形式,推导弹性板的弯曲振动以及圆柱壳的径向位移表达式,推导弹性板(壳)-声腔结构耦合振动情况下,外辐射声场指定点的声压表达式。弹性板(壳)结构振动产生的声辐射主要由受力板(壳)的振动产生,并进行了有源力控制研究。算例表明,基于解析方法得到的声压值表达式,便于计算精确的次级力源大小。

[1] J S Yim, D SSohn. Free Vibration of Clamped Free Circular Cylindrical Shell with a Plate Attached at an Arbitrary Axial Position[J]. Journal of Sound and Vibration, 1998, 213(1):75-88

[2] Dowell E H, Gorman G F. Aeoustoelasticity: General Theory, Acoustic Modes and Forced Response to Sinusoidal Excitation, including Comparisons with Experiment[J]. Journal of Sound and Vibration, 1977, 52:519-542

[3] Kim S M, Brennan M J. A Compact Matrix Formulation Using the Impedance and Mobility Approach for the Analysis of Structural Acoustic Systems[J]. Journal of Sound and Vibration,1999, 223(1):97-113

[4] S A Vera, P A A Laura, D A Vega. Transverse Vibrations of a Free Circular Annular Plate[J]. Journal of Sound and Vibration,1999, 224(2): 379-383

[5] Du J T, Li W L, Jin G Y, Yang T J, Liu Z G. An Analytical Method for the In-plane Vibration Analysis of Rectangular Plates with Elastically Restrained Edges[J]. Journal of Sound and Vibration, 2007, 306:908-927

[6] Gorman D J. Exact Solutions for the Free In-plane Vibration of Rectangular Plates with Two Opposite Edges Simply Supported[J]. Journal of Sound and Vibration, 2006, 294:131-161

[7] A Berry, J L Guyader, J Nicolas. A General Formulation for the Sound Radiation from Rectangular, Baffled Plates with Arbitrary Boundary Conditions[J]. Journal of the Acoustical Society of America, 1990, 88(6):2792-2802