季节性商品的二级供应链转运模型研究
李思诺, 邵晓峰
(1. 上海交通大学中美物流研究院, 上海 2000300; 2.上海交通大学,安泰经济与管理学院, 上海 200052)
季节性商品的二级供应链转运模型研究
李思诺1, 邵晓峰2
(1. 上海交通大学中美物流研究院, 上海 2000300; 2.上海交通大学,安泰经济与管理学院, 上海 200052)
以季节性商品供应链为背景, 考虑由一个生产商和二个销售商组成的二级供应链结构, 研究了由生产商的定价决策和销售商的订货决策构成的动态博弈框架, 分析了(1) 转运(不考虑顾客转移)与(2)无转运(顾客部分转移)两种情形下供应链各成员的博弈策略. 数值模拟表明:转运策略的引入, 使生产商的最优期望利润和销售商的最优订货水平得到了提高; 从整体上看, 转运策略增加了总体供应链的最优期望利润.
季节性商品供应链; 转运策略; 订货决策; 定价决策; 顾客转移率
1 引言
供应链管理对生产商和销售商的成本控制、产品质量和服务水平具有重要影响[1]. 在多销售商供应链系统中,特别是季节性商品供应链中, 存在着供应提前期相对较长、未来需求难以准确预测及季末产品残值较低等问题带来的挑战, 由此引出的“转运策略”已受到了产业界和学术界越来越多的关注.
“转运策略”是指各销售商之间通过产品转移来控制成本, 进而实现需求与供给匹配的协调策略. 在多销售商供应链系统中, 当某一销售商自身库存不足时, 若其他销售商有多余库存, 且二者间的转运成本小于其从生产商订货的成本, 则可通过转运来满足顾客需求. 从单个销售商的角度出发, 转运策略是其调节市场需求和自身库存差异的有效途径; 从整个供应链下游的角度来看, 转运策略可以帮助多个销售商实现库存共享, 即通过协调订货策略来减少库存成本, 降低经营风险[2].
在季节性商品市场中转运现象十分常见. 季节性产品包括生命周期较短的电子产品(往往上一代的产品还在热销, 下一代的产品已开始准备生产)、时令性的商品(如月饼、瓜果等)[3]. 与一般商品相比, 这些商品的生产周期与销售周期的比值更大, 销售期间向生产商补货的难度更大. 因此, 季节性商品的单季销售特点使销售商承担着更大的缺货风险和缺货贬值风险, 引入转运机制是十分必要的.
迄今为止, 学术界从不同的角度对转运问题进行了研究. Krishnan 等人(1965)[4]研究了独立需求、集中决策情形下多销售商的转运情况. Needham & Evers(1998)[5]应用数值仿真模拟着重分析影响销售商转运策略的各种变量. Evers(2001)[6]和Minner 等人(2003)[7]分别提出了一种启发式算法来分析多级供应链中分散决策的销售商之间进行转运的条件. 钱宇和陈剑(2008)[8]以医药供应链为背景, 研究了分散决策下的转运补货策略. Zou 等人(2010)[9]在转运模型中提出了“顾客转移率”的概念, 并指出在不同的需求和顾客转移率下转运价格的重要作用.
总的来说, 国内外学者对供应链转运问题的研究已经取得了较为丰富的结果, 但大部分研究只考虑同层级间的转运问题, 而忽略了生产商在转运博弈中的作用[10]; Dong & Rudi (2004)[11]虽然将生产商的行为纳入了模型,但只考虑了转运产生的运输成本, 没有涉及转运价格的研究. 基于此, 本文主要研究将生产商引入博弈框架后转运策略对农产品供应链中各成员期望收益的影响, 以期对我国季节性商品的供应链管理提供参考.
2 模型描述
本文以季节性商品供应链为背景, 建立如下两个模型:
在模型1中, 当销售商i, j一方发生缺货而另一方有货的时候, 假设发生商品转运, 转运的数量不多于缺货数量, 且顾客不发生自行转移. 在模型2中, 当销售商i, j一方发生缺货而另一方有货的时候, 假设不发生转运,且顾客有可能发生自行转移. 单个顾客自行发生转移的概率记为顾客转移率[12], 它跟销售商之间的竞争程度有关. 顾客转移率是外生变量, 分布在0和1之间, 其值越大表明销售商之间的竞争越激烈.
将模型中所用的符号列表说明如下:
y: 销售商i, j的商品售价; w: 销售商i, j的商品进价;
Di,Dj: 销售商i, j的需求水平;Qi,Qj: 销售商i, j的订货水平;
Ri,Rj: 销售商i, j的实际销量;Ui,Uj: 销售商i, j的剩余库存;
Zi,Zj: 销售商i, j的缺货数量;cij,cji: 销售商i, j之间的单位转运价格; Xij,Xji: 销售商i, j之间的转运商品数量;
Hij,Hji: 销售商i, j之间的自行转移的顾客人数;
λij,λji: 一方销售商缺货时, 另一方与缺货方之间的顾客转移率;
h: 销售商的单位库存费用; s: 销售商未售出产品的单位残值;
p: 销售商未满足需求时所受到的单位惩罚; m: 生产商的单位生产成本;
τ: 销售商的单位转运费用;πi,πj: 销售商i, j期望利润;∏: 生产商的期望利润.
为了避免出现“销售商无限量订货”和“销售商不订货”的两种极限情况, 故上述参数应该满足约束条件:. 由于转运价格需要保证在一定范围才对销售商双方都有利, 故上述参数还应满足约束条件:
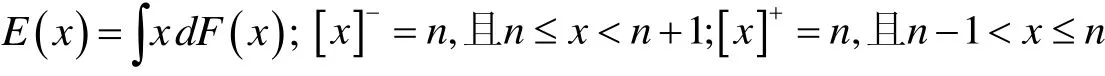
3 转运情形下的决策(模型1)
在模型1中, 考虑转运的情况下, 在一个完整销售周期内, 共有六种供需情形(如图1所示). 事件I是指:销售商i, j均缺货; 事件II是指:销售商j缺货, 销售商i把自己的全部剩余库存转运到j, 但仍不能满足j的需求;事件III是指:销售商j缺货, i根据j的需要转运部分库存到j, 最终两个销售商都满足了顾客需求; 事件IV是指:销售商i, j库存均大于需求; 事件V是事件III的相反情况; 事件VI是事件II的相反情况.
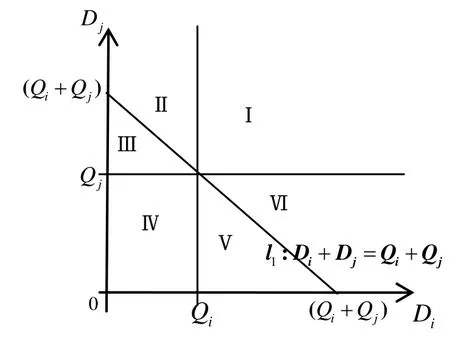
图1 转运情形下的六种事件
模型1是一个完全且完美信息动态博弈模型, 生产商和销售商的决策顺序是:
T=0, 生产商确定商品的批发价格w;
T=1, 销售商根据批发价格制定转运契约, 即确定转运价格cij,cji;
T=2, 销售商根据自己的需求向生产商订货, 即确定订货水平Qi,Qj;
T=3, 销售商在销售时先满足自己顾客的需求, 未满足的部分根据之前签订的转运契约进行补货.
此博弈模型可以利用逆推归纳法来进行求解:首先根据给定的批发价格w和转运价格cij(cji), 销售商会制定期望利润函数值最大的最优订货水平Q*i(Q*j); 然后应用赋值法将转运价格代入Q*i(Q*j)中; 最后将赋值后的Q*i(Q*j) 依次代入生产商的期望利润函数Π中, 计算出使Π取最大值的最优批发价格w*.
3.1 转运情形下的销售商最优订货水平
在转运情形下, 考虑销售商的销售收入、库存商品残值、缺货惩罚、转运收入(支出)、以及商品成本、库存成本后, 销售商i, j的期望利润可表示为:
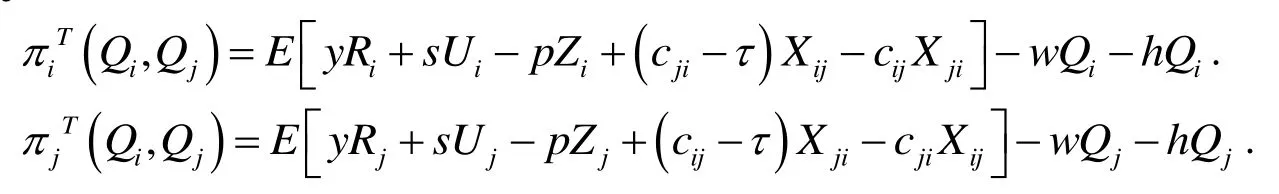
为简化求解过程, 引入以下变量代入后续计算:
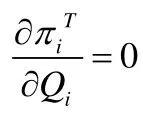
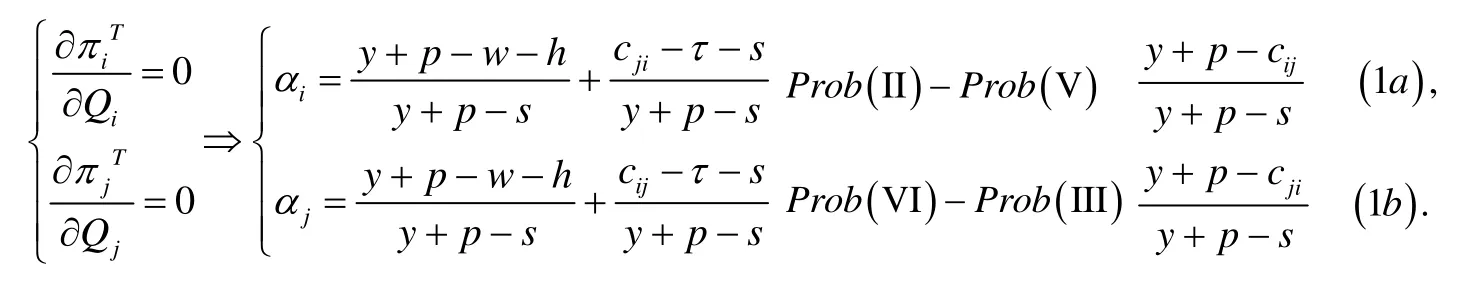
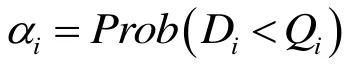
命题1.转运情形下, 假设需求D是连续的随机变量, 保持其他的参数不变, 则销售商i最优订货水平随着单位商品残值s的增大而增大; 同样的,随着批发价格w和单位库存费用h的增大而减小.
为了清楚地分析两销售商的订货水平和批发价格及转运价格的关系, 假设市场需求服从[0,a] 之间的均匀分布, 而且相互独立, 即
根据对称性应有:
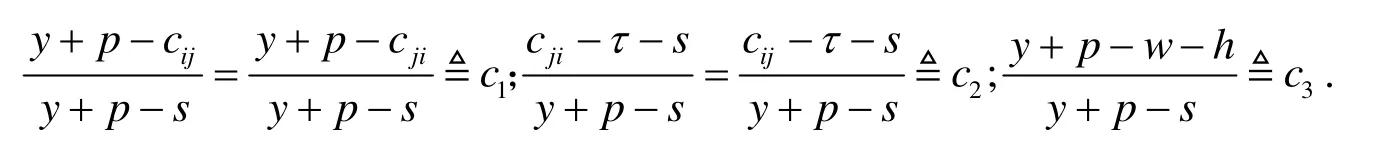
求解方程组(1a)(1b)后应有:
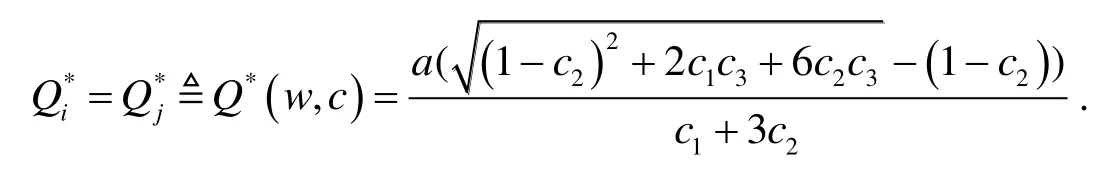
3.2 销售商之间的最优转运价格
如果转运价格很高, 则销售商会选择在期初提高订货水平; 如果转运价格很低, 销售商会选择期末获取产品残值. 因此转运应满足条件:
为了研究的方便, 将区间内的值取整得序列:
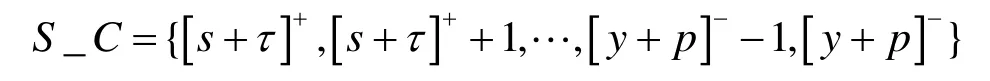
将序列S_C中的转运价格c依次代入两种情形下的销售商最优订货水平Q*(w,c)中, 即得到关于批发价格w的最优订货水平序列S_Q*(w).
3.3 转运情形下最优批发价格
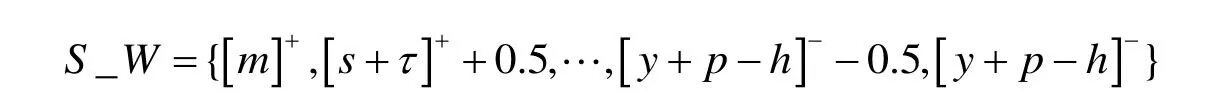
命题3.转运情形下, 将批发价格和转运价格的定义域离散化之后, 生产商的批发价格、销售商的转运价格和订货水平肯定存在最优解.
证明:将批发价格和转运价格的定义域离散化之后, 生产商和销售商的期望利润都是有限集, 那么它们的最优期望利润肯定存在, 该期望利润对应的批发价格、转运价格和订货水平即为最优解.
模型1 是建立在后续阶段各博弈方理性选择的基础上, 自然排除了包含不可信的威胁或承诺的策略选项,因此得出的策略组合具有稳定性.
4 无转运情形下的决策(模型2)
与考虑转运的模型类似, 在无转运的情形下, 考虑一个完整的销售期间, 将会有如下六种情况发生(如图2所示):
事件A是指:销售商i, j都是因需求等大:川于西库獐存牙导菜致多缺糖货的提, 取概及率含记量为测P定rob(I); 事件B是指:销售商j因需求大于库存导致缺货, 原本是j的部分顾客自行转移到i处, 但i的剩余库存不能满足转移过来的全部顾客需求, 概率记为Prob(II-1); 事件C是指:销售商j因需求大于库存导致缺货, 原本应是j的部分顾客自行转移到i处, 且销售商i的剩余库存能满足转移过来的全部顾客需求, 概率记为Prob(II-2)+Prob (III); 事件D是指:销售商i, j均需求小于库存, 概率记为Prob(IV); 事件E与事件C对应, 概率记为Prob(V)+Prob(VI-2); 事件F与事件B对应, 概率记为Prob(VI-1).

图2 无转运情形下的六种事件
模型2也是一个完全且完美信息动态博弈模型, 生产商和销售商的决策顺序与模型1类似, 但少了期初确定转运价格和期末根据契约转运的环节. 类似的, 仍然可以采用逆推归纳法来求解模型2.
T=0, 生产商确定商品的批发价格w;
T=1, 销售商根据自己的需求向生产商订货, 即确定订货水平Qi,Qj;
T=2, 销售商在销售时先满足自己顾客的需求, 剩余库存用于满足自行转移过来的顾客需求.
4.1 无转运情形下的销售商最优订货水平
在无转运情形下, 考虑销售商的销售收入、库存商品残值、缺货惩罚、以及商品成本、库存成本后, 销售商i, j的期望利润可表示为:

求分别关于Qi,Qj的一阶偏导数, 利用在模型1中的中间变量来简化模型, 得无转运情形下最优订货水平,所在的方程组:
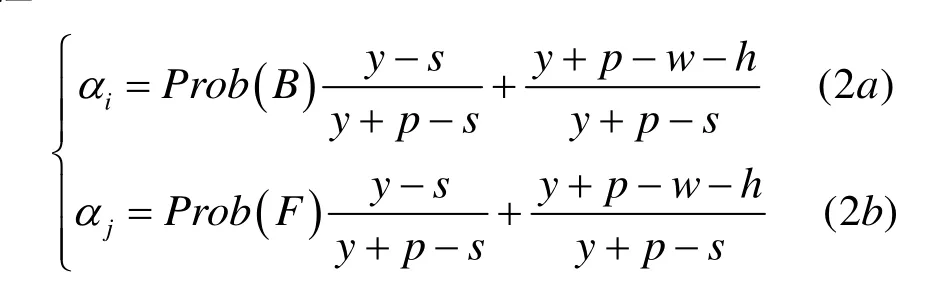
接下来的分析与转运情形下的分析类似, 假设需求Di是连续的随机变量, 则αi=Prob(Di 命题4.无转运情形下, 假设需求D是连续的随机变量, 保持其他的参数不变, 则销售商i最优订货平随着单位商品残值s的增大而增大; 同样的,随着批发价格w和单位库存费用h的增大而减小. 4.2 无转运情形下最优批发价格 求解过程与模型1类似, 首先采用同样的方法对批发价格w进行离散化得到w的序列. 再将Q*(w)代入到生产商的期望利润函数中:Π=2(w-m)Q*(w),在w的序列中求解这个一元函数的最优化问题, 从而确定最优的批发价格w*和最优的生产商期望利润Π. 命题5.无转运情形下, 将批发价格的定义域离散化之后, 生产商的批发价格和销售商的订货水平肯定存在最优解. 证明略. 为了更加清晰地展示模型的结果, 本文进行了数值模拟, 讨论了在转运情形和无转运情形下, 生产商的批发价格、销售商的订货量和两者期望利润等变量的对比情况. 根据模型1的决策分析, 转运情形下生产商的最优批发价格、最优期望利润和销售商的最优转运价格、最优订货水平和最优期望利润分别是: 根据模型2的决策分析, 无转运情形下生产商的最优批发价格、最优期望利润和销售商的最优订货水平和最优期望利润分别是: 可以看出, 引入转运策略后, 生产商的最优期望利润提高了, 销售商的最优订货水平也提高了, 销售商的最优期望利润降低了, 但是供应链整体的期望利润提高了. 同时, 生产商的最优期望利润要远高于销售商的最优期望利润, 生产商可以拿出一部分利润补偿给销售商, 从而使供应链的运作更稳定协调. 本文在整个供应链系统内信息是完全对称的前提条件下, 以季节性商品供应链为背景, 建立了一个生产商和二个销售商的二级供应链模型, 研究了供应链成员在各阶段的最优定价和订货的决策问题. 结果显示转运情形下销售商的最优期望利润高于不考虑转运的情形, 因此销售商会在期初签订转运契约, 但对于生产商设置的最优批发价格, 生产商获得了极大的利润但销售商却很有可能会遭受损失, 而且此时的最优转运价格也是处于最高点的, 这使得转运策略在销售商应对紧急缺货时的协调能力明显下降. 本文的研究在未来还可以有若干扩展, 例如在(0,1)之间为顾客转移率选取不同的参数值, 研究多种竞争强度下销售商与生产商的博弈问题; 还能研究生产商从供应链整体利润最大的角度去选择最优批发价格的问题,如果整体利润因此提高了, 再近一步研究如何在生产商和销售商之间进行利润重分配. [1] GRAHOVAC J, CHAKRAVARTY A. Sharing and Lateral Transshipment of Inventory in a Supply Chain with Expensive Low-Demand Items[J]. Management Science, 2001, 47(4): 579-594. [2] 温涛, 黄培清. 转运情形下基于订单的缺货水平分析[J]. 工业工程与管理, 2007,12( 5):1-10. [3] 蔡建湖, 周根贵, 邵祖峰. 季节性商品供应链的库存管理战略研究[J]. 商业研究, 2009, 2:1-5. [4] KRISHNAN K S, RAO V R K. Inventory control in N warehouses[J]. Journal of Industrial Engineering, 1965, 16(3): 212-215. [5] NEEDHAM P M, EVERS P T. The influence of individual cost factors on the use of emergency transshipments[J]. Transportation Research, 1998, 34(2): 149-160. [6] EVERS P T. Heuristics for assessing emergency transshipments[J]. European Journal of Operational Research, 2001, 129(2): 311-316. [7] MINNER S, SILVER E A, ROBB D J. An improved heuristic for deciding on emergency transshipments[J]. European Journal of Operational Research, 2003, 148(2): 384-400. [8] 钱宇, 陈剑. 供应链中考虑下游转运的订货和定价决策研究[J]. 中国管理科学, 2008, 16(1) :53-59. [9] ZOU L, DRESNER M, WINDLE R. A two-location inventory model with transshipments in a competitive environment[J]. International Journal of Production Economics, 2010, 125(2): 235-250. [10] 陈剑, 徐鸿雁. 基于销售商努力的供应商定价和生产决策[J]. 系统工程理论与实践, 2009, 29(5): 1-10. [11] DONG L, RUDI N. Who Benefits from Transshipment? Exogenous vs. Endogenous Wholesale Price[J]. Management Science, 2004, 50(5): 645-657. [12] KEAVENEY S M. Customer Switching Behavior in Service Industries: An Exploratory Study[J]. Journal of Marketing, 1995, 59(2): 71-82. Research on two-stage transshipment model in supply chain with seasonal products LI Si-nuo1, SHAO Xiao-feng2 This paper analyses a two-stage supply chain with seasonal products. It contains one manufacturer and two retailers to analyze the manufacturer’s pricing decision and the retailers’ ordering decision processes. Two dynamic game models are established, i.e. transshipment without consumers’ switching and no transshipment with partial consumers’ switching. Numerical analyses suggest that transshipment may increase the optimal expected profit of manufacturer and optimal order quantity of retailers, and the optimal expected profit of the whole supply chain. supply chain of seasonal products; transshipment; ordering decision; pricing decision; customers’ switching rate F25 A 1003-4271(2014)02-0306-06 10.3969/j.issn.1003-4271.2014.02.26 2013-12-13 李思诺(1989-), 女, 硕士研究生; 邵晓峰(1973-), 男, 教授, 研究方向: 供应链管理.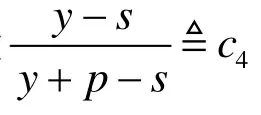

5 数值分析与讨论
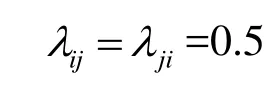
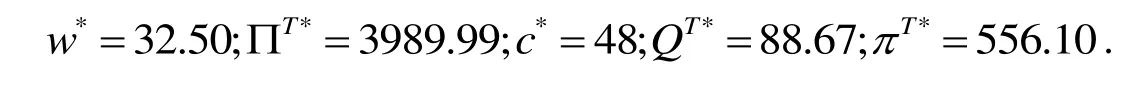
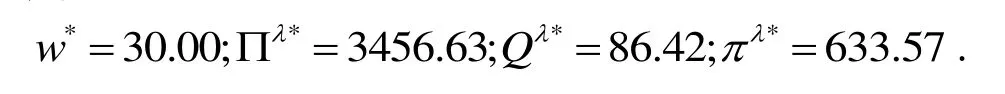
6 结论与展望
(1. Sino-US Global Logistics Institute, Shanghai Jiao Tong University, Shanghai 200030, P.R.C.; 2. Aantai College of Economy and Management, Shanghai Jiao Tong University, Shanghai 200052, P.R.C.)

