ZnGa2Se4:V3+光谱的理论研究
李东阳, 杜懋陆
(1. 西南民族大学预科教育学院, 四川 成都 610041; 2. 西南民族大学电信学院, 四川 成都 610041)
ZnGa2Se4:V3+光谱的理论研究
李东阳1, 杜懋陆2
(1. 西南民族大学预科教育学院, 四川 成都 610041; 2. 西南民族大学电信学院, 四川 成都 610041)
应用区分t2和e轨道共价性的差异(包含静电部分和晶场部分)并考虑了低对称场的能量矩阵, 在考虑和忽略静电参量B00的条件下, 分别研究了t2和e轨道共价性的差异对三元半导体ZnGa2Se4:V3+能级以及低对称分裂的影响; 计算了ZnGa2Se4:V3+晶体的能级的低对称分裂, 并与实验值进行比较. 计算结果与实验值符合很好. 研究发现: 在对ZnGa2Se4:V3+晶体的光学性质进行理论研究时, 在能量矩阵的静电和晶场部分同时考虑t2和e轨道共价性的差异是非常有必要的; 晶场参量B00对ZnGa2Se4:V3+的能级有重要影响, 因此不能忽略.
V3+; ZnGa2Se4; 光谱
1 引言
含有过渡金属离子的II-III2-VI4族三元半导体在光电器件方面具有广阔应用前景, 从而成为理论和实验研究者的焦点. 具有四角对称结构的ZnGa2Se4半导体[1-2], 作为典型的II-III2-VI4族三元半导体, 也倍受研究者的关注. 在实验方面, Kim 等[3]开展了V3+掺ZnGa2Se4晶体的光谱实验, 测到V3+掺ZnGa2Se4晶体的光谱. 在理论方面, 传统的晶体场理论因忽略了t2和e轨道共价性的差异, 对共价性很强的半导体已不再适用. 在能量矩阵的静电部分引入不同的共价因子来区分t2和e轨道共价性的差异的工作已取得了一定的成功[4-7]. 然而, 这种方法忽略了晶场部分的t2和e轨道共价性的差异, 从而导致晶场参量B00对能级的影响被忽略. 此外, 由于低对称局域结构会导致立方对称能级的进一步分裂, 中心金属离子的局域对称结构也是研究晶体中过渡金属离子光学性质时必须考虑的因素[8]. 因此, 对ZnGa2Se4:V3+光谱的理论分析应同时考虑t2和e轨道共价性的差异(包含静电部分和晶场部分)和低对称场的影响. 然而, 迄今却鲜有相关报道见于刊物.
本文应用区分t2和e轨道共价性的差异(包含静电部分和晶场部分)并考虑了低对称场的能量矩阵, 在考虑静电参量B00和忽略静电参量B00两种条件下, 研究了t2和e轨道共价性的差异对三元半导体ZnGa2Se4:V3+能级及能级分裂的影响. 计算了ZnGa2Se4:V3+晶体的四角对称分裂能级, 并与实验值进行比较. 计算结果与实验值符合很好.
2 t2和e轨道共价性差异对V3+:ZnGa2Se4晶体能级的影响
V3+:ZnGa2Se4晶体具有很强的共价性, 并具有四角对称结构, 所以对ZnGa2Se4:V3+光谱的理论研究需要同时考虑t2和e轨道共价性的差异(包含静电部分和晶场部分)和低对称场的影响. 文献[8]提供了区分t2和e轨道共价性的差异(包含静电部分和晶场部分)并考虑了低对称场的能量矩阵. 在该能量矩阵中,t2和e轨道共价性的差异通过共价参量Nt和Ne来描述. 在传统的能量矩阵中, 晶场参量B00项总是能在计算中被相互抵消; 考虑了t2和e轨道共价性的差异之后, 能量矩阵中与晶场参量B00项的系数不相同, 在计算中不再能被抵消. 在忽略、考虑晶场参量B00两种情况下, 我们分别讨论t2和e轨道共价性的差异对ZnGa2Se4:V3+晶体能级的影响.
Nt和Ne之间差异程度在八面体坐标下可用参量ε描述为:


显然, 当Nt和Ne之间差异增大时,ε也随着增大; 反之, 当Nt和Ne之间差异减小时,ε也随着减小. 应用文献[8]提供的能量矩阵, 我们可以得到ZnGa2Se4:V3+晶体能级随着参量ε变化的图像, 如图1中(a)和(b)所示. (a)和(b)分别描述了晶场参量B00=0和B00≠0的时, 能级随着参量ε的变化情况. 由于四角对称下能级数目太多, 在此我们只选三重态能级进行讨论. 对比(a)图和(b)图, 容易看出B00=0和B00≠0时, 能级随着ε变化的趋势大不相同. (a)图中(晶场参量B00=0), 随着ε的增加, 能级不断减小; (b)图中(晶场参量B00≠0), 情况却完全相反: 随着ε的增加, 能级也随之增加.
晶场参量B00除了对能级有不可忽略的作用以外, 对能级的分裂也有重要影响. 我们知道D4对称下的能级3A2和能级3E是由立方对称下3T1对应组态分裂而成, 因此由(a)图很容易看出(晶场参量B00=0), 当对称性从立方对称降低至D4对称时,ε的变化对3T1能级的低对称分裂值影响很小, 而在(b)图中, 即晶场参量B00≠0时,随着ε的增加3T1能级的低对称分裂值明显在增加. 因此在研究ZnGa2Se4:V3+晶体的光学性质时, 在晶场矩阵部分考虑t2轨道和e轨道共价性的差异是非常有必要的; 在共价晶体中, 晶场参量B00对能级以及能级的分裂都有重要的贡献, 因而不能忽略.
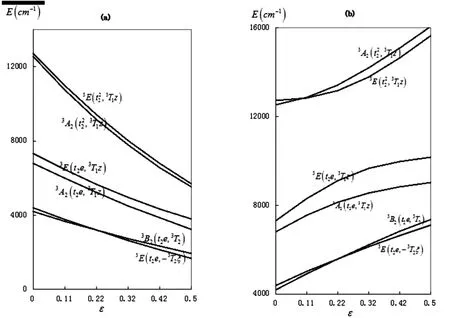
图1 ZnGa2Se4:V3+晶体能级随着参量ε的变化. 图a中, 晶场参量B00=0; 图b中, 晶场参量B00=15000cm-1.3 ZnGa2Se4:V3+晶体的能级
文献[1]和[2]提供了ZnGa2Se4晶体Zn-Se键键长2.44Å, 键角54°. 由于晶场参量B00与键角无关, 可由立方场下的能级拟合得出ZnGa2Se4:V3+共价参量和晶场参量分别为:

应用所获得的参数和能量矩阵[8], 可计算D4对称下ZnGa2Se4: V3+晶体的能级如表2所示. 计算结果与实验值符合得很好.

表1 ZnGa2Se4:V3+晶体的能级
3 小结
本文利用区分t2和e轨道共价性的差异(包含静电部分和晶场部分)并考虑了低对称场的能量矩阵, 在考虑和忽略静电参量B00的条件下, 研究了t2和e轨道共价性的差异对ZnGa2Se4:V3+晶体能级和低对称分裂的影响. 计算了ZnGa2Se4:V3+晶体的能级的低对称分裂, 并与实验值进行比较. 计算结果与实验值符合得很好.

参考文献:
[1] ERRANDONEA D, KUMAR R S, MANJON F J, et al. High-pressure x-ray diffraction study on the structure and phase transitions of the defect-stanniteZnGa2Se4and defect-chalcopyrite CdGa2S4[J]. Journal of Applied Physics, 2008, 104(6): 63524-63529.
[2] HANADA T, IZUMI F, NAKAMURA Y, et al. Neutron and electron diffraction studies ofZnGa2Se4[J]. Physica B: Condensed Matter, 1997, 241: 373-375.
[3] KIM Y G, LEE C. Optical absorption of vanadium dopedZnGa2Se4single crystals[J]. Journal of Applied Physics, 1998, 83(12): 8068-8070.
[4] DU M L, YEOM T H. Energy levels of the d{*8}electron and d{*2}hole system[J]. Physical Review B, 1999, 59(7): 4881-4887.
[5] CHEN J J, DU M L. Theoretical investigation of the optical spectrum and gyromagnetic factor for GaAs: Co2+, [J]. Physica B: Condensed Matter, 2001, 305(3): 264-269.
[6] ZHOU Y Y, LI F Z. Excitation levels, fine-structure splittings of ground state and EPR parameters in ZnSe: Cr2+[J]. Journal of Physics and Chemistry of Solids, 1998, 59(6): 1105-1110.
[7] DONG-YANG L, MAO-LU D, YI H. The covalence effect of energy levels of Mn2+in ZnS[J]. Physica B: Condensed Matter, 2013, 415: 5-9.
[8] LI DONG-YANG, DU MAO-LU. The covalent effect on the energy levels of d2ions in tetragonal crystal[J]. Physica B: Condensed Matter, 2013 (DOI:10.1016/j.physb.2013.09.014).
Theoretical study on the absorption spectra for ZnGa2Se4:V3+
LI Dong-Yang, DU Mao-lu
(Southwest University for Nationalities, Chengdu 610041, P.R.C.)
This paper uses the energy matrix, considers the different covalence of t2and e orbitals in both the electrostatic repulsions and the crystal-field potential and the influence of low symmetry field, while taking and not taking the crystal field parameter B00into account, the effects of the covalence on the energy levels ofZnGa2Se4:V3+are investigated, respectively. The low symmetry splitting levels ofZnGa2Se4:V3+are calculated, and compared with the experimental data. It is found that the different covalence of t2and e orbitals in both electrostatic repulsions part and crystal-field potential part should be considered when the optical properties ofZnGa2Se4:V3+are studied; the crystal field parameter B00has an important contribution to the low symmetry splitting levels ofZnGa2Se4:V3+, and cannot be neglected. The calculated results are in good agreement with the experimental data.
V3+;ZnGa2Se4; absorption spectra
O48
A
1003-4271(2014)02-0261-04
10.3969/j.issn.1003-4271.2014.02.18
2013-10-11
李东阳(1983-), 男, 讲师, open_please@163.com.
中央高校基本科研业务费专项项目(11NZYQN37).

