基于遗传算法的组网雷达优化部署∗
张 远,方 青,曲成华
(中国电子科技集团公司第三十八研究所,安徽合肥230088)
0 引言
雷达组网预警探测系统通过融合不同体制、不同功能、不同频段的多雷达情报,实现整体探测和情报共享,具有很强的反隐身、抗干扰、反低空/超低空突防、抗摧毁能力,极大地提高了现役雷达的作战效能。雷达网功能的发挥,依赖于各组网雷达在空间和频率上的分布关系,优化部署是实现雷达网作战效能倍增的前提和基础。目前雷达网优化部署研究主要集中于全局未知时的雷达网部署,采用的方法主要是枚举法、专家推理法和遗传算法等[1-3],枚举法和专家推理方法存在组合爆炸和执行速度较慢等缺点,当组网雷达数较多时,几乎不可能得到优化部署方案;另外这些方法均未考虑在实际雷达部署中的限制条件,部署结果的可用性不足。本文基于遗传算法的雷达网优化部署方法结合GIS(地理信息系统)信息,在充分考虑雷达部署的各种限制条件基础上,采用遗传算法,通过一定数量的染色体群世代更迭,优胜劣汰,能较快地使部署接近最优(次优)解,避免了枚举法的执行速度慢和专家推理法的组合爆炸问题。
1 基于遗传算法的雷达组网优化部署原理
1.1 组网雷达优化部署的原则
组网雷达优化部署的目的是实现雷达网的无缝、连续覆盖,通过多重覆盖提高目标发现概率和目标更新数据率,因此组网雷达优化部署应该遵循连续性、严密性和重叠性的原则。
连续性:在雷达网探测区域内,目标的发现概率大于要求的门限值,目标能连续跟踪。
严密性:部署完成后,要求的探测空域在各高度层上均能被完全覆盖,不存在探测空洞和盲区。
重叠性:雷达网具备一定的重叠区域,达到雷达组网性能倍增的目的,实现雷达组网的功能。
为满足上述部署原则,因此雷达配置必须满足下列四个要求:
(1)高、中、低与远、中、近距离探测一体化,保障雷达网威力覆盖的连续性、严密性;
(2)警戒与保障引导一体化,保证雷达网警戒与保障的威力范围;
(3)频率与空间一体化,满足系统整体抗干扰、反隐身的功能要求;
(4)机动、隐蔽与防护一体化,保障系统的机动、隐蔽、雷达接入和提高防护能力。
1.2 优化部署约束条件
雷达组网的优化部署是一个多约束条件的优化问题,即雷达部署必须满足下列条件:
(1)雷达站位置相对固定,雷达只能部署在雷达站;
(2)雷达站地形、地貌条件,如雷达站可以部署的雷达数量;
(3)雷达站通信条件;
(4)雷达数量和种类相对固定,雷达种类和数量的选择不能超过该范围;
(5)雷达部署与配置的四个一体化要求。
在采用遗传算法进行寻优时,将约束条件作为子代生成的前提,即在初始种群生成、交叉、变异等操作时,只能从合法(满足约束条件)的父代中生成新的合法子代,将有约束条件的优化问题转化为无约束的优化问题[4-7]。
1.3 优化部署的目标函数
组网雷达优化部署的目的是充分发挥多雷达在空间、频率上的互补和倍增优势,提高雷达网的整体探测性能,因此组网雷达优化部署应该达到的目的包括:在保证雷达网覆盖连续性、严密性和重叠性的基础上,提高隐身目标、小目标、低空目标、高速高机动目标的探测能力;提高目标的综合抗电子干扰能力;提高目标定位跟踪精度;在不浪费雷达资源的条件下,充分发挥雷达网的整体探测优势,因此,组网雷达优化部署的目标函数可以定义为
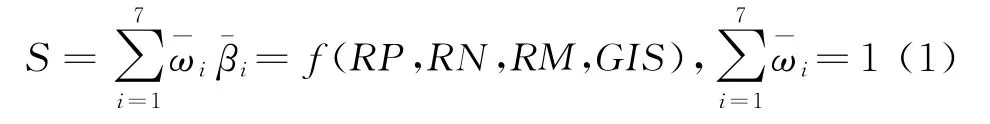
式中,RP为雷达部署位置;RN为部署雷达数量;RM为部署雷达型号;GIS为雷达阵地条件;为评价因子权系数(可根据雷达网主要作战意图改变);为相应的雷达网性能评价因子的归一化值。雷达网性能评价因子包括:
(1)严密性评价因子β1
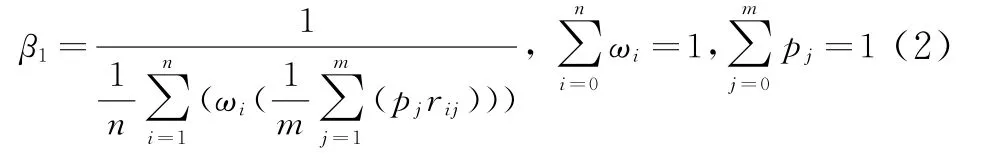
式中,n为高度采样数;m为方位采样数;ωi为高度层i的盲区等效半径重要性系数;p j为高度层i中第j个方位的盲区等效半径重要性系数;r ij为高度层i中第j个采样方位的盲区等效半径。严密性评价因子衡量雷达网覆盖是否有盲区或空洞。
(2)连续性评价因子β2
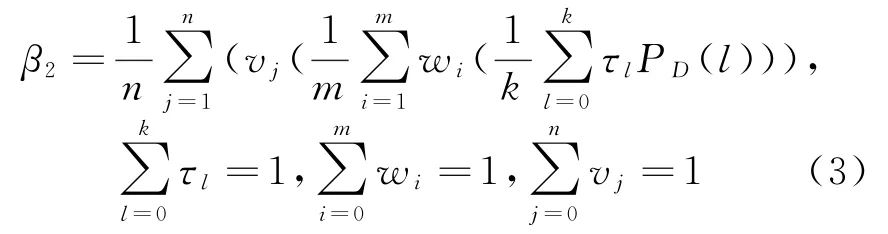
式中,k为距离采样数;w i为高度层j中第i个采样方位的发现概率重要性系数;τl为同一方位上的每个采样点的发现概率重要性系数;P D(l)为每个采样点对典型目标的发现概率。连续性因子衡量雷达网目标连续探测和跟踪的范围。
(3)重叠性评价因子β3
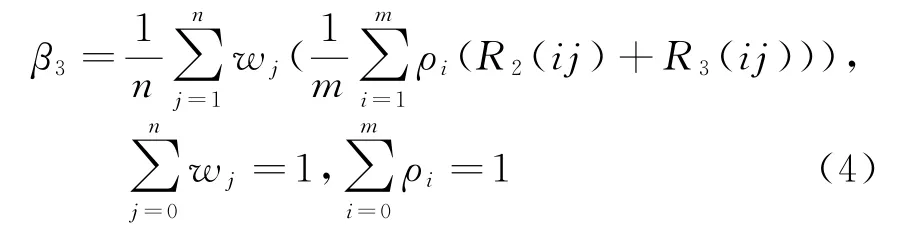
式中,w j为高度层j的重叠区域等效半径重要性系数;ρi为高度层j中第i个方位的重叠区域等效半径重要性系数;R2(ij),R3(ij)分别为高度层i中第j个采样方位的二重、三重重叠区域的等效半径。重叠性因子衡量雷达网重叠区域的大小。
(4)目标探测能力评价因子β4

式中,φk为低空目标、隐身目标、小目标和高速高机动目标探测能力的权系数;β4k分别为低空目标、隐身目标、小目标和高速高机动目标探测能力,定义为
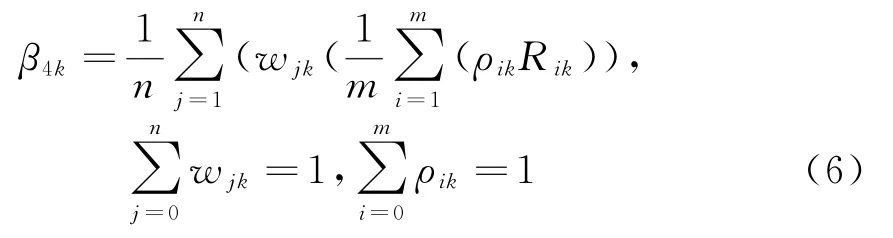
其中,w jk为高度层j的探测距离重要性系数;ρik为高度层j中第i个采样方位的探测距离重要性系数;R ik为第i方位上对典型目标的探测距离。目标探测能力评价因子衡量雷达网对低空目标、隐身目标、小目标和高速高机动的探测能力。
(5)抗干扰能力评价因子β5

式中,ε=m/n为空域抗干扰能力因子;为频域抗干扰能力评价因子,其中fmax为网中雷达的最高频率,fmin为网中雷达的最低频率,B0为实际雷达频带宽度,p为雷达网的频率重叠系数。抗干扰能力评价因子通过空间和频域抗干扰能力衡量雷达网的综合抗电子干扰能力。
(6)探测精度评价因子β6

式中,w j为高度层j的探测距离重要性系数;ρi为高度层j中第i个采样方位的探测距离重要性系数;R i为第i方位上探测圆精度小于500 m的最大距离。探测精度评价因子衡量雷达网目标定位的精度。
(7)资源使用率评价因子β7

资源使用率评价因子衡量雷达网资源使用,目的是在保证雷达网作战效能的基础上,尽量节省雷达资源。
2 基于遗传算法的雷达组网优化部署算法结构
2.1 初始种群生成
在雷达组网中,雷达与阵地之间的组合关系是所求问题的信息,各雷达阵地采用符号编码方法,m个阵地对应的编码分别为(1,2,3,…,m),则n个雷达与m个阵地之间的组合关系如表1所示。
因此,每个雷达的阵地编号即为一个染色体编码,n个雷达的部署就可以形成一个染色体串(P1,P2,…,P i,…,P n),其中

若雷达R i对应的雷达站编号P i为0,则表示该雷达不部署在任何阵地,一个染色体串形成一种部署方案。
随机生成l个满足约束条件要求的部署方案{A1,A2,…,A k,…,A l},其中A k=(P1k,P2k,…,P ik)[7-8],用这l种部署预案组成遗传算法的初始种群。
各种群的适应度函数设计为式(1),直接采用优化部署的目标函数计算各种群适应度,衡量部署方案的优劣。
2.2 选择
选择是根据适者生存的原则选择生成下一代个体(方案)的父本,以适应度为选择原则,选择出适应度大的部署方案直接传给下一代,并淘汰劣质方案。
由适应度计算每种方案的被选择概率,第i个部署方案被选择参与下一代种群的概率为

为增加适应度高的个体被选择的概率,采用轮盘赌式的正比选择法,即产生一个取值范围在0和之间的均匀分布的随机数r,选择满足式(12)的第i个部署方案作为匹配集。

为保证遗传算法的收敛性,保证最优个体不被破坏,能够被复制到下一代,采用最优保存策略,即将适应度最高的个体替换下一代个体中适应度最差的个体,这样适应度最高的个体能保存到下一代种群中。
2.3 交叉
采用一点交叉的方法进行交叉操作,在被选中用于繁殖下一代的个体中,以交叉概率pc生成一个“一点交叉”的交叉位,随机不重复的从中间群体中选择两个个体,对交叉位以后的基因进行交叉运算,直到中间群体中所有的个体都被选择过,交叉过程必须满足部署方案的约束条件,过程如图1所示。
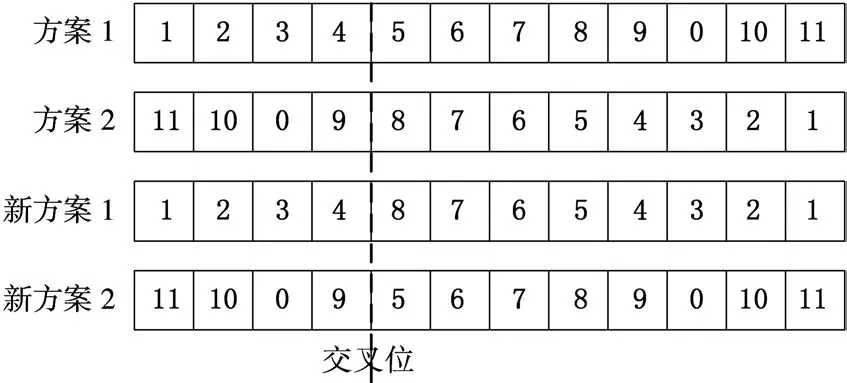
图1 交叉操作示意图
方案1和方案2交叉后,方案1的前半部分和方案2的后半部分结合形成新方案1,方案1的后半部分与方案2的前半部分结合形成新方案2。
2.4 变异
变异是在交叉后的个体中,以变异概率p m对所有个体的基因位进行变异运算,随机产生一个0~m之间的自然数赋值给该位,生成子代群体。图2为变异生成新方案的过程。
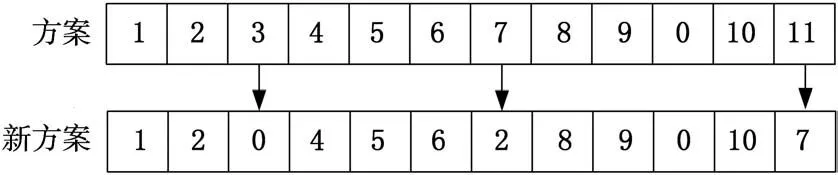
图2 变异操作示意图
变异生成的新个体必须满足雷达网部署的约束条件。
3 算法流程
基于遗传算法的组网雷达优化部署算法流程如图3所示。
(1)根据雷达类型、数量、阵地数量,确定染色体编码的长度;
(2)按约束条件随机生成N个方案作为初始种群;
(3)根据实际情况计算每种方案的适应度值,并根据适应度值确定每种方案的被选择概率,并进行排序;
(4)根据排序结果,利用遗传算法的选择、交叉、变异等操作准则进行群体更新,形成新一代的群体;
(5)停止准则,当最优个体的适应度和群体适应度不再上升,或达到预定的迭代次数,结束算法,输出结果。
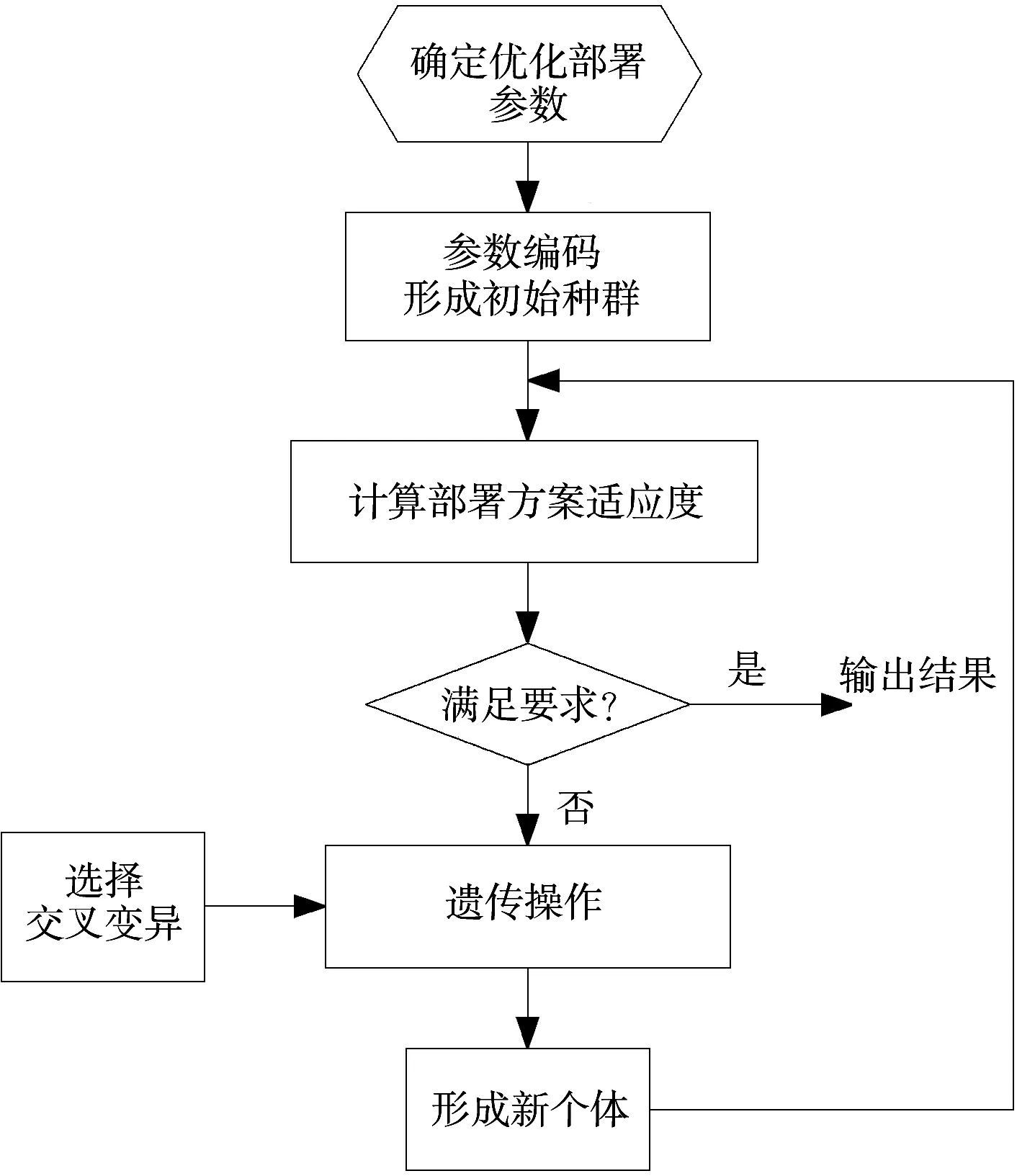
图3 优化部署算法流程
4 算法仿真
根据前面的算法,选取7型雷达,7个阵地进行部署,各雷达阵地的约束条件如表2所示。
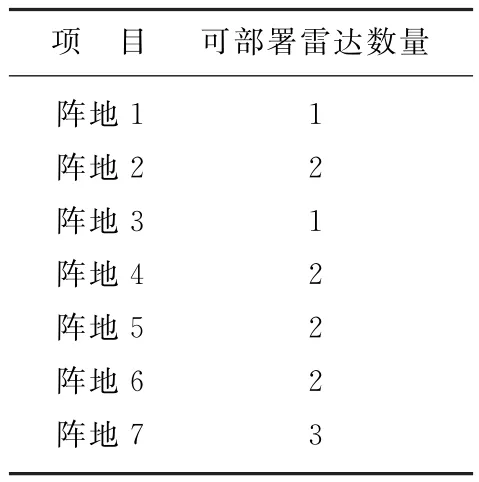
表2 约束条件表
仿真雷达探测威力参数如表3所示。

表3 仿真雷达参数
取初始种群数量为N=50,按约束条件随机生成初始方案50个,交叉概率pc=0.6,变异概率pm=0.05,经过100次的迭代,仿真结果如表4所示。
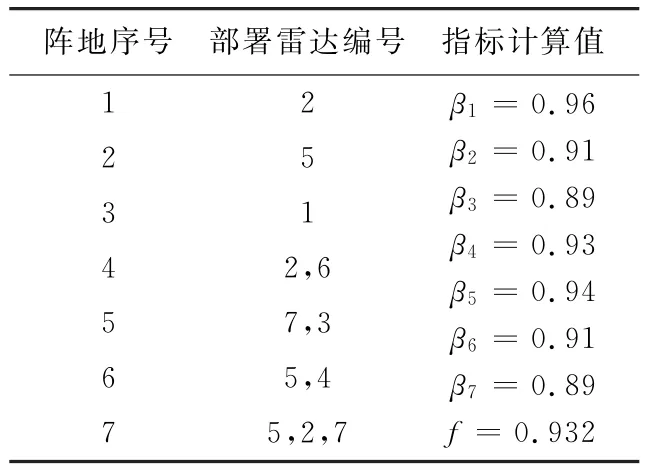
表4 仿真雷达参数
探测威力效果如图4所示,该部署方案的综合探测性能最佳,其目标函数值最大,在各高度层,雷达网覆盖满足连续性、严密性和重叠性要求,同时满足雷达配置的四个一体化要求。仿真结果表明:基于遗传算法的组网雷达优化部署方法能达到最优或准最优解,算法的执行速度比枚举法有明显的提高;不存在知识的组合爆炸问题,是一种有效的雷达网优化部署方法。
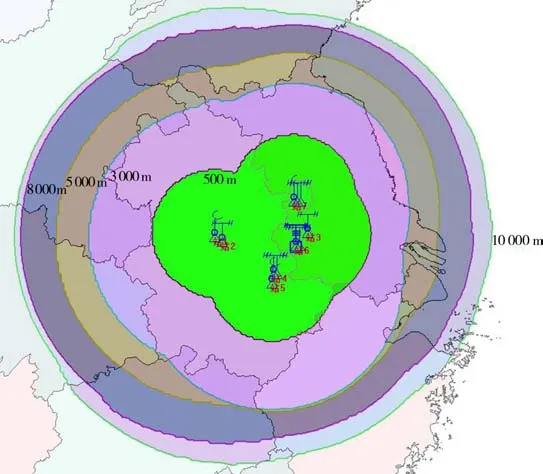
图4 优化方案覆盖效果
5 结束语
雷达组网是提高雷达系统整体探测性能,获取信息优势的有效手段,基于遗传算法的组网雷达优化部署方法为组网雷达优化部署提供了一种在解空间寻优的方法,该方法原理简单,寻优速度快,应用灵活,是解决雷达组网中优化部署问题的一种比较好的方法。为进一步提高算法的收敛性和收敛速度,需要在优化目标函数和交叉概率、变异概率等方面作进一步的研究。
[1]阙渭焰,彭应宁.数据融合与雷达优化布站[J].系统工程与电子技术,1996(12):26-32.
[2]卢金涛,杨瑞娟,熊祝平.雷达阵地选择的多目标决策方法[J].空军雷达学院学报,2003,17(1):13-15.
[3]莫建文,韩传久,张彤.遗传算法在雷达组网最优布阵中算法研究[J].信息技术,2005(3):66-68.
[4]Fogel D B.A Comparison of Evolutionary Programming and Genetic Algorithms on Selected Constrained Optimization Problems[J].Simulation,1995,64(6):397-404.
[5]Homaifar A,Qi C L,Lai S H.Constrained Optimization via Genetic Algorithms[J].Simulation,1994,62(4):242-253.
[6]Youssef H,Sait S M,Adiche H.Evolutionary Algorithms,Simulated Annealing and Tabu Search:a Comparative Study[J].Engineering Application of Artificial Intelligence,2001,14(2):167-181.
[7]张远,曲成华,戴谊.基于遗传算法的雷达组网误差配准算法[J].雷达科学与技术,2008,6(1):65-68.ZHANG Yuan,QU Cheng-hua,DAI Yi.Registration Algorithm for Radar Netting Based on Genetic Algorithm[J].Radar Science and Technology,2008,6(1):65-68.(in Chinese)
[8]苟先太,金炜东.有约束优化中遗传算法的应用[J].西南交通大学学报,1997,32(4):433-437.

