基于UG 的天线座模态与应力分析

张守银，张 翔，张 琳

(北方通用电子集团有限公司 专业6 部，陕西 西安 710100)

天线座是支撑天线探测目标的装置［1］。在雷达通讯设备，尤其是大型、精密的设备中，天线座对整个设备的精度、可靠性、成本和加工周期影响较大，整机的性能指标在较大程度上取决于天线及天线座的结构设计和制造工艺水平。天线座结构要求重量轻、刚度大，承受载荷有雷达及自身的重力、伺服系统的激励载荷以及风荷、颠簸等随机载荷作用［2］。为防止天线座结构的风激振动和避免结构固有频率落在伺服带宽之内，保证天线的指向精度和提高天线抵抗外界干扰的能力，天线座结构除了满足静力要求外，对结构的动态特性也有一定要求［3］。本文使用UGNX/CAD 模块建立了某型雷达天线座转台的三维模型，并使用UGNX/Nastran 结构分析模块进行了模态分析，得到了该转台的固有频率和相应的振型，在设计的初期充分认识了结构的固有频率特性和刚度分布等情况，并指导了对模型的进一步优化设计。这种基于初步模型的模态分析，可在设计阶段就预知产品性能，缩短设计周期，节省大量的时间和物力，并有效地提高产品的可靠性，为该天线座转台的设计优化和振动安全性检验提供了数值依据。

1 模态分析

1.1 模态分析简介

模态分析是分析系统机构的各阶固有频率和振型［4］。系统受外界激励做强迫振动时，若外界激励的频率接近于系统的固有频率，强迫振动的振幅可能会过大，并引起机械和结构较大的变形和动应力，这种现象叫作共振。一个系统有多个固有频率，一般情况下只需研究低阶的系统频率，因在这些低阶的频率上较易引起振动并发生共振，而在其他频率上振动则较为困难。若引起系统振动的频率成份较复杂，系统一般会再最容易引起共振的频率上振动，而将其他频率过滤掉。因此在设计及实际生产过程中必须要避免共振现象的发生。对于天线座组件［5］，其振动可表示为系统各阶固有振型的线性组合，其中低阶固有振型对结构振型的影响更大，同时对机构的动态特性也起决定性作用。

模态分析有两种方法［6］:基于有限元建模的理论模态分析和基于系统传递函数测试的试验模态分析。随着有限元技术的发展及产品开发周期的要求，有限元模态分析越来越多地应用于产品开发设计中，在设计阶段就能掌握并及时修改产品的固有特性。试验模态分析则可验证系统所达到的固有特性，同时验证了有限元建模的合理性，对以后的有限元模态预估分析提供建模经验且具有指导作用。

1.2 模态分析求解原理

模态分析是用来确定结构振动特性的一种技术［7］，其可确定结构的固有频率和振型及模态参数。对于一个有n 个自由度的振动系统，需用n 个独立的物理坐标来描述其物理参数模型。在线性范围内，物理坐标系的自由振动响应为n 个主振动的线性叠加。每个主振动均是一种特定形态的自由振动，振动频率即为系统的主频率，振动形态即为系统的主振型，根据达朗贝尔原理可推得动力平衡方程为

其中，F 为激励向量;X 为响应向量;M、C、K 分别为质量矩阵、阻尼矩阵、刚度矩阵。

对式(1)作拉氏变换得

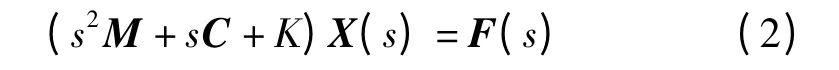
用jω 替代s，进入傅氏域内处理

对于线性不变系统，系统的任意一点的响应均可表示成各阶模态响应的线性组合

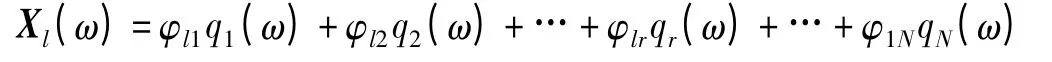
式中，qr(ω)为r 阶模态坐标;φlr为l 测点的r 阶模态振型系数。对于N 个测点，各阶振型系数可组成列向量，称为r 阶模态振型φr={φ1r，φ2r，…，φNr}T;各阶模态向量组成模态矩阵φ=［φ1，φ2，…，φN］T，物理意义:各阶模态对响应的贡献量。Q=［q1(ω)，q2(ω)，…，qN(ω)］T为模态坐标。

根据式(3)可得到无阻尼下系统的固有频率方程为

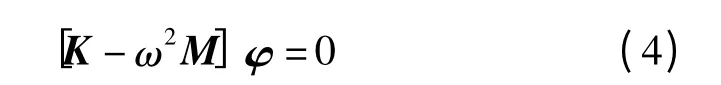
解此方程可对应得到系统的特征值和特征向量，以及对应于系统的频率和振型。

2 天线座转台的有限元分析

2.1 天线座转台的3D 模型和有限元离散

由于天线座转台的结构较为复杂，而建模的好坏直接影响到有限元分析的结果，因此可利用三维软件UG 来建立三维模型。在三维建模时，简化了小的让位台阶和过渡圆角，是加工工艺和装配工艺的需要，其对结构力学性能基本无影响，因此可删除这些结构特征。建立好的模型如图1 所示。

图1 某雷达转台的三维模型

2.2 天线座转台的有限元离散

有限元法(Finite Element Method，FEM)是一种获得工程问题近似解的数值计算方法［8］，其理论基础是将连续结构体划分为有限大小，彼此只在有限个节点(Nodes)相连接，有限个单元(Elements)的组合体来研究，即将一个离散结构作为实际连续结构的近似力学模型，并在离散结构上进行数值计算分析的方法。因实际的工程结构多数均为复杂的结构形式，有时无法用经典的弹性力学通过求解微分方程得到其解析解。而有限元方法则避免了求解微分方程，因此有限元法可求解复杂形状、结构、复杂边界条件的工程问题，使得有限元法分析及优化技术在现代设计中起着重要作用。

在UG 中建好模型后进入高级仿真模块。UG 结构分析模块支持4 节点和10 节点四面体单元，文中选取10 节点四面体单元，并根据单元尺寸自动设定功能推荐值设置全局单元尺寸为8.9，该值是控制整个实体上四面体单元边缘长度的参数。UG 支持3 种三维网格划分运算法则，即Facet、Parametric 和Sequence，其中Facet 算法是一种灵活的网格生成法则，对于大多数几何体均可生成高质量的网格;在Facet 算法生成网格失败时可使用Parametric 算法进行尝试;而Sequence 算法是上述两种算法的综合应用，该方法首先尝试使用Facet 算法生成网格，一旦失败则自动启动Parametric 算法进行网格划分。一般均选择Sequence算法生成网格。UG 中有3 种方法控制10 节点单元中节点到几何体的映射，即Mixed、Curved 和Linear 方法。Mixed 方法将雅可比值小于临界值的单元中节点映射到几何体;Curved 方法将所有中接点均映射到几何体，而不顾及其对单元质量的影响;Linear 方法将所有中节点都映射到两点间的直线上。使用Mixed 方法以控制单元质量。进行网格划分，划分网格后有限元模型的节点数为51 229，单元数25 861，有限元模型如图2 所示。

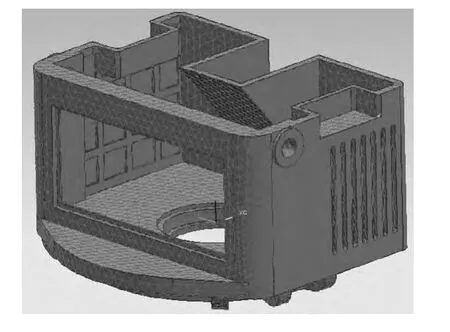
图2 转台的有限元网格模型

2.3 材料属性及分析的边界条件

创建固定约束［9］，固定约束是对节点的一种约束，即将某节点的依赖自由度定义为其他若干节点独立自由度的固定。常用于表征一些特定的物理现象，比如刚性连接等，固定约束也可用于不相容单元间的载荷传递。在天线座的底部连接部分创建固定约束的边界条件，将圆周上节点的约束定义圆心点的约束边界条件，约束完整模型。并分别在天线铰接孔处向下施加25 000 N的载荷。对模型设置材料属性，选择铝作为加工材料，弹性模量E=70 GPa，密度为2 800 kg/m3，泊松比为0.3。在UG 软件中可获得转台的质量为128.1 kg。UG 分析中采用求解无阻尼自由振动的实特征值求解序列(Semodes 103)。

2.4 模态计算结果分析

表1 和图3 ～图6 显示了该天线座转台前8 阶固有频率和前4 阶固有频率与振型。

表1 模态仿真结果

低阶模态对结构响应贡献较大，因此列举前4 阶模态基本可以反映天线座转台的动态特性。

图3 1 阶时模态

图4 2 阶时模态

图5 3 阶时模态

图6 4 阶时模态

图7 应力云图

在应力分析中，最大应力集中和变形出现在前安装面板孔的尖角上，因此在天线座的设计中，特别注意在尖角处的位置通过采用倒圆［10］，倒角方式，有效地改善了其力学性能。模型的建立对有限元分析的结果有着重要影响，模型精度可以决定有限元分析的成败，网格划分的粗细对精度的影响也尤为重要。

3 结束语

(1)用UG/NX 和NX Nastran 软件能精确地模拟和分析实际工程中的模态问题。(2)获得了天线座转台的模态分析结果，从而为天线座转台的动力学特性的修改和优化指出了方向。(3)计算结果表明，此天线座转台的固有频率满足性能的要求。

通过观察谐振峰值点所对应的结构系统的响应，预测结构系统的持续动力特性，从而验证结构设计能否成功地克服共振、疲劳及其他受迫振动引起的有害影响。鉴于天线座在雷达通讯系统中的重要性，所以在天线座设计开发过程中，有必要对各种方案进行分析和考虑。通过有限元分析的方法，借助NX Nastran和UG 软件对天线座结构进行模态分析，不仅可缩短雷达系统开发时间，结合天线座模态分析又可以保证与整个雷达总体系统模态匹配，确保达到结构设计要求。

［1］ 吴凤高.天线座结构设计［M］.西安:西北电讯工程学院出版社，1986.

［2］ 孔小进.某全向天线座的结构设计［J］.舰船电子对抗，2006，29(1):62－64.

［3］ 李龙.某天线座的模态及应力分析［J］.电子机械工程，2009(2):62－64.

［4］ 徐稀文，平雪良，陈鲁刚，等.弧焊机器人大臂结构模态分析［J］.机械设计与制造，2012(6):151－153.

［5］ 陈云飞，刘维明.天线座固有频率的计算分析［J］.无线电工程，1997，27(3):39－42.

［6］ 张小安，张艳.天线座结构的试验模态与理论模态的分析比较［J］.电子机械工程，2005，21(1):37－40.

［7］ 管迪华.模态分析技术［M］.北京:清华大学出版社，1995.

［8］ 叶尚辉.建立有限元模型的一般方法［J］.电子机械工程，1999(6):17－21.

［9］ 周焕林，胡宗军.MSC.Nastran 入门与实例［M］.合肥:合肥工业大学出版社，2005.

［10］杜平安.结构有限元分析的形状处理方法［J］.机械与电子，2000(1):26－27.