基于DOA估计的RLS-CMA算法
(中国人民解放军92512部队,浙江宁波315000)
0 引言
在移动通信系统中,同信道干扰和频谱资源拥挤已经成为人们关注的重要问题之一。同信道干扰来源于频率的复用,由于地理和环境的因素,同信道干扰是造成信道损失的主要原因。近几年来,阵列天线的同信道的盲处理技术,引起了人们的关注。最早利用信号的恒模特性的自适应数字滤波器算法是在1980年[1],该方法是用在除了信号具有恒定包络以外先验知识未知的盲自适应波束形成器,Godard[1]利用最小恒模代价函数,得到了与Wiener在最小均方误差(MSE)准则下半盲估计的近似解。
尽管恒模算法具有很多优点,但由于CMA收敛速度较慢,不能很好地应用在动态环境中[2]。在强干扰的环境中,恒模算法不能很好地恢复期望信号[3],在实际的无线环境中,随着用户的激增,通信环境日趋恶劣,这就要求波束形成算法在强干扰的环境中,仍然能够快速而准确地收敛于期望信号。文献[4]的作者提出的MESB-CMA算法就是基于这方面的考虑。但MESB算法因为涉及矩阵求逆,计算量较大。而LMS算法虽然不涉及矩阵求逆,对阵列幅相差也不敏感,但其收敛速度较慢。考虑到RLS[5-6]算法具有LMS算法的优点,并且收敛速度要比LMS算法提高一个数量级[7-8],平稳环境下在每个采样瞬间计算的权值都是最好的选择(基于对接收数据的最小二乘方法),本文提出RLS-CMA算法:是在级联的恒模阵列与自适应干扰对消器中,把RLS和CMA结合起来,充分发挥二者优点,弥补其不足,由RLS算法决定CM阵列的初始权,同时通过对权向量多项式求根[9]获得下一级的初始权向量,由CMA方法更新权向量,利用这种方法,算法的稳健性以及捕获能力进一步提高。
本文的目的是,通过恒模阵列(CM)来分析RLS-CMA算法以及相对应的恒模(CM)阵列的稳态特性与可靠性。可靠性是指在一定环境条件下收敛性能。当干扰信号强于期望信号时,该算法仍能捕获到期望信号而不是跟踪功率较大的干扰信号,并且算法对阵列幅相差不敏感。
1 阵列建模与RLS-CMA算法提出
1.1 CM阵列与信号模型
如图1所示,恒模阵列,假设有L个源信号入射到具有M个阵元的均匀线阵(ULA)上。阵列的输出信号向量X(k)构成了恒模阵列的输入信号向量。
阵列第m个阵元的输出信号可以表示为

式中,{s i(t)}(i=1,…,L)为信源信号,n m(t)为加性高斯白噪声。在假设窄带信源的条件下,φi=2π(d/λ)sin(θi),d为阵元间距,λ为信源的波长,θi为第i个信源的波达方向。
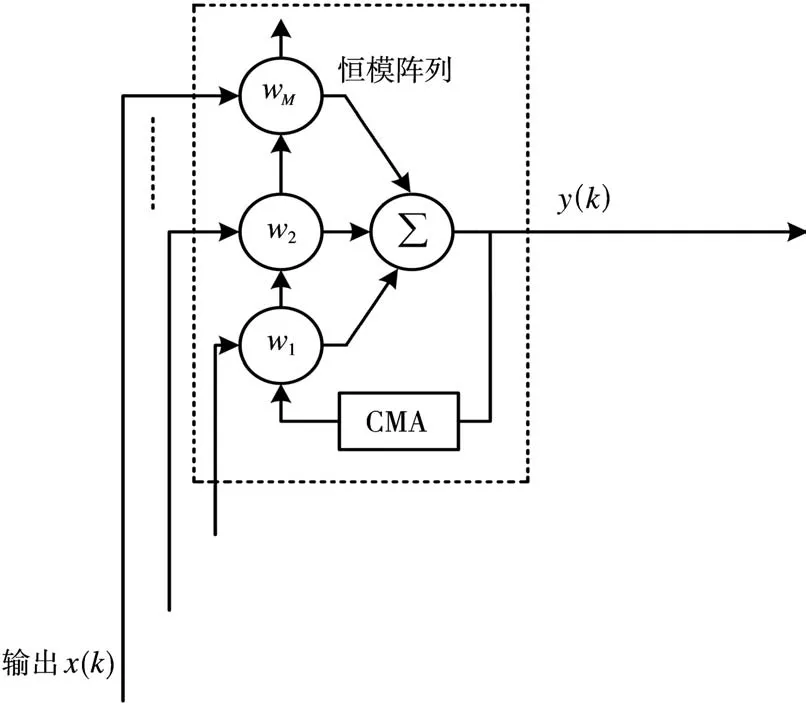
图1 恒模阵列系统的框图
经过采样后的阵列信号用矩阵形式表示,这样定义,X(k)=e1(k),有
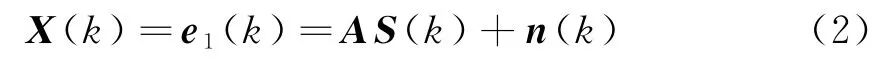
式中,

通常对等距线阵感兴趣,但是恒模阵列的信号恢复性能却与阵列的几何结构无关[7]。矩阵A可以是任意矩阵。
接收数据向量X(k)的自相关矩阵R x=E{X(k)XH(k)},由下式给出:

式中,R s=E{S(k)SH(k)}和R n=E{n(k)nH(k)},假定S(k)与n(k)互不相关,且均值为零,所以R s,R n可以用对角矩阵∑s,∑n表示:

式中,∑s相应的对角元素。
实际计算R时,用其由K次采样信号得到的估计值代替。
1.2 RLS-CMA算法
1.2.1 RLS算法
这里直接给出最小二乘(RLS)准则,为

式中,

称为先验估计误差;
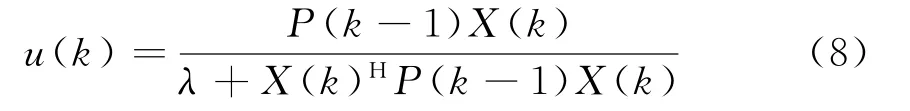
称为增益向量,其中

0<λ<1称作遗忘因子。
对于恒模信号,恒模阵列捕获信号的性能与初始权向量和阵列输出端的相对信号功率有关。为提高CMA算法的稳健性,本文用式(6)RLS算法[6]迭代产生初始权向量。
1.2.2 权向量多项式求根法
基于文献[9]提出的波束形成算法对一个用户实现波束形成后,从算法的权向量多项式中可以求出其他用户的波达角的结论时并没有用到用户信号是恒模信号的条件,所以不仅仅针对恒模信号,对其他信号应该同样适用。因此,本章大胆把该结论应用于RLS算法中,与恒模算法相结合,以实现对多个信号的分离接收。下面的推导和仿真证明是可行的。
设递推最小二乘算法收敛于某一信号,这里不妨设算法收敛于信号s k,所以有TX,将展开,关于s1对^s k=WTX求内积得

由假设知各信号之间是相互独立,且假设算法收敛于信号s k,故有

依次关于s2,…,s p对TX求内积,只有关于s k求内积时得到

其余内积均为零,并得到类似的方程,联立这些方程得

令e-jφi=x i,从式(13)的前p-1个方程组可以得到权向量方程w1+w2x+w m x m-1=0。可以看到当算法收敛于某一信号s k后,p-1个含有其他来波方向的函数e-jφi(i=1,…,p,i≠k)是以波束形成算法的权向量的各分量为系数的一元M-1次方程的解。这样便盲估计出矩阵。为了回避匹配搜索所带来的运算量,应用类似ESPRIT的方法[9]。设为第i个信源阵列流形估计的两部分,有,其中d是天线阵列两部分之间的距离,可得
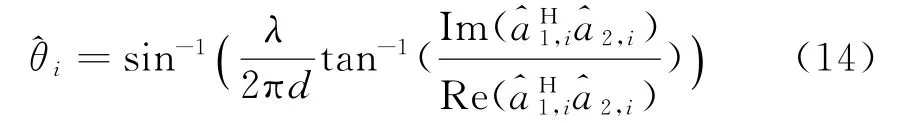
至此已推导出权向量多项式求根方法,不需要进行复杂的谱峰搜索,所需采样点数较少,所以计算量较小。并且在对其中一个信号收敛后,即可并行对其他多路信号进行估计,从而作为下一级恒模阵列的初始权向量。使整个算法实现起来比较简单,收敛迅速且不需要信号对消。
从数学角度分析,一个任意的一元m-1次方程的解不一定存在;但是从波束形成的物理意义而言,如果有多个用户信号同时被天线阵接收,由上述推导可知,当算法对任一用户形成波束后,必然要在其他用户方向上产生零陷。因此从物理意义上讲,权向量多项式一定有解。在本算法的实施过程中,还有一个如何对待“虚解”的问题[9]。因为当信号数小于阵元数时,求解权向量方程时,会产生异于用户方向函数的“虚解”。事实上,当把从“虚解”中算出的方向作为期待信号的来波方向时,由于在该方向上并没有用户信号存在,按照初始权向量的赋值没有对任何用户信号产生初始增益,但是经过最小二乘恒模算法的多次迭代修正后,仍然会收敛于某一其他用户信号,这时对其权向量方程求解,获得的其他用户的波达方向也可以验证这一点,从而反馈出此解为“虚解”的信息。如果充分利用求解权向量方程反馈出的解的信息,就可避免错误获得虚解方向的问题。
2 RLS-CMA稳态特性分析
2.1 恒模阵列维纳权
假设恒模阵列捕获到第i个信号,则误差信号e i(k)=s i(k)-y i(k),根据均方估计理论,权向量收敛时,估计误差与数据正交,即E[X(k)e∗i(k)]=0。均方误差为

对式(15)求偏导并令其为零,据最小均方误差(M MSE)准则,得
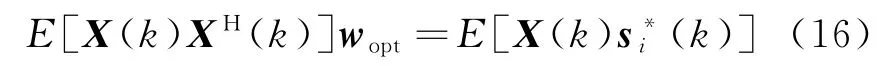
或写作

式中,R x=E[X(k)XH(k)],p i=E[s∗i(k)X(k)]。将式(2)代入式(17),得

式中,a i为导向矢量的第i列,即为第i个信源的导向矢量。则恒模阵列的输出功率为

由于ξmin≥0,

也就是说,恒模阵列的输出信号功率收敛于被捕获到的第i个信号的功率。
2.2 输出SINR与SNR
在文献[10]中,输出信号干扰噪声比(SINR)与移位因子βi,j[11]有关,假设捕获到第i个信号源,则输出信干噪比(SINR)为
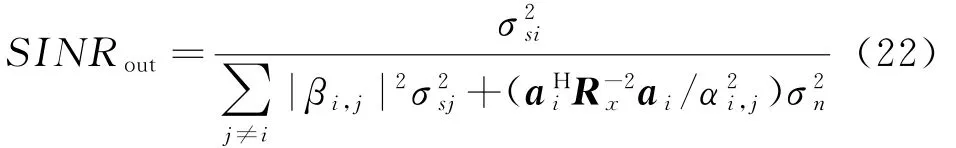
可以看出,当两个恒模信源靠得较近时,阵列输出SINR下降。当我们不考虑同信道干扰时,也就是说,得到的输出信噪比(SNR)为
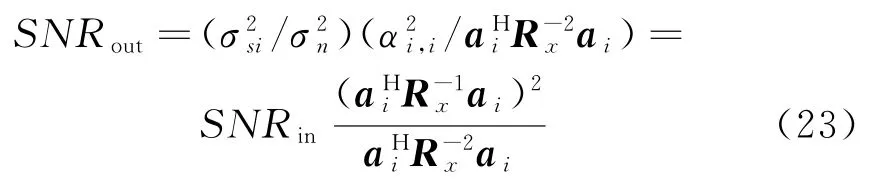
可以证明,SINRout≤SNRout≤M·SNRin,见文献[10]。 也就是说,当信号源距离较远时,SINRout≈SNRout。
3 计算机实验仿真
为验证本文算法的性能,在计算机上进行了仿真。
在9元ULA阵列中,d/λ=0.5,期望信号分别从100°,40°入射到该阵列上,其信噪比(SNR)分别为0 dB和20 d B。干扰信号的波达方向为150°,干扰信号的INR为35 dB。期望信号与干扰均为恒模信号。为比较,我们先仿真了未用RLS算法产生的权当作初始权的情况,如图2所示,由于恒模特性错误收敛至大功率的150°强干扰信号,而在期望信号的100°,40°方向形成零陷。在其后应用RLS算法后,如图3和图4所示,利用RLSCMA算法可以在第一级中捕获到波达方向为100°信号,在第二级中是方向为40°信噪比较大的信号。可以看到,对应不同的权值,分别在100°,40°的信号方向形成了良好的主瓣,并且150°方向一直是保持比较深的零陷,即在强干扰情况下对期望信号做到了良好的分离接收。
仿真实验同时计算权值迭代过程中接收信号的输出SINR,可以观察到该算法稳健性较好,在20次迭代内已很好地收敛。并且权矢量收敛后,每个波束形成输出分别锁定不同的信号,充分说明该算法具有良好的收敛速度及鲁棒性。
图5给出了信号存在幅相差时的输出SINR(幅度差≤2 dB,相位差≤15°)。可以看到相位差和幅度差对算法的性能影响不大,该算法在幅相差不是很大的情况下仍可以较好地恢复恒模信号。
在这里有必要说明的是,权向量初值取W(0)=a(θ0)的基于线性约束的最小二乘恒模,即LC-LSCMA,在干扰信号强于期望信号15 dB左右以内时,能收敛到弱期望信号,但在强干扰下算法无法收敛到小期望信号。而本文提出的算法,在干扰信号强于期望信号35 dB时依然有效。
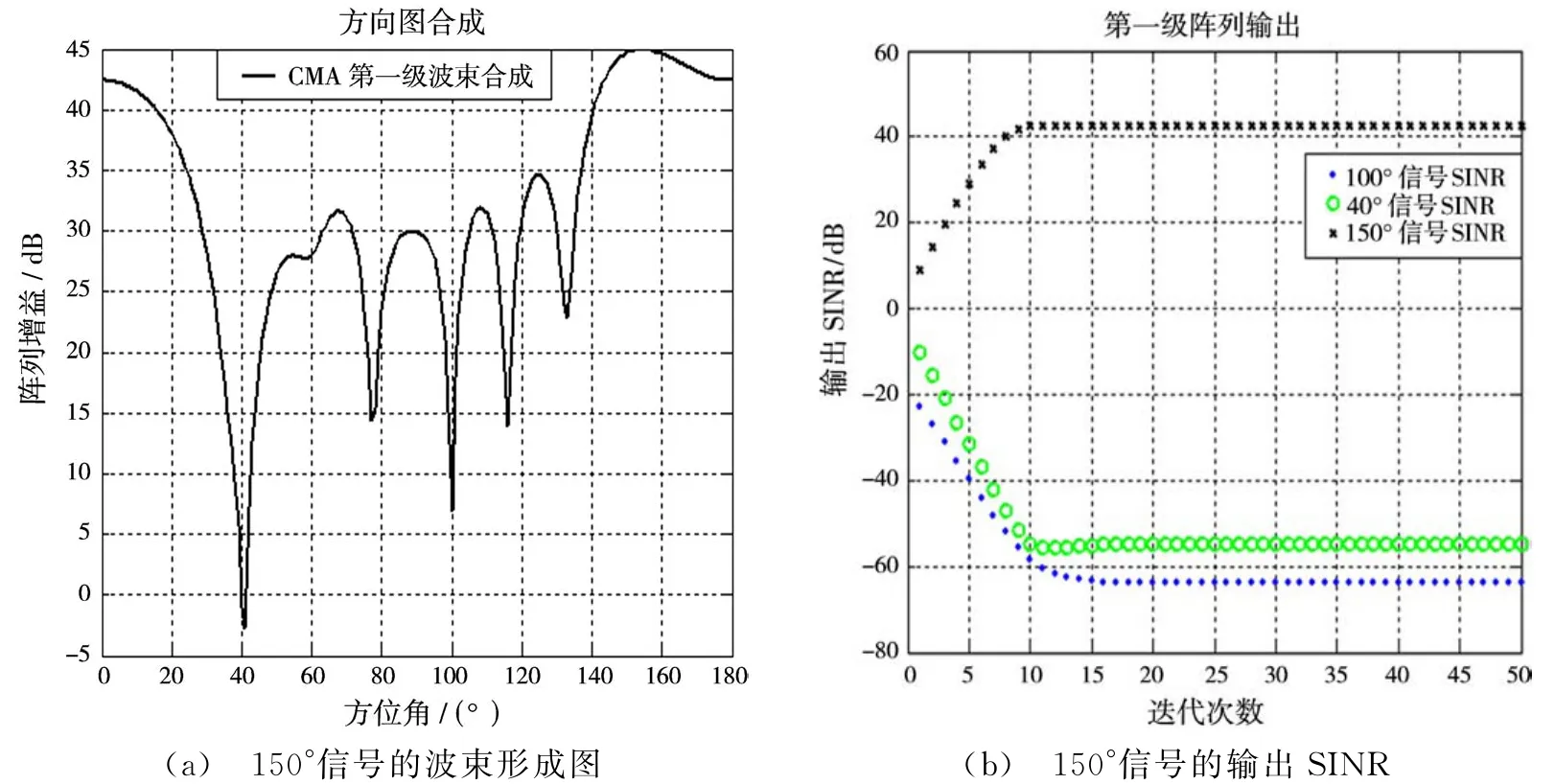
图2 150°信号的波束形成图和输出SINR
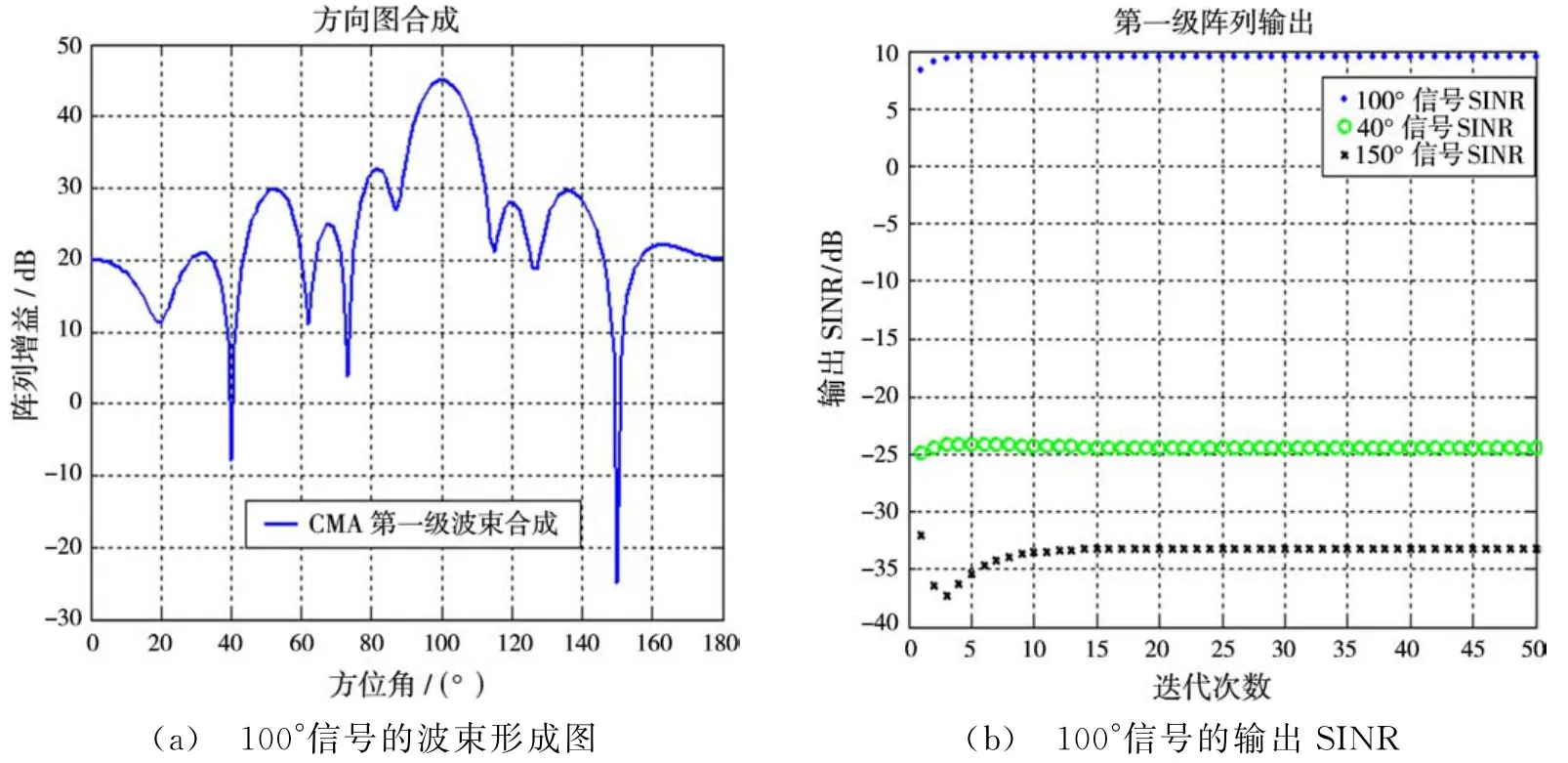
图3 100°信号的波束形成图和输出SINR

图4 40°信号的波束形成图和输出SINR

图5 幅相差对输出SINR的影响
4 结束语
本算法将RLS算法与恒模相结合,通过用RLS算法产生初始权,继而通过对权向量多项式求根获得下一级的初始全向量,推导出一种RLSCMA方法。此方法:(1)在不需要进行正交化和多级对消情况下,解决了CMA多波束形成过程中对同一目标的重复收敛问题;(2)以较少的迭代次数、较小的计算量迅速收敛至不同期望权向量,对多路信号进行了良好的盲分离;(3)通过应用RLS算法产生初始权,在强干扰情况下对期望信号做到了良好的分离接收,提高了期望信号的输出SINR。
但是因为要对权向量多项式求根,所以运算量有所增加;而且当实际系统中出现相关干扰时,此时该算法不能正常工作,必须进行修正。所以相关干扰环境下的多用户分离问题还需要进一步研究。
[1]GODARD D N.Self-Recovering Equalization and Carrier Tracking in Two-Dimensional Data Communication Systems[J].IEEE Trans on Communications,1980,28(11):1867-1875.
[2]GOOH R P,LUNDELL J D.The CM Array:An Adaptive Beamformer for Constant Modulus Signals[C]∥IEEE International Conference on Acoustics,Speech,and Signal Processing,Tokyo,Japan:[s.n.],1986:2523-2526.
[3]AGEE B G.The Least-Squares CMA:A New Technique for Rapid Correction of Constant Modulus Signals[C]∥IEEE International Conference on Acoustics,Speech,and Signal Processing,Tokyo,Japan:[s.n.],1986:953-956.
[4]王红梅,徐宝坤.基于MESB-CMA联合自适应算法的性能分析[J].雷达科学与技术,2007,5(5):384-389.WANG Hong-mei,XU Bao-kun.Performance Analysis of MESB-CMA United Adaptive Algorithm[J].Radar Science and Technology,2007,5(5):384-389.(in Chinese)
[5]张贤达,保铮.通信信号处理[M].北京:国防工业出版社,2002:309-310.
[6]何振亚.自适应信号处理[M].北京:科学出版社,2002:68-76.
[7]张贤达.现代信号处理[M].北京:清华大学出版社,2002:206-211.
[8]许家安.自适应波束形成算法及外辐射源雷达威力分析[D].南京:南京理工大学,2005.
[9]郭艳.恒模算法及其在盲波束形成中的应用[D].西安:西安电子科技大学,2002.
[10]SHYNK J J,GOOCH R P.The Constant Modulus Array for Cochannel Signal Copy and Direction Finding[J].IEEE Trans on Signal Processing,1996,44(3):652-660.
[11]SHYNK J J,KEERTHI A V,MATHUR A.Steady-State Analysis of the Multistage Constant Modulus Array[J].IEEE Trans on Signal Processing,1996,44(4):948-962.

