基于四元数的极化敏感阵列波束形成

(电子科技大学电子工程学院,四川成都611731)

0 引言

极化敏感阵列又被称为矢量阵列,它可以获取空间电磁信号的极化信息,因而具有比传统标量阵列更优越的系统性能[1]。近年来,极化敏感阵列自适应波束形成吸引了大批学者的关注,它可以同时利用期望信号和干扰信号在空域和极化域中的特征差异,实现极化域-空域联合的自适应波束形成。文献[2]分析了完全极化情形下极化敏感阵列的滤波性能;文献[3]讨论了参数估计误差对极化滤波性能的影响。现如今常见的针对极化敏感阵列的信号处理大多是基于复数的长矢量方法,它将极化敏感阵列所有分量的输出数据排列成一个长矢量,破坏了阵元各分量输出信号之间固有的正交特性,这也在一定程度上降低了极化敏感阵列的优越性能。作为复数在四维空间上的直接扩展,四元数已经成为了多维信号处理的一个重要工具[4]。四元数的正交结构能够很好地保持矢量阵元各分量之间的正交特性,因而得到了广泛的应用。现有的基于四元数信号模型的极化敏感阵列信号处理主要在信号波达方向和极化参数估计方面,对其在滤波方面的讨论甚少。文献[5]提出了基于四元数的MUSIC算法,文献[6]提出了双四元数的方法用于MUSIC参数估计。文献[7]在文献[5]的基础上给出了一种降维的四元数MUSIC算法,它们都具有比传统的长矢量方法更优的参数估计性能。在波束形成方面,文献[8]讨论了四元数复数形式的最小均方算法,文献[9]基于四元数的信号模型提出了四元数最小方差无失真响应(Q-MVDR)算法,它们都获得了良好的滤波性能。本文基于文献[9]的思想,将最大信号干扰噪声比准则应用于四元数极化敏感阵列滤波,求得了四元数最优权向量并通过计算机仿真验证了文中方法的正确性。

1 四元数信号模型

1.1 四元数

四元数可以看作是复数在四维空间上的直接扩展,我们常用的是Hamilton四元数。一个四元数q由四个分量组成(一个实部和三个虚部),可以表示为

式中,i,j,k都是虚部单位,a,b,c,d为实数,且满足

四元数具有许多特性[10-11],大多数复数的性质可以直接扩展到四元数,但是四元数乘法不满足交换律,对于两个四元数q1,q2有

下面列出一些常用的四元数的性质：

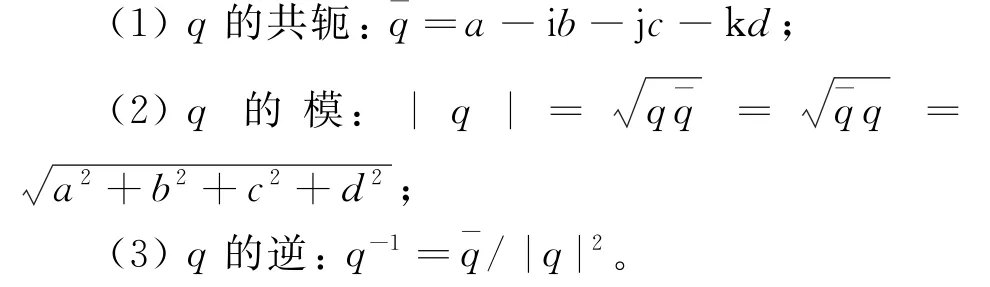
一个四元数q可以唯一地表示成两个复数的形式：

式中,q1,q2是两个复数且q1=a+jc,q2=b+jd。本文后面将用四元数的这种分解形式来表示四元数信号模型。

1.2 四元数信号模型

极化敏感阵列由相互正交的M个电偶极子对构成,阵列结构如图1所示,两个正交的电偶极子分别沿x轴和y轴方向放置,可以分别接收来自x方向和y方向的电场分量。各个阵元沿y轴排列构成均匀线阵,阵元间距为d,这种阵列形式也被称为两分量阵列。

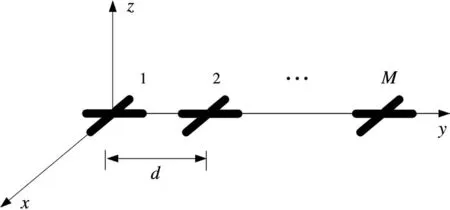
图1 极化敏感阵列示意图

假设空间有一个远场窄带信号入射到阵列上,信号的复包络为s(t),入射俯仰角为θ,方位角为φ,入射信号为完全极化的电磁波,且极化相角和极化相位差分别为γ,η,选取第一个阵元为相位参考阵元则第m个阵元接收到的信号的两个分量x m1(t),x m2(t)可以表示为

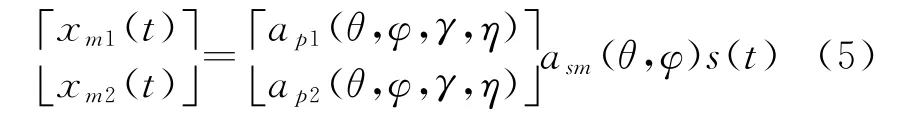
式中,a sm(θ,φ)为由第m个阵元相对参考阵元的空间相位差引起的,a p1(θ,φ,γ,η),a p2(θ,φ,γ,η)分别为两分量阵列的极化导向矢量,且有

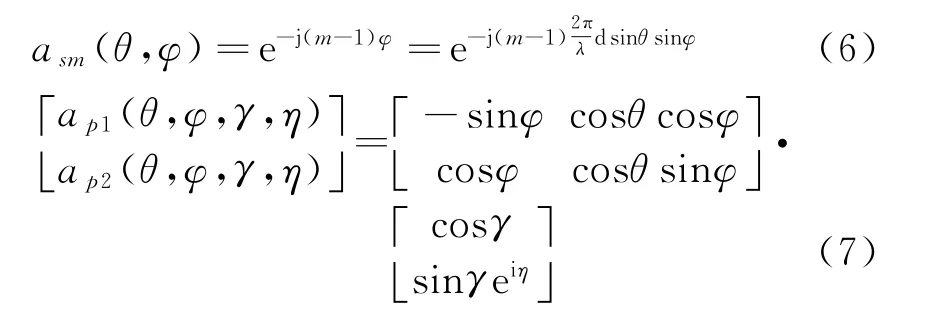
为了保持各阵元输出信号之间固有的正交特性,构造四元数信号模型,把两分量阵列输出复数形式的两路信号通过以下方式组合为一路信号：

式中,P(θ,φ,γ,η)为四元数形式的极化导向矢量。把四元数形式的信号模型推广到阵列上,可得M元阵列的接收信号：

式中,a s(θ,φ)=[1,e-jφ,…,e-j(M-1)φ]T为阵列的空间导向矢量[12]。当空间有K个信号入射且考虑高斯白噪声的影响：

式中 ,d k=P k(θ,φ,γ,η)a sk(θ,φ)为四元数形式的极化域-空域联合导向矢量;N(t)=N1(t)+iN2(t)为四元数形式的高斯白噪声,其中N1(t)为x分量的复白噪声矢量,N2(t)为y分量的复白噪声矢量。

2 基于四元数的极化阵列波束形成

假设空间有一个期望信号和与之不相关的干扰信号入射,期望信号s1(t)波达角为(θ1,φ1),极化参量为(γ1,η1);干扰信号s2(t)波达角和极化参量分别为(θ2,φ2),(γ2,η2),则阵列接收信号的四元数模型表示为

阵列滤波后的输出信号y(t)为接收信号矢量X(t)的四元数加权求和,即

式中,w为M维的四元数加权矢量,符号{◁}表示四元数共轭转置。为了获得较好的滤波性能,采用最大信号干扰噪声比(SINR)准则来求得最优权矢量。输出信干噪比为

Rs和Rin分别为期望信号和干扰加噪声的四元数协方差矩阵,Ps为期望信号的功率。又因为期望信号和干扰不相关可得输入信号的四元数协方差矩阵为

可见,在入射信号确定的环境下,输出SINR仅是权矢量w的函数,为了求得w的最优解使输出SINR最大,采用与复数最优权矢量相类似的推导方法。将干扰加噪声协方差矩阵Rin进行分解Rin=R1/2inR1/2in,然后将问题转化为求四元数Hermitian矩阵的最大特征值对应的特征向量即为最优权矢量。利用四元数梯度操作及运算法则[13]可以解得四元数最优权矢量的表达式为

可见基于最大信干噪比准则的最优权矢量需要根据干扰加噪声协方差矩阵Rin求得,根据矩阵求逆引理可得

可以证明如下：

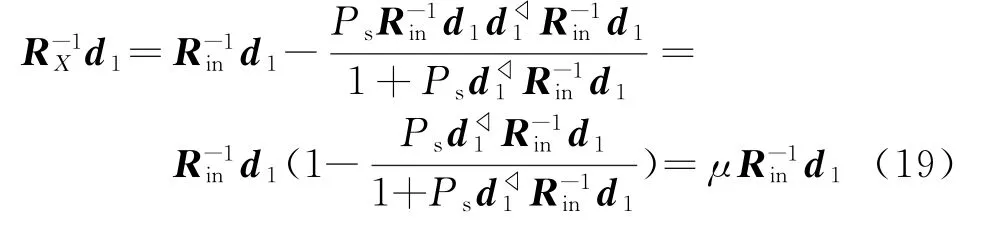
3 仿真分析

为了验证基于四元数的极化敏感阵列的滤波性能,将其与传统的长矢量滤波方法进行对比。

(1)采用8阵元均匀线阵,阵元间d=λ/2,为了简化分析假设所有信号入射方位角φ=90°,期望 信号入射俯仰角θ1=30°,极化参量(γ1,η1)=(10°,90°),SNR=5d B,干扰信号极化相位差η2=90°,INR=20 dB,当干扰入射角度θ2从0°到60°变化时,图2给出了不同的干扰极化相角γ2与输出SINR的关系。

图2 干扰角度和极化参量对SINR的影响

从图2可以看出,四元数滤波方法与长矢量方法具有相近的滤波性能。当干扰信号到达角与期望信号间距很大Δθ≥10°时,利用空域滤波就能达到很好的滤波效果,极化参量影响不大;当干扰信号到达角与期望信号角度相近Δθ＜10°时,空域滤波失效这时可以利用极化差异来完成滤波;特别当γ2=90°时即使干扰信号从期望信号方向入射,即θ2=30°也能很好的滤波;只有当干扰信号到达角和极化参量与期望信号参量完全一致时(θ2=30°,γ2=10°)滤波性能严重下降,此时算法失效。

考虑四元数方法与长矢量方法滤波的计算量,从自相关矩阵R X的估计^R X入手,参考文献[5]的分析方法可得一次采样快拍下四元数方法需要4M2个实数存储单元,而长矢量方法需要8M2个实数存储单元。对于N次快拍四元数方法最后需要4N2次实数除法,而长矢量方法需要8N2次实数除法。由此可见,与长矢量方法相比在相同的滤波性能下,四元数滤波方法减少了一半的数据存储量和除法运算量,这样可以加快数据处理速度以满足实时性的要求。

(2)图3给出了四元数方法和长矢量方法输出SINR随阵列指向误差的影响。期望信号入射俯仰角θ1=20°,极化参量(γ1,η1)=(30°,90°),SNR=15 dB,干扰信号入射俯仰角θ2=50°,极化参量(γ2,η2)=(60°,90°),INR=20 dB,指向误差为-8°～8°。从图中可以看出四元数方法受指向误差的影响程度要低于长矢量的方法,这是因为四元数的四维超复数正交结构保持了阵元各分量之间固有的正交特性,提高了阵列对指向误差的稳健特性。

图3 指向误差对输出SINR的影响

4 结束语

本文基于四元数信号模型将最大信号干扰噪声比准则应用于波束形成获得了四元数最优权向量,完成了极化敏感阵列的滤波。基于四元数的方法保持了阵元各分量之间固有的正交特性,当阵列存在指向误差时,具有比传统复数长矢量方法更好的稳健特性。计算机仿真验证了文中方法的正确性。

[1]庄钊文.极化敏感阵列信号处理[M].北京：国防工业出版社,2006：30-80.

[2]徐振海,王雪松,肖顺平,等.极化敏感阵列滤波性能分析：完全极化情形[J].电子学报,2004,32(8)：1310-1313.XU Zhen-hai,WANG Xue-song,XIAO Shun-ping,et al.Filtering Performance of Polarization Sensitive Array：Completely Polarized Case[J].Acta Electronica Sinica,2004,32(8)：1310-1313.(in Chinese)

[3]章力强,陈信,李相平,等.参数估计误差对极化滤波性能影响分析[J].雷达科学与技术,2012,10(2)：198-202.ZHANG Li-qiang,CHEN Xin,LI Xiang-ping,et al.Impact of Parameter Estimate Error on Polarization Filtering Performance[J].Radar Science and Technology,2012,10(2)：198-202.(in Chinese)

[4]BÜLOW T,SOMMER G.Hypercomplex Signals-A Novel Extension of the Analytic Signal to the Multidimensional Case[J].IEEE Trans on Signal Processing,2001,49(11)：2844-2852.

[5]MIRON S,LE BIHAN N,MARS J I.Quaternion-MUSIC for Vector-Sensor Array Processing[J].IEEE Trans on Signal Processing,2006,54(4)：1218-1229.

[6]LE BIHAN N,MIRON S,MARS J I.MUSIC Algorithm for Vector-Sensors Array Using Biquaternions[J].IEEE Trans on Signal Processing,2007,55(9)：4523-4533.

[7]李京书,陶建武.信号DOA和极化信息联合估计的降维四元数MUSIC方法[J].电子与信息学报,2011,33(1)：106-111.

[8]常文秀,陶建武.四元数复数形式的最小均方算法[J].信号处理,2011,27(10)：1515-1519.

[9]TAO Jian-wu,CHANG Wen-xiu.The MVDR Beamformer Based on Hypercomplex Processes[C]∥2012 IEEE International Conference on Computer Science and Electronic Engineering,Hangzhou,China：[s.n.],2012：273-277.

[10]HAMILTON W R.On Quaternions[M].Royal Irish Academy,1843.

[11]TOOK C C,MANDIC D P.A Quaternion Widely Linear Adaptive Filter[J].IEEE Trans on Signal Processing,2010,58(8)：4427-4431.

[12]何子述,夏威.现代数字信号处理及其应用[M].北京：清华大学出版社,2010：301-310.

[13]MANDIC D P,JAHANCHAHI C,TOOK C C.A Quaternion Gradient Operator and Its Applications[J].IEEE Signal Processing Letters,2011,18(1)：47-50.