基于多尺度几何分析的SAR图像融合

(电子科技大学电子工程学院,四川成都611731)

0 引言

穿墙雷达成像技术由于其能够检测识别建筑物内目标,一直是热门的研究领域[1]。在实际应用中,穿墙雷达成像技术分成两个领域,即穿墙目标检测与识别[2-3]和建筑布局成像技术[4-6]。

建筑布局成像技术在实际应用中有诸多好处,近年来逐渐引起国内外学者的研究兴趣。第一,建筑布局成像在穿墙目标成像中能够为目标的相对位置提供正确的参照物;第二,建筑布局成像能够为多径虚假目标的提取和抑制提供可能性,并且可依此估算出成像目标位置和实际目标位置的相对偏移;第三,建筑布局成像结果中的目标和孤立墙体的相对位置对孤立墙体的强度补偿具有重要作用;最后,建筑布局成像为人员进入建筑物内部提供合适的方向和路径。

由于在不同视角下对同一场景进行成像,丰富了场景图像信息,因此目前一般采用对多幅单视角图像进行融合,从而形成一幅信息更丰富、对比度更高、信噪比更大的全景图像。现今采用的图像融合方法一般是针对不同模式下的两幅图像,如光学图像和红外图像、SAR图像和光学图像、SAR图像和全色图像[7-9]。但对两幅相同模式下的图像融合却少有研究,而穿墙雷达多通道多视角的图像融合就属于此类。另外,由于透视探测场景成像中室内和杂波的散射特征不同于其他机制的雷达图像,因此一些基于杂波统计特征的图像融合方法不适用于此[10]。

目前,穿墙雷达图像融合技术主要围绕单尺度域下进行[11-15],但图像不同层次的细节和边缘信息却是反映在图像的不同尺度上,单一尺度的图像融合技术并不能完全体现和重建图像信息。对此本文提出一种基于小波变换的多通道多视角图像融合算法。由于小波变换将图像变换到不同的尺度域上,比一般的非尺度变换能提供更多的细节特征,因此在图像处理领域有广泛的应用[15-19]。本文提出的算法分为两个阶段,第一阶段为多通道融合形成单视角图像,具体是对小波变换后的高频分量采用平均梯度增强的加权融合算法,低频分量采用平均加权融合,后经小波反变换形成单视角图像;第二阶段为多视角图像融合形成全景图像,具体是对多幅单视角图像进行小波变换后的高频分量采用对比度增强的加权融合算法,低频分量仍采用平均加权融合。最后,将融合后的低频和高频图像用小波反变换便得到一幅完整的全景图像。

1 成像模型建立

系统平行墙体放置,置于x-y平面。成像区域可以被理解成M×N数据平面(m=1,2,3,…,M和n=1,2,3,…,N)。

条带SAR建筑布局成像的探测模式可作如下描述：如图1所示,以正侧视为例,在视角K(K=1,2,3,4)下,雷达平行墙体进行孔径合成探测,并以固定的波束指向发射脉冲重复频率为fPRF的脉冲串信号,接收机在此时间内接收建筑布局的回波信号,并完成接收信号在I/Q解调和数字化(A/D)处理,为处理机提供原始数据。

图1 条带SAR建筑布局成像回波模型

假设在视角1下进行合成孔径探测,s(τ)为雷达宽带传输信号,那么成像区域位于位置(m,n)的像素值可以用信号的传播时延来表示。在x-y数据平面上位于坐标(m,n)的目标值ζmn(t)在雷达坐标(p,q)可以表示成：

式中,ξ(p,q)为窗函数(通常是汉明窗),用来抑制旁瓣;(p,q)为时域时延补偿。回波信号ϑ(t)是发射信号的时延,即s′mn(t)=s(t-τmn(p,q))。令(t)=s(-t)表示与发射信号匹配的滤波器,那么f mn可表示为

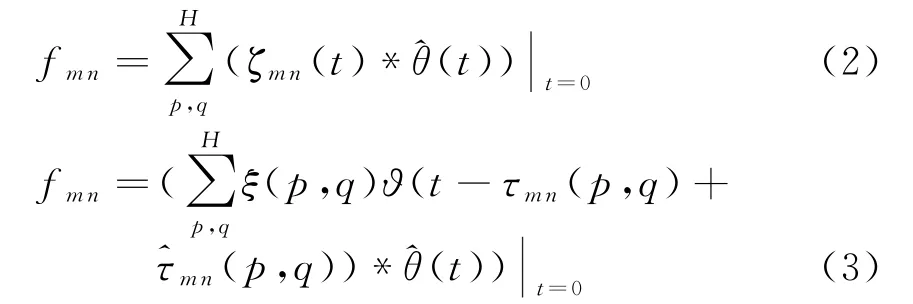
其中的时延补偿(p,q)在已知墙体参数的情况下,可以用固定时延算法、最短距离算法或速度补偿算法估计[20],此便是BP成像算法的思想。经过上述处理,可以得出区域的成像：

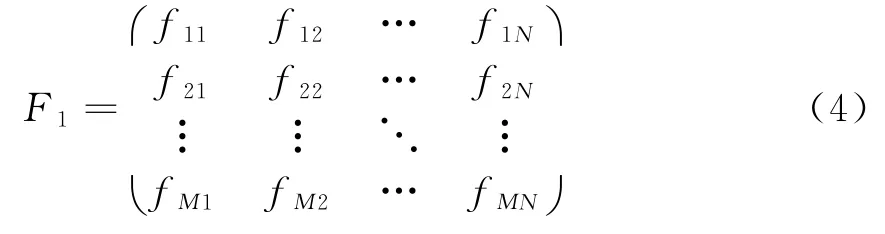
如此得到的F1便是在视角1条带SAR探测得到的原始图像矩阵。同样可以得到其余视角探测下得到原始图像矩阵F2,F3和F4。

2 算法描述

本阶段涉及两阶段小波融合算法。第一阶段,即单视角下的多通道图像融合,对各个单通道图像进行小波分解,低频近似分量采用平均加权融合,高频细节分量采用基于平均梯度增强的加权融合算法,如此再经小波反变换后便得到各个单视角下的融合子图像;第二阶段,即多视角图像融合过程,对各个单视角子图像进行小波分解,低频近似分量仍采用平均加权融合,高频细节分量采用基于对比度增强的加权融合算法,最终经小波反变换得到一幅全景图像。

平均梯度可敏感地反映图像对细节反差表达的能力,用来评价图像的模糊程度。一般来说,平均梯度越大,图像层次越多,表示图像越清晰。在单视角图像中,各个通道的图像只能部分反映该视角下的成像结果,且由于孔径限制,成像结果的分辨率不甚理想。因此在单视角多通道图像小波融合过程中,融合权重可基于平均梯度增强选取。对于任意两幅单通道建筑布局图像,基于平均梯度增强的小波变换法的图像融合处理流程如图2所示。

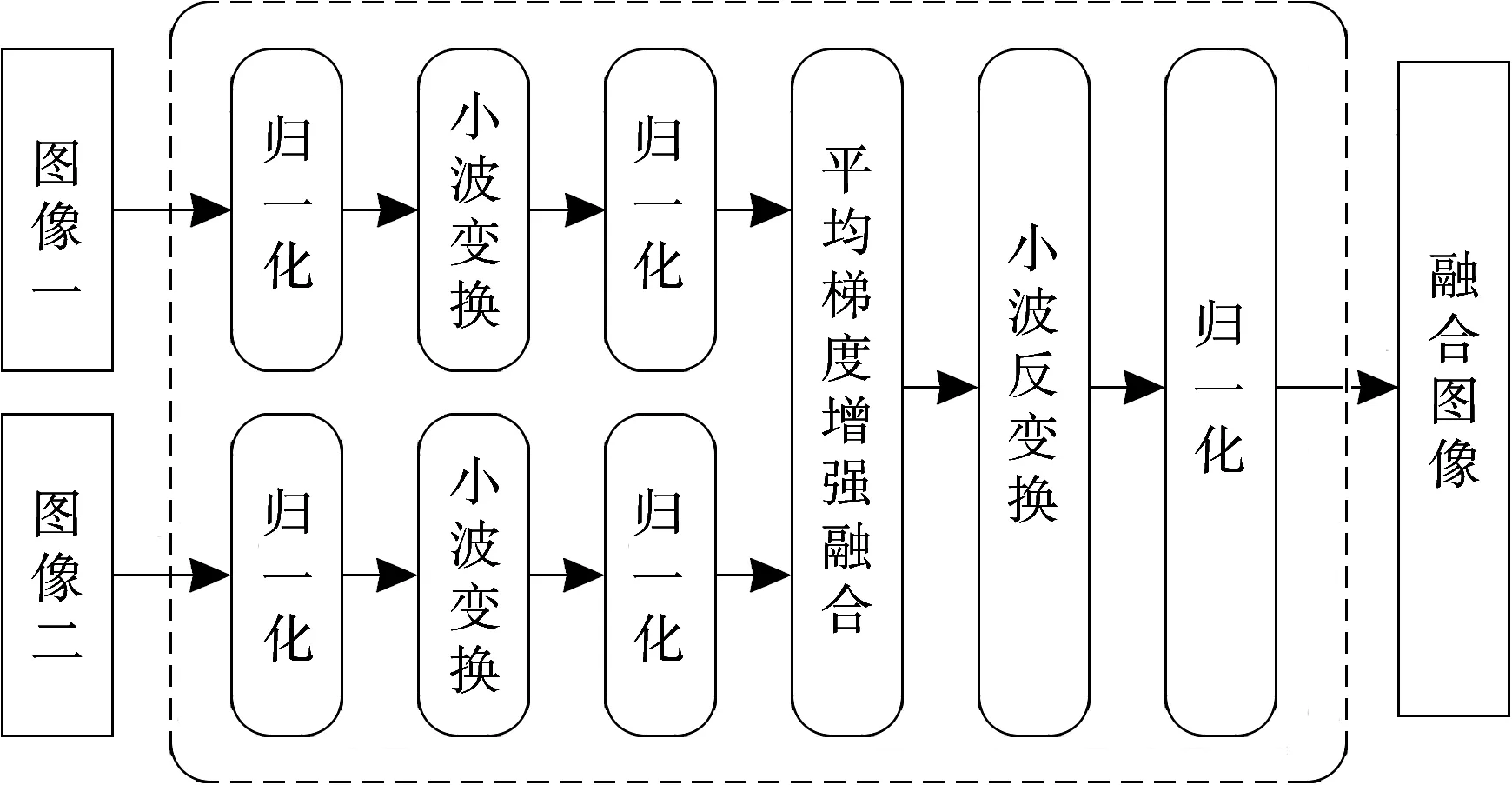
图2 基于平均梯度增强的小波变换融合处理流程图

此阶段下融合规则表示为

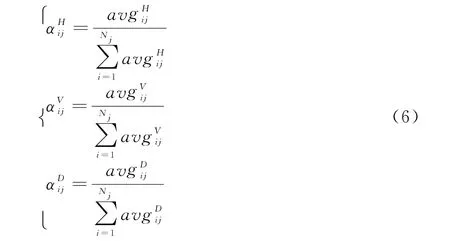
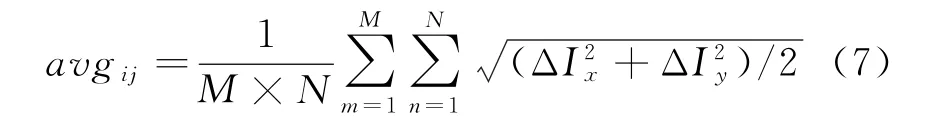
式中,ΔI x和ΔI y分别为x和y方向上的差分,M和N分别为图像矩阵的行数和列数。标准差反映了图像灰度相对于灰度平均值的离散情况,用来评价图像方差的大小。若标准差大,则图像灰度级分布分散,图像的反差大;否则图像反差小,对比度不大,色调单一均匀,看不出太多的信息。在第二阶段中,针对多通道图像融合形成的多幅单视角建筑布局图像,多幅图像中不同方向高频分量对比度不同,对比度能够近似反映目标墙体图像的边缘信息,提出基于对比度增强的小波变换融合算法,通过对小波变换后的高频图像采用基于对比度增强的加权融合,低频图像采用平均分量加权融合。克服了空域融合算法所带来的墙体展宽、边缘毛刺等缺陷,实现了多幅单视角图像目标墙体细节信息的“有效”融合,最终形成较高复原度、整齐的建筑布局全景图像。

对于任意两幅单视角建筑布局图像,基于对比度增强的小波变换图像融合处理流程如图3所示。

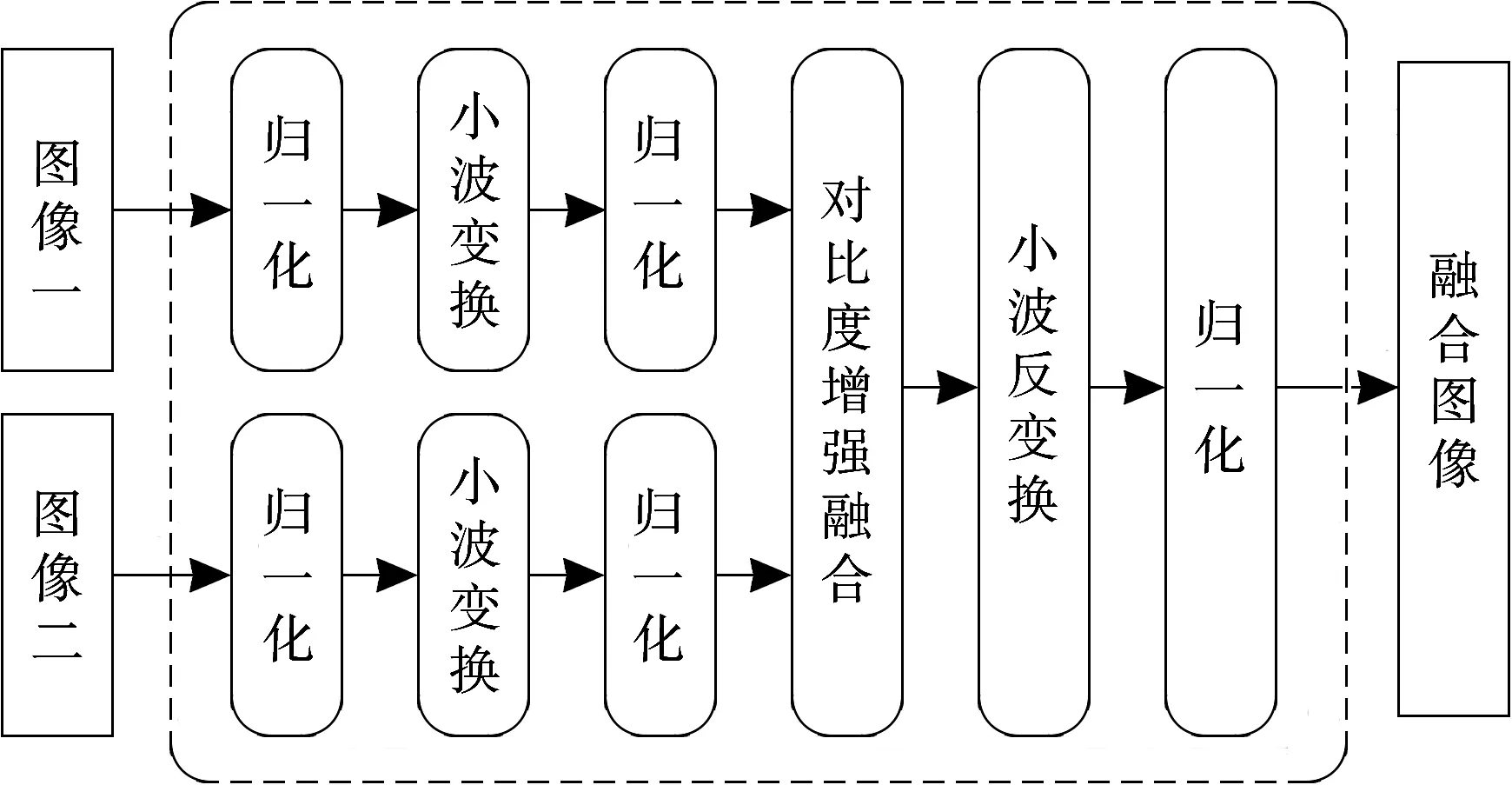
图3 基于对比度增强的小波变换图像融合处理流程

此阶段下的融合规则为

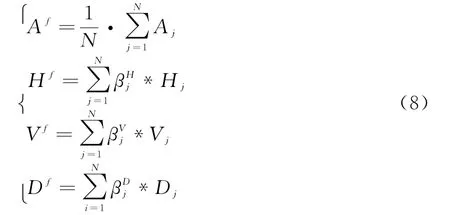
式中,N代表视角数目;A f,H f,V f,D f分别代表最终融合图像经小波分解后的低频近似分量、水平高频分量、垂直高频分量和斜45°角高频分量;分别代表相应分量下的权重,权重选取规则如下：

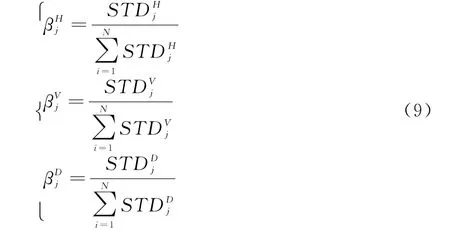
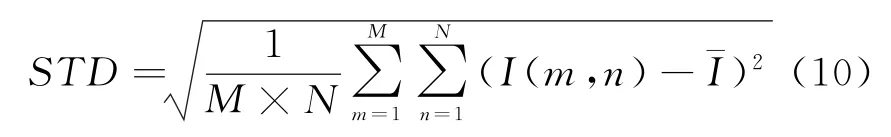
式中,¯I表示图像矩阵I均值,M和N分别表示图像矩阵的行数和列数。

最后,将融合后的低频分量和各个高频分量经小波反变换后便得到一幅全景图像。由于在算法中分别用到了基于平均梯度增强和对比度增强的融合规则,最终图像中的细节信息和清晰度将得到提升。如此基于多尺度域的SAR图像融合方法能在图像的不同尺度域上利用相应的细节和边缘信息进行融合和去噪,理论上显然比单尺度的融合效果要优越。

3 实验验证

3.1 XFDTD仿真试验验证

仿真场景设置如图4所示,采用一发两收偶极子天线分别沿四个与墙体垂直且相互垂直的视角进行合成孔径探测,收发天线间距0.15 m,移动间隔0.2 m,在视角1和视角3合成孔径长度为5 m的均匀线阵列,在视角2和视角4合成孔径长度为6 m的均匀线阵列。均匀介质墙体厚度为0.2 m,介电常数为4.5。

图4 建筑布局成像实验设置

针对每个视角下两个接收通道合成孔径回波,经过后向投影(BP)成像算法和基于平均梯度增强的小波变换图像融合后,处理结果如图5～8所示。

上述仿真结果显示,在单视角多通道建筑布局图像的小波融合过程中,基于平均梯度选取高频图像的融合权重,实现不同细节信息的互补,凸现了墙体图像完整的细节信息。仿真结果显示基于平均梯度增强的小波变换融合结果的图像层次分明,清晰度高。

针对多通道图像融合形成的四幅单视角建筑布局图像,通过基于对比度增强的小波变换图像融合算法处理,融合后的图像如图9所示。

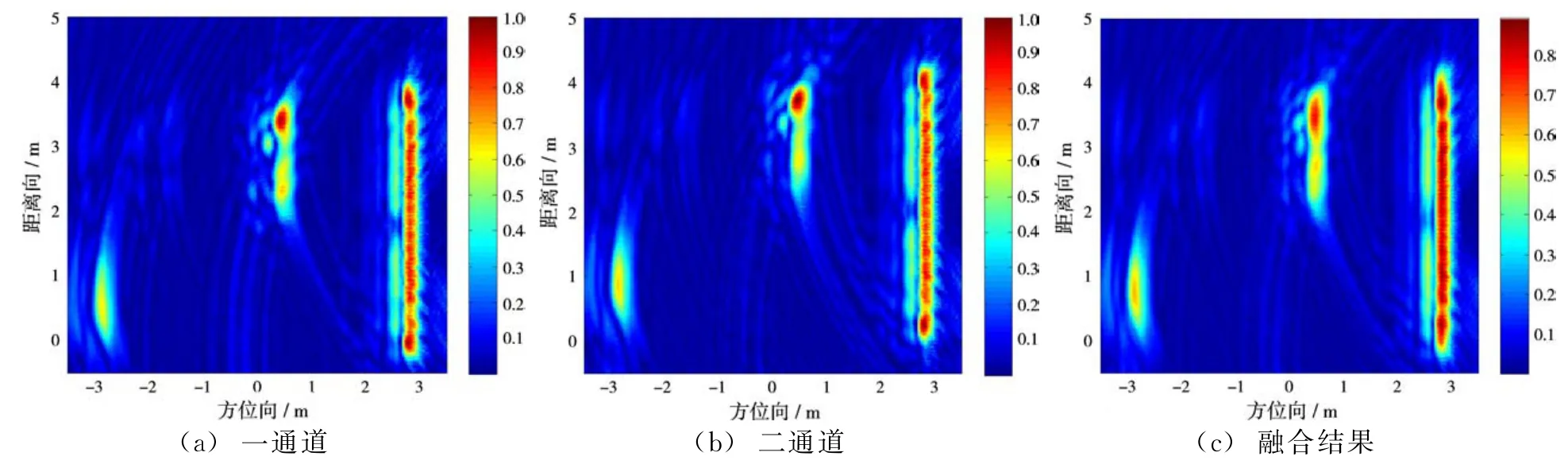
图5 视角1

图6 视角2

图7 视角3

图8 视角4

采用自动门限阈值分割方法(OSTU)[21]获取门限值,二值化后的图像如图10所示。

图9 小波变换融合最终结果

(a)小波变换融合图像的二值化结果(XFDTD)

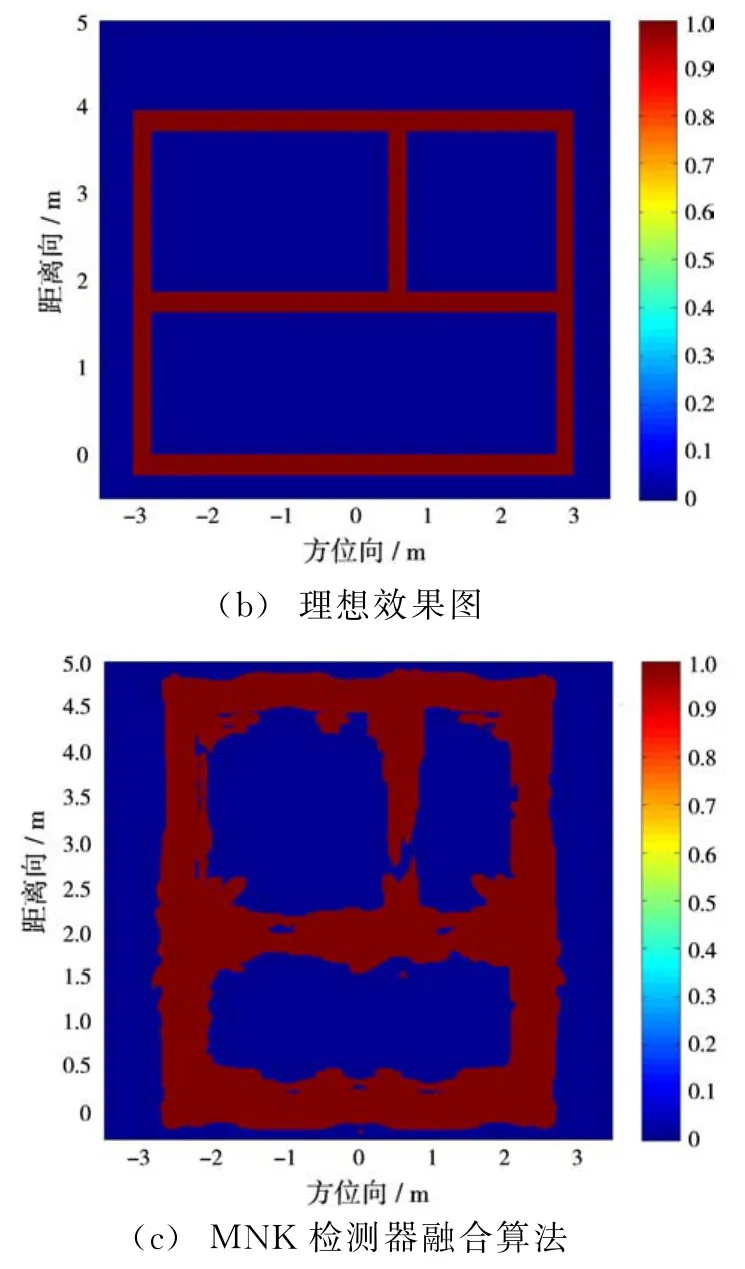
图10 建筑布局成像

由图10可以看出,与文献[20]提出的MNK检测器融合算法结果比较,本文提出的基于多尺度几何分析SAR图像融合算法在改善图像边缘“毛刺”,保证墙体厚度,恢复内层墙体强度等方面有较大优势,更接近理想效果图。

为量化说明算法的优越性,这里给出建筑布局图像复原度(DOR,degree of reducibility)的定义：

式中,M,N分别表示图像方位向和距离向的像素点数目;fb(x m,y n)表示形成的墙体图像经过二值化后的图像;Rb(x m,y n)表示真实墙体的理想分布图像。经计算,基于小波变换的多通道多视角图像融合算法处理后的图像复原度达到了78%,而MNK检测器融合算法处理结果的图像复原度只有67%。

3.2 穿墙雷达实验结果与分析

本次实验基于建筑环境中实测数据,场景设置如图11所示。

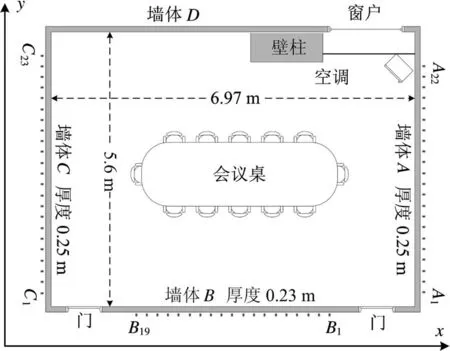
图11 实测场景

实验采用三视角多通道成像,视角分别是A侧视角、B侧视角和C侧视角,通道分别是A1、A22,B1、B19和C1、C23,天线摆放位置类似于图4,这里不再赘述。需要特别指出的是,在对B视角成像过程中,由于墙体D回波较弱,采用分块成像的方法。对第一阶段的单视角多通道图像融合采用本文提出的基于平均梯度增强的小波融合算法,对第二阶段的多视角图像融合采用基于对比度增强的小波融合算法,成像结果如图12～14所示。

图12 视角1

图14 视角3

针对基于平均梯度增强的小波融合形成的三幅单视角建筑布局图像,通过基于对比度增强的小波变换图像融合算法,融合后的图像如图15所示。

同样,采用自动门限阈值分割方法(OSTU)[22]获取门限值,二值化后的图像如图16所示。

同样根据本文提出的图像复原度的定义,得到经实测数据处理后图像复原度达到71%。

以上所示的仿真和实测数据处理结果显示,基于小波变换图像融合算法能够在不同尺度上完成对多幅图像的较好融合,实现了墙体边缘等细节信息的“有效”融合,保证了目标墙体区域与非目标杂波区域的界限的清晰度,形成较高复原度、整齐的建筑布局全景图像。

4 结束语

本文提出基于多尺度几何分析SAR图像融合算法,并将其用于穿墙建筑布局场景成像中。该算法较一般的融合算法在处理融合图像交汇墙体强度过强、内层墙体恢复、均方差降低和信噪比提高等方面有较大优势。该算法分成两个阶段,即多通道图像融合和多视角图像融合。在第一阶段各个单视角下的多通道图像融合过程中,为锐化融合图像的边缘信息,采用基于平均梯度增强的小波融合算法。在第二阶段多视角图像融合过程中,为提高融合图像的对比度,并改善图像的细节信息,采用基于标准差选大的小波融合算法。相比其他融合算法,如文献[21]提出的MNK检测器融合算法等只在图像的单尺度域上进行处理,这样必然丧失了很多不同尺度域下的细节信息。而采用本文提出的基于多尺度几何分析的SAR图像融合方法能利用图像在不同尺度域上的细节和边缘信息进行融合和去噪,仿真和实测数据处理结果验证了经该算法处理后的图像细节信息和清晰度能够得到较大提升。

图15 小波变换融合最终结果

图16 二值化的图像结果

[1]CHEN V C,SMITH G E,WOODBRIDGE K,et al.Through-the-Wall Radar Imaging[M].Pennsylvania,USA：CRC Press,2010.

[2]SMITH G E,MOBASSERI B G.Robust Throughthe-Wall Radar Image Classification Using a Target-Model Alignment Procedure[J].IEEE Trans on Image Processing,2012,21(2)：754-767.

[3]DEBES C,ZOUBIR A M,AMIN M G.Enhanced Detection Using Target Polarization Signatures in Through-the-Wall Radar Imaging[J].IEEE Trans on Geoscience and Remote Sensing,2012,50(5)：1968-1979.

[4]LAGUNAS E,AMIN M G,AHMAD F,et al.Sparsity-Based Radar Imaging of Building Structures[C]∥2012 Proceedings of the 20th European Signal Processing Conference(EUSIPCO),Bucharest：IEEE,2012：864-868.

[5]LAGUNAS E,AMIN M G,AHMAD F,et al.Determining Building Interior Structures Using Compressive Sensing[J].Journal of Electronic Imaging,2013,22(2)：021003.

[6]AFTANAS M,DRUTAROVSKýM.Imaging of the Building Contours with Through the Wall UWB Radar System[J].Radioengineering,2009,18(3)：258-264.

[7]LANARI R,TESAURO M,SANSOSTI E,et al.Spotlight SAR Data Focusing Based on a Two-Step Processing Approach[J].IEEE Trans on Geoscience and Remote Sensing,2001,39(9)：1993-2004.

[8]FARINA A,MORABITO F C,SERPICO S,et al.Fusion of Radar Images：State of Art and Perspective[C]∥2001 CIE International Conference on Radar,Beijing,China：[s.n.],2001：9-15.

[9]GOUINAUD C.SAR Image Fusion in Multi Sensor Context for Small Urban Area Detection[C∥IEEE International Geoscience and Remote Sensing Symposium,Boston,MA：IEEE,2008：Ⅲ-988-Ⅲ-991.

[10]PAPSON S,NARAYANAN R M.Multiple Location SAR/ISAR Image Fusion for Enhanced Characterization of Targets[C]∥Proceedings of the SPIE,Orlando,FL,USA：[s.n.],2005：128-139.

[11]SENG C H,BOUZERDOUM A,PHUNG S L,et al.A Two-Stage Image Fusion Method for Enhanced Through-the-Wall Radar Target Detection[C]∥2011 IEEE Radar Conference(RADAR),Kansas,MO：IEEE,2011：643-647.

[12]ROVNAKOVA J,KOCUR D.Data Fusion from UWB Radar Network：Preliminary Experimental Results[C]∥2011 21st International Conference Radioelektronika,Brno：IEEE,2011：1-4.

[13]HU H,LIN X,LI Z.Reconstruction of Panoramic Image Through Fusion of Sequential Lateral Multi-Lens Logging Images[C]∥2012 International Conference on Information and Automation(ICIA),Shenyang：IEEE,2012：334-337.

[14]SENG C H,BOUZERDOUM A,AMIN M G,et al.Two-Stage Fuzzy Fusion with Applications to Through-the-Wall Radar Imaging[J].IEEE Geoscience and Remote Sensing Letters,2013,10(4)：687-691.

[15]潘湘岳,宋建社,吴建新.基于数据融合的SAR图像斑点噪声抑制[J].雷达科学与技术,2007,5(6)：443-446.PAN Xiang-yue,SONG Jian-she,WU Jian-xin.An Improved Speckle Reduction Algorithm of SAR Image Based on Data Fusion[J].Radar Science and Technology,2007,5(6)：443-446.(in Chinese)

[16]LIU Guixi,CHEN Wenjin,LING Wenjie.An Image Fusion Method Based on Directional Contrast and Area-Based Standard Deviation[J].Journal of Scientific Instrument,2005,26(6)：628-631.

[17]CHIBANI Y.Multisource Image Fusion by Using the Redundant Wavelet Decomposition[C]∥2003 IEEE International Geoscience and Remote Sensing Symposium,[S.l.]：IEEE,2003：1383-1385.

[18]KHANDELWAL P,SINGH K K,SINGH B K,et al.Unsupervised Change Detection of Multispectral Images Using Wavelet Fusion and Kohonen Clustering Network[J].International Journal of Engineering and Technology,2013,5(2)：1401-1406.

[19]RUBIO-GUIVERNAU J L,GURCHENKOV V,LUENGO-OROZ M A,et al.Wavelet-Based Image Fusion in Multi-View Three-Dimensional Microscopy[J].Bioinformatics,2012,28(2)：238-245.

[20]崔国龙.超宽带雷达合成孔径成像算法研究与实现[D].成都：电子科技大学,2008.

[21]贾勇,孔令讲,马静,等.穿墙雷达多视角建筑布局成像[J].电子与信息学报,2013,35(5)：1114-1119.

[22]FENG B,WANG Z,SUN J.Image Threshold Segmentation with Ostu Based on Quantum-Behaved Particle Swarm Algorithm[J].Computer Engineering and Design,2008,29(13)：3429-3434.