SAE9310钢动态再结晶临界条件的研究

黄顺喆， 厉勇， 王春旭， 韩 顺， 刘宪民， 田志凌

(1.钢铁研究总院特殊钢研究所，北京100081;2.中国钢研科技集团有限公司，北京100081)

动态再结晶临界应变通常用作判断材料在热变形过程中是否发生动态再结晶，对材料热变形过程中工艺控制有重要的指导意义，确定材料在热变形中的临界应变量是建立临界应变预测模型的关键条件［1］。如果材料的应力-应变曲线上出现峰值σp，那么可以认为发生了动态再结晶行为，但研究中把峰值应力对应的应变εp看做临界应变εc是不科学的，事实上动态再结晶在应变量未达到峰值应变εp时就已经发生［2，3］。材料的加工硬化率 (θ= dσ/dε)表征流变应力随应变的变化速率，流变曲线是热变形时材料微观组织的外在表现，一般很难直接从曲线上来确定发生动态再结晶的临界应变，而加工硬化率曲线则能反映材料内部组织的变化特征［4，5］。Poliak［2，3］认为，材料发生动态再结晶软化时，不管应力-应变曲线上是否出现应力峰，其θ-σ曲线上均呈现拐点，并认为临界条件与dθ/dσ-σ曲线上的最大值以及θ-σ曲线上的拐点相对应。很多学者［1，6～9］应用加工硬化理论，在判断材料发生动态再结晶的临界应变方面取得较好的成果。

SAE9310钢是国内外广泛使用的航空用低成本、高强度渗碳钢，其强度高韧性好，且淬透性和可焊性良好，多用于制造截面尺寸较大且受重载荷的传动构件，如航空领域中的关键齿轮、齿轮轴、主旋翼轴、尾桨轴等传动装置［10-13］。本文基于加工硬化理论，通过热模拟实验获得的应力-应变曲线数据，研究SAE9310钢在大应变条件下的加工硬化率曲线、动态再结晶的拐点判据以及动态再结晶的临界条件。

1 实验材料及方法

实验采用真空感应+真空自耗重熔冶炼的SAE9310钢(以下简称实验钢)，其化学成分为(质量分数/%):C 0.11，Cr 1.25，Ni3.22，Mo 0.13，Mn 0.68，Si0.26，其余为Fe。钢锭经高温扩散退火后，锻造成材，将试样加工成尺寸为φ10mm×15mm的圆柱形压缩试样后，在Gleeble-3800热模拟实验机上进行等温恒应变速率的轴向压缩实验，测得该钢的高温流变曲线。变形温度为900℃，1000℃，1100℃，1200℃，变形速率为0.01s-1，0.1s-1，1s-1，10s-1，最大真应变为0.9，变形后立刻喷水淬火，以分析其高温组织。用线切割机把热压缩试样沿压缩方向从中间剖开，磨平、抛光后，用饱和苦味酸水溶液+少量洗剂灵溶液腐蚀奥氏体晶界，用光学显微镜观察显微组织。

2 实验结果与分析

2.1 加工硬化理论

材料在加工过程中的流变应力与位错密度的变化存在如下关系［14］:

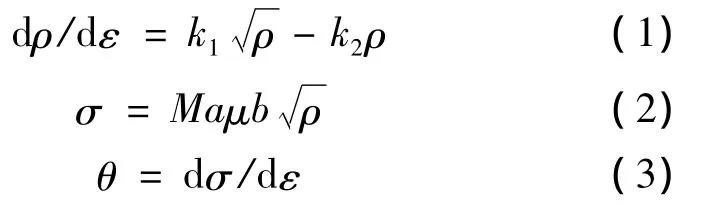
式中:σ为流变应力(MPa)，ε为真应变，ρ为位错密度(m-3)，M为Taylor因子，μ为剪切模量，θ为加工硬化率，其他为材料常数。式(1)，(2)，(3)表明:材料的加工硬化率θ与位错密度ρ有关。根据加工硬化理论［15-21］，材料的加工硬化率随应力变化的规律可分为五个阶段，分别是Ⅰ-易滑移阶段、Ⅱ-线性硬化阶段、Ⅲ-动态回复硬化阶段、Ⅳ-大应变硬化阶段、Ⅴ-动态再结晶软化阶段，如图1所示。

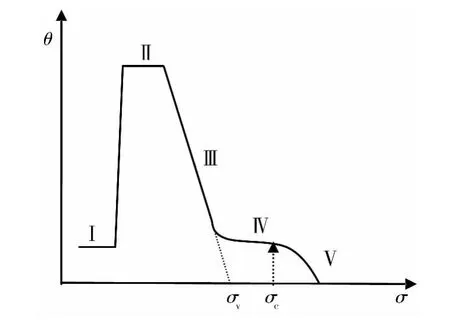
图1 加工硬化率θ随应力σ变化示意图［1］Fig.1 Sketchmap of strain hardening rateθand stressσ

本工作重点研究第Ⅴ阶段-动态再结晶软化阶段。在这一阶段里，变形进行到一定程度后，变形组织内部的位错密度达到一定的临界值，开始发生动态再结晶，此时材料的θ-σ曲线上呈现拐点特征，拐点处对应的应力即是动态再结晶临界应力σc［20，22］原字符串，且lnθ-lnσ曲线与lnθ-ε曲线上均呈现拐点特征［22］，由此通过分析应变硬化速率θ与流变应力σ曲线上的拐点或者-∂θ/∂σ-σ曲线上的最小值，即可得到动态再结晶的临界条件。

2.2 临界应变的确定

SAE9310钢在不同变形条件下的高温流变曲线表现为动态回复型和动态再结晶型，如图2所示。由图可知，当变形温度为900℃时，实验钢在不同应变速率下的真应力-真应变曲线均表现为动态回复型，随着变形温度的提高，实验钢的真应力-真应变曲线可明显分为两种类型:动态回复型和具有单峰特征的动态再结晶型。材料的应力-应变曲线上出现峰值意味着材料内部组织发生了动态再结晶，但应力-应变曲线并不能直观的反应材料发生动态再结晶的临界条件［1，3］。应用加工硬化理论，对应力-应变曲线数据进行处理，得到θ-σ曲线及dθ/dσ-σ曲线，采用加工硬化率拐点判据来判断发生动态再结晶的临界应力σc和临界应变εc。为了确定应力-应变曲线上各应变下的斜率，先对曲线进行拟合，再对拟合方程求导，从而得到各应变下的斜率，然后绘制加工硬化率θ与真应力σ的关系曲线，进而确定发生动态再结晶的临界条件。

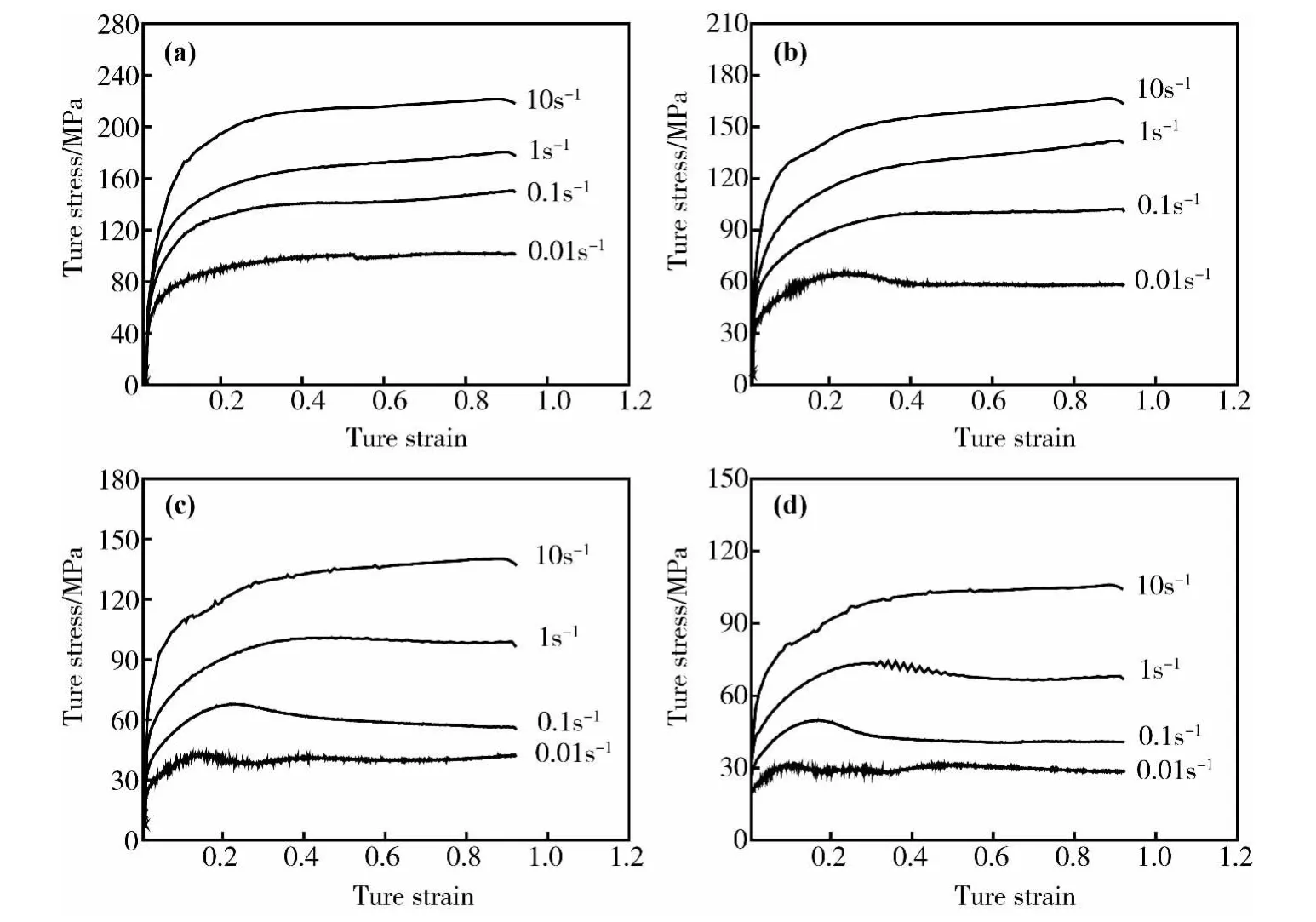
图2 SAE9310钢在不同变形条件下的高温流变曲线Fig.2 True stress-strain curves of SAE9310 steel at different deformation conditions (a)900℃;(b)1000℃;(c)1100℃;(d)1200℃

以变形温度为1100℃，应变速率为0.1s-1时的真应力-真应变曲线为例，见图3所示，对图中曲线中应力σ从0到峰值应力σp段进行拟合，得到此变形阶段各应力对应的加工硬化率θ。求得各应变下的加工硬化率θ，得到加工硬化率θ与真应力σ关系曲线，如图4a所示。对图中曲线进行3次多项式拟合得到θ-σ方程:

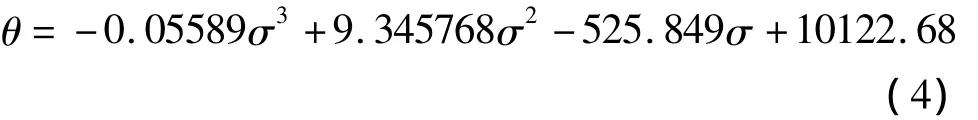
对方程(4)求导并绘制dθ/dσ-σ曲线，如图4b所示。当d2θ/dσ2=0时对应的应力σ即为临界应力σc，对应的应变ε即为临界应变εc，求得在变形条件为 1100℃，应变速率为 0.1s-1时 SAE9310钢的临界应力σc为55.8MPa，对应临界应变εc为 0.09。同理得到不同变形条件下SAE9310钢的加工硬化率θ与应力σ的关系曲线，见图5所示，为了确定θ-σ曲线中拐点数值，对图中曲线求一阶偏导，结果如图6所示。

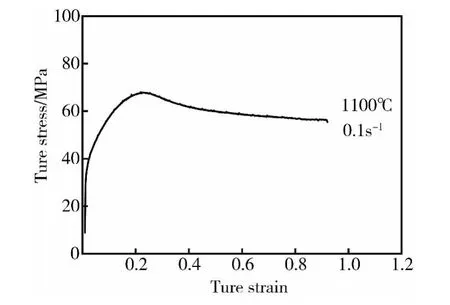
图3 应变速率为0.1s-1时SAE9310钢的真应力-真应变曲线Fig.3 True stress-true strain cures of SAE9310 steel deformed at strain rate of 0.1s-1

图4 变形条件为1100℃，0.1s-1时的θ-σ关系曲线(a)及dθ/dσ-σ曲线(b)Fig.4 Curves ofθversusσ(a)and dθ/dσversusσ(b)deformed at1100℃ with 0.1 s-1

根据图5、图6可得到SAE9310钢在不同应变速率和变形温度下发生动态再结晶的临界应力和临界应变，如图7、图8所示。由图可知，当变形温度一定时，随着应变速率的增加，临界应变和临界应力都相应提高;而当变形速率一定时，提高变形温度，临界应变和临界应力均降低。

Z参数(Zener-Hollomon参数)被广泛用以表征变形温度及应变速率对热变形过程的综合作用。在热变形过程中有［23］:

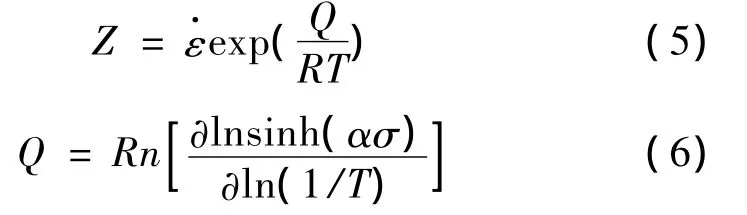
临界应变εc和峰值应变εp与Z参数的关系如图9所示。由图可知，Z参数能反应临界应变及峰值应变与变形条件的变化规律;临界应变与热加工参数Z是密切相关的，临界应变与峰值应变均随Z参数的增大而增加，且临界应变与峰值应变之间存在一定相关性，比值约为εc/εp=0.30～0.42。

2.3 组织演变与动态再结晶状态图

图10为SAE9310钢在变形温度为1100℃、应变速率为0.1s-1条件下的加工硬化率与真应变的关系曲线，曲线中所标A，B，C，D对应应变分别为临界应变εc、峰值应变εp、最大软化率处应变ε*和稳态流变应力对应应变 εs，图11为对应四点的金相组织。

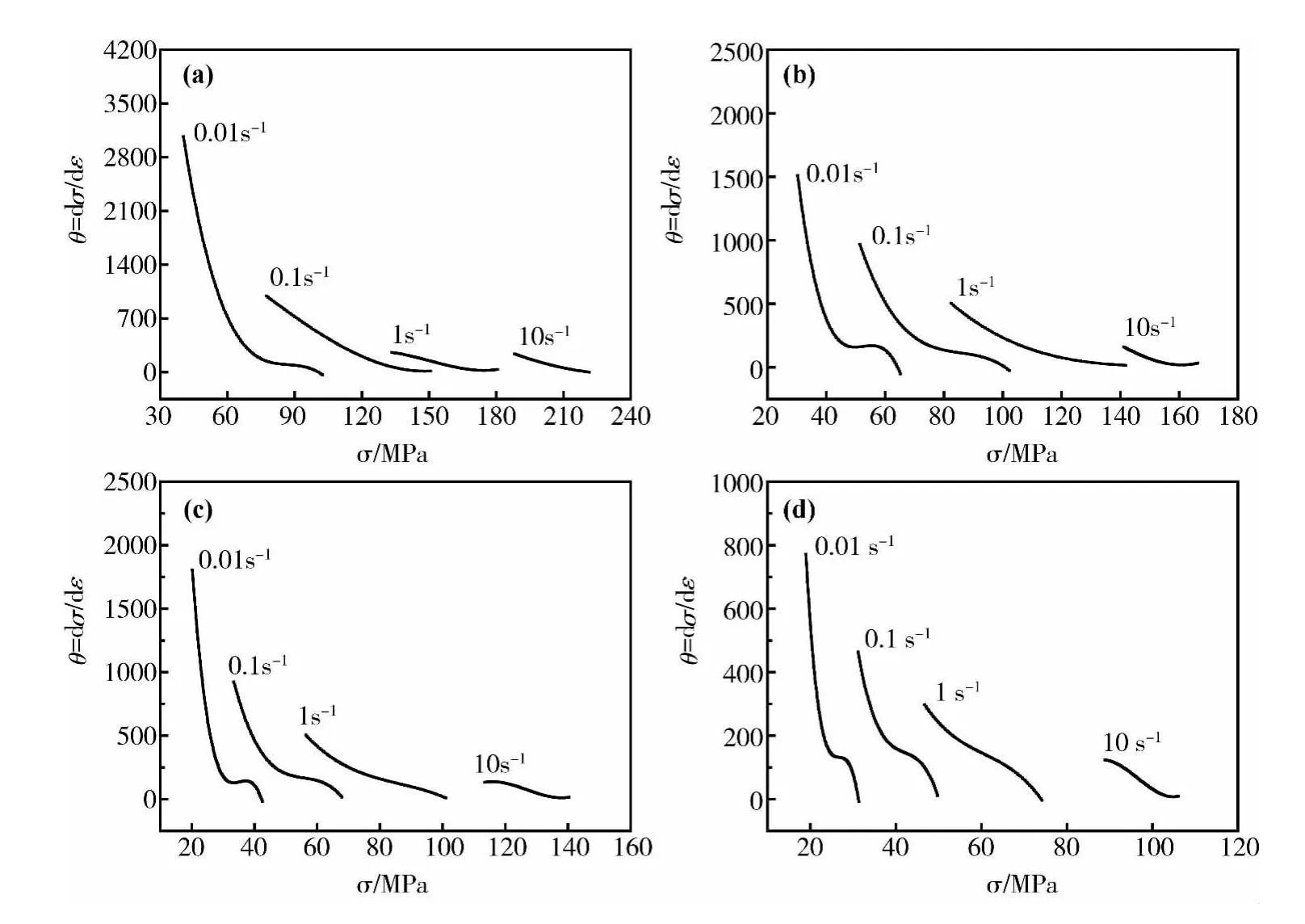
图5 不同变形温度下SAE9310钢的θ-σ关系曲线Fig.5 Curves ofθversusσfor SAE9310 steel under different deformation temperatures (a)900℃;(b)1000℃;(c)1100℃;(d)1200℃

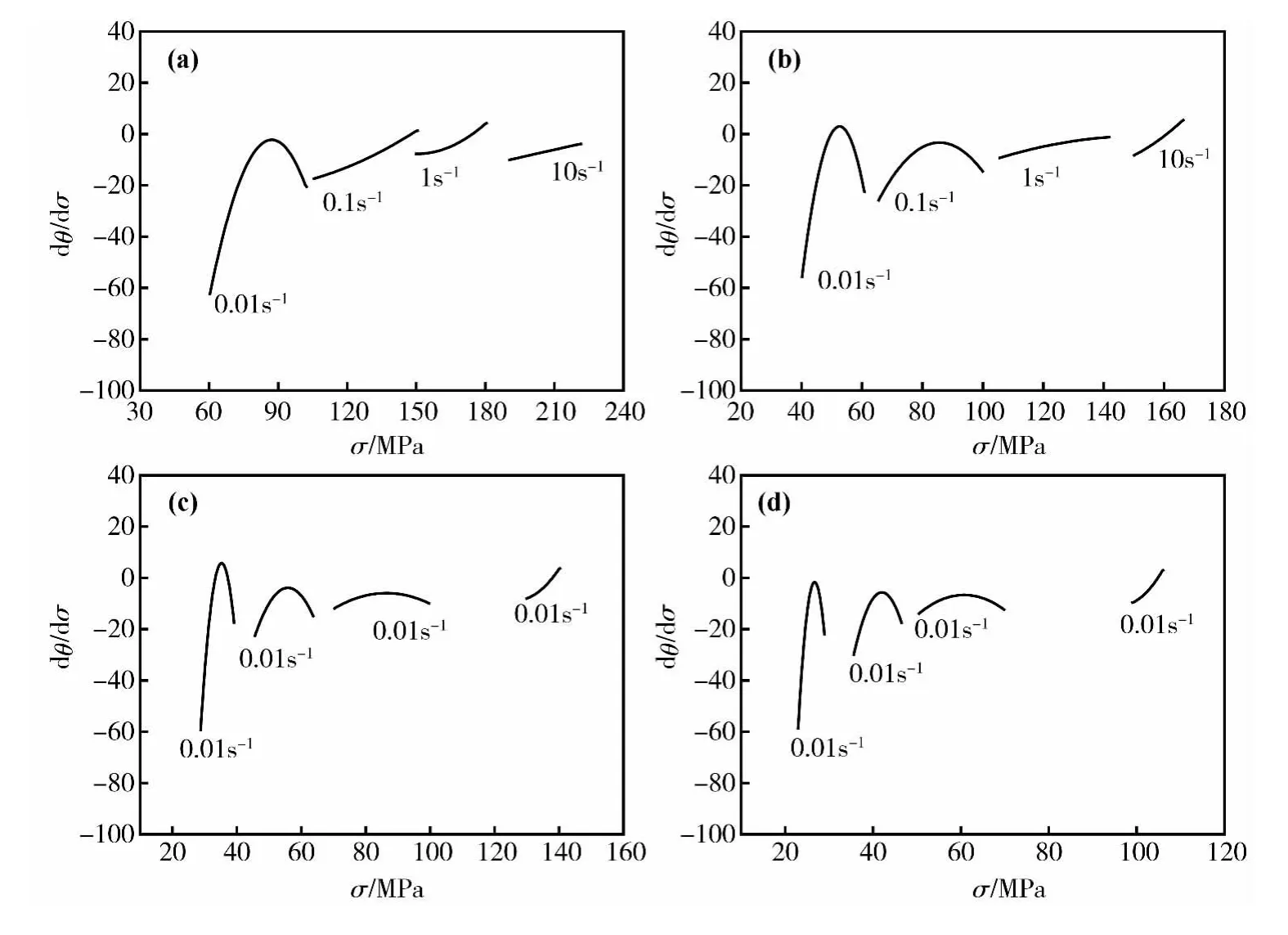
图6 不同变形温度下SAE9310钢的dθ/dσ-σ关系曲线Fig.6 Curves of dθ/dσversusσfor SAE9310 steel under different deformation temperatures (a)900℃;(b)1000℃;(c)1100℃;(d)1200℃

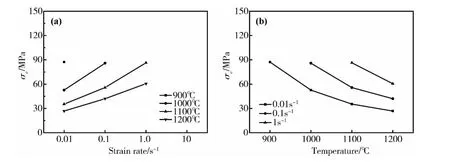
图7 不同变形条件下SAE9310钢的σc-˙ε曲线与σc-T曲线Fig.7 Curves ofσc versus˙εandσc versus T for SAE9310 steel under different deformation conditions

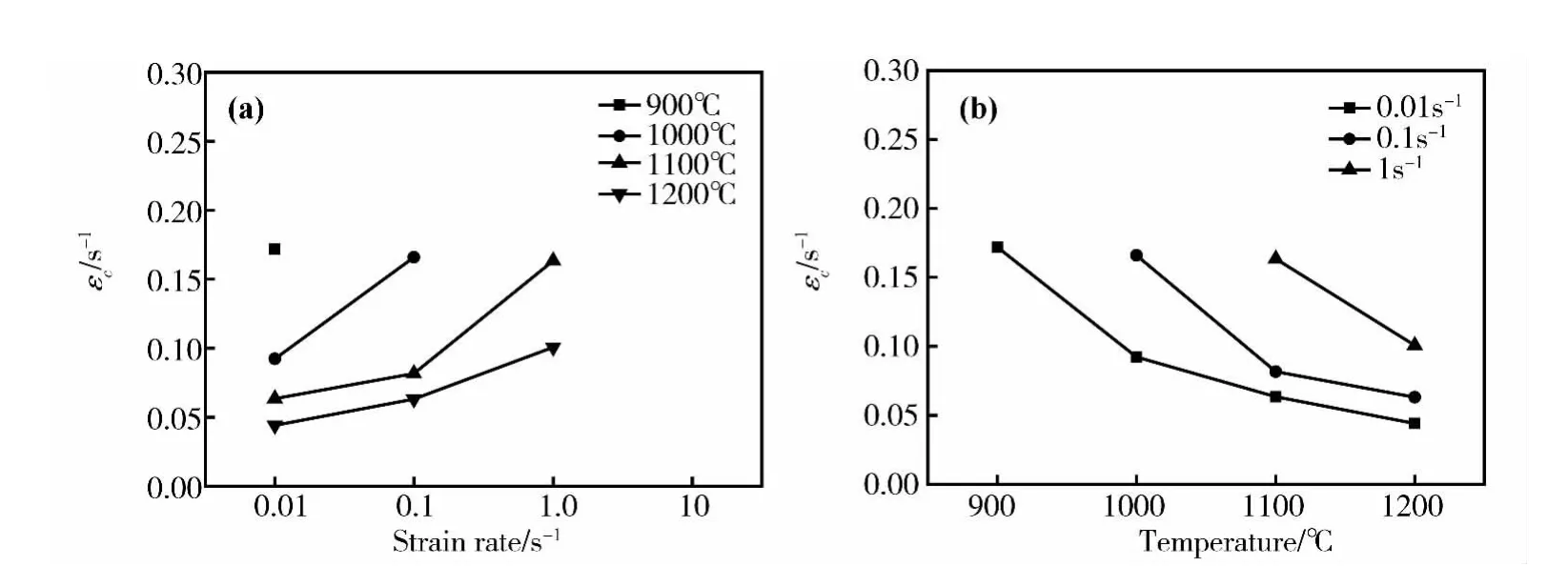
图8 不同变形条件下SAE9310钢的εc-˙ε曲线与εc-T曲线Fig.8 Curves ofεc versus˙εandεc versus T for SAE9310 steel under different deformation conditions

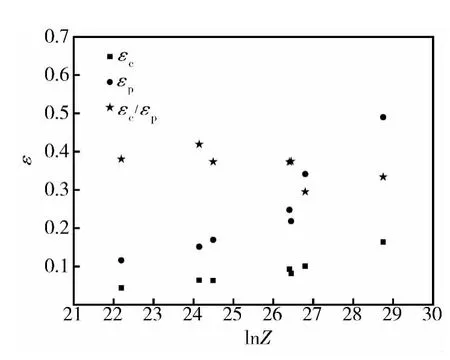
图9 Z参数与εc，εp的关系曲线Fig.9 Relationship between Z andεc，εp

在变形初期，实验钢的奥氏体晶粒被压扁、拉长，晶界发生局部迁移，当应变量达到临界应变εc时，少量新鲜等轴状动态再结晶晶粒在变形的原奥氏体晶界处形成(图11a);当应变量为峰值应变εp时，加工硬化率为0，实验钢发生部分动态再结晶，变形晶粒与等轴状再结晶晶粒共存(图11b)，此后动态再结晶软化作用将大于加工硬化作用;当应变量达到最大软化率处应变ε*时，加工硬化降到最小值，动态再结晶基本完成，金相组织变现为不均匀的再结晶晶粒(图11c);随着变形量的进一步增加，当位错密度增大产生的加工硬化和再结晶过程中软化作用趋于平衡时，流变曲线进入稳态阶段，此时组织为充分动态再结晶并发生长大的等轴状奥氏体晶粒(图11d)。

由实验数据绘得SAE9310钢的动态再结晶状态图，如图12所示，其中A区—加工硬化区，B区—部分动态再结晶区，C区—完全动态再结晶区，从动态再结晶状态图可以看出，随着Z参数的增加，即随着变形温度的降低和应变速率的增加，材料发生动态再结晶的临界变形量逐渐增加，也就是说发生动态再结晶变得较为困难。

3 结论

(1)SAE9310钢的应力-应变曲线随变形条件的不同出现两种类型的曲线特征，即动态再结晶型和动态回复型，两种类型曲线均可采用θ-σ曲线拐点判据来确定动态再结晶临界条件。

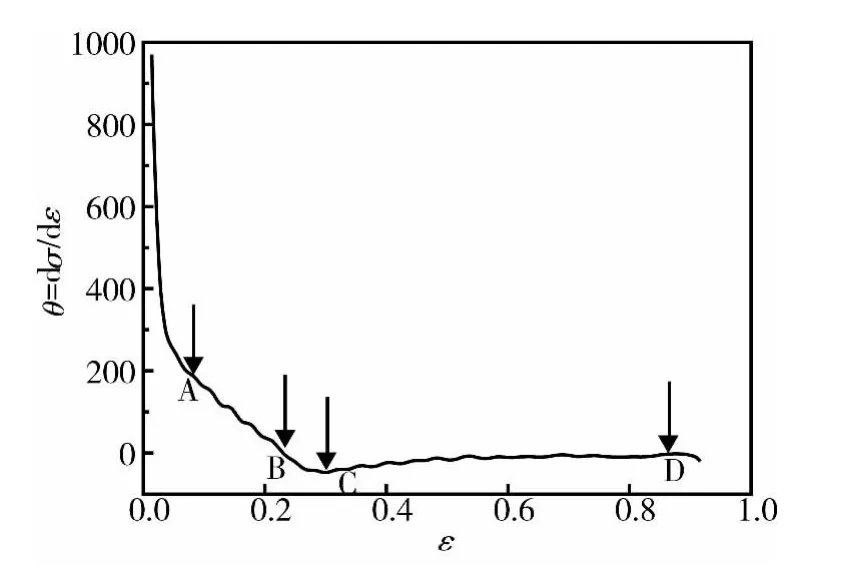
图10 变形条件为1100℃，0.1s-1时的θ-σ关系曲线Fig.10 Relationship betweenθandσ deformed at1100℃ with 0.1 s-1

图11 对应图10中点A，B，C，D处的金相组织Fig.11 Metallograph corresponding to point A，B，C，D in fig.10(a)A;(b)B;(c)C;(d)D

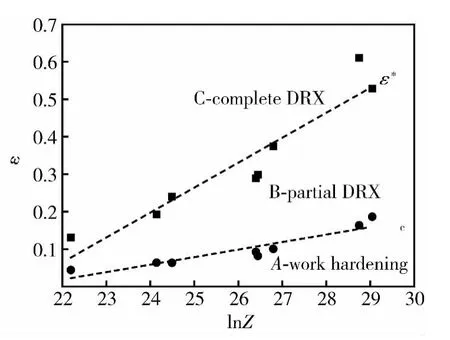
图12 SAE9310钢高温热变形的动态再结晶状态图Fig.12 State diagram of DRX for SAE9310 steel under hot temperature deformation

(2)SAE9310钢发生动态再结晶时，θ-σ曲线存在拐点，dθ/dσ-σ曲线上出现最大值，利用拐点判据可以确定9310钢发生动态再结晶的临界应变。

(3)SAE9310钢发生动态再结晶的临界应变εc和临界应力σc均随应变速率的增大和变形温度的降低而增加，临界应变与峰值应变之间满足εc/εp= 0.30～0.42。随着Z参数的增加，即随着变形温度的降低和应变速率的增加，实验钢发生动态再结晶的临界变形量逐渐增加，发生动态再结晶变得更加困难。

［1］欧阳德来，鲁世强，崔霞，等.应用加工硬化率研究TA15钛合金β区变形的动态再结晶临界条件［J］.航空材料学报，2010，30(2):17-23. (OUYANG D L，LU SQ，CUIX，et al.Study on critical strains of dynamic recrystallization duringβprocess in TA15 Titanium alloy using working hardening rate［J］. Journal of Aeronautical Materials，2010，30(2):17 -23.)

［2］POLIAK E I，JONASJJ.A one-parameter approach to determining the critical conditions for the initiation of dynamic recrystallization［J］.Acta Materialia，1996，44(1):127 -136.

［3］POLIAK E I，JONAS J J.Initiation of dynamic recrystallization in constantstrain rate hotdeformation［J］.ISIJInternational，2003，43(5):684-691.

［4］PRASAD G V，GOERDELER M，GOTTSTEIN G.Work hardening model based on multiple dislocation densities［J］.Materials Science and Engineering(A)，2005，400 -401;231-233.

［5］ROLLETT A D，KOCKS U F.A review of the stages of work hardening［J］.Solid State Phenomena，1993，35-36;1-18.

［6］GOTTSTEIN G，BRUNGER E，FROMMERT M，et al. Prediction of the critical conditions for dynamic recrystallization inmetals［J］.Zeitschrift for Metallkunde，2003，94 (5):628-635.

［7］POLIAK E I，JONAS J J.Critical strain for dynamic recrystallization in variable strain rate hot deformation［J］. ISIJ International，2003，43(5):692-700.

［8］NAJAFIZADEH A，JONAS JJ.Predicting the critical stress for initiation of dynamic recrystallization［J］.ISIJ International，2006，46(11):1679-1684.

［9］黄光杰，钱宝华，汪凌云，等.AZ31镁合金初始动态再结晶的临界条件研究［J］.稀有金属材料与工程，2007，36 (12):2080-2083. (HUANG G J，QIAN B H，WANG L Y，et al.Study on the critical conditions for initial dynamic recrystallization of AZ31 magnesium alloy［J］.Rare Metal Materials and Engineering，2007，36(12):2080-2083.

［10］周凤云，李熙章.高强度渗碳钢制构件的断裂分析［J］.理化检验-物理分册，2003，39(4):206-209. (ZHOU F Y，LIX Z.Fracture analysis of the components made of high strength and carburizing steel［J］.Physical Testing and Chemical Analysis Part A:Physical Testing，2003，39(4):206-209.)

［11］吴秋平，王春旭，刘宪民，等.回火温度对9310钢力学性能及组织的影响［J］.热加工工艺，2012，41(6): 179-183. (WU Q P，WANG C X，LIU X M，et al.Influence of tempering temperature on mechanical properties and microstructure of 9310 steel［J］.Hot Working Technology，2012，41(6):179-183.)

［12］黄顺喆，厉勇，王春旭，等.9310钢的奥氏体晶粒长大规律研究［J］.热加工工艺，2010，39(18):31-33. (HUANG SZ，LIY，WANG C X，et al.Study on growth law of austenite grain in 9310 steel［J］.Hot Working Technology，2010，39(18):31-33.)

［13］厉勇，王春旭，刘宪民，等.SAE9310钢奥氏体的冷却转变行为［J］.机械工程材料，2010，34(5):12-15. (LI Y，WANG C X，LIU X M，et al.Microstructure transformation behavior of austenite cooling for SAE9310 steel［J］.Mater Mech.Eng，2010，34(5):12-15.)

［14］ESTRIN Y.Dislocation theory based constitutive modeling:foundations and applications［J］.Journal of Materials Processing Technology，1998，80/81;33-39.

［15］UUN T，ZEHETBAUER M.Stage IV work hardening in cell forming materials，part II:a new mechanism［J］. Scripta Materialia，1996，35(12):1467-1473.

［16］GOTTSTEIN G，FROMMERTM，GOERDELER M，etal. Prediction of the critical conditions for dynamic recrystallization in the austenitic steel 800H［J］.Materials Science and Engineering(A)，2004，387/389;604-608.

［17］NABARRO F，BASINSKIZ S，HOLTD B.The plasticity of pure single crystals［J］.Advances in Physics，1964，13 (50):193-323.

［18］MECKING H，KOCKS U F.Kinetics of flow and strain hardening［J］.Acta Metall，1981，29(11):1865 -1875.

［19］KOCKSU F.Laws ofwork hardening and low-temperature creep［J］.JEng Mater Technol，1976，98(1):76-85.

［20］GIL S J，VAN H P，AERNOUDT E.Large strain work hardening and textures［J］.Progressing Materials Science，1980，25(2-4):69-134.

［21］MECKING H.Dislocation modeling of physical systems［M］.Oxford:Pergamon Press，1981:197-211.

［22］POLIAk E I，JONAS JJ.Initiation of dynamic recrystallization in constant strain rate hot deformation［J］.ISIJInternational，2003，43(5):684-691.

［23］MEDINA SF，HERNANDEZ C A.General expression of Zener-Hollomon parameter as a function of the chemical composition of low alloy and micro-ally steels［J］.Acta Materialia，1996，44(1):137-1548.