基于时域多分辨分析方法的地闪雷电电磁脉冲计算

江志东 周璧华 刘亚文 杨 波

（解放军理工大学 电磁环境效应与电光工程国家级重点实验室，江苏 南京210007）

引 言

雷电是发生在大气中的一种瞬态大电流、高电压和强电磁辐射的天气现象.雷电电磁脉冲（Lightning Electromagnetic Pulse，LEMP）的计算对于架空电缆耦合评估、电气和电子设备防护以及雷电间接效应的研究至关重要.目前计算地闪放电回击通道辐射的LEMP有三类方法［1］，即精确解析法、近似法和数值计算法.其中时域有限差分（Finite Difference-Time Domain，FDTD）法具有大地电参数引入方便、一次计算可得到所有场点信息、得出的时域波形可直接用于耦合计算及便于编程实现等优点.自文献［2］首次将FDTD法引入到地闪放电回击通道几十米范围内LEMP的计算后，FDTD法广泛应用于地闪LEMP计算［3］、LEMP线缆耦合电压计算［4］、其他算法精度评估［5］等方面.

尽管FDTD法具有上述诸多优点，但由于数值色散和数值稳定性的影响，实际应用时易受计算机内存和速度的限制.如由于色散误差的限制，空间网格必须足够小，通常每个波长至少要取10个网格单元.由于稳定条件的限制，时间步长取值不能太大，计算时间势必增大.尽管当前计算平台发展迅速，计算效率仍是需要考虑的问题.

Krumpholz等［6］在1996年首次提出时域多分辨分析法（Multi-resolution time-domain，MRTD），该方法将矩量法（Moment of method，MoM）和多分辨分析（Multi-resolution analysis，MRA）结合来离散麦克斯韦方程组，在时域将电场与磁场分量分别展开成一系列空间上的尺度函数和时间上的脉冲函数之和.与FDTD法相比，MRTD法不仅具有更好的线性色散特性［7］，其最突出特点是对空间进行划分网格后每个波长采样两个点即可达到FDTD每个波长采10个点的精度，即Nyquist定理的极限，从而可以大大减少计算网格数，节省内存和计算时间.

为提高LEMP时域计算效率、减少内存消耗及克服经典FDTD法的数值色散问题，本文尝试将MRTD法引入到地闪LEMP的计算中，并与传统的FDTD法计算结果对比.理论和模拟实验结果表明，MRTD法在保持计算精度的前提下能够提高计算效率、节省计算资源.

1 基于MRTD的LEMP计算模型

MRTD算法从麦克斯韦方程组出发，将相应的场分量按选定的基函数展开，并将时间微分近似为中心差分，空间微分近似为空间点场值加权的平均，从而建立差分迭代方程.目前各种具有有限支撑域的小波尺度函数如Haar小波［8］、以及（Cohen Daubechies Feauveau，CDF）双正交小波［9］，Daubechies正交小波［10］等的MRTD算法已陆续被提出和应用于谐振腔、微带线和散射体的计算.

鉴于Daubechies正交小波尺度函数的紧支撑性和近似的移位内插特性，能够很好地平衡计算精度和计算复杂度之间的矛盾，本文选择Daubechies小波的尺度函数作为展开基.

根据矩量法和多分辨分析特性，将麦克斯韦旋度方程组中电场和磁场分量利用空间和时间基函数展开，以磁场分量Hz为例有如下展式

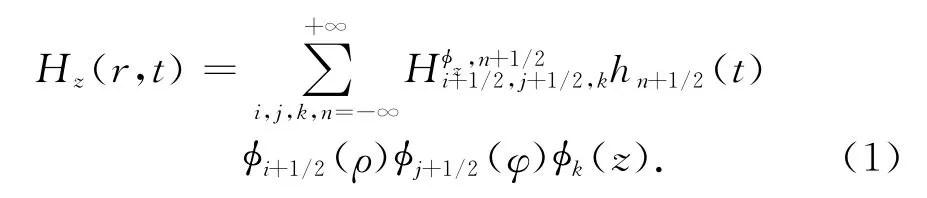
将磁场分量Hz的展开式即式（1）代入麦克斯韦旋度方程，并采用Galerkin采样方法［9］，得到场展开系数H1的MRTD迭代公式

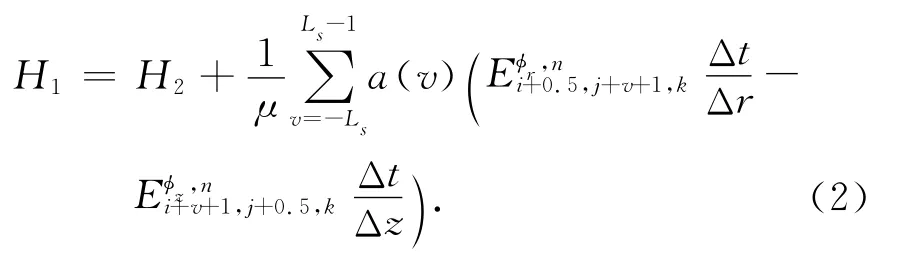
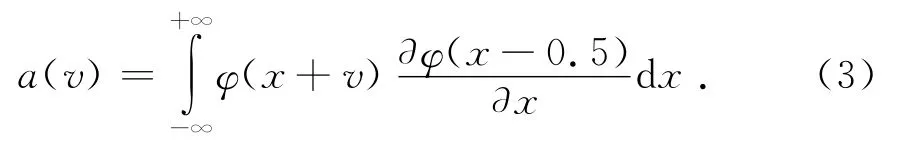
a（v）的值参考文献［11］，根据a（v）的对称关系a（-v-1）＝-a（v），只需要考虑0≤v≤2时的情形.

1.1 二维柱坐标下LEMP计算模型

近似认为地闪放电通道垂直于地面且四周围无穷空间，则地闪放电电流形成的场具有对称性，可在二维柱坐标系下求解，地闪放电通道附近的LEMP网格划分如图1所示.

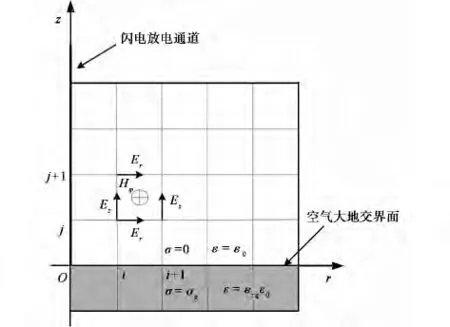
图1 二维柱坐标下MRTD计算域网格划分

二维柱坐标系下MRTD差分方程如下，其格式和FDTD类似，不同点在于任意时刻每个场点值由相应的展开系数和相邻场点值相乘后加权求得，即式（4）、（5）和（6）中的而展开系数的个数l与小波尺度函数的紧支撑性有关，本文采用的是db2，故LS为3.由此，得到基于Daubechies小波尺度函数的MRTD迭代公式：

式（4）、（5）和（6）中σ和ε分别表示自由空间或者大地中的电导率和介电常数，εrg为大地的相对介电常数.空气中σ＝0，ε＝ε0，大地中σ＝σg，εg＝ε0εrg.

1.2 激励源的引入及吸收边界处理

由于地闪回击电流位于二维柱坐标系中的z轴上，在图1的LEMP计算模型中，z轴上只有Ez一个分量，因此可以通过Ez在MRTD差分网格中引入激励源.

考虑到所计算问题的轴对称性，为减少计算量，只计算包含回击通道在内的半个剖面内的场，为此需要对轴线上的Ez作特殊处理.根据安培环路定理，在雷电流放电通道高度范围外不存在雷电流，在雷电放电通道高度范围内，采用如下差分格式

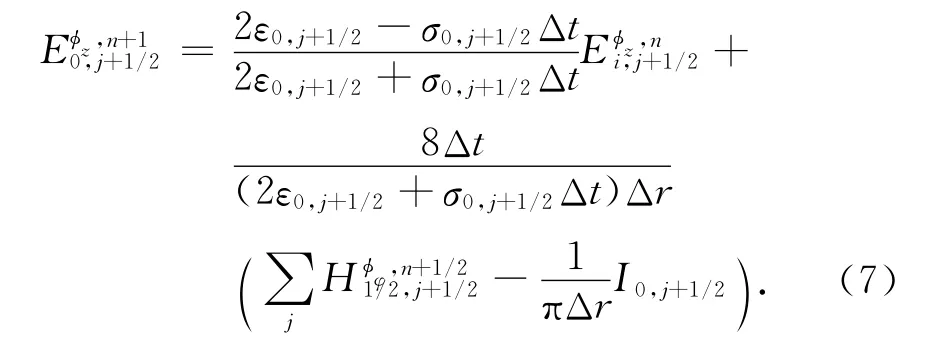
式（7）中，Ⅰ0，j＋1／2为距离地面高（j＋1／2）Δz处的电流元.

由于MRTD场展开方式的特殊性，需对特殊点进行处理.在计算空间某一点的电磁场分量系数时，关联系数a（v）决定了要考虑该分量周围电磁场系数的个数.由于基函数相互有重叠，导致边界条件复杂，设计满足特定应用的匹配层吸收边界是MRTD应用的一大难点.本文采用PML完全匹配层吸收边界，吸收层外侧采用PEC进行截断，并利用镜像原理对其进行处理.二维圆柱坐标情况下自由空间及有耗介质中PML内各场量的处理方式参见文献［12］.

2 数值仿真及分析

2.1 数值计算结果对比

数值计算采用的地闪回击通道模型为（modified transmission line model with linear current decay with height，MTLL）模型，回击通道高度设为7 200m，回击速度为1.1×108m／s.通道基电流表达采用双指数函数，分别选用1.2／50μs和0.25／100 μs波形作为首次回击和后续回击雷电流的典型波形.大地电参数σg＝0.001S／m，εrg＝10.计算空间3 600m×2 400m.

如图2所示，对于首次回击和后续回击LEMP的计算，FDTD法分别采用1m×1m和0.5m×0.5m的空间网格剖分，其计算的场分量作为标准参考值.MRTD法分别采用3m×3m和2m×2m的空间网格剖分，计算结果表明了MRTD法的有效性.同时，不同网格剖分对于垂直电场的影响不大，水平电场随着网格的变大，在波形的初始阶段和峰值处出现一定程度的振荡.由于水平电场易受大地电参数的影响，计算空间网格的增大使得大地电参数对计算结果的影响更加明显.

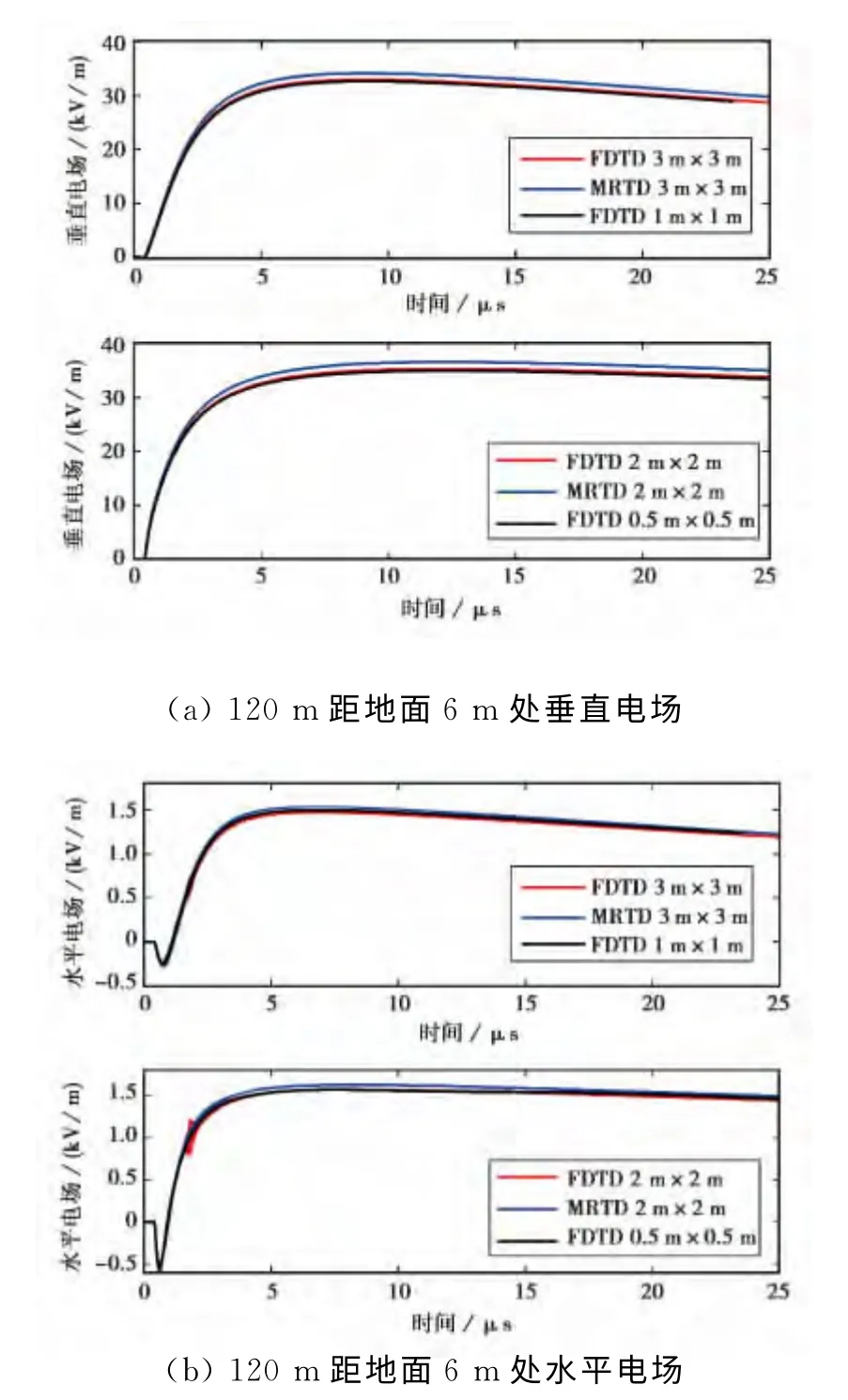
图2 距回击通道120m处垂直电场和水平电场

如图3所示，与图2结果类似，不同的空间网格剖分对垂直电场分量的计算结果没有影响.水平电场分量的计算结果整体保持一致，随着网格的变大出现一定程度的振荡.

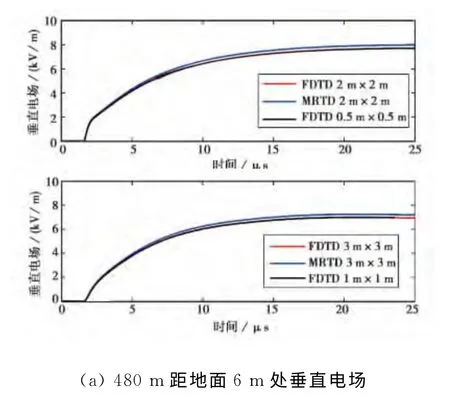
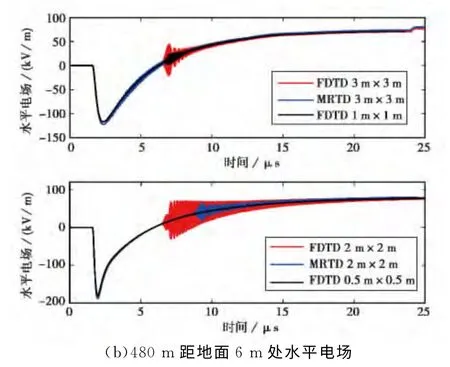
图3 距回击通道480m处垂直电场和水平电场

2.2 讨论与分析

为分析MRTD算法中差分近似后的数值色散特性，采用类似于FDTD的分析方法，将平面波方程带入MRTD迭代方程，得到差分近似后相速和光速之比的各项异性的关系，如图4所示.

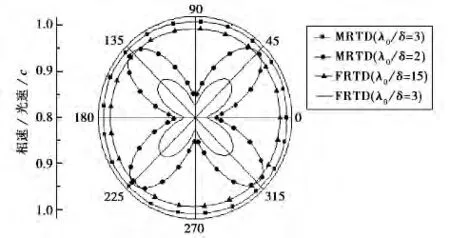
图4 差分近似后相速和光速之比的各项异性

图4中λ0／δ为单个波长内的采样点数，当λ0／δ为参变量时，从图中相速和光速之比vφ／c与平面波传播方向角φ之间的关系可以看出，MRTD算法单个波长内采样点取3时的各项异性程度优于FDTDF法采样点为15时的情形，故MRTD法在取较大网格时仍然能够保持较高的精度和较低的数值色散误差.

3 结 论

本文将MRTD算法引入地闪LEMP的计算，选用Daubechies小波尺度函数作为基函数，采用MTLL地闪回击模型在二维柱坐标系下计算了地闪放电通道不同距离处LEMP场分量.数值仿真结果证实了MRTD算法的有效性，与FDTD算法相比，在保证计算精度的前提下，采用较大计算空间网格，减少计算机内存开销.目前，采用MRTD法的主要难点在于，无论如何选择展开基底，其时间稳定性条件比FDTD法都要苛刻.此外，虽然MRTD算法计算大目标时能够以几何级数的量级节省内存，但由于基函数互相有重叠，导致边界条件复杂化，设计满足特定应用的匹配吸收边界是另一难点.下一步可考虑优化吸收边界匹配层的设计，以便将MRTD法更好的应用于地闪LEMP数值分析、线缆耦合研究等相关领域.

［1］RAKOV V A，RACHIDI F.Overview of recent progress in lightning research and lightning protection［J］.IEEE Trans Electromagn Compat，2009，51（3）：428-442.

［2］YANG Chunshan，ZHOU Bihua.Calculation methods of electromagnetic fields very close to lightning［J］.IEEE Trans Electromagn Compat，2004，46（1）：133-141.

［3］杨 波，周璧华，孟 鑫.地闪雷电电磁脉冲在大地中的分布研究［J］.物理学报，2010，59（12）：8978-8985.YANG Bo，ZHOU Bihua，MENG Xin.Distribution of cloud-to-ground lightning electromagnetic pulse fields under the ground［J］.Acta Physica Sinica，2010，59（12）：8978-8985.（in Chinese）

［4］YANG Bo，ZHOU Bihua，CHEN Bin，et al.Numerical study of lightning-induced currents on buried cables and shield wire protection method［J］.IEEE Trans Electromagn Compat，2012，54（2）：323-331.

［5］ZHANG Qilin，LI Dongshuai，Zhang Yuanyuan，et al.On the accuracy of wait＇s formula along a mixed propagation path within 1km from the lightning channel［J］.IEEE Trans Electromagn Compat，2012，54（5）：1042-1047.

［6］KRUMPHOLZ M，KATEHI L P B.MRTD：new time-domain schemes based on multiresolution analysis［J］.IEEE Transactions on Microwave Theory and Techniques，1996，44（4）：555-571.

［7］代少玉，吴振森，徐仰彬.用基于Daubechies尺度函数的时域多分辨分析计算电磁散射［J］.物理学报，2007，56（2）：786-790.DAI Shaoyu，WU Zhensen，XU Yangbin.Using the MRTD based on Daubechies scaling function to solve the problem of electromagnetic scattering［J］.Acta Physica Sinica，2007，56（2）：786-790.（in Chinese）

［8］FUJII M，HOEFER W J R.Multiresolution analysis similar to the FDTD method-derivation and application［J］.IEEE Transactions on Microwave Theory and Techniques，1998，46（12）：2463-2475.

［9］CHEONG Y W，LEE Y M，RA K H，et al.Wavelet-Galerkin scheme of time-dependent inhomogeneous electromagnetic problems［J］.IEEE Microwave Guid Wave Lett，1999，9（8）：297-299.

［10］KOVVALI N，LIN W，CARIN D L.Order of accuracy analysis for multiresolution time-domain using Daubechies bases［J］.Microw Opt Technol Lett，2005，45（4）：290-293.

［11］高强业，周建江，曹群生.MRTD方法的色散特性分析和电磁散射应用［J］.南京航空航天大学学报，

2010，42（2）：191-197. GAO Qiangye，ZHOU Jianjiang，CAO Qunsheng.Dispersion property analysis and electromagnetic scattering application for MRTD Method［J］.Journal of Nanjing University of Aeronautics ＆Astronautics，2010，42（2）：191-197.（in Chinese）［12］LIU Yawen，CHEN Yiwang，CHEN Bin，et al.A cylindrical MRTD algorithm with PML and Quasi-PML［J］.IEEE Transactions on Microwave Theory and Techniques，2013，61（3）：1006-1017.