雷达目标微多普勒特征提取的频率稳定度约束

鄢宏华 王文生

（中国电子科学研究院，北京100041）

引 言

一般地，将目标或目标部件除质心平动以外的振动、转动和加速运动等微小运动统称为微动［1］.微动在自然界普遍存在，如行人手和腿的摆动、心跳、桥梁的振动、车轮的滚动以及中段弹头的进动等.微动会在雷达回波中引入时变的、周期性的频率调制，文献［1］称之为微多普勒效应.微多普勒是研究目标微动特性的一种有效途径，它能反映目标独特、精细的运动特征，微多普勒特征的成功提取可用于雷达目标识别［2-4］.

关于微多普勒特征的提取方法，已有众多文献对其进行研究，但到目前为止，还没有文献来定量分析雷达频率源相位噪声对微多普勒特征提取的影响.而在工程实践中，相位噪声很可能是微多普勒特征提取的主要限制因素之一，因为目标的微动幅度常常是比较微弱的，如心跳、卡车的振动、弹道导弹的进动等.为了能够检测这类精细运动，就要求发射信号具有较高的载频，频率越高，良好相位噪声性能就越难实现；其次，为了提取微多普勒特征，常采用时频分析处理，得到的是回波信号能量在时间、频率两维的分布，这与时间或频率的单维处理不一样，其对相位噪声的性能要求更高；第三，也是常容易被忽视的一点，那就是由于相干检波的存在，远、近距离目标的微多普勒特征提取对相位噪声的要求是有很大差别的，可查阅文献中的微多普勒特征提取实验的目标距离都很近［5-6］，那么由于相干检波效应的存在，其对相位噪声性能要求不高（在后面的仿真实验中可以看到），但在导弹防御场合，如对几千千米外的弹道目标进行微多普勒特征提取，那么其对频率源稳定度的要求与暗室实验是有很大区别的.因此，有必要就雷达频率源相位噪声对微多普勒特征提取的影响进行研究，并给出现有的晶振水平能否有效支撑微波雷达对中段弹头目标微多普勒特征提取的结论.

1 频率源相位噪声模型

振荡器的瞬时输出电压可简化表示为

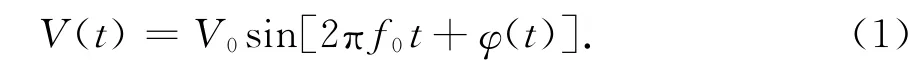
式中：V0为标称幅度；f0为标称频率；φ（t）表示瞬时相位起伏即相位噪声.

在频域，高稳晶振相位噪声可用下面的单边功率谱密度模型来描述为

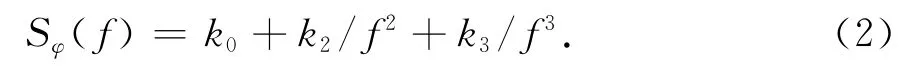
式中：k0代表调相白噪声；k2／f2代表调频白噪声；k3／f3代表调频闪烁噪声.

式（2）被文献［7-8］所采用，因此，无一例外的，本文也采用这一相位噪声模型来表示实际雷达频率源的相位噪声，其单边功率谱密度由斜率特性不同的三段所组成，如图1所示.

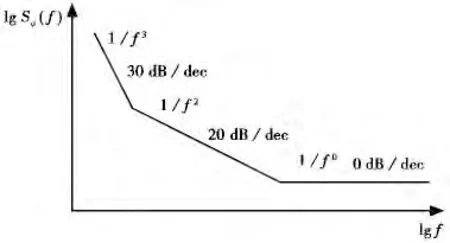
图1 高稳晶振典型相位噪声模型

2 幂律噪声产生与相位噪声综合

2.1 幂律噪声产生

2.1.1 调频白噪声产生

1／f2噪声的产生比较简单，让白噪声序列通过传递函数为

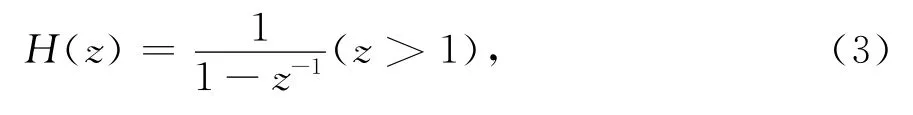
对应的差分方程为

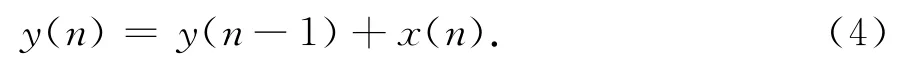
如果要设定1／f2噪声的幂律起始点为fk，那么可将上述滤波器修改为如下的一阶低通滤波器为

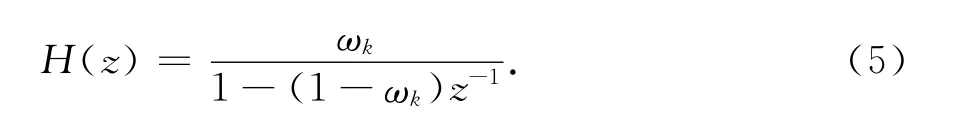
式中：ωk＝2πfk／fs，fs为信号采样率.

2.1.2 调频闪烁噪声产生

对于1／f3噪声，本文参考文献［9］利用并联一阶低通滤波器组产生1／f噪声的原理，给出如图2所示的并联二阶低通滤波器组来产生1／f3噪声.fc1～fcN为所期望的幂律噪声频率范围，现将其分成N-1段，fc1，fc2，…，fcN称为每个低通滤波器的转角频率（低通截止频率）.

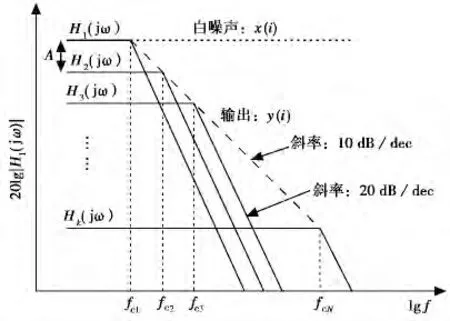
图2 并联二阶低通滤波器组合成调频闪烁噪声原理图

从图2中几何关系可得如下两式：

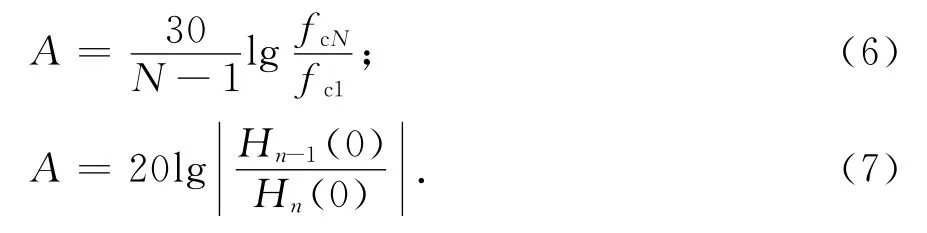
所以相邻滤波器的直流增益比由如下式子表示为

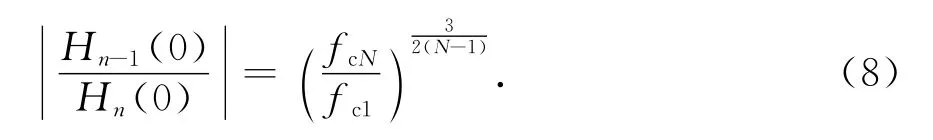
因此，图2中所有的二阶低通滤波器可表示为

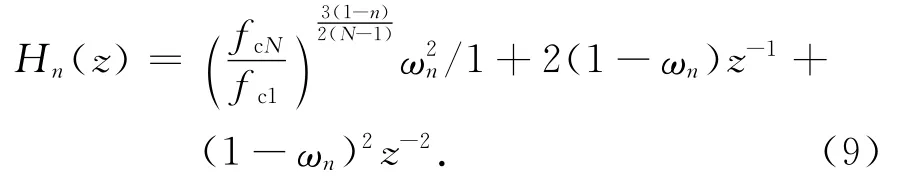
式中：n＝1，2，…，N；ωn＝2πfcn／fs.式（9）中的第一项是由不同滤波器的增益比造成的，后一项表示的是6dB截止频率为ωn的二阶低通滤波器，其在ω＞ωn处的频率响应以40dB／dec的速率滚降，但并联低通滤波器组合成的频率响应近似具有30 dB／dec的衰减特性.

2.2 频率源相位噪声综合

高稳晶振的相位噪声单边功率谱密度由式（2）给出，现重写如下：

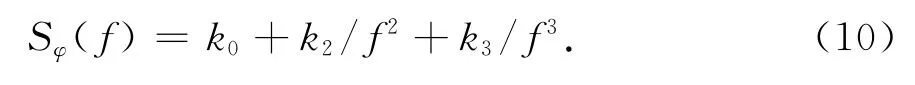
为综合出符合上述功率谱特性的相位噪声序列，可由上述的幂律噪声产生方法，采用如图3所示的参数化时域模型来实现，该相位噪声综合方法具有如下两优点：

1）通过设定低通滤波器的转角频率（截止频率）可以方便改变特定幂律噪声的频率范围，即幂律噪声频率范围参数化；

2）通过功率因子ρn配合相应的滤波器传递函数H（jω）可以方便设定相位噪声在特定频率处的功率谱密度值，即相位噪声谱密度大小参数化.

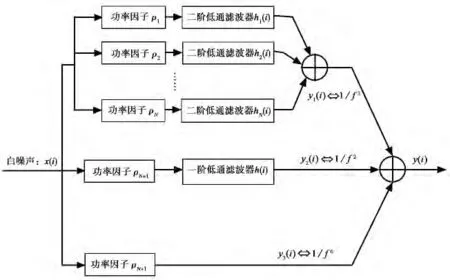
图3 频率源相位噪声综合模型

为验证图3模型综合出的相位噪声效果，现进行如下仿真实验：设定幂律噪声范围为1Hz～1 MHz，在1～100Hz频率范围内是f-3噪声，在100 Hz～1kHz频率范围内是f-2噪声，在1kHz～1 MHz频率范围内是f0噪声，要求在1kHz处的单边功率谱密度为-75dB，那么由幂律谱特性可知在100Hz处的单边功率谱密度为-55dB.

由于f-3噪声跨越两个十倍频程，那么使用4个式（9）所定义的并联二阶低通滤波器就可以得到所期望的功率谱密度衰减特性；对于f-2噪声，让一定功率的白噪声通过式（5）所示的一阶低通滤波器就可以了，在时域采样率fs＝2MHz下，按照图3模型综合出的相位噪声单边功率谱密度如图4所示.其中绿点划线代表的是本仿真实验设定的相位噪声的理论模型，红实线代表的是基于图3相位噪声综合模型频率响应的功率谱密度计算值.由图可知，在整个输出频率范围内，基于模型频率响应计算值的其谱密度衰减特性是沿着理论曲线渐变的，从-30 dB／dec到-20dB／dec，再到0dB／dec.因此，相位噪声综合模型具有所期望的频率响应特性，验证了本文所提相位噪声综合方法的理论可行性，而且在数值上也非常精确.

上述分析结果是基于理想白噪声的，下面利用最小二乘法对实际滤波输出的功率谱密度进行数字刻画.在1～100Hz范围内，将谱密度及频率的对数值进行直线拟合后，得到斜率及常数值分别为-2.98、4.4dB，与理论斜率及常数值-3、4.4dB的相对误差分别为0.7%、12%；在100Hz～1kHz范围内，得到拟合的斜率及常数值分别为-1.94、15.3dB，与理论斜率及常数值-2、15dB的相对误差分别为3%、2%；在1～1MHz范围内，得到拟合的斜率及常数值分别为-0.005、75.2dB，与理论斜率及常数值0、75dB的相对误差均很小.因此，利用图3的相位噪声综合模型对白噪声序列滤波可以有效模拟载频信号相位噪声.

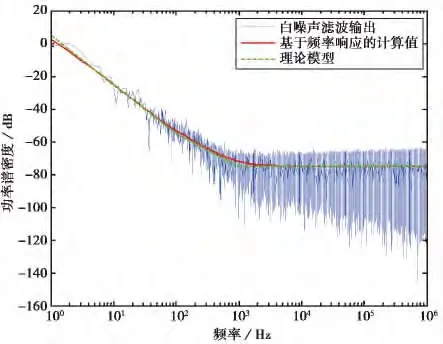
图4 综合输出相位噪声单边功率谱密度

3 相位噪声对微多普勒特征提取影响分析

在现代全相干雷达系统中，稳定的本机振荡器、发射信号、相干振荡器、全机时钟等都是通过频率合成器产生，频率合成器的频率基准通常来自于一个高稳晶振，因此高稳晶振的非理想频率特性对微多普勒特征提取的影响是多方面的，如导致脉冲重复频率抖动、模数转换器采样时钟抖动等，但不管怎样，载频信号中存在的相位噪声是影响微多普勒特征提取的主要因素，这就是为什么稳定本振在雷达接收机中具有重要地位的原因.因为，对于具有一定频率稳定度的频率源，其相位噪声功率谱密度与倍频次数m之间的关系为20lgm［9］.

为简化分析，可假设雷达发射如下单载频脉冲信号为

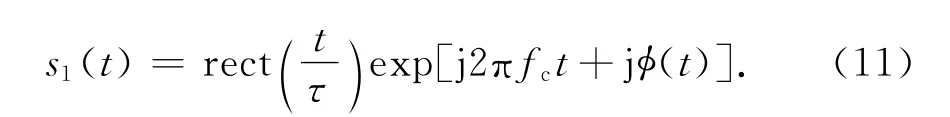
式中：τ表示发射脉冲宽度；fc为发射信号载频；φ（t）表示载频信号的相位噪声.

做单一微运动的理想散射点其径向运动可简单表示为

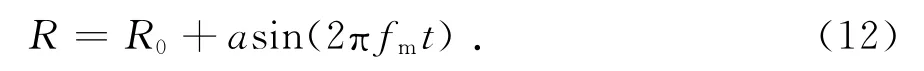
式中：R0表示目标初始距离；a为散射点微动幅度；fm为微动频率.那么可得该散射点回波信号为

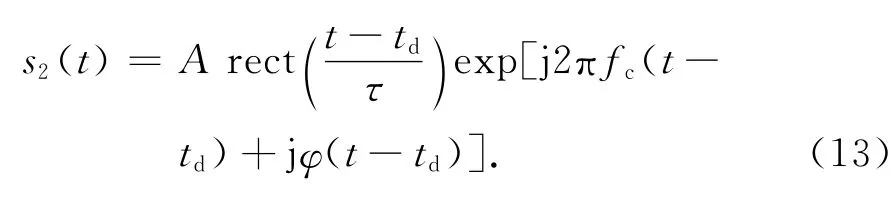
式中：A为散射点后向散射系数；td＝2R／c为微动散射点回波延迟.

若不计功率放大链引入的额外相位噪声，那么经混频处理后的基带信号为

式中：第一个相位项包含着目标微动信息，是提取目标微多普勒特征所需要的；第二个相位项是噪声项，它对微多普勒特征提取起干扰作用.

令

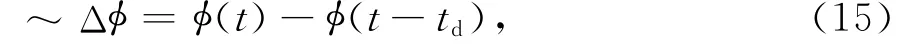
将Δφ称为基带回波信号相位噪声.若将φ（t）对应的发射信号相位噪声谱密度记为Sφ（f），那么Δφ对应的基带回波信号相位噪声谱密度SΔφ（f）为

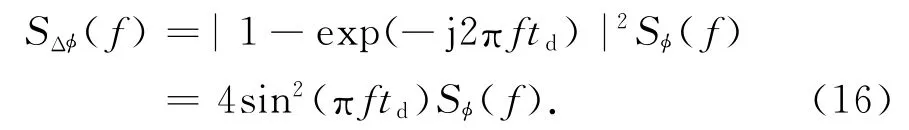
可见，基带回波信号相位噪声不等于发射信号相位噪声，其谱密度受4sin2（πftd）的调制，结合Sφ（f）的幂律谱特性可得如下结论：

1）相干检波可以削弱相位噪声中的低频成分对微多普勒特征提取的影响；

2）频率源相位噪声对微多普勒特征提取的影响还与目标距离有关，当目标距离很近时（暗室测试），相干检波可以大大降低微多普勒特征提取对频率稳定度的要求.

4 仿真实验研究

为进一步研究频率源相位噪声对微多普勒特征提取的影响，还需建立一套仿真实验系统并给出一种定量分析方法.图5就是一套完整的仿真实验系统，主要功能模块包括仿真参数设置、基带回波相位噪声生成、基带脉间回波序列生成以及微多普勒特征提取.为了定量刻画频率源相位噪声对微多普勒特征提取的影响，在此引入基于逆Radon变换的分析方法.关于逆Radon变换在微多普勒特征提取中的应用，由于篇幅所限在此不再赘述，具体内容请参阅文献［10］.

默认仿真实验参数设置如下：发射信号载频fc＝10GHz，散射点微动幅度a＝0.15m，微动频率fm＝0.45Hz，脉冲重复频率fPR＝200Hz，中频信号采样率fs＝2MHz，目标距离R0＝2 000km，相位噪声的参数设置同2.2节.

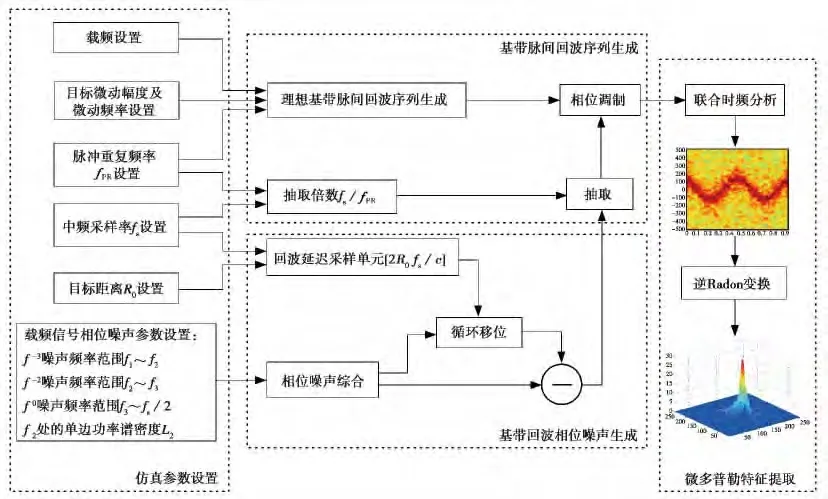
图5 相位噪声对微多普勒特征提取影响的仿真系统

综合出的载频信号相位噪声单边功率谱密度如图4所示，其时间序列如图6（a）所示，图6（b）、（c）、（d）显示了全相参雷达的相干检波效应.可以看到，相干检波操作有效抑制了低频相位噪声，而且目标的基带回波相位噪声强度随雷达威力的增大而增大.

对于脉冲雷达，对目标的微多普勒特征提取是基于同一距离单元的脉间回波序列的.因此，为了研究频率源相位噪声对微多普勒特征提取的影响，应当对相干检波后的相位噪声序列进行fs／fPR倍抽取，利用抽取后的脉间相位噪声对理想的微动目标回波进行相位调制，就得到了受相位噪声污染的基带脉间回波序列，对其采用时频分析以及逆Radon变换处理，以此来研究相位噪声对目标微多普勒特征提取的影响.

4.1 相位噪声大小对微多普勒特征提取的影响

当1kHz处的相位噪声单边功率谱密度为默认设置的-75dB时（如利用工程实践中常用的单边带相位噪声来表示，那就是-78dBc／Hz＠1 kHz），目标回波的时频分析结果如图7（b）所示，可以看到，在微多普勒特征曲线（微动时频像）周围出现了明显的噪声干扰，若以峰值检测法［11］提取目标微动的瞬时频率，那么在某些时刻将会出现错误的瞬时频率估计；当将相位噪声设置为-73dBc／Hz＠1kHz时，微动时频像被进一步破坏（图7（c）），在大部分时间内，目标的瞬时频率都被改变了；如果继续恶化载频信号相位噪声性能，将其设置为-68 dBc／Hz＠1kHz，那么目标的微动时频像就被完全破坏了（图7（d））.

为了定量刻画相位噪声对微多普勒特征提取的影响，对上述时频分析结果进行逆Radon变换［10］，受基带脉间相位噪声污染的微动时频像逆Radon变换值与理想频率源下微动时频像逆Radon变换值之间的对比可以用来定量刻画相位噪声对目标微多普勒特征提取的影响.时频分析结果的逆Radon变换如图8所示（各图中的幅值都利用理想频率源下的逆Radon变换峰值进行归一化处理），由图可见：当相位噪声设置为-68dBc／Hz＠1kHz，在逆Radon域几乎不存在微动时频像所对应的峰值点；当相位噪声设置为-73dBc／Hz＠1kHz，逆Radon变换峰值点位置与理想频率源下的相同（此时可以正确估计微多普勒特征曲线参数），但在相位噪声干扰下，目标回波能量没能得到有效积累，峰值幅度损失严重，达到了2.8dB，即使将相位噪声性能提高到-78dBc／Hz＠1kHz，目标回波能量也存在比较严重的损失，为0.9dB.

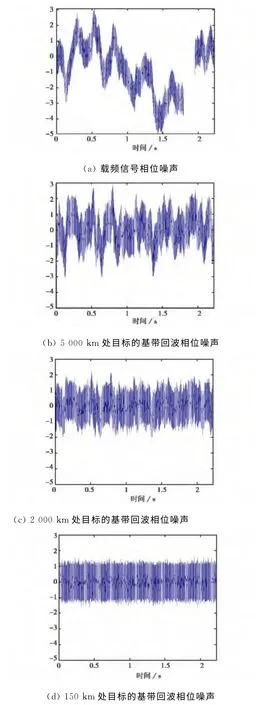
图6 载频信号相位噪声的相干检波效应

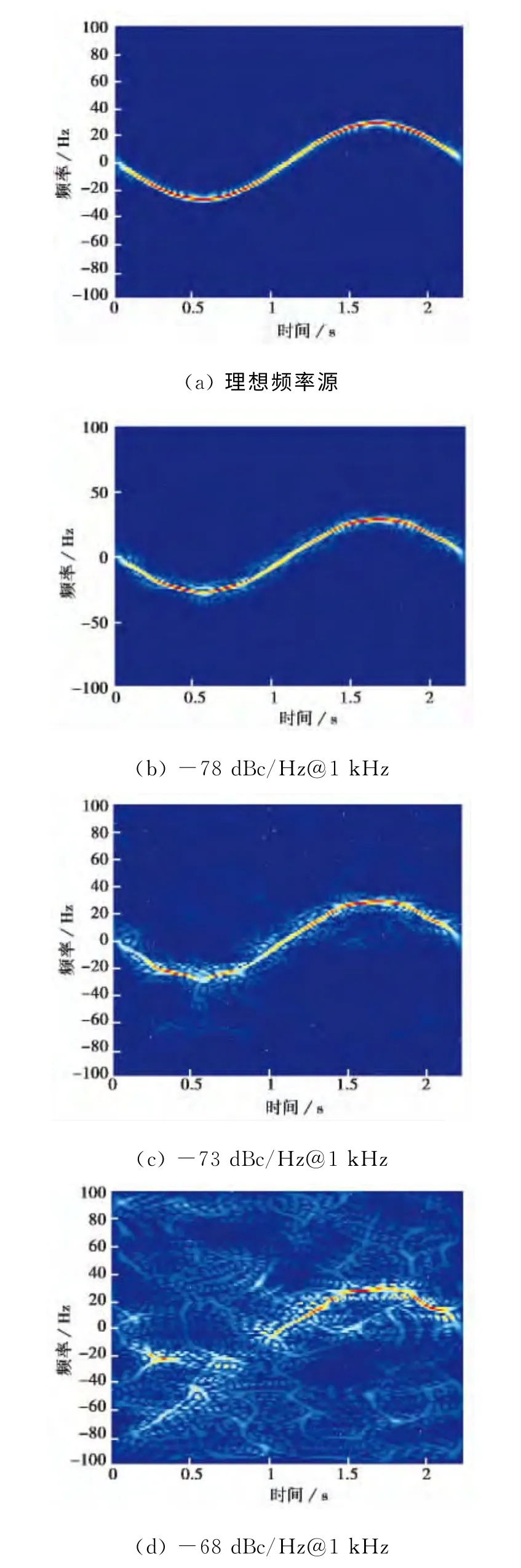
图7 受不同程度相位噪声污染的目标微动时频像提取

4.2 目标距离远近对微多普勒特征提取的影响

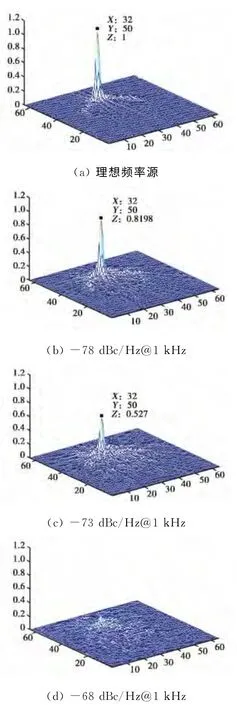
图8 受不同程度相位噪声污染的微动时频像的逆Radon变换.

由前面的分析已知，同一载频信号相位噪声对不同距离目标的微多普勒特征提取影响是不同的，当相位噪声大小为默认设置的-78dBc／Hz＠1 kHz，目标距离分别为150km、2 000km、5 000km时，微动时频像提取结果如图9（b）、（c）、（d）所示，图10（b）、（c）、（d）显示了各种距离下时频分析结果的逆Radon变换.在目标距离为5 000km时，目标峰值幅度损失严重，达2.4dB；在目标距离为2 000 km时，目标峰值幅度损失为0.9dB；而当目标距离为150km时，目标峰值幅度损失又进一步减小，为0.4dB.

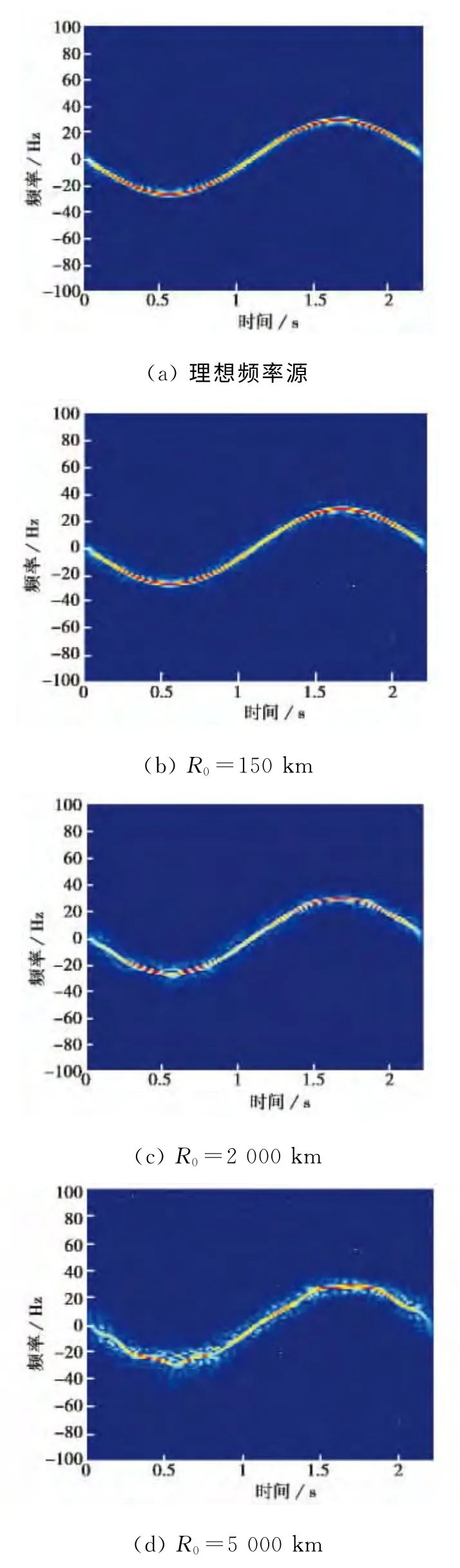
图9 相同载频信号相位噪声对不同距离目标的微动时频像提取影响

4.3 仿真实验总结

通过上述仿真实验可得如下结论：

1）相干检波操作可大大抑制低频相位噪声对目标微多普勒特征提取的影响；

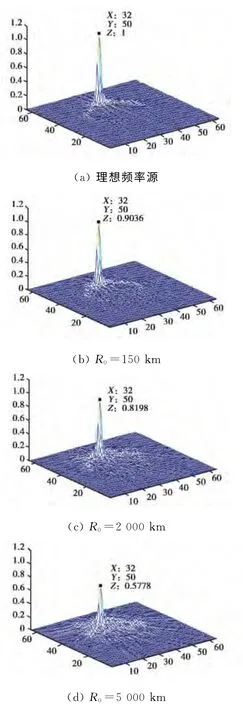
图10 不同距离目标的微动时频像的逆Radon变换

2）近距离目标相对远距离目标允许更差的频率稳定度指标，考虑到回波信噪比随着目标距离增大而严重下降（与R40成反比）这个因素，实际工程中对远距离目标的微多普勒特征提取要比微波暗室测量困难得多；

3）对于微多普勒特征在中段弹道导弹防御中的应用，以目标距离2 000km为例，由仿真实验可知，在回波能量积累损失为0.9dB时，载频信号的相位噪声指标为-78dBc／Hz＠1kHz，若要使回波能量积累损失在0.5dB以内，那么载频信号相位噪声性能要在-80dBc／Hz＠1kHz以上.如果雷达发射信号载频为10GHz，且载频信号由标称频率为10MHz的基准晶振经直接倍频方式得到，那么微多普勒特征提取对基准晶振的相位噪声性能约束为-140dBc／Hz＠1kHz；如果雷达载频为5GHz，那么对基准晶振的相位噪声性能要求就可以相应降低，为-134dBc／Hz＠1kHz，但此时目标的微多普勒幅度就只有载频为10GHz时的一半，这又不利于目标的微动检测和测量.因此，实际工程实践中，应该根据目标微动的先验知识，结合基准晶振所具有的频率稳定度来综合考虑雷达工作频率的选择，所选取的雷达载频既要保证让微动目标具有较大的微多普勒幅度以利于微动检测和测量，同时又不至于引入过大的相位噪声而严重干扰目标的微多普勒特征提取.

查阅资料［12］可知，对于标称频率为10MHz的低相位噪声晶振，其相位噪声性能可达到-150～-160dBc／Hz＠1kHz，因此，从相位噪声指标上来说，现有的晶振水平可用于微波雷达对弹头目标的微多普勒特征提取.

5 结 论

频率源相位噪声是实际工程应用中限制雷达目标微多普勒特征提取的主要因素之一，是微动测量雷达研制中载频选择的一个重要考虑因素.本文给出的参数化模型能够对频率源相位噪声进行精确模拟，可作为独立模块应用于其他类型雷达的频率稳定度约束研究；建立的仿真实验系统可为弹道导弹防御中微动测量雷达的基准晶振选择提供一定指导.

［1］CHEN V C，LI F，HO S S，et al.Micro-Doppler effect in radar：phenomenon，model and simulation study［J］.IEEE Transactions on Aerospace and Electronic Systems，2006，42（1）：2-21.

［2］高红卫，谢良贵，文树梁，等.基于微多普勒特征的真假目标雷达识别研究［J］.电波科学学报学报，2008，23（4）：775-780.GAO Hongwei，XIE Lianggui，WEN Shuliang，et al.Research on radar target identification of warhead and decoys based on micro-Doppler signature［J］.Chinese journal of radio science，2008，23（4）：775-780.（in Chinese）

［3］关永胜，左群声，刘宏伟.基于微多普勒特征的空间锥体目标识别［J］.电波科学学报学报，2011，26（2）：209-215.GUAN Yongsheng，ZUO Qunsheng，LIU Hongwei.Space cone target identification based on micro-Doppler signature［J］.Chinese Journal of Radio Science，2011，26（2）：209-215.（in Chinese）

［4］贾守卿，江小敏，夏明耀.基于微多普勒特征的目标分类［J］.电波科学学报学报，2013，28（3）：443-448.JIA Shouqing，JIANG Xiaomin，XIA Mingyao.Target classification based on micro-Doppler signature［J］.Chinese Journal of Radio Science，2013，28（3）：443-448.（in Chinese）

［5］CAI C J，LIU W X，FU J S，et al.Radar micro-Doppler signature analysis with HHT［J］.IEEE Transactions on Aerospace and Electronic Systems，2010，46（2）：929-938.

［6］刘 进.微动目标雷达信号参数估计与物理特征提取［D］.长沙：国防科学技术大学，2010.LIU Jin.Radar Signal Parameter Estimation and Physical Feature Extraction of Micro-motion Targets［D］.Changsha：National University of Defense Technology，2010.（in Chinese）

［7］赵声衡，赵 英.晶体振荡器［M］.北京：科学出版社，2008.

［8］STASZEWSKI R B，FERNANDO C，BALSARA P T.Event-driven Simulation and modeling of phase noise of an RF oscillator［J］.IEEE Transaction on Circuits and Systems，2005，52（4）：723-733.

［9］弋 稳.雷达接收机技术［M］.北京：电子工业出版社，2006.

［10］鄢宏华，傅雄军，栗 苹，等.基于逆Radon变换的多散射点微动检测与测量［J］.北京理工大学学报，2012，32（5）：526-530.YAN Honghua，FU Xiongjun，LI Ping，et al.Detection and measurement to multiple scatterers with micro-motion based on inverse radon transform［J］.Journal of Beijing Institute of Technology，2012，32（5）：526-530.（in Chinese）

［11］陈行勇，刘永祥，黎 湘，等.雷达目标微多普勒特征提取［J］.信号处理，2007，23（2）：222-226.CHEN Hangyong，LIU Yongxiang，LI Xiang，et al.Eatraction of micro-Doppler signatures for radar target［J］.Signal Processing，2007，23（2）：222-226.（in Chinese）

［12］石家庄博亚电子科技有限公司：http：／／www.boyasky.com／default.asp［OL］，2013.Shijiazhuang Boya Electronic Technology Corporation：http：／／www.boya-sky.com／default.asp［OL］，2013.