固定单站纯方位目标运动参数的解析方法

郁 涛

（上海微波设备研究所，上海201802）

引 言

在被动测量的情况下，仅仅利用目标的方位信息，估计目标运动参数的过程，称为纯方位目标运动分析.对运动目标的纯方位观测是一个经典问题，至今为止的研究结果是，在二维平面上，当目标不是在相对于单观测站的径向方向运动时，利用静止单观测站所测量到的匀速直线运动目标的方位以及时差，仅可以估计出目标的航向角、目标通过航路勾径点的时刻、以及速度与初距的比值［1-2］.

现有的包含移动时差的纯方位目标运动分析之所以得不到完整的定位解，其原因在于仅利用了距离与速度之间的关系.事实上，在现有的纯方位目标运动分析中是可以包含有目标移动时差参量的，固定单站还可以依据观察时差建立自时差测量方程.

采用最小二乘法能实现目标定位［3-6］，但这不是本文所探讨的方法，本文基于几何和时差约束条件研究了纯方位观测的解析方法.首先利用自时差方程和几何关系证明目标端相邻移动距离之比近似等于观测处相邻观测时差之比；然后，再次利用前置角与观测方位角之间的几何关系解出目标端的前置角和航向角；随后的分析表明，一旦利用三角函数关系直接解算得到相邻移动距离的比值，并通过一次迭代计算再次求得准确度更高的前置角，则即可直接从自时差方程准确的求得移动目标的各个运动参数.

1 自时差测量方程

固定单站与被测目标间的几何关系如图1所示，在短时间内，目标可被假定为近似匀速直线运动，固定观测单站连续观测目标的方位角，同时，测量两次测向之间的时差值.

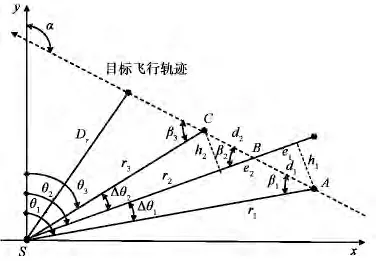
图1 固定单站无源定位几何模型

假定目标信号在位置A时的发射瞬间的时间值为T0，则观测站所接收到的此来波信号的时间值T1为

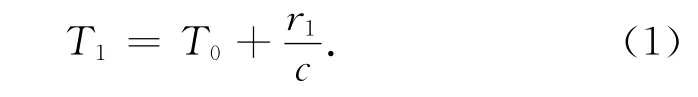
式中：r1是目标与探测站之间的径向距离；c是波的传播速度.

当目标移动到达位置B时，分段考虑信号传播和目标移动所花费的时间，固定观测站所接收到的来自位置A处，且从T0时刻算起的时间累加值T2为

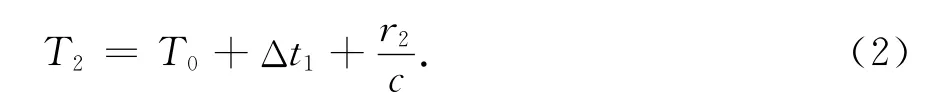
式中：r2是目标在位置B处的径向距离；Δt1＝d1／v为目标从A移动到B的时间间隔，v是目标的移动速度.

两观测时间之差为

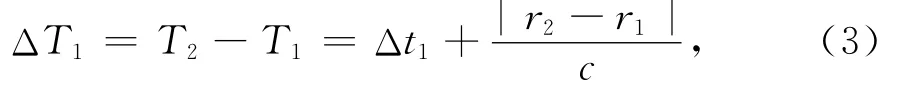
按同样的方法有

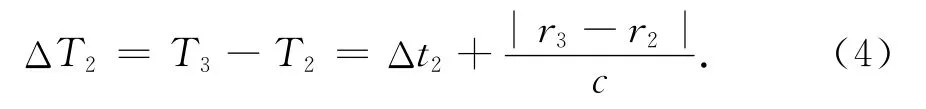
式中：Δt2＝d2／v为目标从B移动到C的时间间隔.

因自时差是目标移动时间与电波在路程差上的移动时间之和，为满足物理观察的真实性和计算公式的普遍适用性，对程差加绝对值符号是必须的.否则，一旦目标的移动航向改变，路程之差就有可能出现负值，此时，对分段移动时间间隔的累加行为将无法得以保持.

对观测时差移项整理后得：

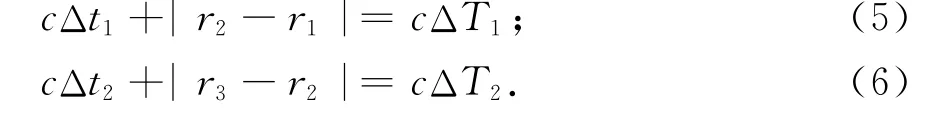
2 移动距离与观测时差间的比值

根据图1所示的几何关系，可以得到方位的相邻角度差Δθi为

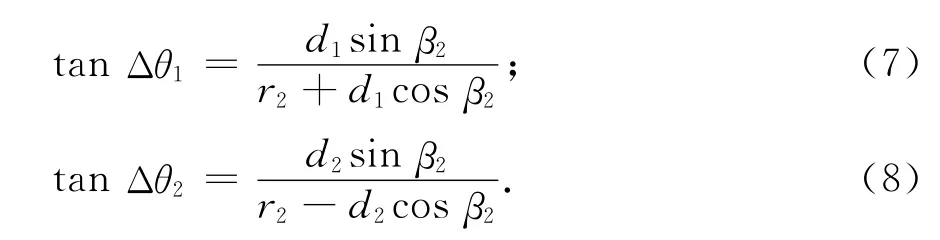
式中：di是目标在Δti时间内的移动距离；βi是目标的前置角；角度差Δθi＝θi＋1-θi，可通过纯方位检测获得，θi是在探测站位置处所测量得到的目标方位角.

通过变形整理，且两式联解消去径向距离r2之后，可得到相邻移动距离的比值为

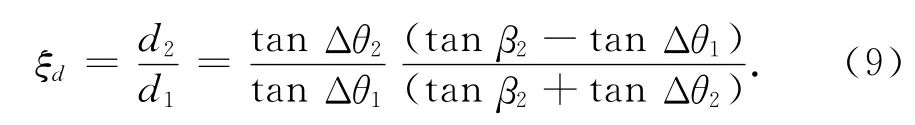
若前置角未知，则目标相邻移动距离的比值是不能被确定的，但由图1所示的几何关系还可得到：

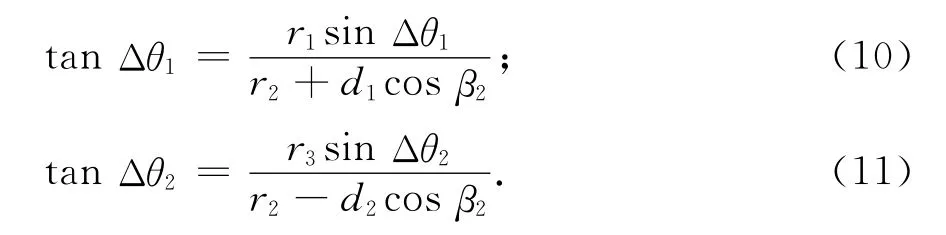
当Δθi较小时，近似有tanΔθi≈sinΔθi，等式两边相约后可得到：

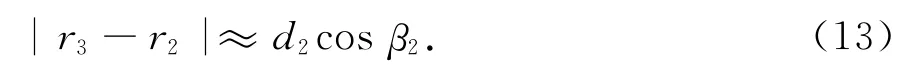
将上述关系代入时差方程式（5）和（6），并将式中的移动时间间隔用移动距离与移动速度的比值置换，得：

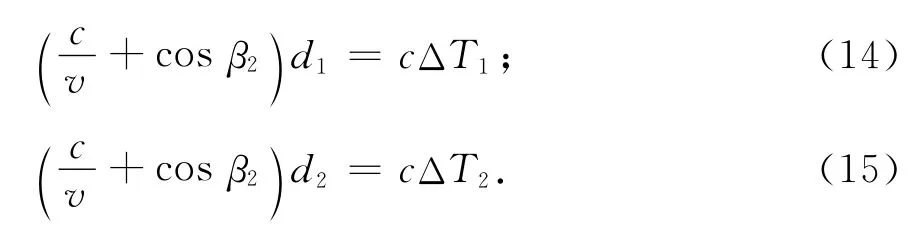
由上述的两式之比即可得到在目标相邻移动距离之比与观测站相邻时差之比之间的一个近似关系式

事实上，在匀速飞行的情况下，因di＝vΔti，故有

即近似有恒等式

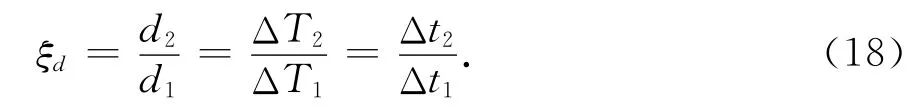
由于观测时间差ΔTi可通过测量获得，故移动距离之比可被近似确定.

3 目标的前置角和航向角

3.1 计算公式

一旦将移动距离与观测时差间的比值关系式（16）代入相邻飞行距离的比值关系式（9），则即可解出目标的前置角

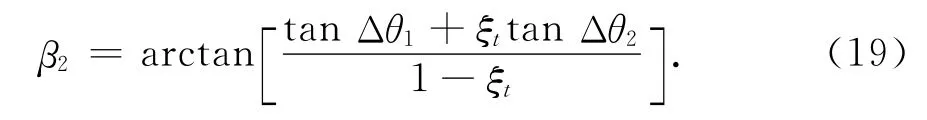
由内外角关系α＝θi＋βi，可解出航向角

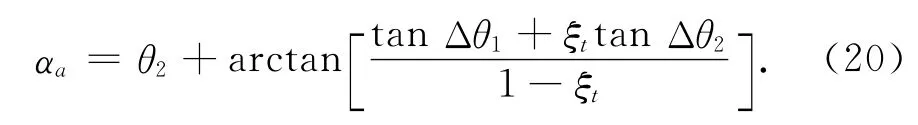
3.2 相对计算误差

图2给出了当前置角在第一象限内变化时，对于不同的起始测量方位角，航向角的真实值α与计算值αa间的相对误差比对，其计算式为

模拟计算证明，航向角的解析计算结果是相当准确的，且方位起始角越大，计算的准确性越好.

3.3 象限范围

模拟计算表明航向角计算式（20）仅适用于在0°＜β1＜180°范围内使用，但事实上，当β1＞180°时，可认为目标是沿着图1所示轨迹的反方向运动，因此，仅需对算术符号做相应的改变，即可使所导出的公式适用于整个平面范围.

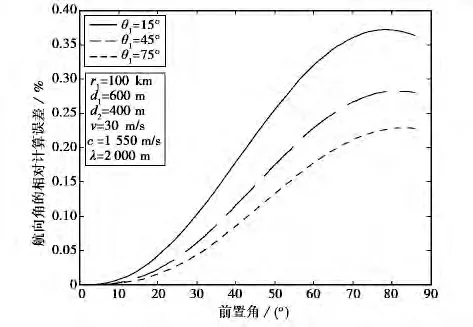
图2 航向角的真值与计算值之间的相对误差比对

在前置角90°＜β1＜180°时的计算公式为

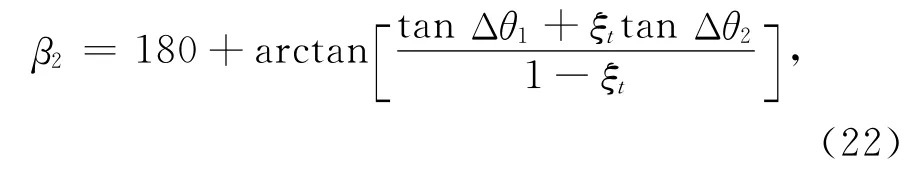
此时，航向角的计算式为

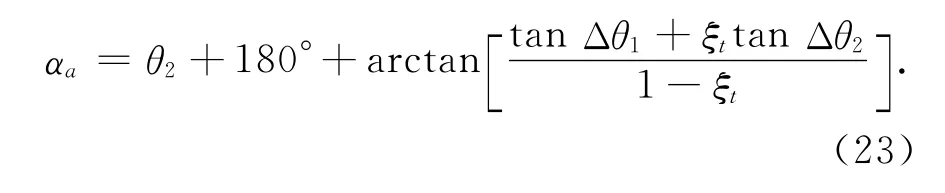
模拟计算还表明，改变相邻飞行距离的比值对计算误差所造成的影响很小.这事实上也说明，在小角度时，由正弦函数与正切函数之间的近似相等所产生的误差是极其微小的.

4 一次迭代解

数学计算表明，如利用各个运动参量的纯理论值，则从自时差方程组即可得到极其准确的结果，但事实上，由相邻观测时差ΔTi之比所给出的相邻移动距离di的比值ξd是在忽略程差项的近似简化条件下获得的，且模拟演算表明，尽管在此种近似下所获得的航向角是足够准确的，但如将此近似获得的移动距离比值代入自时差方程后去求解其它未知参量，则会出现得不到准确解的现象，微小的数值变化即可使方程的计算准确性变劣.

为此，作为一种迭代算法，在求得前置角之后，通过求解移动距离和径向距离之间的比值，以及径向距离之间的比值，再按几何定义进行计算，从而得到了准确性更好的相邻移动距离的比值.

利用式（10）和（11）解出仅和测算值β2相关的移动距离与径向距离的比值计算式：

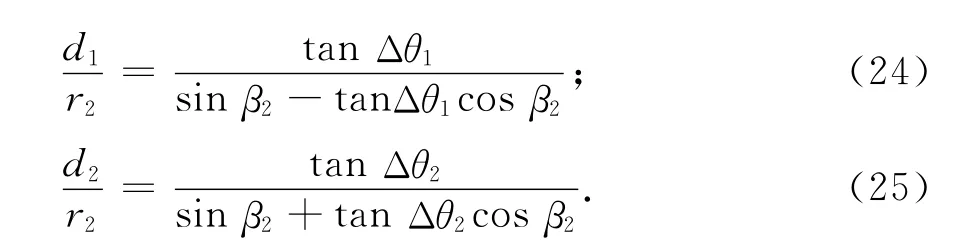
由余弦定理可得到仅和测算值β2相关的径向距离间的比值：

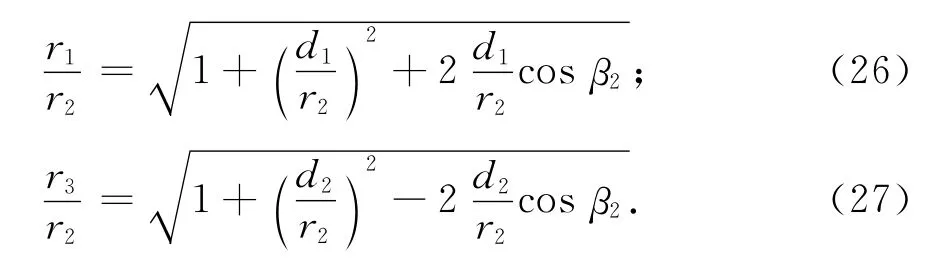
又由目标的移动轨迹和径向距离所围成的几何三角形可分别得到：

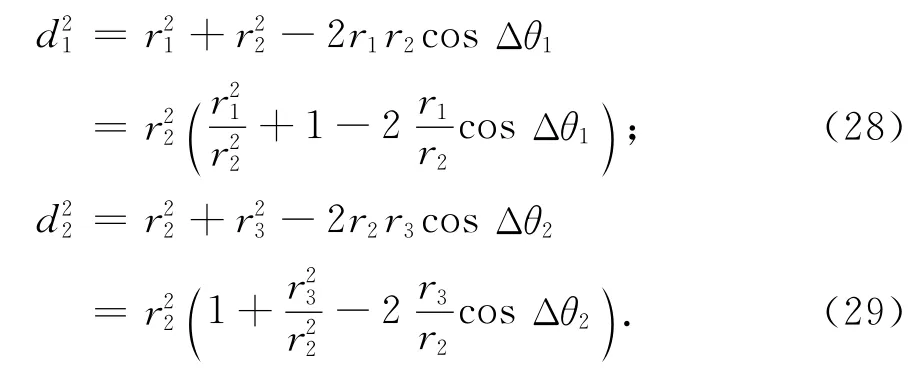
由此重新得到一个关于目标移动距离的比值

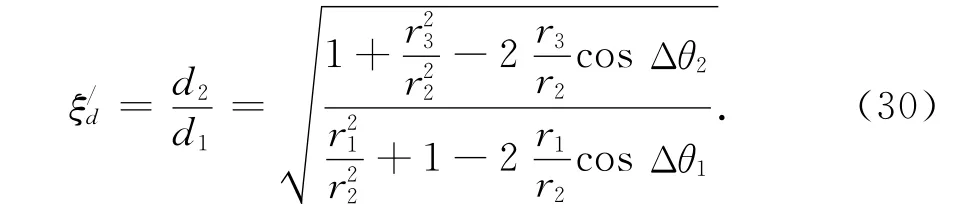
式中，相邻径向距离的比值可由式（26）和（27）确定.注意此时仍将有

但

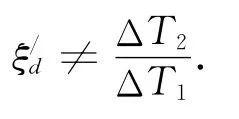
将相邻移动距离的比值关系式（30）代回式（9），即可解出准确性更好的目标前置角为：

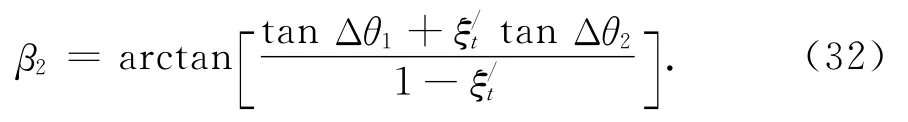
5 目标的运动参数

5.1 目标的移动速度

在自时差方程中，先将目标的移动时差用移动距离与速度的比值取代，则由两个自时差方程之比得

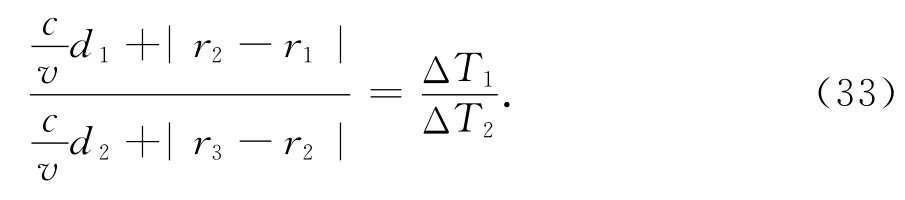
再将径向距离r2提取出来，经整理后有

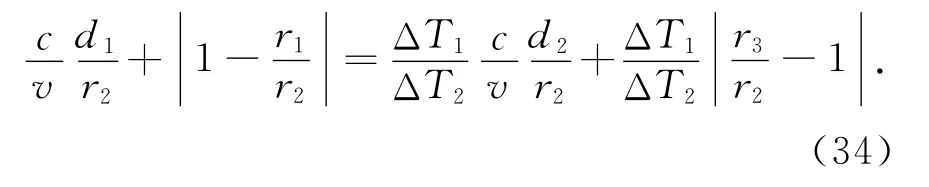
由此可解出目标的移动速度

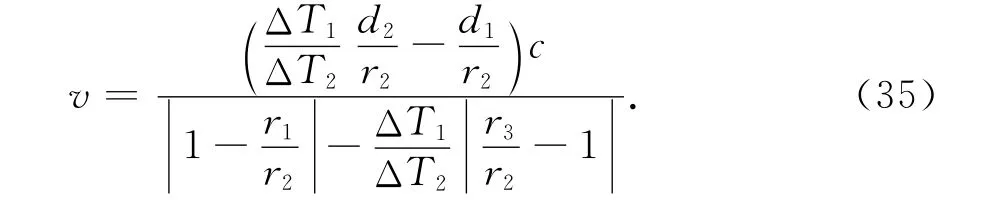
式中，移动距离和径向距离的比值采用式（24）和（25），而相邻径向距离的比值则直接按正弦定理有

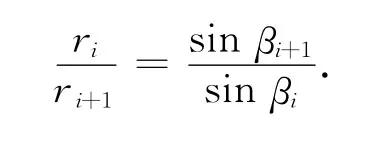
由此得

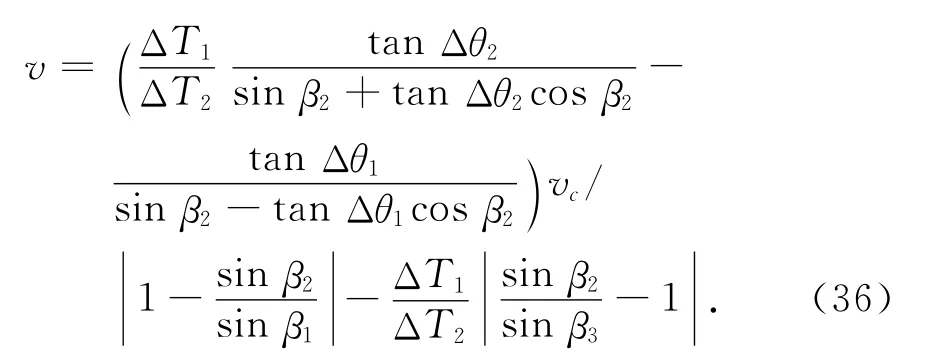
式中：Δθi通过方位的检测得到；β1和β3由迭代测算值β2计算得到，且有β1＝β2-Δθ1，β3＝β2＋Δθ2.

图3给出了不等移动距离时，目标移动速度的相对计算误差，θ1是观测站的起始测向角.

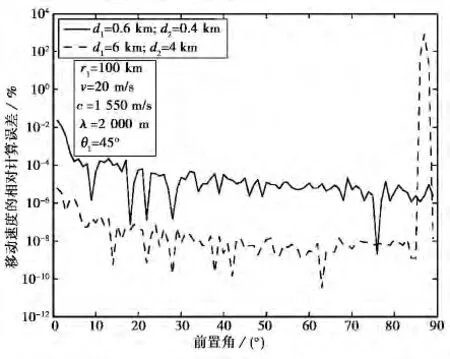
图3 目标移动速度的相对计算误差

5.2 目标的移动时差

利用径向距离间的比值关系，由自时差方程可得到如下的二元一次方程：

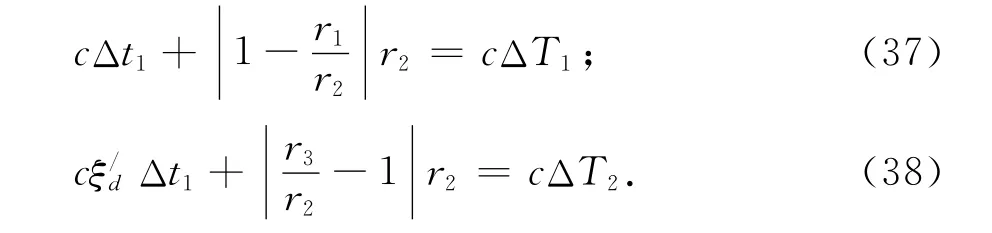
在消去径向距离r2之后，可解得目标的移动时间，其相对计算误差如图4所示.

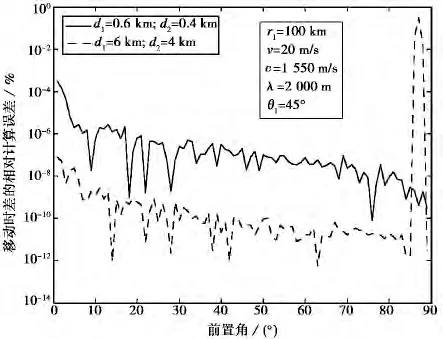
图4 目标移动时差的相对计算误差

5.3 目标的距离

事实上，在解得目标的速度和移动时间差之后，直接利用正弦定理即可求得目标的径向距离，即有

另由自时差方程，从式（34）可求解得到径向距离

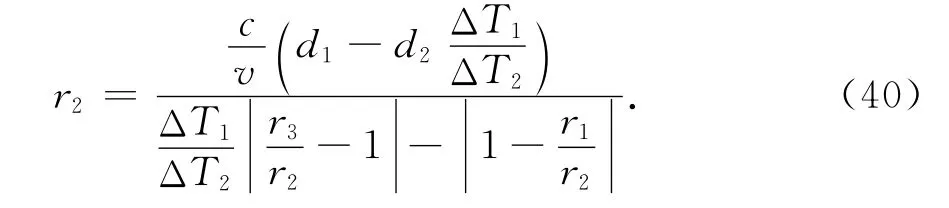
图5给出了径向距离r2的相对计算误差.

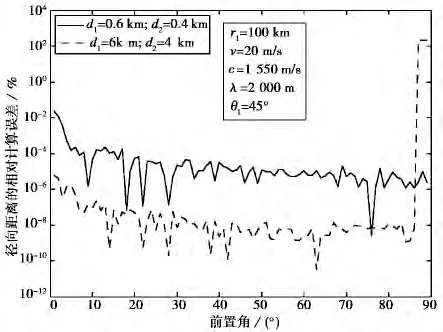
图5 径向距离的相对计算误差

由上述的模拟计算结果可知，在假定目标为匀速直线运动的情况下，按二维平面几何关系和自时差方程所得到线性方程对目标的移动速度、移动时间以及距离的计算都是相当准确的.

6 结 论

由于仅考虑了距离与速度之间的关系，故原有的纯方位目标运动分析的研究历史似乎是十分复杂而又艰难的.已有的研究表明，利用距离-速度关系条件，需在推导过程中限定相邻的移动时间差或移动距离差相等，则目标与观测站之间的距离才能够被解析求解［7］，但这种附加条件极大地限制了工程可应用性.

与仅基于距离与速度之间关系的传统分析方法相比，本文通过引入自时差测量方程，并充分利用简单的平面几何关系，能对相邻移动距离不等的一般情况，完整地给出了固定单站纯方位无源定位的解析计算公式，且通过一次迭代计算，即能消除计算过程中所存有的病态特性，获得准确的计算结果.所提出的新方法突破了现有的固定单站纯方位无源探测仅能获得目标航向，以及速度与初始距离比值的局限性.但由于目前所建立的自时差测量方程仅是一个和目标匀速运动参量相关的线性方程，并且需要连续多次观测时差，故本文所提出的方法仅适用于分析在短时间内可近似看作是直线匀速运动的目标.

［1］刘 忠，周 丰，石章松.纯方位目标运动分析［M］.北京：国防工业出版社，2009.

［2］石章松，刘 忠.单站纯方位目标跟踪系统可观测性分析［J］.火力与指挥控制，2007，32（2）：26-29.SHI Zhangsong，LIU Zhong.The analysis of the observability on the single platform bearings-only target tracking system［J］.Fire Control ＆Command Control，2007，32（2）：26-29.（in Chinese）

［3］WANG Zhi，LUO Jian，ZHANG Xiaoping.A Novel location-penalized maximum likelihood estimator for bearing-only target localization［J］.IEEE Transactions on Signal Processing，2012，60（12）：6166-6181.

［4］GAVISH M，WEISS A J.Performance analysis of bearing-only target location algorithms［J］.IEEE Transactions on Aerospace and Electronic Systems，1992，28（3）：817-828.

［5］李长文，赵海彬.有限声速的纯方位算法［J］.指挥控制与仿真，2013，35（2）：38-42.LI Changwen，ZHAO Haibin.Bearing-only arithmetic with finite sound velocity［J］.Command Control＆Simulation，2013，35（2）：38-42.（in Chinese）

［6］武志东，朱伟良，李祥珂.潜艇不机动纯方位解算编队目标运动要素方法［J］.指挥控制与仿真，2013，35（2）：43-46.WU Zhidong，ZHU Weiliang，LI Xiangke.Method for bearing only TMA without maneuvering for submarine［J］.Command Control ＆Simulation，2013，35（2）：43-46.（in Chinese）

［7］孙仲康，郭福成，冯道旺.单站无源定位跟踪技术［M］.北京：国防工业出版社，2008.