碟片式离心机内流动的数值模拟

袁惠新，侯新瑞，付双成

（常州大学分离工程研究所，江苏 常州 213016）

碟式离心机是应用比较广泛的分离机械，通过其转鼓内的多层碟片的高速旋转带动碟片间的非均相混合物产生旋转运动。利用“离心沉降”和“浅池沉降”原理不但具有较高的分离因数，可以高效地分离微细颗粒，而且由于沉降面积大，其生产能力大[1-3]。碟片式离心机按分离方式可分为澄清式和分离式，两者的区别是分离式离心机碟片开孔，液体从小孔进入蝶片间隙。本文将研究分离式碟片式离心机的内部流场，此外，碟式离心分离可实现连续操作，可用于净化、澄清和浓缩等分离过程，因而被广泛用于石油、化工、医药、轻工、船舶、食品等行业[4-5]。

由于碟片式离心机内的流场难以直接测量，人们对其内部流动的认识往往停留在经验或想象上，有些想象甚至是错误的，因此，难以对其进行客观的分析和优化。近年来，随着计算流体力学（CFD）技术的迅速发展，为流体机械的研究提供了重要研究途径[6-8]。赵志国等[9]采用 CFD技术对碟片式离心机内部流场进行二维数值模拟，并对液相油滴的轨迹进行了追踪，得出油水分离形成稳定的分层界面。针对润滑油碟片式分离机，赵志国等[10]采用VOF多相流模型并结合RNG k-ε湍流模型和离散相模型对其内部油水固分离过程和分离效率进行了数值模拟。但迄今为止，对碟片式离心机的内部流场的研究报道较少，碟片式离心机分离理论大部分基于单层碟片空间的研究，而多层碟片间的流量分配还没有研究报道，且其对设计影响非常大。所见报道模拟也多为简化的二维流场，不能很好地反映其空间流场特征。因此，本文将基于CFD技术，采用Fluent软件对DRS 2304-00-99型碟片式离心机内部流场进行三维数值模拟。

1 物理模型、网格划分及计算方法

1.1 物理模型和网格划分

表1 碟片基本尺寸

计算采用的碟片式离心机物理模型的碟片结构如图1所示，尺寸见表1。以11层碟片的空间为模型（共11层碟片，从下往上方向10个碟片间隙分别定义为第1～10层），利用Gambit软件创建几何模型并划分网格。为保证网格的质量及计算精度，采用六面体结构化网格划分和局部加密技术，网格数为1014880个，网格划分如图2所示。

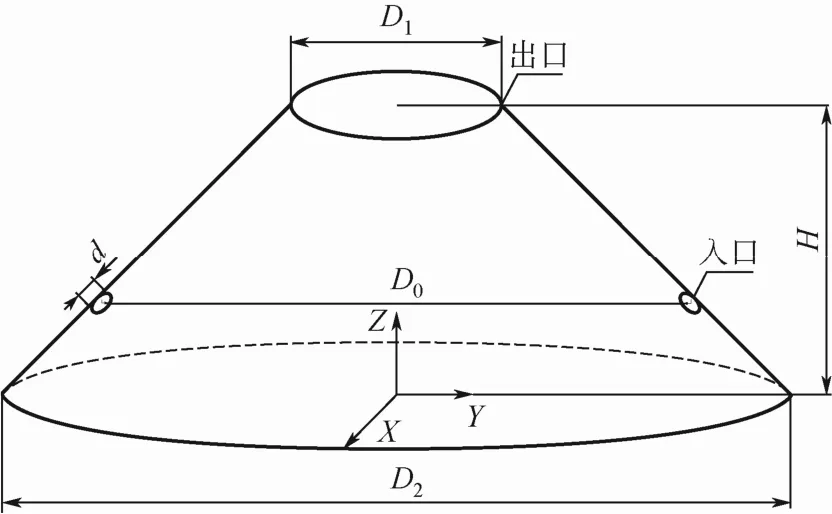
图1 碟片结构图

图2 11层碟片六面体结构化网格

1.2 控制方程和湍流模型

本文采用标准k-ε模型和多重参考系（MRF）模型，标准k-ε模型自从被Launder及Spalding提出后，就成为工程流场计算中的主要工具。它是个半经验公式，是从实验现象中总结出来的，所以有适用范围广、经济、精度合理的特点。标准k-ε 双方程模型假定湍动黏度是各向同性的，其湍动能 k和耗散率ε方程为如式（1）、式（2）所示[11]。

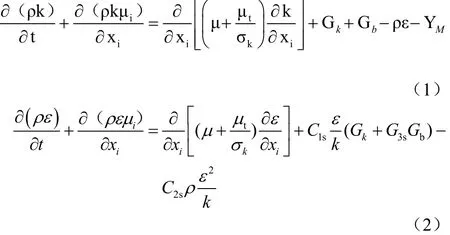
在 Fluent中，作为默认值常数，C1ε=1.44， C2ε=1.92，Cμ=0.09湍动能k与耗散率ε的湍流普朗特数分别为σk=1.0，σε=1.3。

1.3 边界条件设定及计算方法

计算采用速度进口边界条件和压力出口边界条件。入口速度为0.32m/s（即处理量为0.72m3/h），入口湍流强度为5%，出口压力为表压0Pa。在多重参考系中，设置碟片转速为1000r/min，方向为顺时针方向（沿着 Z轴向正方向看）。壁面采用标准壁面方程处理，离散控制方程时，对压力项采用二阶中心差分格式，对动量方程、湍动能、湍耗散方程采用二阶迎风差分格式，压力修正法采用压力耦合方程组的半隐式方法（SIMPLE算法）。

2 数值模拟结果与分析

2.1 速度分布

2.1.1 周向速度

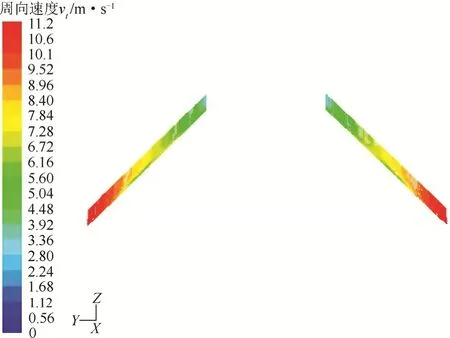
图3 纵截面处的周向速度分布云图

周向速度反映了流体在碟片式离心机内旋转的快慢，决定了离心力的大小。由图3周向速度分布可以看出，单层碟片间隙内的周向速度由内至外逐渐增大，从而由上至下逐渐增大。从多层碟片来看，周向速度由内至外逐渐增大，符合vt=ωr的基本规律。在Z=10mm截面处取X=0上的一条直线定义为line10，周向速度的模拟曲线与理论曲线的比较如图4所示。理论曲线根据经典的理论公式vt=ωr计算。由图4可以看出，几乎在所有径向位置，周向速度模拟小于理论值。像螺旋卸料离心机一样，流体的转动滞后于碟片。其中，第3～5层旋转滞后较为明显。但由于碟片间隙较小，所以滞后较小。由此可以得出，碟片间隙小不仅可以减小沉降距离，还可以减小流体旋转的滞后，这有利于提高颗粒的分离效率[12]。实际应用中，每层碟片上沿碟片母线都有筋条（本文为简化模型，已省去），流体的转动滞后可以更小。

图4 直线line10周向速度分布

2.1.2 轴向速度

轴向速度是影响离心机处理量的一个物理量，流速越大，则离心机处理量越大。但是轴向速度大，物料在碟片间的停留时间短，不利于颗粒的分离。另外，轴向速度太大会扰动已经沉降的沉渣，导致分离效果下降。图5所示为X=0截面轴向速度云图。从图5可以直观地看出，内层碟片间隙内的轴向速度较大。第1～10层碟片间隙内同一半径不同轴向位置的轴向速度如图6所示。从总体趋势来看，由于料液进入每一组碟片的流量不均匀，第1～10层碟片间隙内轴向速度大小呈递减趋势，到第5层之后速度变化减缓。从单个碟片间隙来看，第 1～2层碟片间隙内，轴向速度不同于周向速度，流体靠近碟片壁面的轴向速度小，中间位置速度大。第3～10层呈现 M 形驼峰分布，符合普朗特边界层理论[13]。由此可以得出，由于前两层轴向速度vZ较大，周向速度vt相近，这就导致了前两层碟片间隙内的流量相差大，说明碟片间的流量分布不均匀。

图5 X=0截面轴向速度分布云图

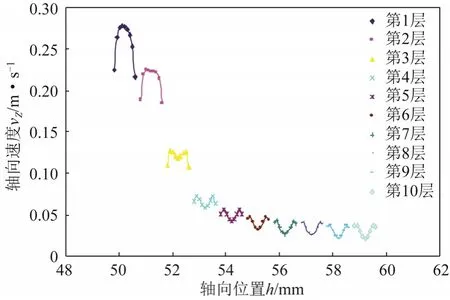
图6 不同层的轴向速度分布

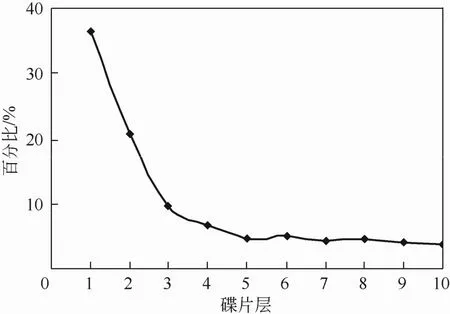
图7 各层碟片间出口流量占处理量的百分比

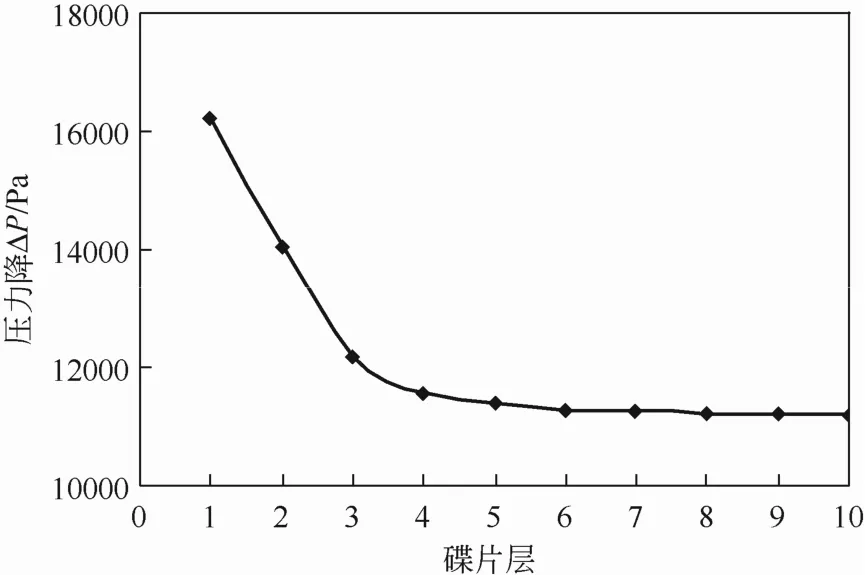
图8 不同层碟片间压力降

2.2 不同层碟片间的流量分配

每层碟片间出口流量占总处理量的百分比如图7所示，每层碟片间出口流量值占处理量的百分比从第1～10层呈下降趋势，第1～3层急剧下降，到第5层后下降趋势减缓，其中前3层的出口流量所占比例较大。不同层碟片间的压力降如图8所示，从第1～10层碟片间隙内（从下往上）压力降越来越小，进一步说明了出口流量呈减小趋势的原因。从第1～10层碟片间隙内，由于压力降的减小，料液向上运动的推动力随着减小，使轴向速度减小，间接导致流量的减小。从结构上分析，由于入口小孔流通面积较小，阻力较大，导致前几层碟片内液体流量较大，而越往上液体流量越小。由此得出，对于多层碟片式离心机来说，每层碟片间隙内的流量是不均等的，且前几层碟片间隙内的流量较大。

2.3 压力分布

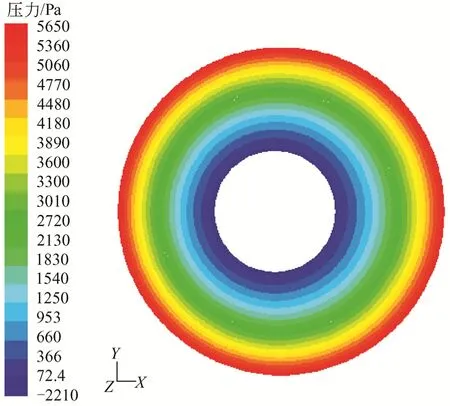
图9 第11层碟片壁面压力分布云图

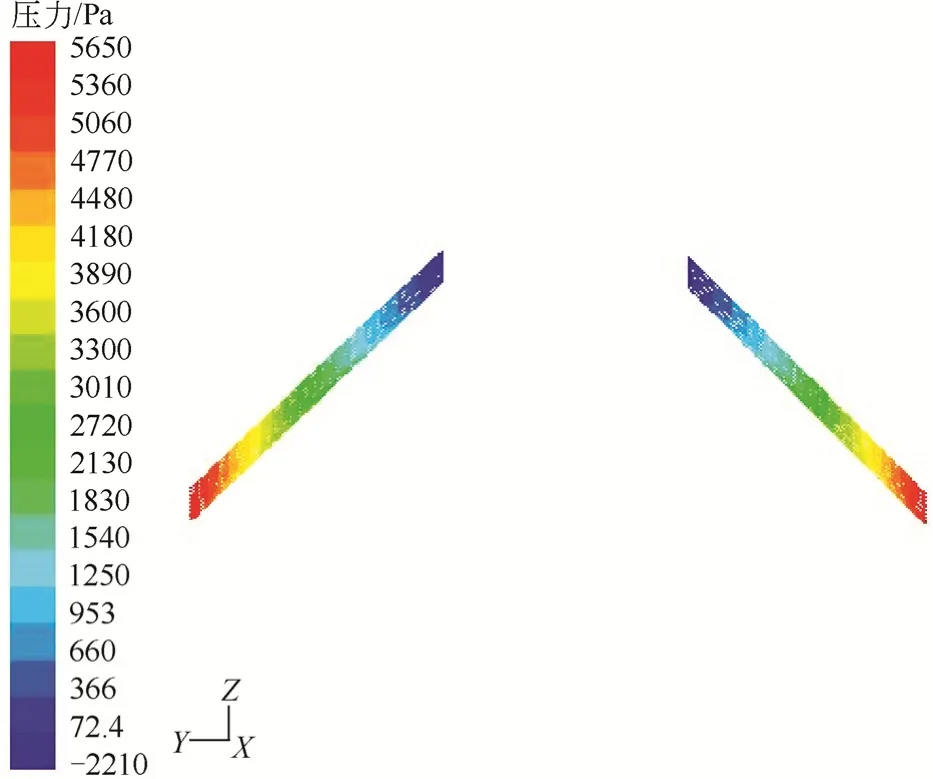
图10 X=0mm截面压力分布云图

3 结 论

通过对多层碟片的碟片式离心机内三维流场的数值模拟研究，对碟片式离心机内的流动有了更加全面的认识，得出如下主要结论。

（1）通过三维数值模拟可直观地看出，速度分布云图和压力分布云图符合碟片式离心机的内部理论基本规律，说明用Fluent软件模拟碟片式离心机内部流场流动状况的方法是可行的。

（2）通过模拟发现，碟片在高速旋转时，碟片间的流体存在旋转滞后现象。减小碟片间隙不仅可以减小沉降距离，还可以减小流体旋转滞后，这将有利于提高颗粒的分离效率。

（3）每层碟片间的出口流量是不均等的，从第1～10层流量呈减小趋势。其中前3层碟片间的流量约占66%。

[1] 孙启才，金鼎五.离心机原理结构与设计计算[M].北京：机械工业出版社，1987.

[2] 袁惠新，冯骉.分离工程[M].北京：中国石化出版社，2002：108-139.

[3] 戴金河，褚强.高岭土精制浓缩工艺及设备[J].中国非金属矿工业导刊，2012（4）：45-47.

[4] Rushton A，Word A S，Holdich R G.固液两相过滤及分离技术[M].朱企新等译.北京：化学工业出版社，2005.

[5] 刘广明.碟式分离机分离效果的分析研究[J].过滤与分离，2009，19（1）：27-30.

[6] 翟建华.计算流体力学（CFD）的通用软件[J].河北科技大学学报，2005，26（2）：160-165.

[7] He P，Salcudean M.A numeirical simulation of hydrocyclones[J].Transation of the Institution of Chemical Engineers，1999，77（A）：429-439.

[8] 姚征，陈康民.CFD通用软件综述[J].上海理工大学学报，2002，24（2）：137-144.

[9] Zhao Zhiguo.The influence of structural changes on the interior flow field’s characteristics of dics separator [J].Procedia Engineering，2011，15：5051-5055.

[10] 赵志国，石博强，李宴，等.润滑油分离机内部流场数值模拟与分离效率分析[J].农业工程学报，2011，27（8）：163-168.

[11] 吴玉林，曹树良，葛亮，等.渣浆泵叶轮中固液两相湍流的计算和实验[J].清华大学学报：自然科学版，1998（1）：71-74.

[12] Wang Yanm in，Forssberg Eric，Li Jingxian，et al.Continuous ultra-fine classification in a disc-stack nozzle centrifuge-effects of G-forces and disc geometry[J].China Particuology，2003，1（2）：70-75.

[13] 林建忠，阮晓东，陈邦国，等.流体力学[M].北京：清华大学出版社，2005.