基于轨迹灵敏度和FASTICA 的同调机群识别方法

王永贵，卫志农，孙国强，何 桦

（1.河海大学可再生能源发电技术教育部工程研究中心，南京210098；2.南瑞继保电气有限公司，南京211100）

电力系统各发电机组在动态过程中存在着同调现象，即不同发电机机组动态特性的一致性或相似性。追求准确、快速地识别同调机群对于研究电力系统稳定性具有重要意义。目前，同调机群的识别方法很多，如自组织神经网络法[1]、特相关系数法[2]、改进模糊ISODATA 法[3]、改进的免疫算法[4]、模糊聚类法[5]、主成分分析[6]等。这些方法各有侧重点，如自组织神经网络法侧重于接近时域仿真结果；改进模糊ISODATA 法侧重于减少计算量，提高计算速度；而主成分分析侧重于提高分析效率。

从提高分群准确性的角度出发，把近似摇摆曲线轨迹灵敏度及FASTICA 技术用于电力系统同调机群的识别。直接对机组近似摇摆曲线轨迹灵敏度数据进行FASTICA 和聚类分析，通过特征提取判断出各机群的同调性。这种方法的物理意义清晰，依据发电机功角变化的趋势进行机组分群，比传统单凭发电机功角差[7]的方法更能体现发电机动态行为间存在的相似性，可有效提高分群的准确性。以IEEE 39 节点和IEEE 145 节点2 个试验系统作为算例，验证本方法的有效性。

1 发电机近似摇摆曲线轨迹灵敏度分析

轨迹灵敏度法[8～10]在电力系统动态安全分析中有着广泛的应用，它可以计算沿系统运行轨迹的灵敏度以及参数对动态响应的灵敏度，通过轨迹灵敏度可求得发电机功角动态变化的趋势。

为了快速准确地判别发电机同调机组，对系统元件作必要简化，并作以下基本假定[7]。

（1）同调组的划分应与扰动大小无关，从而可把系统线性化，化为增量形式的方程组表示，用其动态行为判别同调。

（2）发电单元的细节描述对同调组的划分影响较小，故同调判别时发电机可用经典二阶模型来描写，忽略励磁系统和原动机、调速器的动态。

（3）同调组的划分与负荷模型关系较小，则同调判别时负荷化为等值阻抗描述，并入导纳阵。

在上述假定基础上，系统可以大大地简化，有利于快速作同调机组判别，并仍能满足准确判别同调机组的要求。

系统线性化转子动态方程为

式中：x为状态变量，x=（Δω，Δδ）T；δ 为发电机转子角，rad；ω 为发电机转子角速度，rad/s；y 为系统的运行参量。应用龙格-库塔方法，对式（1）进行迭代求解，得

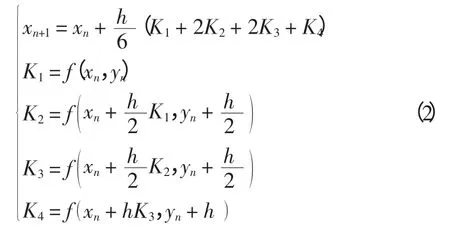
式中，h 为积分步长。

计算出发电机摇摆曲线，即可求得Δδi（t）。发电机近似摇摆曲线的轨迹灵敏度zi（t）为

2 快速独立分量分析算法

FASTICA 算法是芬兰赫尔辛基工业大学Hyvärinen 等[11]提出并发展起来的，该算法基于非高斯性最大化原理，使用固定点迭代理论寻找WTx的非高斯性最大值，采用牛顿迭代算法对观测变量x的大量采样点进行批处理，每次从观测信号中分离出一个独立分量。这是独立分量分析ICA（independent component analysis）[12～13]的一种快速算法，其非高斯性度量函数为

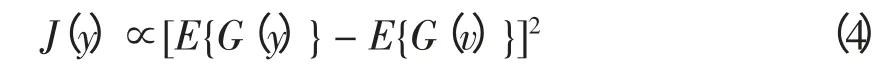
其中：E（·）为均值运算；G 为任意非二次型函数。

为了减少算法需要估计的参数，简化计算，在运行FASTICA 算法之前，需要对数据进行预处理。

在非高斯性最大化方法中，FASTICA 算法利用基于式（4）的负熵表达式来估计独立分量。首先为了找出第i 个独立分量，或求出yi=wTx 的投影方向，使式（4）的值最大化[14]，即

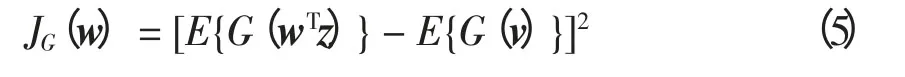
式中：w 为m 维变量；v 为与y 具有相同均值和协方差矩阵的高斯变量。

预处理后（v 为零均值、单位方差的高斯变量时，可以忽略不计），式（5）的最大化问题可以转化为E{G（wTx）}的优化问题。按照Kuhn-Tucker 条件，E{G（wTx）}的优化约束条件为

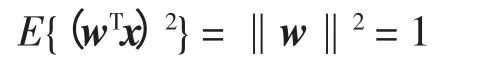
约束条件通过白化处理获得，即

用牛顿迭代法解式（6）。式（6）函数等式左边部分记为F（w），其雅可比矩阵JF（w）为

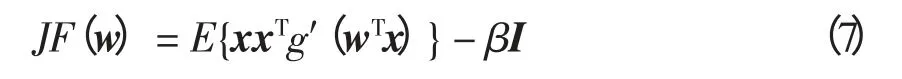
为了简化矩阵求逆，对E{xxTg′（wTx）}进行近似。因为数据已经预处理，可近似为

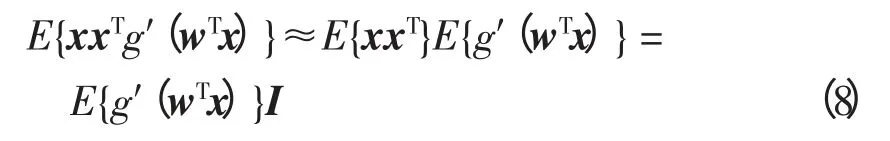
雅可比矩阵是非奇异矩阵、对角矩阵，可以很容易对其求逆。同样地，对常量β 用当前w 的值替代w0的值，可以得到式（8）的牛顿迭代法的近似解为

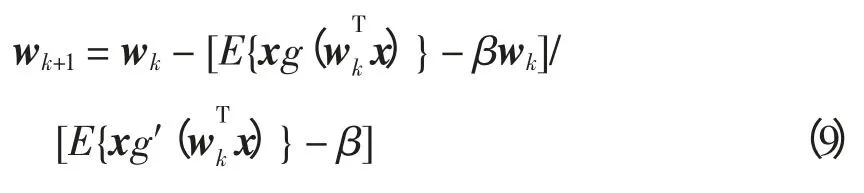
其中，β=E{wTxg（wTx）}。为了提高算法的稳定性，迭代后令

归一化w。在式（9）两边乘以β-E{g′（wTx）}，得到固定点算法的迭代公式，即

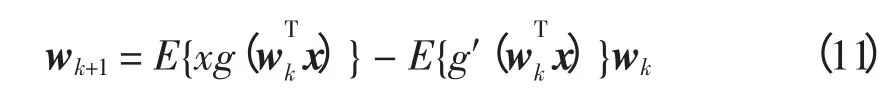
求出wk，k=1，2，…，n，即可构成分离矩阵W。

3 对轨迹灵敏度的特征提取和聚类

首先对近似摇摆曲线的轨迹灵敏度z 进行预处理。预处理包括去均值和白化两个部分[14]。

去均值是FASTICA 算法最基本的预处理步骤，其处理过程是从z 中减去z 的均值向量m =E{z}，使得z 成为零均值变量。该预处理只是为了简化FASTICA 算法，并不意味着均值不能估计出来。用去均值的数据估计分离矩阵W 后，可以在源信号的估计值y 上加上均值。

去均值后，对z 进行白化处理，使得白化后的分量z~为非相关的，且为单位方差，即满足

常用的白化算法为

式中：D-1/2为n × n 阶对角特征值矩阵，D-1/2=；E 为m×n 阶特征向量矩阵，E=[c1，c2，…，ci，…，cn]；di为观测信号的协方差矩阵E{zzT}的第i 个特征值；ci为di对应的特征向量。

通过去均值和白化得到z~，对z~作FASTICA，得

通过求逆或伪逆得

式中，[W]#为W 的逆或伪逆。

分离矩阵W 即为通过FASTICA 得到的特征提取器，利用它将高维数据降维变换到低维空间，进行投影寻踪和模式识别。矩阵[W]#的各行元素反映了每台发电机在受扰后的摇摆曲线轨迹灵敏度变化特征，对各行元素进行聚类分析，并结合2 维或3 维空间观察结果，就能快速、清晰地了解发电机的同调情况。

k 均值聚类[15]是一种常用的聚类算法，其基本思想是首先确定几个初始聚类中心，然后逐步改变或调整这些中心，使聚类趋于合理。该算法简单高效。对包含m 行向量的特征矩阵[W]#，将其分为k 个同调群C1，C2，…，Ck，Ni为第i 个群Ci中的发电机数目，ei为这些发电机的特征均值，距离函数d 为欧氏距离，分群结果求取步骤如下。

步骤1 随机选择k 个样本作为初始聚类中心c1，c2，…，ck。

步骤2 若d（m1，ep）≤d（mj，ei）；1≤p≤k；i =1，2，…，k，则分配mj到第p 类。

步骤3 重新计算每个聚类的中心

步骤4 重复步骤2 和步骤3，直到ei不再变化，即将系统中的机组分成了k 个同调群。

4 算例仿真

为了验证本算法的有效性和可行性，对IEEE 39 节点系统、IEEE 145 节点系统和某省级电网进行了仿真计算。

4.1 IEEE 39 节点系统

IEEE 39 节点系统接线如图1 所示。在线路bus2 侧设置三相短路故障，5 个周波后故障消除，除平衡机（母线编号为31 的发电机）不进行同调聚合外，其他9 台发电机与母线编号的对应关系如表1 所示。

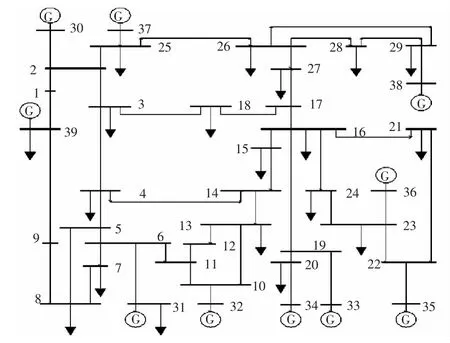
图1 IEEE39 节点系统Fig.1 IEEE 39-bus system

表1 IEEE 39 节点系统发电机编号与母线编号的对应关系Tab.1 Corresponding relationships between system generator numbers and bus numbers

求解式（3），得到近似摇摆曲线的轨迹灵敏度。对轨迹灵敏度数据进行FASTICA，预处理过程中的主元分析结果表明协方差阵E{zzT}中取2 个主值时，特征根方差贡献率已达很高的比例。故只需从测量数据中提取二维独立分量即可满足计算精度。进一步分析得到的各机组相应的特征矩阵[W]#1如表2 所示。

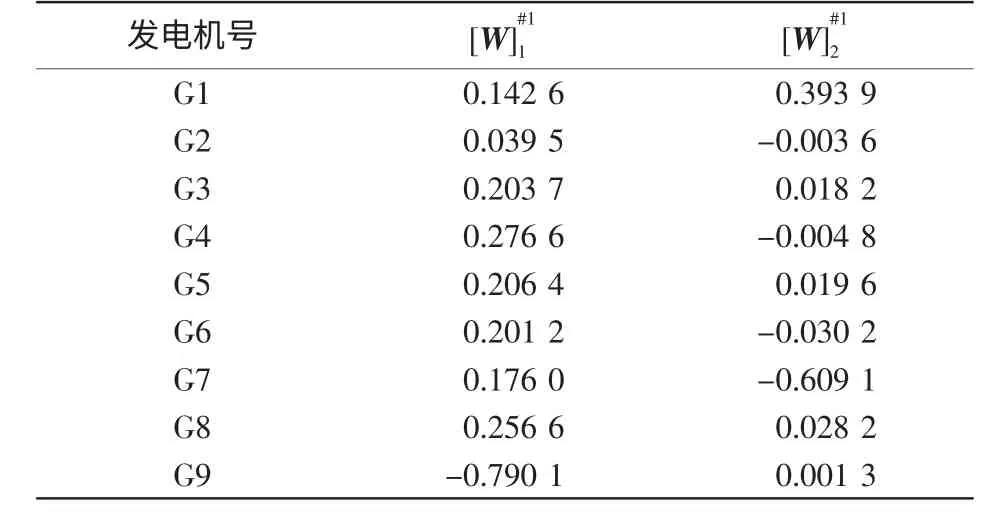
表2 轨迹灵敏度法中矩阵[W]#1 的元素Tab.2 Elements of matrix[W]#1 in the method of trajectory sensitivity

将特征矩阵[W]#1中的元素投影到一个二维平面上，可清楚地观察到受扰后各机组的同调情况，如图2 所示。

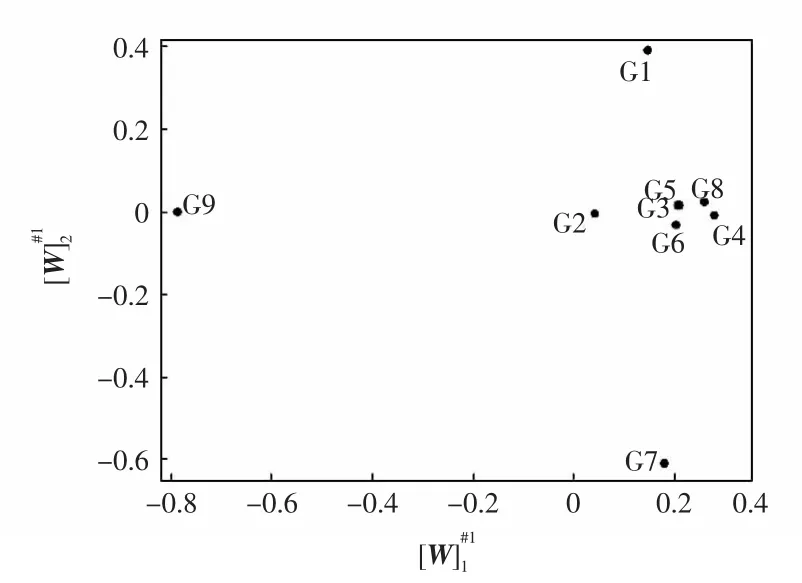
图2 IEEE39 节点系统轨迹灵敏度法的同调特性Fig.2 Identification of the IEEE 39-bus system coherent generators by the method of trajectory sensitivity

由图2 可知，若将机组分为6 群，分群结果为：①｛G1｝；②｛G2｝；③｛G3，G5，G6｝；④｛G7｝；⑤｛G4，G8｝；⑥｛G9｝。若使用k 均值聚类，给定k=6，可以得到相同的结果。

同理，在相同故障下，采用依据功角差为标准的传统分群方法，运用FASTICA 得到各机组相应的特征矩阵[W]#2，如表3 所示。

将特征矩阵[W]#2中的元素投影到一个二维平面上，如图3 所示。

同样，若将机组分为6 群，分群结果为：①｛G1｝；②｛G2｝；③｛G3，G5，G6｝；④｛G7｝；⑤｛G4，G8｝；⑥｛G9｝。与k 均值聚类得到的结果相同。

两种方法分群结果相同，但从k 均值聚类过程中得到的类间所有点与该类质心点距离之和，可以发现运用轨迹灵敏度法中的同一群机组分布情况与传统方法有着较大差异，如表4 所示。

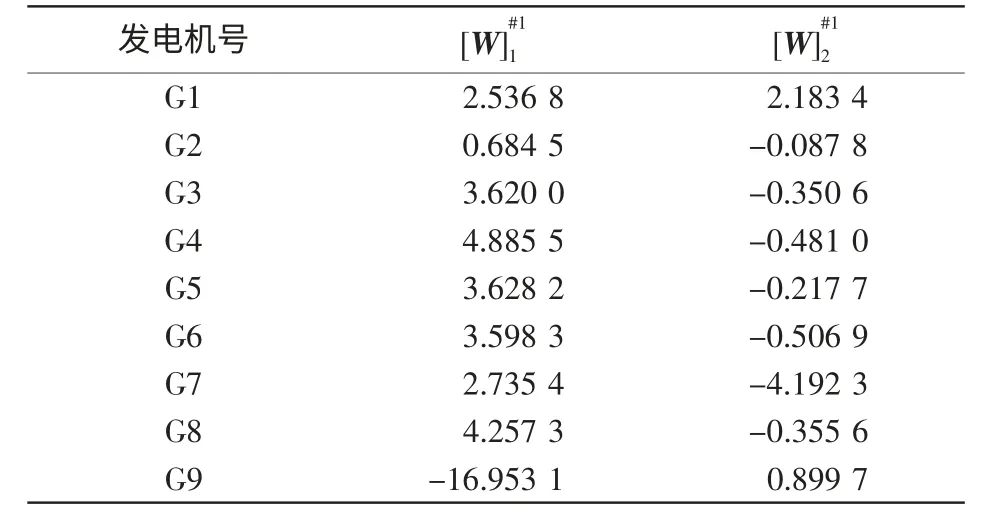
表3 传统方法中矩阵的元素Tab.3 Elements of matrix in the traditional method

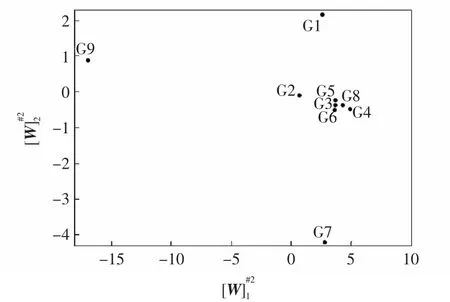
图3 IEEE 39 节点系统传统方法的同调特性Fig.3 Identification of the IEEE 39-bus system coherent generators by the traditional method

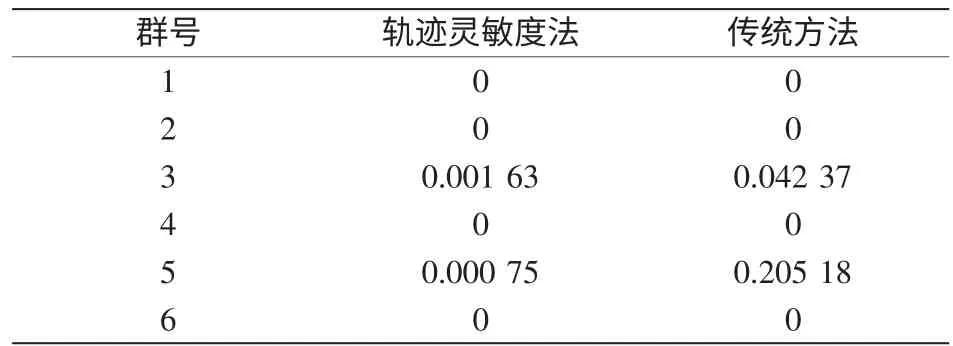
表4 IEEE 39 类间所有点与该类质心点距离之和Tab.4 Sum of the distance of all points to the center of the type in IEEE 39

由表4 可知，运用轨迹灵敏度分群类间所有点与该类质心点距离之和比用传统方法小得多，每类中各发电机分布更为集中，分群更为精确。即发电机功角变化的趋势进行机组分群，比传统单凭发电机功角差的方法，更能体现发电机动态行为间存在的相似性。

4.2 IEEE 145 节点系统

IEEE 145 节点系统接线如图4 所示。在线路bus7 侧设置三相短路故障，5 个周波后故障消除。类间所有点与该类质心点距离之和如表5 所示。

由表5 可知，同一群机组分布仍然比较集中。随着网络规模的增大，该算法的有效性和准确性均是有保障的，并且迭代次数没有明显的影响。从测试结果可知，程序的运行效率可满足计算的要求。

图4 IEEE 145 节点系统Fig.4 IEEE 145-bus system

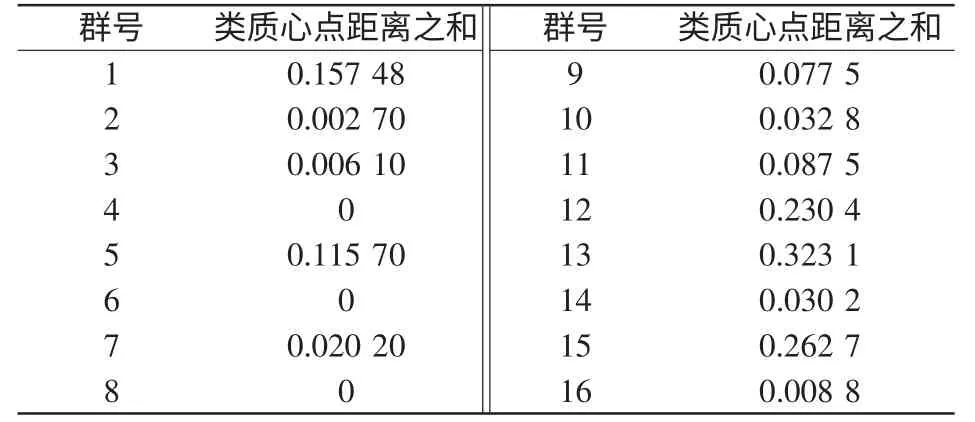
表5 IEEE 145 类间所有点与该类质心点距离之和Tab.5 Sum of the distance of all points to the center of the type in IEEE 145

4.3 某省级电网

为验证本方法对实际系统的有效性和可行性，本文还对某省级电网进行仿真计算。设置相同故障，随机选取电网中的10 台机组，运用两种方法进行分群，分群结果和类间所有点与该类质心点距离之和分别如表6、表7 所示。

由表6 可知，在实际系统中，本文方法较传统方法的分群结果相似。然而表7 的结果表明，本文方法每类中各发电机分布更为集中，分群更为精确，同时也说明了本文方法能运用于大系统分析。

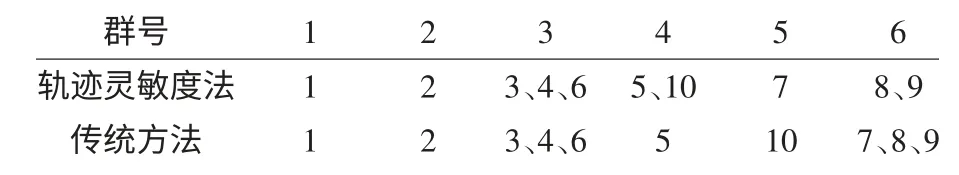
表6 2 种方法分群结果Tab.6 Clustering results of two methods

表7 某省级电网类间所有点与该类质心点距离之和Tab.7 Sum of the distance of all points to the center of the type in a power grid

5 结论

本文基于发电机近似摇摆曲线轨迹灵敏度和FASTICA 提出了一种发电机同调机群识别方法。在发电机近似摇摆曲线轨迹灵敏度基础上，运用FASTICA 方法，快速地识别出发电机同调机群。通过不同算例的测试结果验证了本文算法的有效性和可行性。本文的模型和方法具有2 大特点。

（1）从发电机近似摇摆曲线轨迹灵敏度出发，依据发电机功角变化的趋势进行机组分群，比传统单凭发电机功角差的方法更能体现发电机动态行为间存在的相似性，可有效提高分群的准确性。

（2）运用FASTICA 方法，将高维轨迹灵敏度数据降维变换到低维空间进行投影追踪和模式识别，能够准确快速地识别出发电机同调机群。

[1]刘绚，文俊，刘天琪（Liu Xuan，Wen Jun，Liu Tianqi）.基于自组织神经网络的模糊聚类同调机群识别（A fuzzy clustering method to recognize coherent generator groups based on self-organizing neural network）[J]. 电网技术（Power System Technology），2010，34（7）：98-102.

[2]Kim H，Jang G，Song K. Dynamic reduction of the largescale power systems using relation factor [J]. IEEE Trans on Power Systems，2004，19（3）：1696-1699.

[3]卫志农，王华芳，张湘艳，等（Wei Zhinong，Wang Huafang，Zhang Xiangyan，et al）.改进模糊ISODATA 法识别电力系统同调机群（Improved fuzzy ISODATA method for identification of coherent generator groups）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2006，18（6）：43-47.

[4]刘丽霞，罗敏，李晓辉，等（Liu Lixia，Luo Min，Li Xiaohui，et al）.电力系统常用动态等值方法的比较与改进（Comparison and improvement of common methods of dynamic equivalence in power system）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2011，23（1）：149-154.

[5]赵书强，常鲜戎，潘云江（Zhao Shuqiang，Chang Xianrong，Pan Yunjiang）.电力系统同调机群识别的一种模糊聚类方法（A fuzzy clustering method for coherent generator groups recongnition in power systems）[J].电网技术（Power System Technology），2001，25（4）：10-13.

[6]安军，穆钢，徐炜彬（An Jun，Mu Gang，Xu Weibin）.基于主成分分析法的电力系统同调机群识别（Recognition of power system coherent generators based on principal component analysis）[J].电网技术（Power System Technology），2009，33（3）：25-28.

[7]王建功，闫有朋，云昌钦（Wang Jiangong，Yan Youpeng，Yun Changqin）.发电机群相关识别算法假设条件的验证（Validation of assumptions in algorithms for coherent generators identification）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2005，17（4）：53-58.

[8]郑晓雨，贺仁睦，马进，等（Zheng Xiaoyu，He Renmu，Ma Jin，et al）. 基于轨迹灵敏度的负荷分类（A method of load classification based on the trajectory sensitivity）[J].电工技术学报（Transactions of China Electrotechnical Society），2010，25（9）：145-150.

[9]潮铸，刘明波（Chao Zhu，Liu Mingbo）.基于2 阶轨迹灵敏度的暂态稳定约束最优潮流计算（Transient stability constrained optimal power flow calculation based on second-order trajectory sensitivity）[J]. 电 网 技 术（Power System Technology），2011，35（7）：106-112.

[10]穆钢，王宇庭，安军，等（Mu Gang，Wang Yuting，An Jun，et al）.根据受扰轨迹识别电力系统主要振荡模式的信号能量法（Signal energy method for identification of main oscillation mode in power system based on disturbed trajectory）[J]. 中国电机工程学报（Proceedings of the CSEE），2007，27（19）：7-11.

[11]Hyvärinen A. Fast and robust fixed-point algorithms for independent component analysis[J].IEEE Trans on Neural Networks，1999，10（3）：626-634.

[12]Aapo H，Juha K，Erkki O.Independent Component Analysis[M].New York：JohnWiley&Sons，Inc，2001.

[13]孙云莲，罗卫华，李洪（Sun Yunlian，Luo Weihua，Li Hong）.基于EMD 的ICA 方法在电力载波通信信号提取中的应用（Extract signals of power line communication by a novel method based on EMD and ICA）[J].中国电机工程学报（Proceedings of the CSEE），2007，27（16）：109-113.

[14]曾生根，朱宁波，包晔，等（Zeng Shenggen，Zhu Ningbo，Bao Ye，et al）.一种改进的快速独立分量分析算法及其在图象分离中的应用（A modified fast independent component analysis and its application to image separation）[J].中国图象图形学报（Journal of Image and Graphics），2003，8（10）：1159-1165.

[15]潘炜，刘文颖，杨以涵（Pan Wei，Liu Wenying，Yang Yihan）.采用受扰轨迹和独立分量分析技术识别同调机群的方法（Method of identifying coherent generator groups by independent component analysis through perturbed trajectories）[J]. 中国电机工程学报（Proceedings of the CSEE），2008，28（25）：86-92.