基于实测数据的发电机调速系统参数辨识方法

孙 闻，孔祥玉，张 科，张 芳，杨 群

（1.广东电网公司电力科学研究院，广州510080；2.天津大学智能电网教育部重点实验室，天津300072；3.广东电网公司佛山供电局，佛山528000）

发电机调速系统的仿真模型和参数的准确程度直接关系到系统的安全稳定运行水平[1]。常规的同步发电机参数测试中，由于缺乏实际数据，仿真数据常采取“典型”模型和“保守”的参数，致使仿真结果与实际过程存在差异，难以正确反映电力系统动态安全特性，也难以为电网运行方式、电力生产提供正确指导。

调速器和原动机结合在一起的简化模型可以称为调速系统模型，IEEE 早在1968年和1981年就提出了20 余种励磁系统和调速系统模型[2]。中国电力科学研究院对于再开发的BPA、PSASP 等电力系统仿真分析程序，也给出了典型原动机及调速系统动态模型[3]。因此在当前发电机实测过程中，研究重点是模型的确认，即动态仿真的模型以及参数对实际系统的描述是否足够准确[4]，其中基于实测的发电机组参数辨识则成为参数实测工作的重要内容。

发电机调速系统的参数辨识本质上是一个优化问题，不同的优化算法形成不同的参数辨识方法。目前发电机调速系统的辨识主要分为线性和非线性辨识方法。常见的线性系统辨识方法包括基于频域响应和时域响应的经典辨识方法[5]、基于最小二乘系列的辨识算法、梯度校正法和极大似然法的现代辨识方法[6]，这些线性方法在实测工作中经常用到。线性系统辨识方法能够解决部分非线性系统参数辨识问题，但对于发电机调速系统中的强非线性参数，常规的线性系统辨识方法不再适用。由于非线性环节形状各异、模型复杂，难以写出统一表达式，目前尚缺少统一的非线性辨识理论，常见的启发式方法包括级联模型、神经网络、模糊系统与智能优化等，已初步应用于发电机调速系统参数辨识[7～8]。但此类方法存在泛化能力的问题，在工程应用中如何结合实测进行辨识，是一项有意义的研究工作。

本文结合当前电力企业广泛开展的发电机组参数实测工作，提出一种参数解耦辨识和整体辨识相结合的发电机调速系统启发式参数辨识方法。该方法对具有输入输出量测数据，能够进行参数解耦的环节，进行单独辨识；在此基础上对其他难以解耦和获得输入输出数据的环节，与已辨识参数环节组成一个整体，基于粒子群算法进行整体辨识，寻找最优拟合值，从而实现拟辨识参数的估值。

1 发电机模型及参数

发电机调速器通过控制汽轮机汽门开度或水轮机导水叶开度实现功率和频率的调节，通过改变调速器参数及给定值，能够得到所要求的发电机功率－频率调节特性[5]。以BPA 商业软件为例，目前国内主要采用的模型包括调速器和原动机组合在一起的模型（GG、GH、GC）、液压调速器模型（GS、GW）和电调型调速器模型（GA、GIGI+、GJ）等。由于发电机类型不同，其调速系统模型也有所不同，本文以广东某水电机组为例，将发电机调速系统解耦为电子调节器、执行机构和原动机3 部分，调节系统模型输出YPID 信号，执行机构模型根据YPID 信号模拟导叶开度的动作情况，以此影响原动机模型的仿真功率输出。

1）电子调节器部分

电子调节器部分的计算模型如图1 所示。图中fg为机组频率，fc为给定频率，bt为暂态转差率，Td为缓冲时间常数，Tn为加速度时间常数，T1v为微分衰减时间常数，S 为拉普拉斯算子，bp为永态转差率，ef为人工频率死区，YPID为调节程序输出，Yc为给定开度，Pc为给定功率，Pg为机组功率，K1和K2为开关（两者保持同步，K1的端子1 和2 接通，则K2的1 和2 亦接通）。

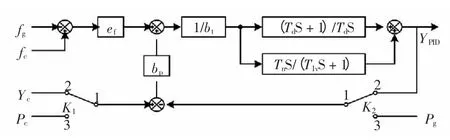
图1 电子调节器计算模型Fig.1 Model of electronic regulator

该部分需要对bt、Td、Tn、T1v等参数进行校验和辨识。参数fc设定为1，标么值；人工频率死区ef，标么值，可由人工频率死区校验获得；永态转差率bp可由永态转差系数校验获得；Yc为实测开度初始值；Pc为实测功率初始值；Pg为机组功率。

2）执行机构部分

执行机构部分的计算模型如图2 所示。图中YPID为电子调节器输出，Y 为执行机构输出（接力器行程），Um为主配压阀死区，USmax为主配压阀开启方向最大位移，LSmax为主配压阀关闭方向最大位移，Ty为接力器反应时间，Ymax为接力器最大行程，Ymin为接力器最小行程。

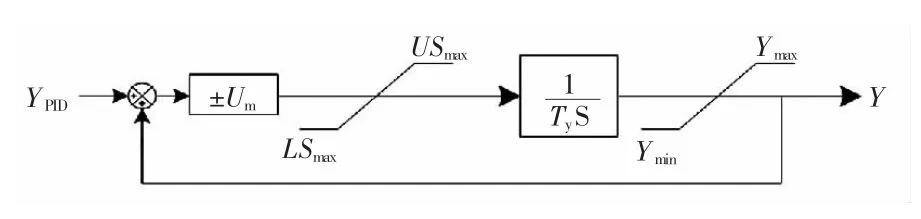
图2 执行机构计算模型Fig.2 Model of actuator

该部分仅需要对接力器响应时间常数Ty进行辨识。参数YPID为实测电子调节器输出；Um根据固有转速死区实测获得；USmax和LSmax分别根据导叶最短开启、关闭时间实测中的最短开启/关闭时间确定；Ymax和Ymin根据类型分别设定为1 和0。

3）原动机部分

原动机部分的自定义模型如图3 所示。图中Y为接力器行程，P 为原动机输出（有功功率），Tw为原动机水流惯性时间常数，P-Y 为功率-开度拟合曲线。其中P-Y 可基于出力-开度对应关系单独实测获得，该部分需要对Tw进行参数辨识。

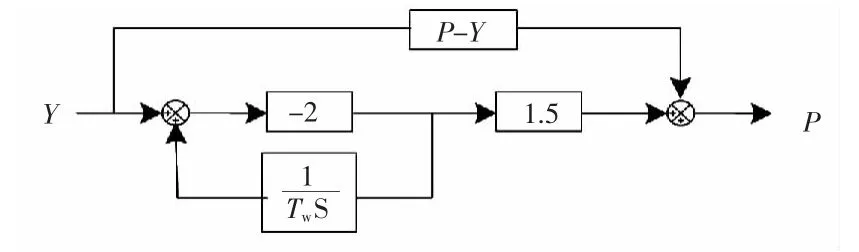
图3 原动机计算模型Fig.3 Model of original motivation

2 结合实测的调速系统辨识方法

2.1 发电机调速系统参数辨识的思路

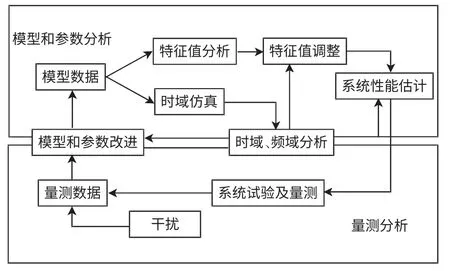
图4 发电机调速系统的参数辨识Fig.4 Parameter identification for generator speed control system

发电机参数实测包括系统静态特性试验、非并网闭环动态试验和并网闭环动态试验等多种类型。参数辨识过程如图4 所示，在输入相同激励信号下，发电机实际系统和辨识系统产生各自的响应，待辨识参数包括bt、Td、Tn、T1v、Ty、Tw等。由于某些参数容易解耦和单独辨识，可以利用传统的辨识方法进行，但对于部分参数无法单独获得输入输出量，在此种情况下，本文提出一种参数解耦辨识和整体辨识相结合的发电机调速系统参数辨识方法。该方法采用粒子群算法整体辨别，其思路是将参数辨识问题转化为求解适应度函数极值优化问题，将待辨识的物理参数设置为种群的“粒子”，根据辨识模型与实际系统输出响应建立适应度函数，按照智能优化算法的进化策略不断调整种群的“粒子”，当适应度函数超过一定阈值时，认为全局最优的“粒子”为极值问题的解，即辨识参数的最佳拟合值。

2.2 数据的预处理和参数搜索空间及适应度函数

在基于粒子群的发电机调速系统识别算法中，设m 维搜索空间中有n 个代表潜在解的粒子（x1，x2，…，xn），向量xi（xi1，xi2，…，xim）记录了第i 个粒子的位置，向量vi（vi1，vi2，…，vim）用来表示第i 个粒子的速度，根据设定的适应度函数，第i 个粒子当前所经历过的最优位置（也称个体极值）记为pi（pi1，pi2，…，pim），整个粒子群在曾经经历过的最好位置（也称全局极值）记为pg（pg1，pg2，…，pgm）（只有一个）。将每个粒子的速度和位置从第t 代迭代更新到第t+1 代，即

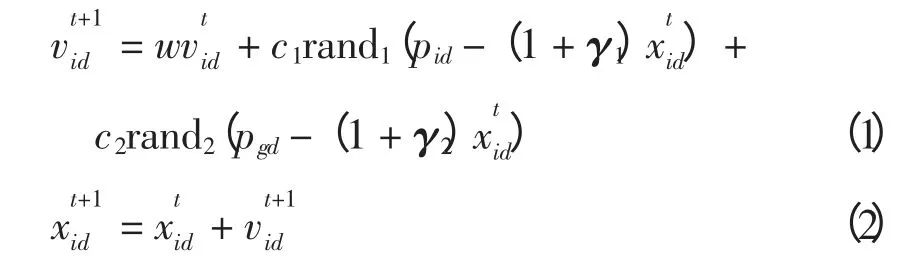
式中：i=1，2，…，n；d 为每个粒子的维数，d=1，2，…，m；w 为惯性权重常数，用来平衡算法全局和局部搜索能力；c1，c2为加速常数，其各自的取值范围通常为[0，2]；rand1，rand2为[0，1]之间相互独立的随机数。为控制进化过程中粒子留在搜索空间之中，一般需指定vmax和xmax来限制粒子的速度和位置。

优化过程中采用适应度函数，用以评价辨识模型逼近原始模型的程度，即

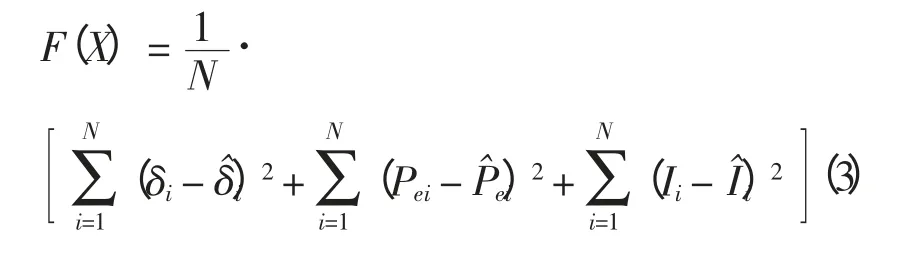
式中：δi、Pei、Ii分别为实际系统输出的发电机转子功角、有功功率、定子电流的第i 个采样值；δi、Pei、Ii分别为在模型辨识参数为X 情况下获得的仿真发电机转子功角、有功功率、定子电流的第i 个输出采样值。

值得注意的是，式（1）中γ1和γ2是随机数，在初始阶段可使得粒子群算法具有非常强的全局搜索能力。选取随机数公式为

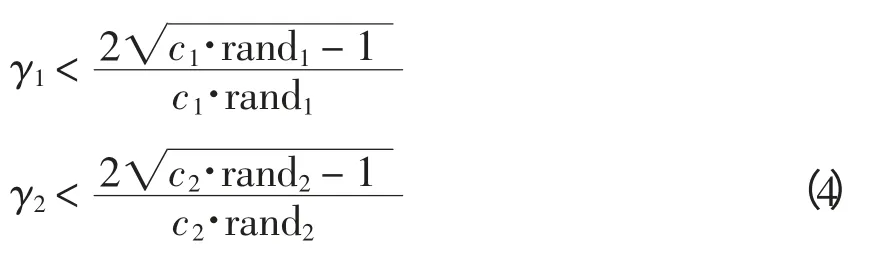
在搜索后期，可以使粒子群算法在后期能够实现渐进收敛。选取随机数公式为

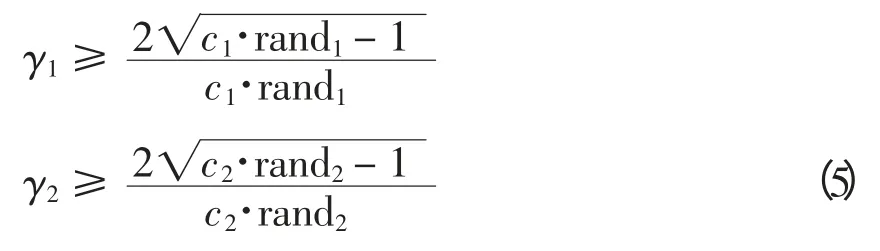
2.3 结合实测的发电机调速系统参数识别流程

结合实测过程，本文提出一种发电机调速系统解耦辨识和整体辨识相结合的辨识方法。具体步骤如下。

步骤1 基于模型库建立发电机调速系统模型，确定可变参数调速系统待优化参数。

步骤2 对具有输入输出量测数据、能够参数解耦的环节进行单独辨识，并将辨识参数带入模型中。

步骤3 对于其他难以解耦和获得输入输出数据的环节，则与已辨识参数环节组成一个整体，进行整体辨识，并基于粒子群算法来寻找最优拟合值，过程如图5 所示。

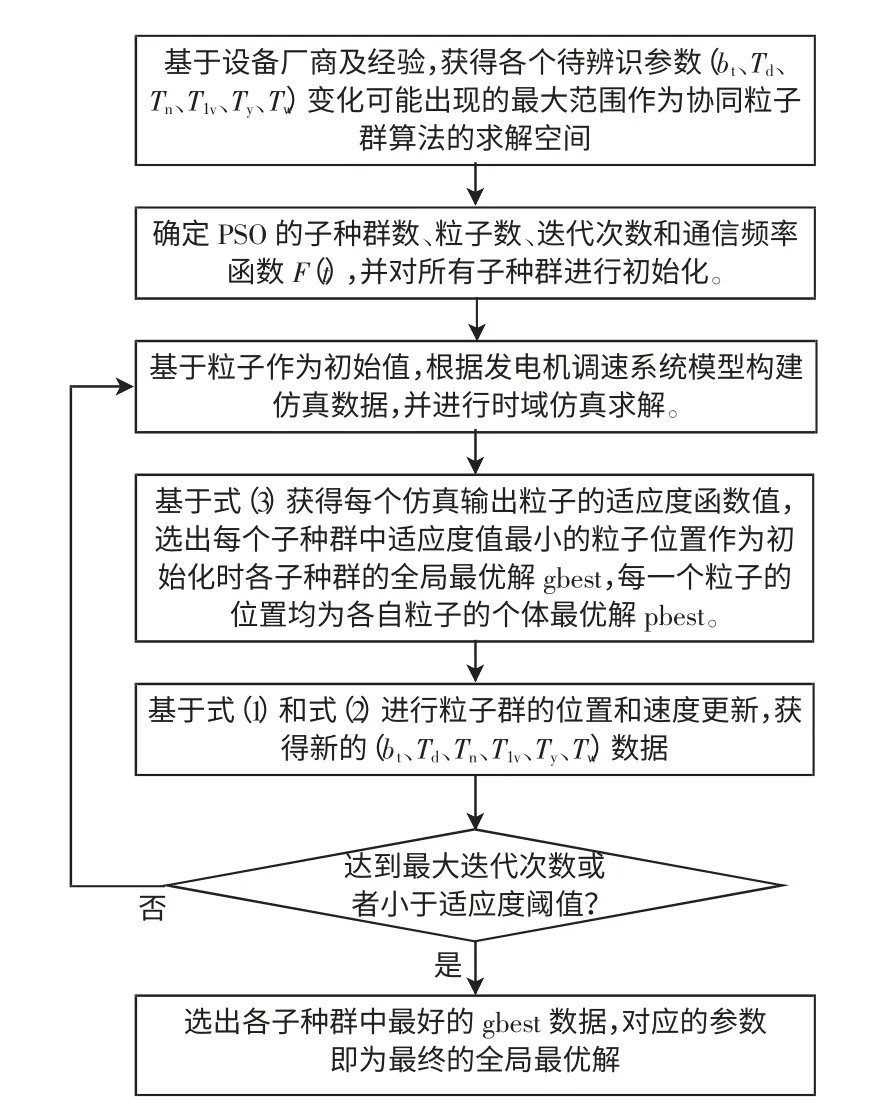
图5 基于粒子群算法的发电机调速系统整体参数辨识Fig.5 Parameter identification process based on PSO method for generator speed control system

需要注意的是，由于发电机调速器类型不同，需要整体辨识的参数内容及个数也有所不同。对于本文所给发电机模型和参数，若无法单独测量和需要整体辨识的参数为bt、Td、Tn、T1v、Ty、Tw，则可将初始化后的粒子设定为六维，即xi=[bt，Td，Tn，T1v，Ty，Tw]，每个粒子对应电气参数在求解空间中服从平均分配的随机值。而求解空间，是基于设备厂商及经验获得的待辨识参数变化可能出现的最大范围。

步骤4 对所有辨识的参数进行验证，并将实际系统作为参考模型并假设可调模型结构己知，根据可调模型与参考模型之间的输出误差进行运算。并根据运算结果，基于步骤2 和步骤3 修改可调节模型参数，使得相同输入下，可调节模型输出尽可能逼近参考模型的输出；当可调节模型输出与参考模型输出之间差别无法改善时，认为可调节模型参数即为参考模型（实际系统）参数的估计值。

为了避免算法的随机性，仿真实验分析中需要采用参数精度指标评价算法的稳定性及随机性。本文选用的参数相对误差指标定义为

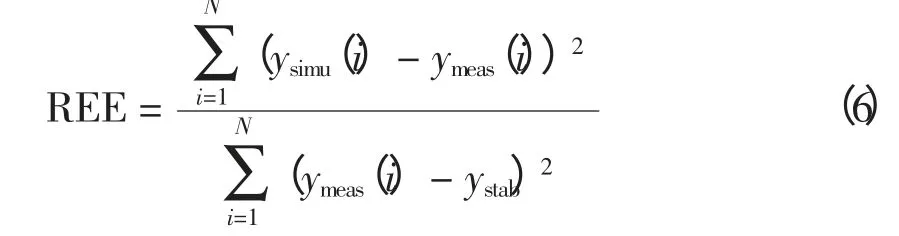
式中：ysimu（i）为仿真数据序列；ymeas（i）为实测数据序列；ystab为稳态时实测数据平均值；N 为实测数据与仿真数据的个数。该指标是一个宏观的误差指标，有比较强的物理意义，通过计算实测数据和仿真数据的偏差能量相对于实测变量扰动能量的比值，反映了一定扰动强度下，仿真误差整体值的大小。当该值接近零的时候，仿真与实测拟合较好；该值越大，误差越大。

3 算例分析

以某300 MW 发电机组调速系统模型参数辨识为例来进行说明。对某些能够获取了输入与输出数据的环节单独进行辨识，实测数据由静态试验获得。

将单独辨识获得的参数带入模型中，对不能单独测量，或者测点不全的环节进行参数整体辨识。试验条件为：调速器现地自动，一次调频投入；负载一次调频参数：bt= 30%，Td= 2 s，Tn= 0.1 s，bp=4%，ef=0.05 Hz。利用图1 所示计算模型进行仿真，其中：参数fg为实测频率，fc=1（标么值），Yc为实测开度初始值，bt= 40%，Pc为实测功率初始值，Pg为机组功率，K1、K2的端子1 和2 一直接通；辨识参数Td=1.08 s，Tn=0 s，T1v=0.15 s，bp=4.00%，ef=0.1%（标么值）。

动态调速系统实际工作情况与辨识后参数的仿真曲线对比如图6 所示，各部分实测曲线和仿真曲线基本吻合，辨识过程中参数相对误差指标REE 统计结果为0.75%，满足工程运行要求。图7给出了电网扰动情况下的实测数据记录与仿真分析曲线，由图7 可见，参数辨识后的有功功率的仿真曲线较原先的仿真曲线有较大改进，与实测曲线趋势一致，说明获得的调节系统模型辨识参数较原始参数有了较大的改进，能够更好地反映系统特性。

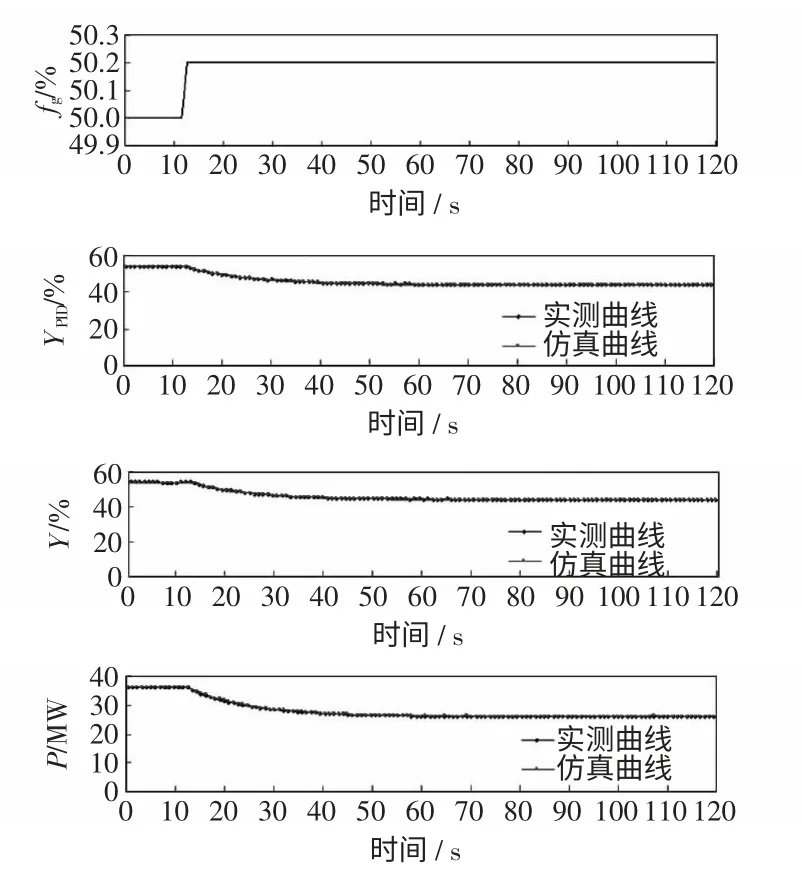
图6 频率阶跃动态调速系统实测与仿真对比Fig.6 Comparison of actual measurement and simulation output under dynamic mutation frequency

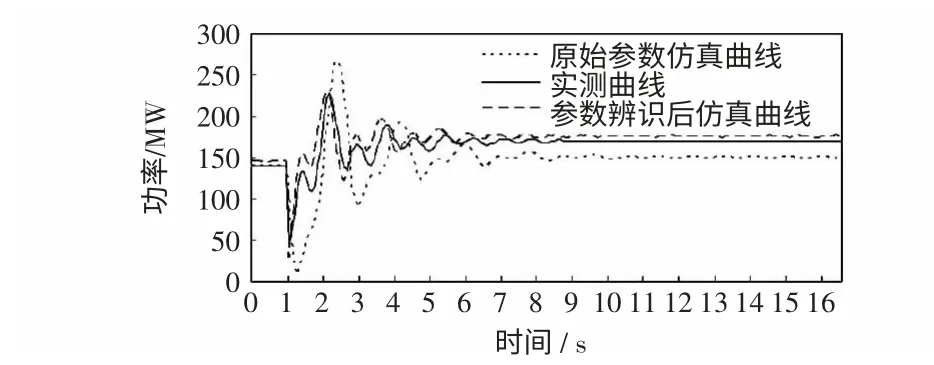
图7 电网扰动情况下测试发电机输出与仿真曲线对比Fig.7 Curve comparisons of case generator output and simulation in system fault

4 结语

电力系统中发电机调速系统的仿真模型和参数的准确程度直接关系到运行和调度的安全稳定运行水平。本文结合当前电力企业广泛开展的发电机组参数实测工作，提出一种基于粒子群算法的发电机调速系统启发式的参数辨识方法，为电力系统参数辨识技术提供一种思路和方法。

[1]寇攀高（Kou Pangao）.水轮发电机及其调速系统的参数辨识方法与控制策略研究（Study on parameters identification methods and control laws of water turbine generator and its speed governor system）[D].武汉：华中科技大学水力水电工程学院（Wuhan：School of Hydraulic and Hydropower Engineering，Huazhong University of Science and Technology），2012.

[2]Grund C E. Power system modal identification from large scale simulations using model adaptive reference control[J].IEEE Trans on Power Apparatus and Systems，1978，97（3）：780-788.

[3]汤涌，卜广全，印永华，等.PSD-BPA 暂态稳定程序用户手册[M].北京：中国电力科学研究院，2008.

[4]蔡莎莎，毛晓明，陈志勇，等（Cai Shasha，Mao Xiaoming，Chen Zhiyong，et al）.同步电机调速系统参数辨识研究进展与展望（Progress and prospect of parameter identification research on speed regulating system of synchronous generators）[J]. 广东电力（Guangdong Electric Power），2012，25（10）：28-32.

[5]唐磊（Tang Lei）.汽轮发电机组调速系统动态模型参数辨识与仿真研究（Parameter Identification and Simulation Research of the Turbo-generator Unit Speed Governor System Dynamic Model）[D].武汉：华中科技大学能源与动力工程学院（Wuhan：School of Energy Land Power Engineering，Huazhong University of Science and Technology），2009.

[6]Alonso H，Mendonca T，Rocha P. Hopfield neural networks for on-line parameter estimation [J]. Neural Networks，2009，22（4）：450-462.

[7]李鹏波，胡德文.系统辨识基础[M].北京：中国水利水电出版社，2006.

[8]潘学萍，陶正华（Pan Xueping，Tao Zhenghua）. 基于SSI-TLS 法的同步电机参数辨识（Parameter estimation of synchronous machine based on SSI-TLS）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2012，24（6）：58-61，77.