基于偏差分离的同步发电机非线性励磁控制

郭 刚，刘觉民，鲁文军，向 增，肖 乐，秦 攀

（湖南大学电气与信息工程学院，长沙410082）

改善电力系统稳定性的主要手段是控制[1]。近年来，由于非线性控制理论有了突破性的进展，微分几何方法在电力系统的非线性控制中得到了深入的研究和应用[2～3]。非线性控制理论应用于电力系统，能够明显地提高电力系统暂态稳定性，同时，对增强电压稳定性也有显著的作用[4]。然而，由于基于微分几何的反馈线性化方法需要由被控制系统的精确模型来描述系统的非线性特性，理论上这一类方法不具备对系统模型和参数不确定性的鲁棒性[5]。而在电力系统的实际运行中，存在着各种不确定性，比如稳态运行时负荷的波动、故障引起的系统拓扑结构的改变等。同时，在系统模型中也存在着不确定性，比如只能采用简化的模型和模型参数的不准确性等。

国内外学者提出了很多方法来解决上述不确定性问题，以提高控制系统的鲁棒性。如果能够得到不确定部分的界的信息，则采用鲁棒控制可以较好地处理这类不确定性[6～7]，但由于实际控制系统通常难以准确得到不确定部分的界的信息，因此设计时往往采用最坏的情况进行估计，这样会导致鲁棒控制器设计的保守性；如果不确定部分能够用参数化模型进行描述，即表示为已知的线性或非线性函数与未知参数的乘积形式，则采用自适应控制能够获得较好的控制效果[8～9]。然而，自适应控制中的参数自适应律设计复杂，采用的backstepping 方法设计步骤较多，计算量大，不利于工程实现。

不同于非线性H∞控制、自适应控制、滑模变结构控制等其他非线性控制方法，本文基于坐标变换和状态反馈精确线性化的微分几何理论，在考虑不确定性偏差的前提下，提出一种新的非线性控制策略，以改善上述此类方法的鲁棒性，进而将其应用于同步发电机励磁控制器的设计中，以验证其对电力系统干扰的抑制效果。

1 基本控制原理

计及模型偏差和扰动偏差的非线性系统的状态空间表达式为

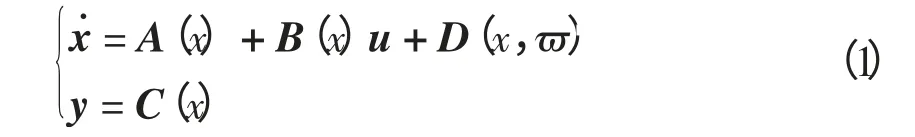
式中：状态量x∈Rn；干扰量ϖ∈Rn；控制量u∈Rm；输出量y∈Rm；A（·）、B（·）、C（·）、D（·，·）均为相应维度的光滑映射，其中D（x，ϖ）为由建模及干扰引起的模型偏差量。一般地，可选择输出量为状态量的线性变换，从而输出量包含状态量的全部或部分信息，故式（1）可表示为

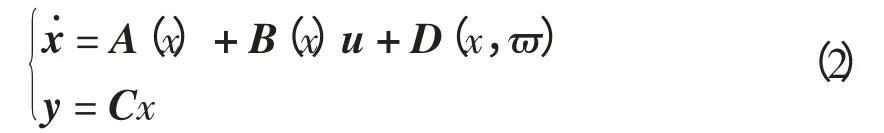
式中，C 为常数矩阵。不失一般性，考虑m＜n 时，若存在坐标变换

使得上述非线性系统化为

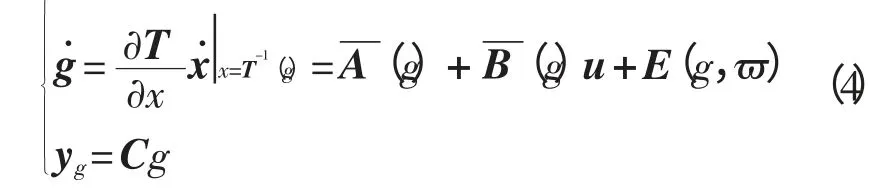
其中：

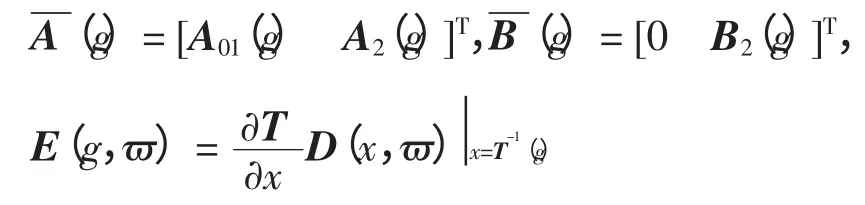
从而，有

还可写为

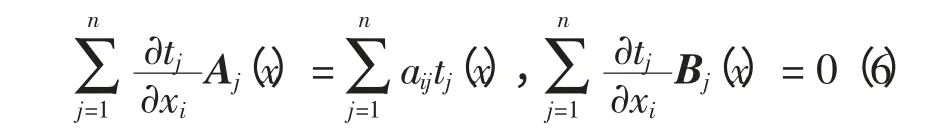
其中，i∈（n-m）。又有

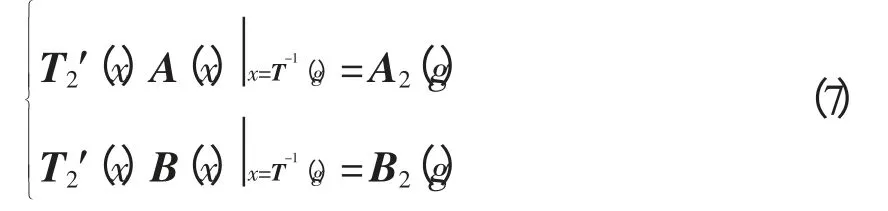
得部分线性化的系统状态方程为

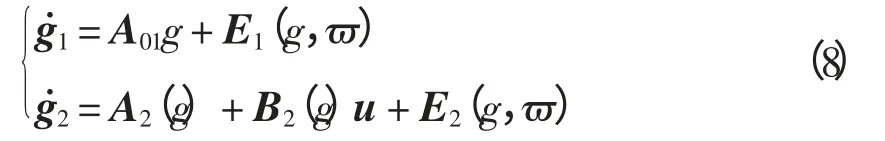
设存在非线性状态反馈控制量

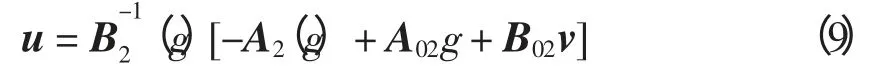
使得方程组（8）中第2 个公式线性化，即

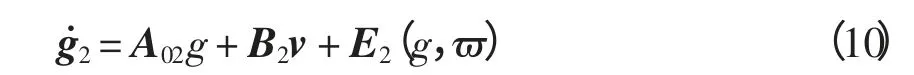
则式（2）线性化为

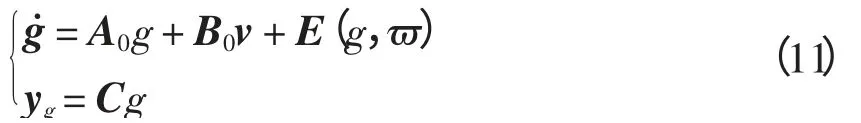
式（3）～式（11）中：状态量g∈Rn，g1∈Rn-m，g2∈Rm；v为预控制量；A2（·）、B2（·）、E（·，·）、E1（·，·）、E2（·，·）分别为对应维数的光滑映射；A0、B2、A01、A02、B02分别为相应阶数的常数矩阵；E（g，ϖ）= [E1（g，ϖ），E2（g，ϖ）]T，B0=[0，B02]T，A0=[A01，A02]T。不妨设v=vp+vq，利用线性最优控制理论设计控制变量vp（t），即

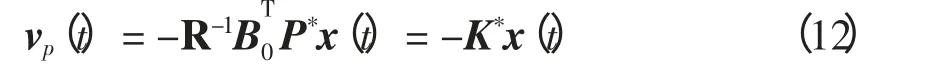
式中，P*是Riccati 矩阵方程的解。从而，式（11）可化为

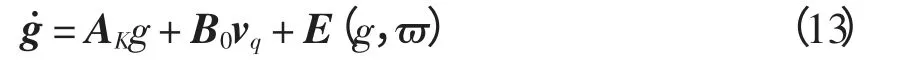
其中：AK=A0-B0K*。构造标称线性系统为

分离出偏差量E（g，ϖ），即

补偿控制量vq（t）为

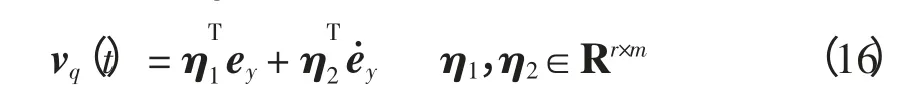
使其满足

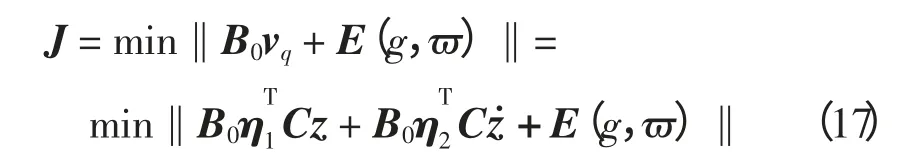
即

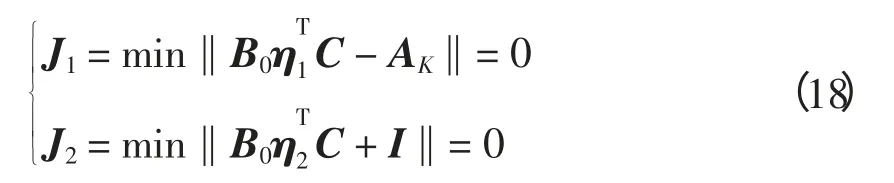
则最小二乘解为

综上，得到最优控制量vp（t）和补偿控制量vq（t），从而可设计原非线性系统的控制量u。上述结论可归结为以下命题。

命题1 非线性系统（式（2）），通过坐标变换（式（3））和状态反馈（式（9））化为线性系统（式（11））的充要条件是：式（6）成立，且B2（x）在（x，v）的邻域Ω 内非奇。此时，状态反馈控制量u 为

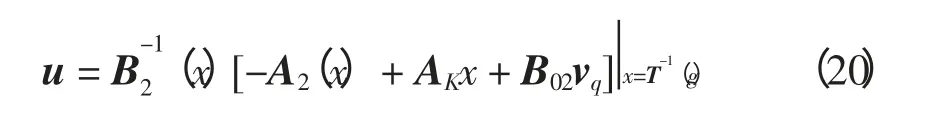
以此得到：按照所设计的非线性反馈控制律，控制量u 包含3个分量，即u = uo+ up+ uq，其中：，抵消非线性，综合线性最优，消除不确定性偏差。

2 非线性励磁控制器设计

单机无穷大系统如图1 所示，同步发电机通过变压器和输电线路连接到无穷大电网。含偏差量的系统模型可表示为

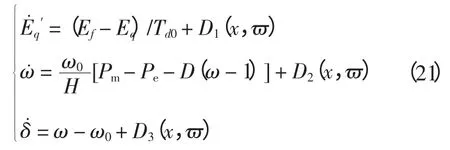
其中：

式中：Pm为机械功率，仅考虑励磁控制，假定机械功率恒定；D1（x，ϖ）、D2（x，ϖ）、D3（x，ϖ）分别为电磁扰动、转矩扰动、频率扰动及建模偏差，且均为标量函数；其他符号的电气意义可参见文献[1]。

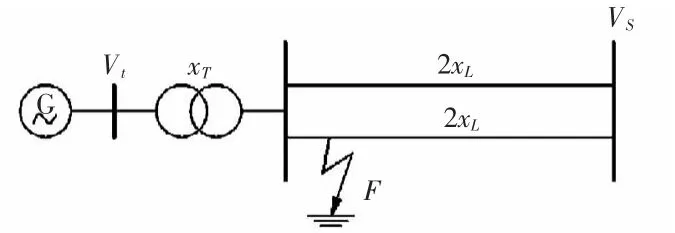
图1 单机无穷大系统Fig.1 Single-machine-infinite-bus power system

令控制量u=Ef；状态量x=[，ω，δ]T；初始状态量则单机无穷大系统状态方程为

输出信号为

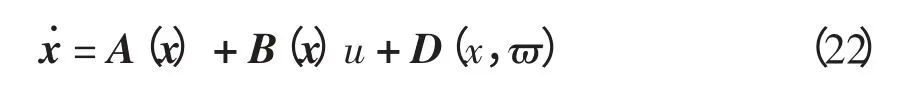
由命题1 构造非线性状态反馈控制量式（20）和坐标变换

将原非线性控制系统转化为线性控制系统式（11）。进而，由命题1 可得到非线性控制系统的控制变量u。

3 系统仿真实验

采用PSCAD/EMTDC 仿真，以检验第2 节提出的基于偏差分离的非线性励磁控制器对扰动的抑制效果。SMIB 系统的参数为= 3.2 s，0.053 s=0.1 s，xT=0.083 p.u.，xd=1.305 p.u.，xq=0.474=0.296 p.u.=0.252 p.u.=0.243 p.u.，xL=0.183 2 p.u.，H=3.2 s，D=2.0 p.u.，p=16。系统运行点为：δ0= 19.4°，Pm= 0.75 p.u.，Vs= 1.0 p.u.。励磁电压限幅为|Ef|≤6 p.u.。

控制器涉及的相关参数经由计算得：B02=1，K*=[-1 -2.29 -2.14]，vq（t）=-ey-

对基于能量函数的非线性鲁棒励磁控制器[3]和传统PID 励磁控制器进行仿真。图1 所示故障情况为：系统从平衡点开始运行，t=0.1 s 时，输电线路首端发生三相接地故障，t=0.2 s 时保护装置动作，故障线路被切除；t=0.4 s 时故障消失，重合闸成功。动态仿真结果如图2 所示。

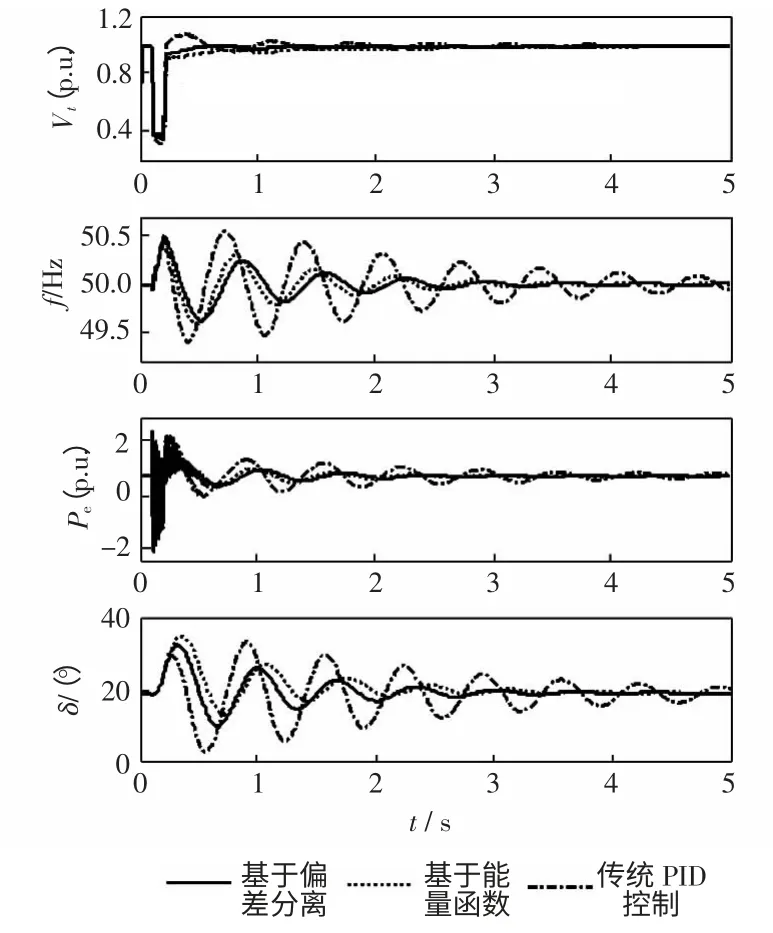
图2 系统仿真响应曲线Fig.2 Responses of system

由图2 可以看出，较之于传统PID 控制和基于能量函数的非线性鲁棒控制，在本文所提出的控制律作用下，系统发生大扰动后发电机的转子角度、转子角频率、发电机端电压和输出有功功率均可以更迅速地过渡到系统平衡状态，并能够保持系统的稳定性。

4 结语

本文基于微分几何的坐标变换和状态反馈精确线性化方法，在考虑干扰、系统模型及参数不确定性的前提下，提出了一种基于偏差分离的非线性控制策略。不同于非线性H∞控制、自适应控制、滑模变结构控制等其他非线性控制方法，该策略采用偏差分离结构在线获取系统的偏差量信息，从而改进了此类非线性控制方法的鲁棒性，给出了控制变量的构造方法和一般表达式，进而将其应用于电力系统励磁控制器的设计。利用PSCAD/EMTDC 仿真得到的结果表明该控制器对于扰动的抑制效果明显优于传统PID 控制，与基于能量函数的非线性鲁棒控制器相比较，在系统暂态稳定性方面也具有一定的优越性。

[1]卢强，梅生伟，孙元章.电力系统非线性控制[M].2 版.北京：清华大学出版社，2007.

[2]吴青华，蒋林（Wu Qinghua，Jiang Lin）.非线性控制理论在电力系统中应用综述（Survey on nonlinear control theory and its applications in power systems）[J]. 电 力系统自动化（Automation of Electric Power Systems），2001，25（3）：1-10.

[3]马进，席在荣，梅生伟，等（Ma Jin，Xi Zairong，Mei Shengwei，et al）.基于Hamilton 能量理论的发电机汽门与励磁非线性稳定控制器的设计（Nonlinear stabilizing controller design for the steam -valving and excitation system based on Hamiltonian energy theory）[J].中国电机工程学报（Proceedings of the CSEE），2002，22（5）：88-93.

[4]孙元章，卢强，孙春晓（Sun Yuanzhang，Lu Qiang，Sun Chunxiao）. 电力系统鲁棒非线性控制研究（On the study of power system nonlinear robust control）[J].中国电机工程学报（Proceedings of the CSEE），1996，16（6）：361-365.

[5]Isidori A.Nonlinear Control Systems[M].3rd ed. Berlin：Springer-Verlag，1995.

[6]Sun C，Zhao Z. Design of nonlinear robust excitation control for multi -machine power systems [J]. IEE Proceedings -Generation，Transmission and Distribution，1996，143（3）：253-257.

[7]梅生伟，黎熊，卢强，等（Mei Shengwei，Li Xiong，Lu Qiang，et al）.基于反馈线性化方法的励磁系统非线性H∞控制研究（Nonlinear H∞control for excitation systems via feedback linearization method）[J]. 电力系统及其自动化学报（Proceedings of the CSU-EPSA），1999，11（4）：1-7.

[8]王康，兰洲，甘德强，等（Wang Kang，Lan Zhou，Gan Deqiang，et al）.非线性系统自适应控制及其在电力系统中的应用（A survey on adaptive control of nonlinear systems and its application in power systems）[J]. 电网技术（Power System Technology），2007，31（11）：11-16.

[9]Wang Jie，Chen Chen，La Scala Massimo.Parametric adaptive control of multimachine power systems with nonlinear loads[J]. IEEE Trans on Circuits and SystemsⅡ，2004，51（2）：91-100.