基于有向图的网损分摊机理分析与建模
胡福年,刘亚军,胥 璐
(江苏师范大学电气工程及自动化学院,徐州221116)
电力市场中,每个用户都应该承担网损责任,而不同的分摊法又会产生很大的影响。英国电力市场运行的实践表明,不同的分摊方案对交易电价的影响可能高达10%[1~2]。由于交流电路中的功率不能应用线性叠加原理进行直接解耦运算,目前任何的网损分摊方案都只是某种原则的近似。网损分摊方法有很多种[3~4],具有代表性的方法有平均网损分摊法[5]、合同路径法[6]、边际网损系数法[7~9]、潮流跟踪法[10~14]、基于shapley 值分摊法[15~16]等,这些方法各有优劣。
本文在前期研究工作的基础上[17],应用运筹学中的多目标规划方法和有向图理论对网损分摊方法做了进一步研究。
1 比例分配原则
比例分配原则的思想是:假定输电节点是个理想的潮流混合器,潮流在各个节点上按照比例分配的原则分布[10],如图1 所示。

图1 比例分配原则Fig.1 Proportional sharing principle
图1 中,j,k为注入支路,m,l 为输出支路。则比例分配原则公式为
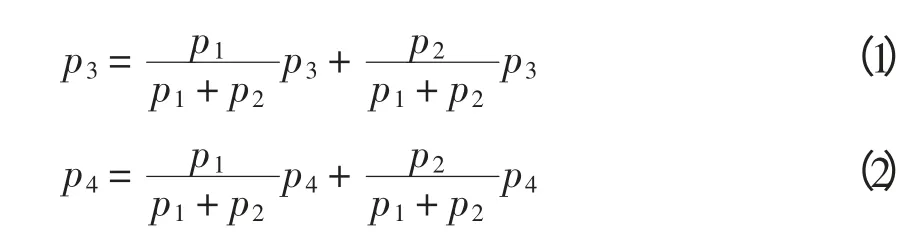
文献[18~19]应用电路理论中的叠加原理对比例分配原则进行了证明。由于叠加原理只适用于线性电路,而电力系统是典型的非线性电路,因此,该分配原则的理论探讨还需进一步深化。文献[20]采用博弈论和信息论从经济的角度对该原则进行了证明。
在假定输电节点是个理想的潮流混合器的基础上,本文提出另外的证明方法,以说明它是合理的分配理论。
将式(1)和式(2)变形为
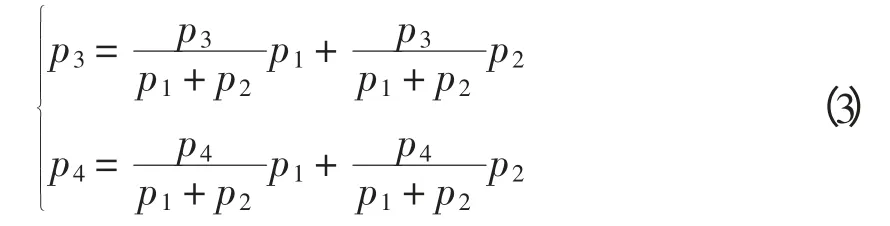
将问题转化为求线性方程组系数α1,β1,α2,β2的形成,即
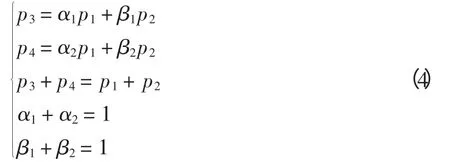
式中,只要知道p3或p4的任一值,另一个值就可以求出。可以认为α1,β1之间及α2,β2之间存在竞争关系,值越大越好,故这个问题是一个多目标规划问题[21]。
利用式(4)建立的多目标决策模型为
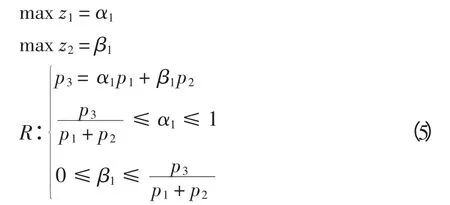
考虑到p1+p2= p3+ p4,p1≥p2,p4≥p3,则
2p3≤p3+ p4=p1+p2 ≤2p1 ⇒p3 ≤p1
故对于该模型,又存在以下2 种情况。
1)p1≥p3≥p2,p4≥p3
步骤1 分别求2 个单目标规化问题max Z1和max Z2,解得


相应的目标值为

步骤2 作出z 的值表,见表1。

表1 z 的值Tab.1 Value of z
根据表0 中z 的数据,可计算得到γ1=1,γ2=0。于是求得权系数为ω1=1,ω2=0。
步骤3 问题转化为线性规划问题

当λ 取得最小值时,

2)p1≥p2≥p3,p4≥p3
同理可得:γ3=1,γ4=0;ω3=1,ω4=0。
将问题转化为线性规划问题,即
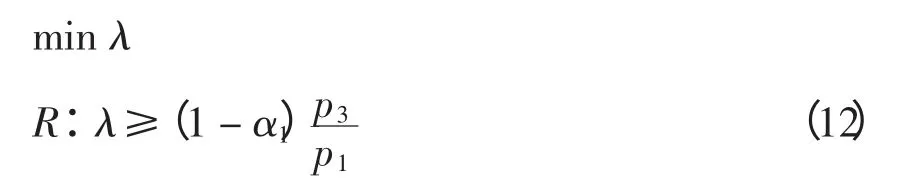
结果显然与情况1)相同。
再利用式(4)建立多目标决策模型,即
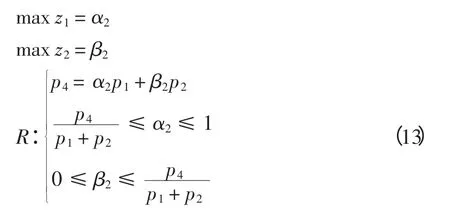
考虑到

则
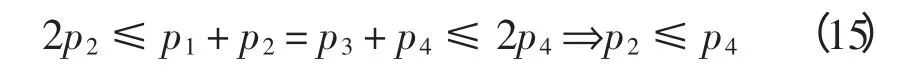
故对于该模型,又存在以下2 种情况。
1)p1≥p4≥p2,p4≥p3
同上面的解法可得:γ5=1,γ6=0;ω5=1,ω6=0。问题转化为下面的线性规划问题,即

λ 取得最小值时,解之得
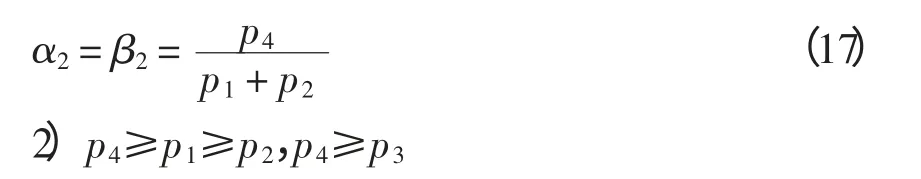
同上面的解法可得:γ7=1,γ8=0;ω7=1,ω8=0。问题转化为线性规划问题,即

故式(4)在多目标规划下的最优分配方案为

将α1、β1看作2 个争取利益最大化的竞争者,作出博弈曲线,如图2 所示。
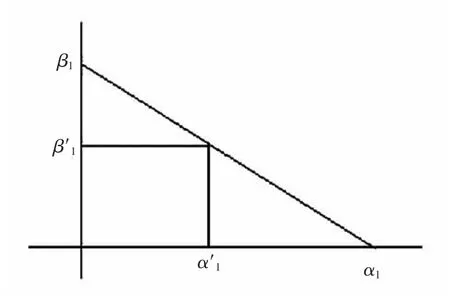
图2 双方的博弈曲线Fig.2 Game curve of the two sides
由图2 可以看出,当且仅当α1=β1时达到唯一的均衡点。从以上的证明中可以看出比例分配原则的实质是平等分配的思想,故认为该方法是可行且合理的。
2 域
2.1 域的定义
定义2.1 在有向图中,对任意给定的有向母线(边)l 的终点tl和某个终端用户ui而言,如果至少存在一条以tl为起点、ui为终点的有向路,则称ui为l 的用户元素,l 的所有用户元素ui组成的最大集合称为l 的域,记为Dl。在此认为,对其他母线(边)l′而言,Dl中的所有用户元素都是等价的,故在Dl中分摊l′的网损时,可以对Dl中的用户元素进行平均分摊,如图3 所示。图中箭头方向表示潮流的流向,用户记为Ui,交易量记为

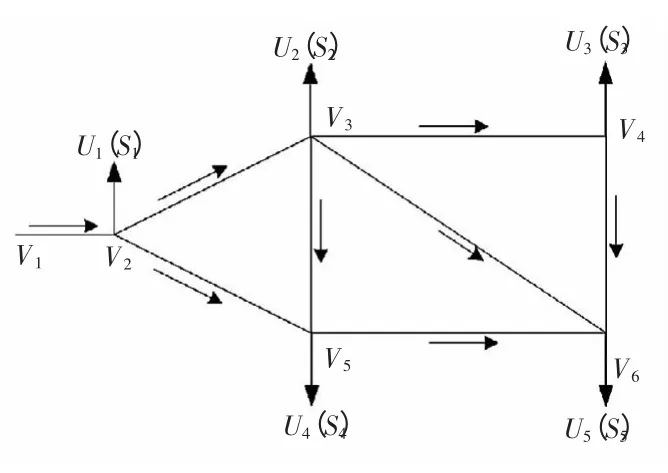
图3 有向图Fig.3 Directed graph
从对域的定义中可以看出流进同一节点的有向边有相同的域,故认为这些有向边是属于同一类。这样就可通过观察各个节点的入度并使用划线删除法将所有有向边进行分类,极大地减少计算量。图3 中所有的域可以分为5 类:

2.2 域的算法
定义2.2 如果有向图D(V,X),V={v1,v2,…,vn}和(0,1)A=(aij)有一一对应关系,即
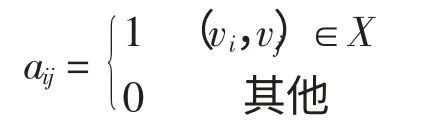
则称A 为有向图D(V,X)的n 阶邻接矩阵,记为A(D)。反之,任一给定一个(0,1)方阵A,也就对应一个有向图D(A),D(A)称为A 的伴随有向图。
在有向图3 中,

定理2.2 在A 的幂序列I,A,A2,A3…中必然要出现相等的项,且从某第k+1 项Ak起,A 的幂序列将按某个周期作周期性变化[22]。
假设有向图有n 个节点,其中有m 个节点直接与用户相连。算法步骤如下。
1)准备工作
(1)依据有向图和各节点的入度,将所有的有向边进行分类,建立有向边分类表;
(2)依据与用户直接相连的节点优先编号的原则,对所有的节点进行统一编号;
(3)写出邻接矩阵A。
2)算法流程(见图4)
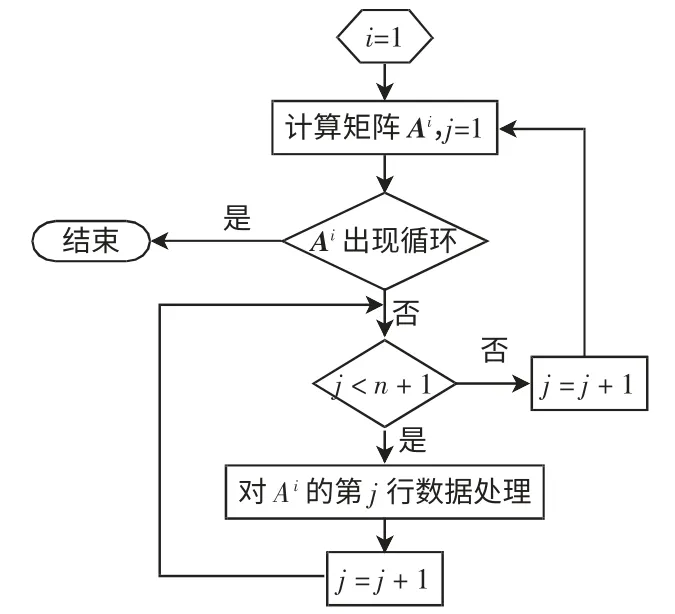
图4 域的算法流程Fig.4 Flow chart of domain algorithm
3)流程图说明
(1)判断Ai是否已经开始循环,根据秩(An)≤秩(An-1)≤…≤秩(A)和定理2.2,可以计算每个Ai的同时也记录下它们所对应的秩,则这个序列是单调不增的。先判断秩(Ai)和秩(Ai-1)是否相等,若不等则说明还没有出现循环;若相等则在所有与秩(Ai)相等的Aj(j (2)对Ai的第j 行数据进行处理。 依据前面对节点编号的原则,取一节点vk,则节点vi(i=1,2,…,m)有用户ui(i=1,2,…,m)与之直接相连。 定义2.3 由定理2.2 知,若vk到vi之间没有长为l 的途径,则 换言之,若vk到vh,h∈[1,m]之间没有有向通路,则无论迭代多少次,向量中的第h 个元素始终为0。 若vk到vh,h∈[1,m]之间有有向通路,则经过有限迭代后,第h 个元素变成大于0,至于值是多少无关紧要。 以此类推。建立所有节点与vh,h∈[1,m]的有向道路表。最后查有向边分类表和有向路径表,就可以得到每条有向母线(边)的域。 计算图3 中母线lv1v2上的网损分摊问题,作出Dlv1v2所有元素构成的无向图,如图5 所示。 图5 无向图Fig.5 Undirected graph 首先,利用交叉项分摊理论将网损分摊给U1、支路和支路v2v5(记为 设有一个网络结构如图6 所示,包含n 条注入母线,k 个交易,但仅有一个公共节点N。其中每条母线的潮流为Si=Psi+jQsi(i=1,2,…,n),线路阻抗为Zi=Ri+jXi(i =1,2,…,n),每个交易量为Ti=Pti+jQti(i=1,2,…,k)。这个结构图包括了所有单节点的潮流流向图,图中箭头的方向表示潮流的流向。 图6 网络结构Fig.6 Network structure 分析如何分摊与节点N 相连的母线的网损(线损)问题。首先依据已经证明过的比例分配原则将该网络拆分为n 个由单母线、k 个交易组成的网络结构,如图7 所示。其中: 其次对其中第i 个结构进行分析,计算母线li的线损ΔSli,即 图7 网络拆分Fig.7 Network split 理论上,任一电网经过潮流计算后,都可以看成一个有向图,网损分摊的算法流程如图8 所示。 图8 网损分摊的算法流程Fig.8 Flow chart of loss allocation algorithm 采用文献交叉项分摊方法,以IEEE 5 节点网络为例,比较和验证本文采用方法的合理性。线路参数和负荷(电压采取标幺值1,功率的单位为MW)如图9 所示。网损分摊结果如表2 所示。 从表2 可知: (1)网损的分摊不仅与自身的交易幅值有关,还与输送距离、实际的物理潮流有关; (2)该算法同时考虑有功功率和无功功率,没有忽略有功和无功功率的相互作用对网损的影响,计算更合理准确; (3)该算法根据各支路的交易潮流来计算,可以避免交叉项的交叉补贴; (4)该算法计算的网损分摊值不会出现负值,且与交易顺序没有关系。 网损分摊方法直接影响电力市场各参与方的经济利益和效益,其公平性与合理性一直受到广泛的关注。针对网损分摊这一问题,本文从博弈论和信息论从经济的角度出发,将网损分摊转化为多目标规划问题,应用运筹学中的多目标规划优化方法,证明了其合理性。为了更加合理地进行网损分摊,本文给出了一种基于有向图的网损分摊算法。首先结合组合矩阵和有向图理论和性质给出了域的定义及查找算法,进而给出了一种基于有向图的网损分摊算法,并以IEEE 5 节点系统为例进行算例分析,其结果表明了该方法的合理性和可行性。对于复杂电力系统网络,对其进行网络拆分后,本文的研究结果也同样适用。 表2 网损分摊结果Tab.2 Loss allocation results MW 图9 IEEE5 节点Fig.9 IEEE 5 nodes [1]杜正春,夏道止(Du Zhengchun,Xia Daozhi).输电系统网损的合理分摊(A novel method for allocation of transmission losses)[J].电力系统自动化(Automation of Electric Power Systems),2002,26(4):18-22. [2]Shuttleworth,W I. Allocation Transmission Losses:Methods and Criteria[C]//A Submission to the DICG Prepared by NERA.London England:1999. [3]鲁广明,鲍海,杨以涵,等(Lu Guangming,Bao Hai,Yang Yihan,et al).输电网网损分摊方法的比较研究(Study of transmission loss allocation methods)[J]. 华东电力(East China Electric Power),2008,36(5):37-40. [4]董世勇,倪广魁(Dong Shiyong,Ni Guangkui).电力系统网损分摊方法研究(Discussion on loss allocation method for power system)[J]. 四川电力技术(Sichuan Electric Power Technology),2010,33(3):6-10,46. [5]杜松怀,温步壕,蒋传文.电力市场[M].北京:中国电力出版社,2004. [6]Baldick R,Kahn E.Contract paths,path-shifters,and efficient electricity trade [J]. IEEE Trans on Power Systems,1997,12(2):749-755. [7]Conejo A J,Arroyo J M,Alguacil N,et al. Transmission loss allocation:A comparison of different practical algorithms[J]. IEEE Trans on Power Systems,2002,17(3):571-576. [8]伍期刚,程浩忠,刘梓洪(Wu Qigang,Cheng Haozong,Liu Zihong).边际网损系数法中的网损分摊调整方法(New regulation method of marginal loss coefficient in loss allocation of power market)[J]. 电力系统及其自动化学报(Proceedings of the CSU-EPSA),2005,17(3):78-81. [9]艾东平,鲍海,杨以涵(Ai Dongping,Bao Hai,Yang Yihang).基于电路理论的发电权交易网损增量补偿解析(Analysis of incremental loss compensation on generation rights trade based on circuit theory)[J].电力系统保护与控 制(Power System Protection and Control),2010,38(22):135-140. [10]Bialek J.Tracing the flow of electricity[J].IEEE Proceedings-Generation,Transmission and Distribution,1996,143(4):313-320. [11]Wu Z Q,Chen G Z. MVA power flow and loss analysis for electricity market[J].IEE Proceedings-Generation,Transmission and Distribution,2001,148(2):153-158. [12]谢开贵,周家启(Xie Kaigui,Zhou Jiaqi).基于有向通路的潮流跟踪新方法(A new power flow tracing method based on directed path)[J].中国电机工程学报(Proceedings of the CSEE),2001,21(11):87-91,95. [13]Chai Soon-Kin,Sekar A.Graph theory application to deregulated power system [C]//33rd Southeastern Symposium on System Theory.Athens,USA:2001. [14]龚卫国,张伟民(Gong Weiguo,Zhang Weimin).基于有向通路的潮流跟踪新算法(A new power flow tracing method based on directed circuit)[J].电测与仪表(Eletrical Measurement & Instrumentation),2011,48(542):54-57. [15]Tan X,Lie T T.Application of the shapley value on transmission cost allocation in the competitive power market environment[J]. IEE Proceedings-Generation,Transmission and Distribution,2002,149(1):15-20. [16]胡朝阳,韩祯祥(Hu Zhaoyang,Han Zhenxiang).基于Shapley 值的网损分摊新方法(A new Shapley value based method for allocation of transmission losses)[J]. 电力系统自动化(Automation of Electric Power Systems),2003,27(7):32-35. [17]胡福年,刘亚军,胥璐(Hu Funian,Liu Yajun,Xu Lu).基于同胚映射和微元分析的网损交叉项分摊方法研究(Research on the cross item allocation of power losses based on homeomorphism mapping and microelement methods)[J].电力系统保护与控制(Power System Protection and Control),2012,40(19):96-102. [18]刘福斌,李扬,陈珩(Liu Fubin,Li Yang,Chen Heng).电力市场中按比例分配原则的证明及其推广(Proof and extension of proportional sharing principle in electricity market)[J].电网技术(Power System Technology),2001,25(5):25-29. [19]Wu Z Q,Chen Z G. MVA power flow and loss analysis for electricity market[J]. IEE Proceedings-Generation,Transmission and Distribution,2001,148(2):153-158. [20]Bialek J W,Kattuman P A. Proportional sharing assumption in tracing methodology[J]. IEE Proceedings-Generation,Transmission and Distribution,2004,151(4):526-532. [21]钱颂迪.运筹学[M].北京:清华大学出版社,1990. [22]柳柏濂.组合矩阵论[M].北京:科学出版社,1996.
2.3 实例计算
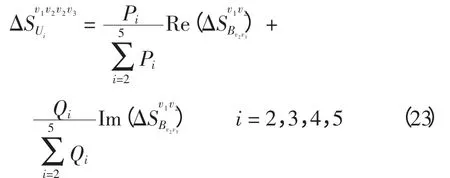
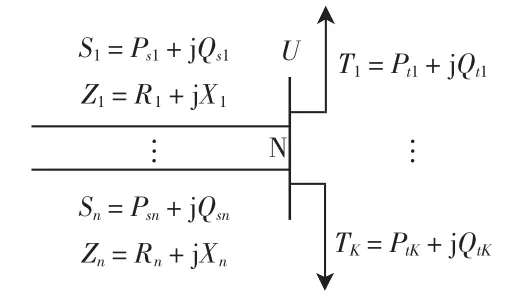
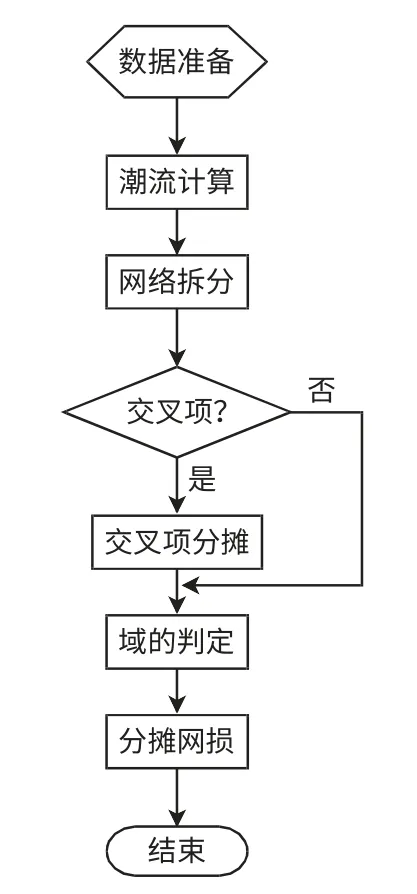
3 网损分摊的算法
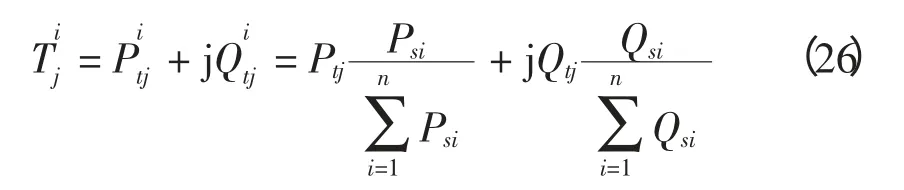

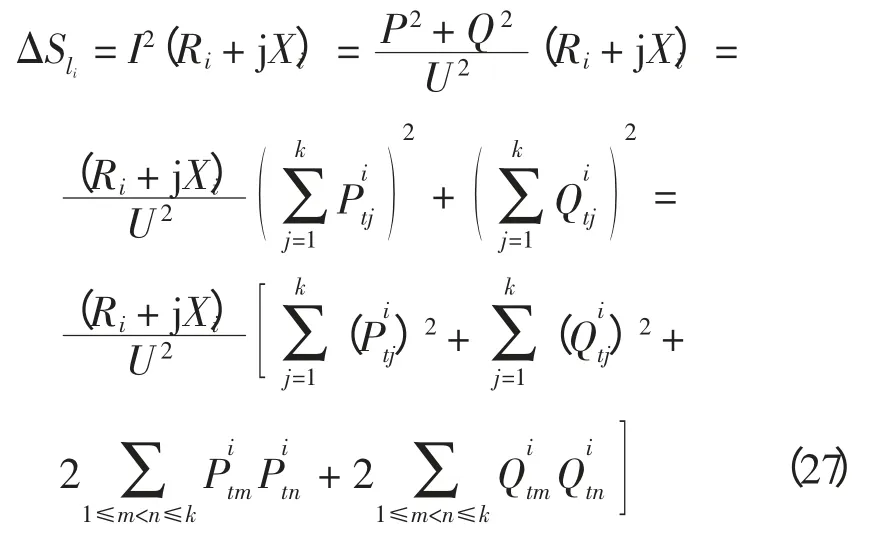
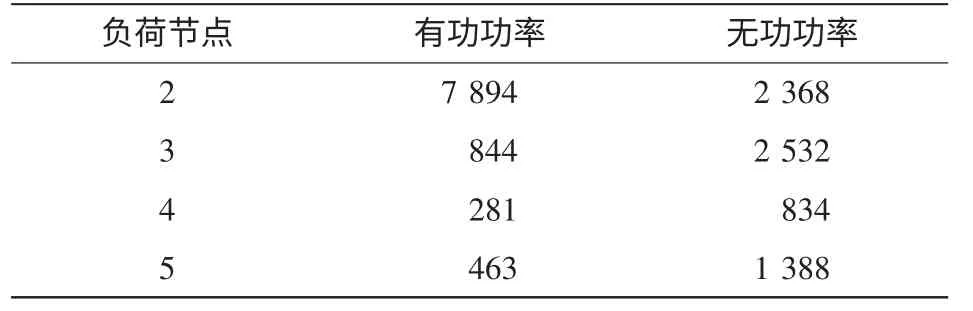
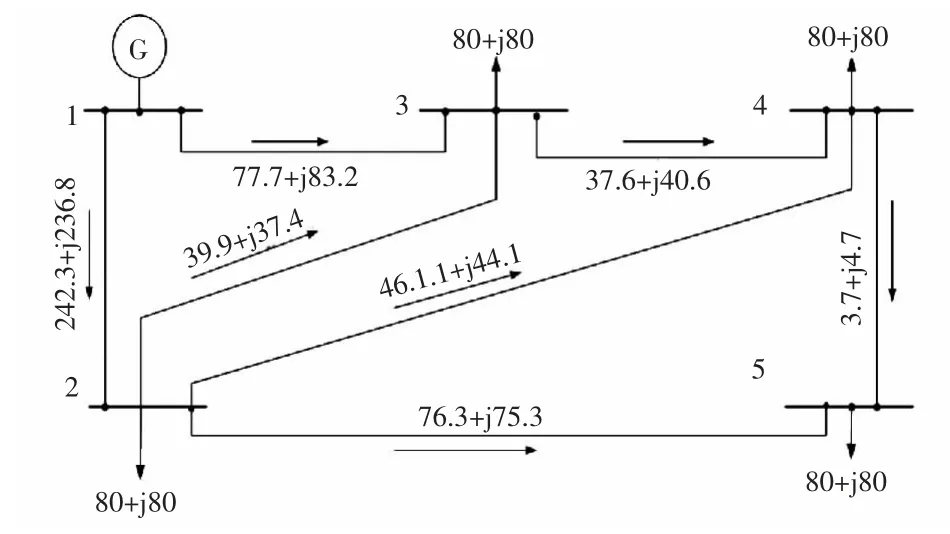
4 仿真计算
5 结语