直驱式波浪发电系统的输出功率平滑控制策略

李 凯，吴 峰，秦 川，鞠 平

（1.河海大学能源与电气学院，南京211100；2.可再生能源发电技术教育部工程研究中心，南京210098）

波浪能是清洁的可再生能源，开发和利用海洋波浪能对缓解能源危机和环境污染问题具有重要的意义。近年来，波浪发电技术取得了长足的进步，各国研究人员开发了多种不同的波浪发电装置[1]，其中，直驱式波浪发电系统具有结构简单、能量转换效率高的特点，是最有前景的波浪发电系统之一。

直驱式波浪发电系统通常采用直线永磁发电机LPMG（linear permanent magnet generator）将波浪能转换为电能，由于波浪随时间连续变化，输出功率将波动，因此，必须对波浪发电系统的输出功率进行平滑，从而满足并网运行的要求。直驱式波浪发电系统通常通过背靠背变换器并网运行，文献[2～3]采用背靠背变换器的并联电容器作为储能元件对直驱式波浪能发电系统的输出功率进行平滑，电容器进行储能要求其容量较大，大电容的体积很大，难以实际应用；文献[4]应用电池储能平滑直驱式波浪发电场的输出功率，设计了嵌入式和集中式2 种拓扑结构，取得了比较好的结果，但是，在控制电池储能吸收的实时功率时，需要知道波浪能发电系统的平均功率，由于波浪的幅值和周期随机波动，平均功率难以获取。

本文基于低通滤波原理和波电功率预测技术，分别提出2 种直驱式波浪发电系统输出功率的平滑策略，并通过仿真分析，验证了所提出功率平滑策略的有效性。

1 直驱式波浪发电系统原理

阿基米德浮子AWS（Archimedes wave swing）是第一个采用直驱技术的波浪发电系统，为了更好地说明直驱式波浪发电系统的原理和所提出的功率平滑策略，本文以AWS 为例进行阐述。

AWS 的结构如图1 所示，AWS 的底部固定于海底，气缸当中充满了密封气体。当波浪来临时，由于水的重力作用，浮子向下运动，同时气缸中的空气压力增大；当波浪谷到达AWS 顶部时，顶部水的重力减小，气缸中的气压大于外部的水压，浮子向上运动，这样浮子上下往复运动[5]。

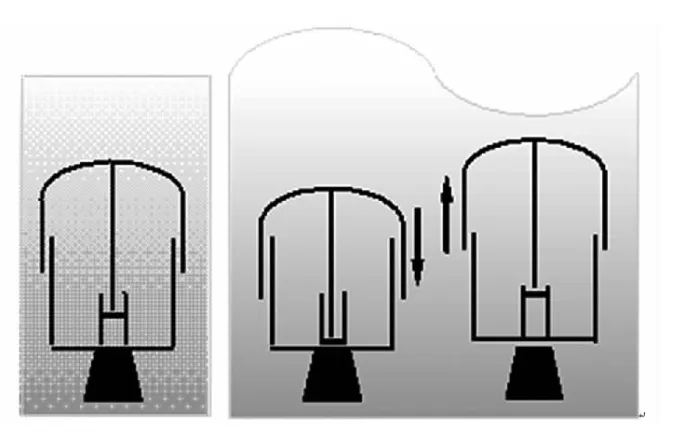
图1 AWS 结构图Fig.1 Configuration of AWS

AWS 浮子与LPMG 的动子直接相连，将浮子的动能转化为电能。由于动子上下往复运行，其运动速度的大小和方向都是变化的。因此，LPMG 的感应电动势、端口电压和定子电流的频率和幅值变化，AWS 的输出功率也随之变化。

在规则波浪条件下，LPMG 在dq 坐标下的感应电动势和定子电流为

则LPMG 的输出功率为

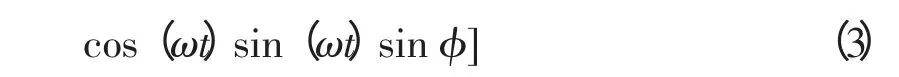
可见，波浪发电机输出功率的振荡频率是感应电压频率的2 倍。因此，波浪发电系统必须通过背靠背变换器与电网相连，并网结构如图2 所示。本文应用储能设备对AWS 输出功率进行平滑，设计相应的功率平滑控制策略。

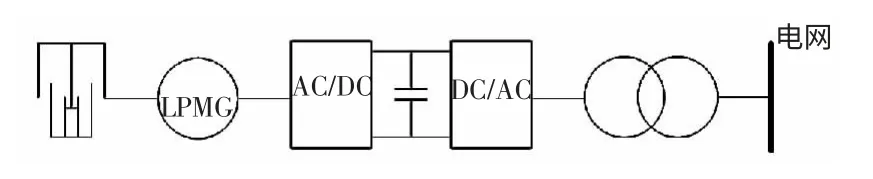
图2 AWS 直驱式波浪能发电系统并网结构Fig.2 Structure of AWS-Based DDWECS integrated into power grid

2 波浪发电场配置储能系统

针对直驱式波浪能发电系统输出功率波动频率高的特点，本文选择超级电容器UC（ultra capacitor）储能平滑波浪发电系统输出功率的波动。UC 与普通电解电容在电气性能和物理尺寸方面有很大的差异。一个1 ～10 F 的UC 物理尺寸约等同于10 μF 的普通电解电容。UC 可看作是一个可充放电电池，其响应速度快，循环寿命长，可频繁充放电。

UC 储能系统主电路如图3 所示，UC 通过双向DC/DC 变换器和直流母线相连构成储能系统ESS（energy storage system），ESS 通过电压源型变流器与电力系统连接，对变流器和变换器进行控制，可以实现储能系统与电网之间功率的实时交换[7]。

图3 UC 储能系统主电路Fig.3 Main circuit of UC ESS

在波浪发电场中，储能系统可以装设在3 个地点：波浪发电系统背靠背变换器直流侧、波浪发电系统背靠背变换器的输出端和整个波电场的并网出口母线。将储能系统集中配置在波电场出口时，储能系统独立，便于维护和管理，因此，本文主要讨论第3 种方案。波电场配置ESS 如图4 所示。

波浪发电场配置ESS 后，波电场总输出功率是波浪发电系统总输出功率和储能系统输出功率之和，即

图4 波电场配置ESSFig.4 Wave farm installed ESS

式中：Poutput为波电场总输出功率；Pwave为波浪发电系统总输出功率；Pess为储能系统输出功率，当Pess为正时电池放电，为负时电池充电。

储能系统的输出功率起到平滑波机总输出功率的作用，即ESS 根据所设置的控制策略快速充放电，降低波电场总输出功率的波动，减小波浪发电并网对电网产生的影响。

3 输出功率平滑控制策略

一阶低通滤波器可以滤除信号中的高频分量，得到比较平滑的曲线[8]。本文将低通滤波原理应用于波电输出功率的平滑，另外，还提出了基于波电功率预测的功率平滑方法。

3.1 基于低通滤波原理的功率平滑策略

波电场总输出功率Poutput的值由波浪发电系统总输出功率Pwave一阶低通滤波器得到，即

一阶低通滤波器的时域表达式为

式中：τ为滤波器的时间常数；X 为滤波器输入；Y为滤波器输出。

通常实测的功率数据是离散的点，可将式（6）离散化，设采样周期为Δt，离散化得

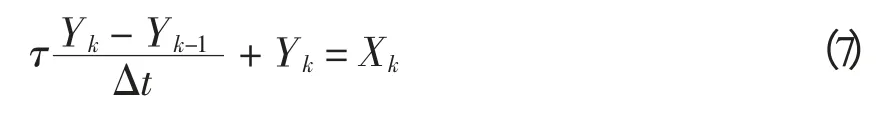
解得

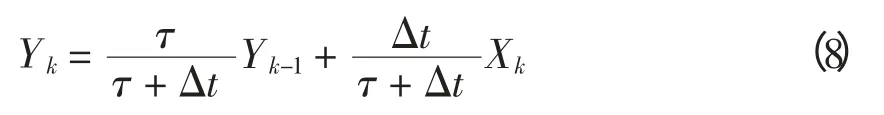
令a=τ/（τ+Δt），则式（8）可描述为

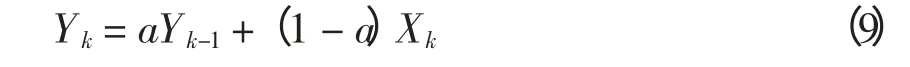
式中：Yk，Xk分别为tk=t0+kΔt 时刻波电场总输出功率Poutput，k和波浪发电系统总输出功率Pwave，k。则tk时刻储能系统输出功率为

3.2 基于波电功率预测技术的功率平滑策略

基于波电输出功率预测可获取输出功率变动趋势及变动范围，合理确定输出功率并网值。时间序列法就是通过大量的历史数据来建立预测模型，对未来某个时刻或某段时间的输出进行预测，具体的计算方法见文献[10]。通过采样可获取大量历史波电输出功率数据，对其进行时间序列分析，预测波电输出功率，确定波电场输出功率并网值。

设预测尺度为时间T，一次预测出n 个功率点，T 的取值可通过对历史数据的分析选取，取约1 个功率波动周期。

若tk时刻预测出此后T 时间内的功率数据为P1，P2，P3，…，Pn，则tk时波电场总输出功率为

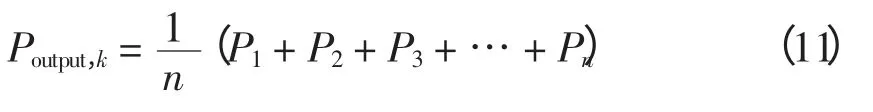
由于非规则波浪的波幅大幅度变化，为了进一步平滑输出的功率，必须对输出功率的变化率进行限制。定义波动率为

式中：ΔP 为输出功率的变化值，ΔP=Poutput，k-Poutput，k-1；PN为波浪发电系统装机容量。设置可接受的最大波动率γmax，从而得到可接受的最大功率波动量ΔP。

若Poutput，k＞Poutput，k-1+ΔP，说明波动超出所设置要求，令Poutput，k= Poutput，k-1+ ΔP；若Poutput，k＜Poutput，k-1-ΔP，说明波动超出所设置的要求，令Poutput，k=Poutput，k-1-ΔP；

在tk+1时刻，重新预测此后T 时间内功率，同理选取tk+1时刻的输出功率并网值，如此滚动确定每一时刻的输出并网功率值。

4 仿真分析

本文在Matlab/Simulink 仿真平台上搭建了AWS 直驱式波浪能发电系统并网模型[3]。为便于仿真分析，研究中采用一台波浪机发电系统对波浪发电场进行等效，其容量为1.5 MW。AWS 直驱式波浪能发电系统并网模型如图5 所示。

理想规则波浪作用下，波浪作用在浮子上的力Fwave如图6 所示，振荡周期为6 s。

波浪发电系统WECS（wave energy conversion system）的输出功率如图7 所示，采样周期为0.25 s。

运用低通滤波原理平滑的结果如图8 所示，τ为滤波时间常数。

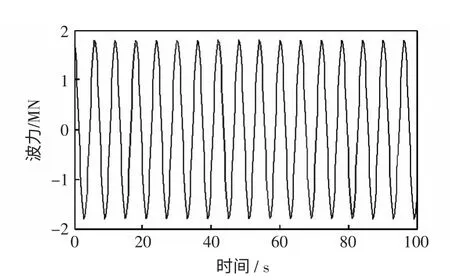
图6 理想波浪作用于AWS 浮子上的力Fig.6 Force acting on the AWS with ideal wave

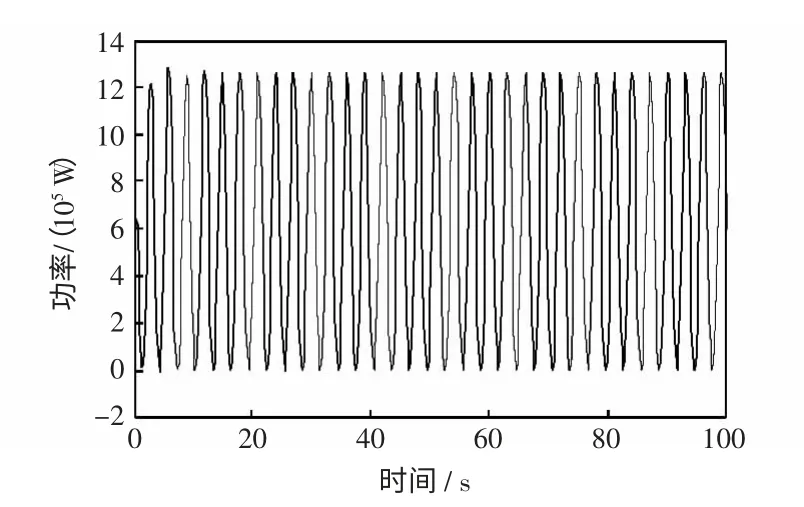
图7 理想波浪作用下的输出有功功率Fig.7 Output active power arting with ideal wave

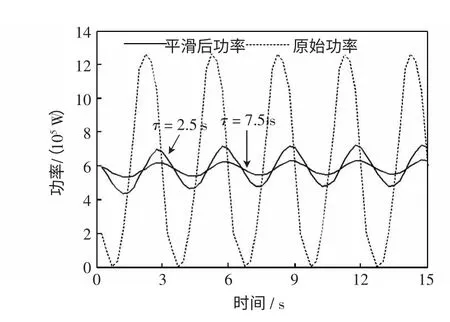
图8 低通滤波功率平滑效果Fig.8 Smoothing effect of power with low pass filter

运用功率预测方法平滑，为避免初始化过程的干扰，选取20～85 s 的260 个数据作为历史数据建立时间序列预测模型，85～100 s 的60 个数据作为待平滑数据。由历史数据可知其振荡周期为3 s，故预测尺度应选为3 s。由于采样数据是理想状态下的规则正弦波，并且通过Matlab 编程预测可知，预测模型能够准确进行3 s 预测，如图9 所示。平滑结果如图10 所示。

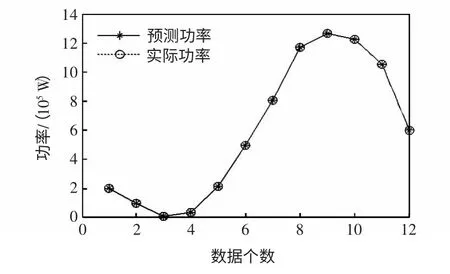
图9 预测功率与实际功率对比Fig.9 Comparison of the prediction power with real output power

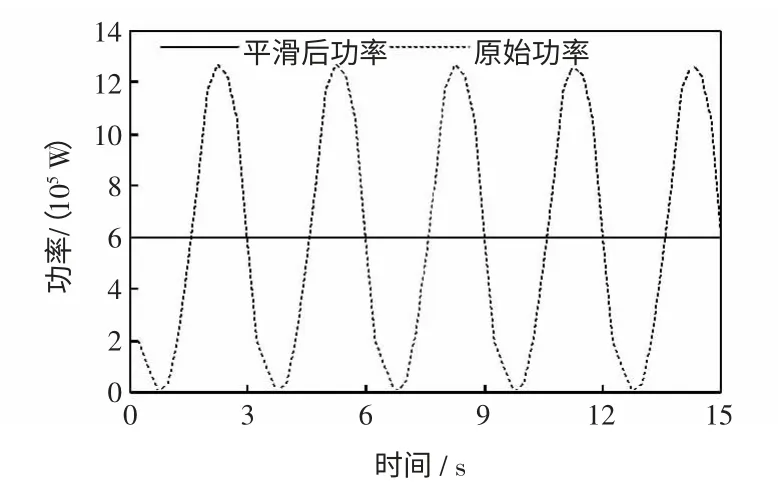
图10 功率预测法功率平滑效果Fig.10 Smoothing effect of power with power prediction method

可见，2 种方法都能有效平滑功率的波动。然而实际中波浪并不是理想状态的规则波浪，波浪作用在浮子上的力Fwave如图11 所示，采样周期与仿真时间同上。WECS 输出功率如图12 所示。

运用低通滤波法平滑的结果如图13 所示。

运用功率预测方法平滑，由历史数据可知振荡周期约为2.5 s，故预测尺度为2.5 s，通过Matlab编程仿真预测，2.5 s 预测结果如图14 所示。

由图14 可见，预测功率基本捕捉到实际功率的变化趋势及范围。

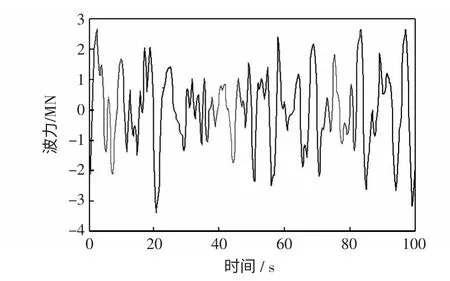
图11 非理想波浪作用于AWS 浮子上的力Fig.11 Force acting on the AWS with non-ideal wave

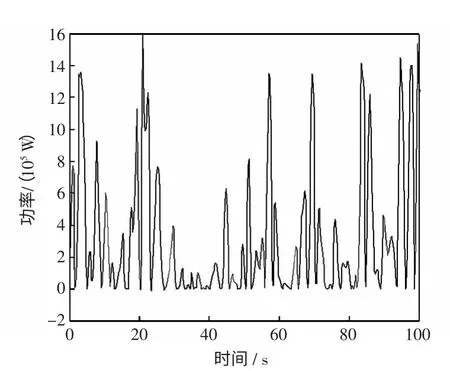
图12 非理想波浪作用下的输出有功功率Fig.12 Output active power arting with non-ideal wave

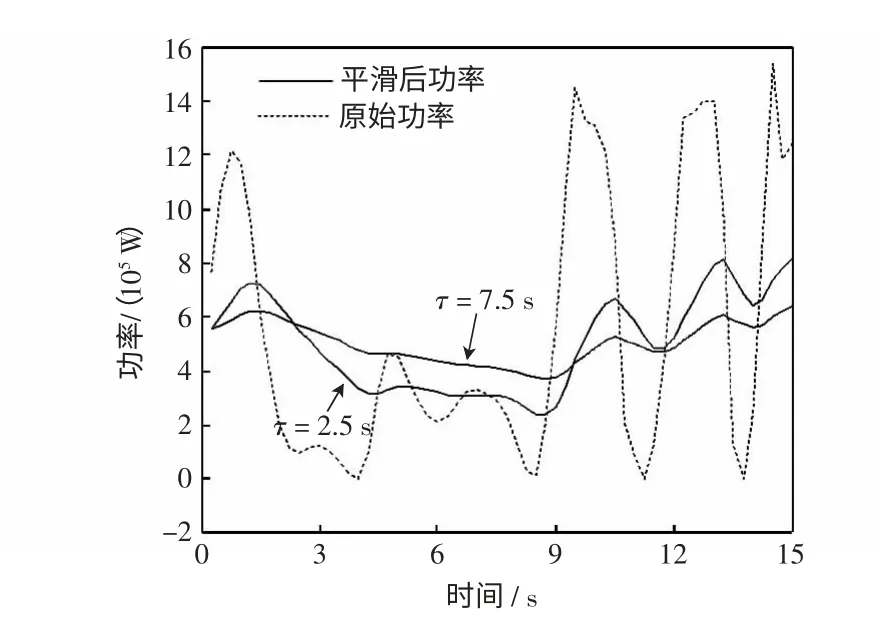
图13 低通滤波功率平滑效果Fig.13 Smoothing effect of power with low pass filter

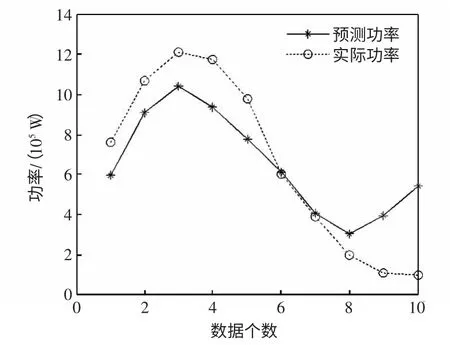
图14 预测功率与实际功率对比Fig.14 Comparison of the prediction power with real output power

设置可接受的最大波动率γmax分别为10%和2.5%，平滑结果如图15 所示。

由以上分析可见，2 种策略都能大大降低波浪发电场输出功率的波动，得到平滑的输出功率。2种平滑策略在不同参数下的相关结果如表1 和表2 所示。

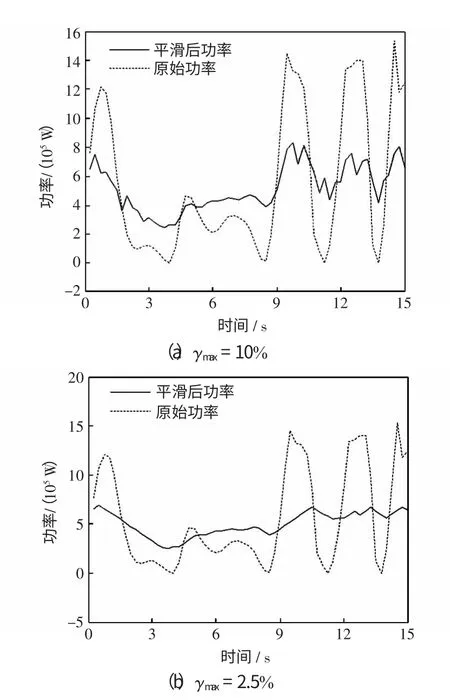
图15 设置不同最大波动率的功率平滑效果Fig.15 Smoothing effect of power when setting different γmax

表1 低通滤波法的结果Tab.1 Results of low pass filtering method

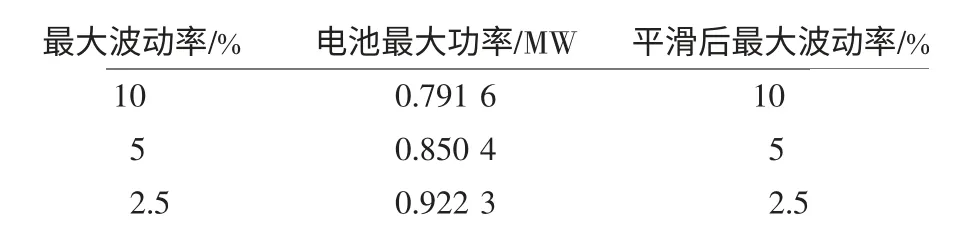
表2 功率预测法的平滑结果Tab.2 Results of output power prediction method

由表1 可知，时间常数越大，所需电池功率越大，输出功率越平滑。由表2 可知，设置可接受的最大波动率越小，所需电池功率越大，输出功率越平滑。当平滑后波动率在10%时，功率预测法电池最大功率为0.791 6 MW，而低通滤波法将大于0.821 9 MW；当平滑后波动率在5%时，功率预测法电池最大功率为0.850 4 MW，而低通滤波法将大于1.006 MW。即当平滑后最大波动率在同一水平时，功率预测法所需电池最大功率小于低通滤波法。同时，功率预测法是在平滑前设置最大波动率，而低通滤波法是平滑后才可得最大波动率，对于不同的功率数据，同样的时间常数平滑后的最大波动率可能不同。

5 结语

本文应用储能技术，提出2 种直驱式波浪能发电系统的输出功率平滑策略，一种基于低通滤波原理，另一种基于波电功率预测技术，克服了传统方法中平均功率难以获取的问题，通过动态仿真结果表明低通滤波法和功率预测法都能大大降低直驱式波浪能发电系统输出功率的波动。采用低通滤波法时，时间常数越大，输出功率越平滑，但电池最大充放电功率越大。采用功率预测法时，设置的最大波动率越小，所需电池最大充放电功率越大，输出功率越平滑。

[1]韩冰峰，褚金奎，熊叶胜，等（Han Bingfeng，Chu Jinkui，Xiong Yesheng，et al）.海洋波浪能发电研究进展（Progress of research on ocean wave energy power generation）[J].电网与清洁能源（Power System and Clean Energy），2012，28（2）：61-66.

[2]Brooking P R M，Mueller M A. Power conditioning of the output from a linear vernier hybrid permanent magnet generator for use in direct drive wave energy converters[J].IEE Proceedings-Generation，Transmission and Distribution，2005，152（5）：673-681.

[3]Wu Feng，Zhang Xiao-Ping，Ju Ping，et al. Modeling and control of AWS-based wave energy conversion integrated into power grid[J]. IEEE Trans on Power Systems，2008，23（3）：1196-1204.

[4]吴峰，张小平，鞠平（Wu Feng，Zhang Xiaoping，Ju Ping）.电池储能在直接驱动式波浪能发电场并网运行中的应用（Application of battery energy storage in the directdrive wave energy conversion farm integrated into power grid）[J].电力系统自动化（Automation of Electric Power Systems），2010，34（14）：31-36.

[5]Wu Feng，Zhang Xiao Ping，Ju Ping，et al. Optimal control for AWS-based wave energy conversion system [J]. IEEE Trans on Power Systems，2009，24（4）：1747-1755.

[6]Wu Feng，Ju Ping，Zhang Xiao-Ping，et al.Modeling，control strategy，and power conditioning for direct-drive wave energy conversion to operate with power grid [J].Proceedings of the IEEE，2013，101（4）：925-941.

[7]沈阳武，彭晓涛，杨军，等（Shen Yangwu，Peng Xiaotao，Yang Jun，et al）.超级电容器储能系统的功率实时控制（Real-time power control of ultracapacitor energy storage system）[J].电力自动化设备（Electric Power Automation Equipment），2011，31（11）：28-32，37.

[8]宇航（Yu Hang）.利用储能系统平抑风电功率波动的仿真研究（Simulation Research on Smoothing the Wind Power Fluctuation by Using Energy Storage System）[D].吉林：东北电力大学电气工程学院（Jilin：College of Electrical Engineering，Northeast Dianli University），2010.

[9]黄俊（Huang Jun）.配合风电接入的储能系统研究（The Study of Energy Storage System for the Grid-connected Wind Power System）[D].上海：上海交通大学电子信息与电气工程学院（Shanghai：School of Electronic Information and Electrical Engineering，Shanghai Jiaotong University），2012.

[10]孙劲松（Sun Jinsong）. 风电场输出功率预测的研究（Study on the Wind Power Forecasting of the Wind Farm）[D].保定：华北电力大学电气与电子工程学院（Baoding：School of Electrical and Electronic Engineering，North China Electric Power University），2009.

[11]吴雨，潘文霞，冯蒙霜，等（Wu Yu，Pan Wenxia，Feng Mengshuang，et al）. 基于混合储能的微电网功率控制策略（Power control strategy for microgrid based on hybrid energy storage system）[J]. 电力系统及其自动化学报（Proceedings of the CSU-EPSA），2013，25（2）：109-114，158.