风速分布模型在系统可靠性评估中的应用

李 慧

（北京信息科技大学自动化学院，北京100192）

风能是清洁的可再生能源，近年来，因其发电成本低廉和技术成熟已成为电力系统中相对增长较快的新能源。但与其他传统发电相比，风速具有随机性、波动性和间歇性，直接影响风电场的输出功率，导致风电并网后对电力系统的可靠性评估变得复杂。究其原因，主要存在两点：第一，风力发电机的输出功率取决于风速，而当前时刻的风速值是一个服从统计分布的随机量，风速预测的精度相对于负荷预测而言较低；第二，风机的输出功率与风速之间的关系是非线性的。因此，对于含有风电场的电力系统，需要建立正确的可靠性模型并分析其可靠性。

目前，国内外对含有风电场的电力系统可靠性评估研究较多。文献[1]建立了基于序贯蒙特卡罗方法的风电场发输电可靠性模型；文献[2]提出改进相关矩阵蒙特卡洛模拟法与拉丁超立方采样法相结合的多维相关风速抽样方法用于含有多个风电场的发输电系统可靠性评估；文献[3]考虑风速和负荷预测误差的随机性、风力发电机组和常规机组的停运率，应用分散抽样蒙特卡洛算法对含风电场的发电系统进行可靠性评估；文献[4]利用历史风速数据统计得到风机的出力概率分布图，并利用蒙特卡洛算法，对各种条件下风电并网后的电力系统进行可靠性评估；文献[5]考虑风电机组故障，将风电场可用容量的概率分布与可用风能的概率分布相结合，计算出风电场输出功率的概率分布，得到系统可靠性模型；文献[6]建立了多个风电场通用的风速概率分布模型，只需知道风电场的年平均风速和标准差就可以求解该风电场的概率分布；文献[7]在通用风速模型基础之上，综合考虑风机的输出功率特性以及风向的统计分布特性，建立了风电场的发电可靠性评估模型。然而，上述方法在进行风速建模时均是在加入其他约束或假设的前提下，用确定的数学函数拟合风速分布规律。实际上，风的不确定性无法用准确的数学函数来描述，尤其当出现双峰分布情况时，威布尔分布拟合效果较差[8-10]，从而导致系统可靠性评估的结果往往偏差较大。

最大熵原理在电力系统研究中已经得到了广泛应用，如风电功率预测[11]、电力系统故障选线[12]、状态估计及控制[13]等。文献[14-15]通过最大熵原理得到权重因数，对各种不同预测方法的结果进行加权，从而改进了风电预测的精度，本文思路与其类似，从风速的测量结果中得到约束条件，利用最大熵原理求解出满足约束条件的最大熵分布作为风速的真实分布。但是，相比以往使用的威布尔分布，本文提出的风速分布拟合方法未引入人为假设，从信息论的角度给出一种更为一般化的方法，从而能够更好地拟合各种环境下的风速分布。

本文运用最大熵原理，提出了一种新的风速分布建模方法用于风电系统可靠性评估。该方法采用历史风速数据的1 阶原点矩和2～4 阶中心矩拟合得到风速分布模型，并结合风机出力模型和传统机组出力模型的卷积结果来获得系统总的出力模型，通过计算充裕性指标来评价系统的可靠性。

1 基于最大熵原理的风电可靠性评估方法

1.1 基于最大熵原理的风速分布估计方法

最大熵原理由Jaynes 在1957年提出[16]：在对只掌握部分信息情况下的分布做出推断时，应该取符合约束条件但熵值最大的概率分布，这是唯一的不偏不倚的选择，任何其他的选择均添加了约束或假设。该原理成功地应用在光学图像复原、谱估计、综合负荷预测等领域。

1）最大熵原理求解的问题

某未知连续随机变量X，欲求其概率密度函数q（x）。已知其若干函数的期望为

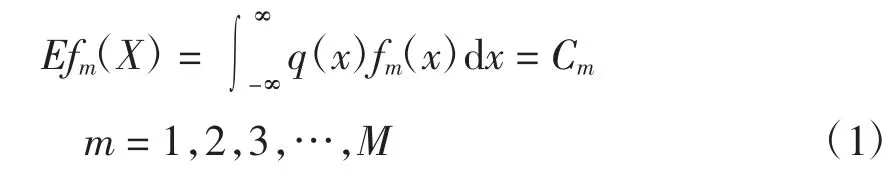
2）最大熵原理求解的思路

取微分熵最大为目标函数

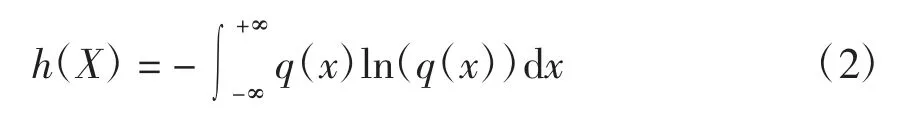
而概率密度函数必须满足

在式（1）和式（3）作为约束条件情况下，以微分熵最大为目标函数得到的最优解即为对于变量X 分布的最优推断。

3）最大熵原理求解的方法

引入拉格朗日Lagrange 乘子进行求解。取

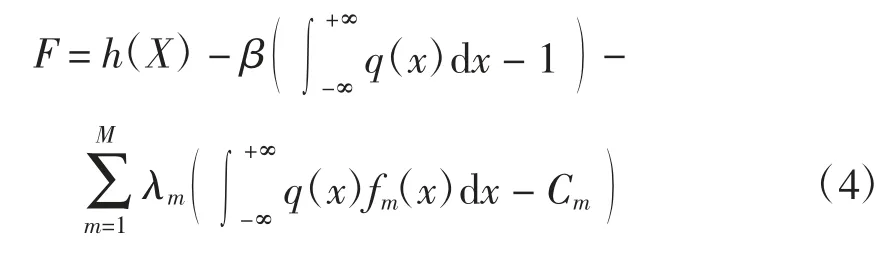
则

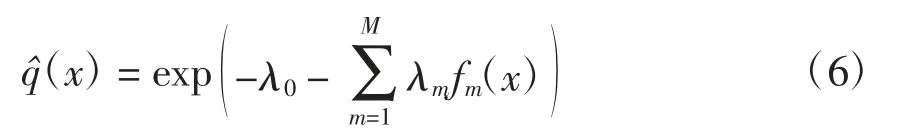
式中，λ0=β+1。将式（6）代入约束条件（1）和（3）中，便可解出各乘子λm（m=0，1，…，M）。

本文选取实测历史风速数据的1 阶原点矩、2～6 阶中心矩等统计量来描述风速的分布。原因是1 阶原点矩描述了风速的平均大小，2 阶中心矩体现了风速的方差，而3 阶以上中心矩反映了风速波形的情况。上述风速分布统计量可由原点矩和中心矩的定义获得，对应的部分表达式为

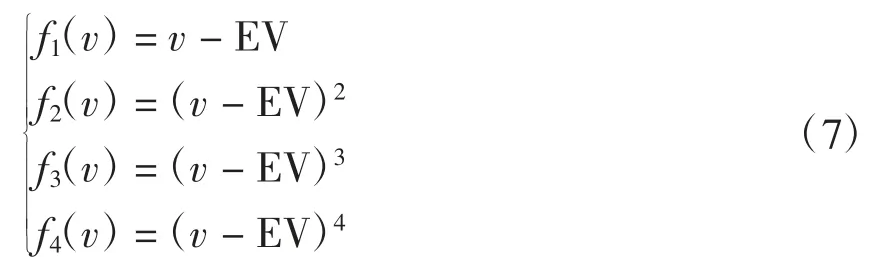
式中，EV 为风速的期望。

为了保证选取的约束条件能够较好地刻画风速分布，本文对风速统计量进行检验，确定中心矩的阶数。具体方法为：在同一地点随机抽取不同时间段的风速，分别计算2～6 阶中心矩，统计出各自的均值和标准差，将标准差与均值的比值作为检验指标，当比值小于给定的阈值（由试验所得）时，则判断该中心矩能反映风速的固有特征。然后，将式（6）、（7）代入式（1），便可求解出拉格朗日乘子，从而得到风速累计分布函数为

1.2 基于最大熵的风电可靠性评估建模与步骤

1.2.1 风机出力模型

风电机组的输出功率由风机本身参数与安装所在地风况共同决定。在确定风速模型之后，便可通过功率输出特性曲线[17]来表征风速与风机输出功率的关系，即风电机组输出特性。风电机组通常是在风速达到切入风速vci以上才开始工作，当风速达到额定风速vr以上时，即以额定功率值稳定输出，当风速高于切出风速vco时，则必须停机以保证风机的安全。所以，用分段函数来表达风速-功率特性最为合适。其中，在切入风速vci到额定风速vr这个区间内有多种关于功率特性的表达式，由文献[7]可知，采用二项式形式建立的风电机组输出功率模型较准确，本文取二项式形式作为风电机组输出功率表达式，即

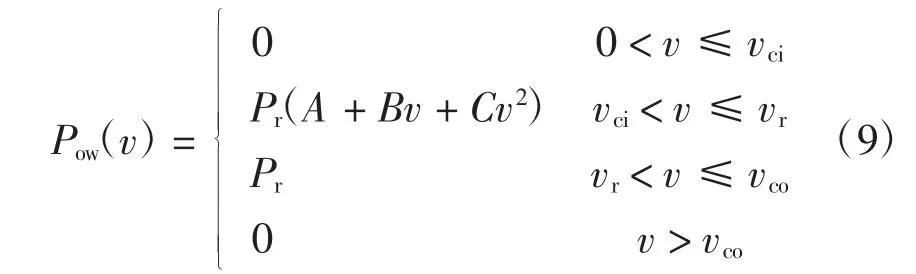
式中：Pr表示机组的额定功率；v 表示风速；A、B 和C 分别为风机功率特性曲线参数，其表达式为

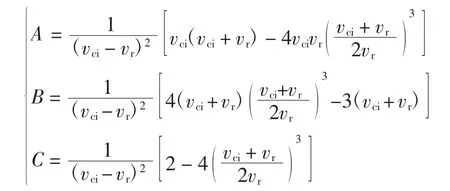
风电场通常是由许多处于同一地理位置、规格相同的风机单元组成，因此风机总出力可以通过将各台风机的风速对应出力相加得到。由于本文重点是考虑最大熵原理所拟合的风速分布效果，故假定所有风机的风速一致。由风速概率分布和风电机组输出特性可以得到风电机组输出功率的累积概率分布，如式（10）～式（12）所示。

（1）当0 ＜v ≤vci或v ＞vco时，Pow=0，则

（2）当vci＜v ≤vr时，0 ＜Pow≤Pr，则

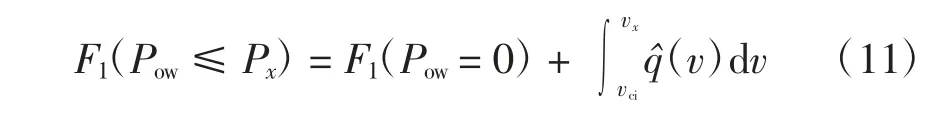
（3）当vr＜v ≤vco时，Pow=Pr，则

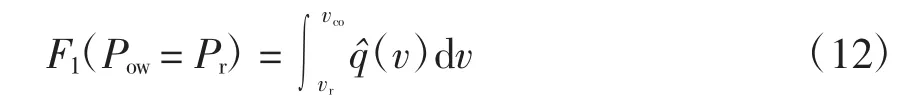
1.2.2 引入风机后的系统出力模型

文献[18]给出了由停运概率表所表示的传统发电机组的出力概率分布。可是，当引入风电机组后，系统的总出力等于风机发电和传统机组发电的总和，此时停运概率表的获取方法略有不同。本文采用通用生成函数法[19]，将风机的出力离散化，与传统机组出力的概率分布函数进行卷积，即可得到系统总出力的概率分布。方法是：先构造两个自变量为z 的函数，分别为U1（z）和U2（z），即

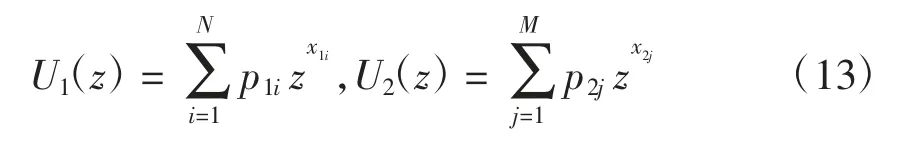
式中：x1i和x2j分别表示第i 台风机和第j 台传统机组的出力；p1i和p2j分别表示第i 台风机和第j 台传统机组对应的出力概率。于是，系统总的出力概率分布计算公式为

对式（14）的计算结果合并同类项，便得到系统总的出力概率分布，由此获得对应的停运概率表。

1.2.3 系统充裕度评估模型

为了验证基于最大熵原理的风速拟合方法能更好地用于对未来的系统可靠性进行评估，本文采用充裕性指标——失负荷概率LOLP（loss of load probability）为计算比较对象，其数学表达式为

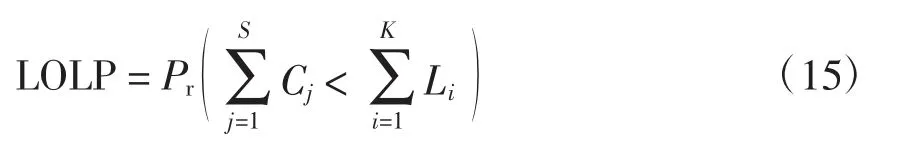
式中：Cj为发电机j 的发电能力；Li为负荷i 的大小。系统的LOLP 值表示给定时间范围内发电机出力小于负荷总量的状态全集的概率之和，它评价了系统发电能力的充裕性。

基于最大熵原理的风电系统可靠性评估计算流程如图1 所示。

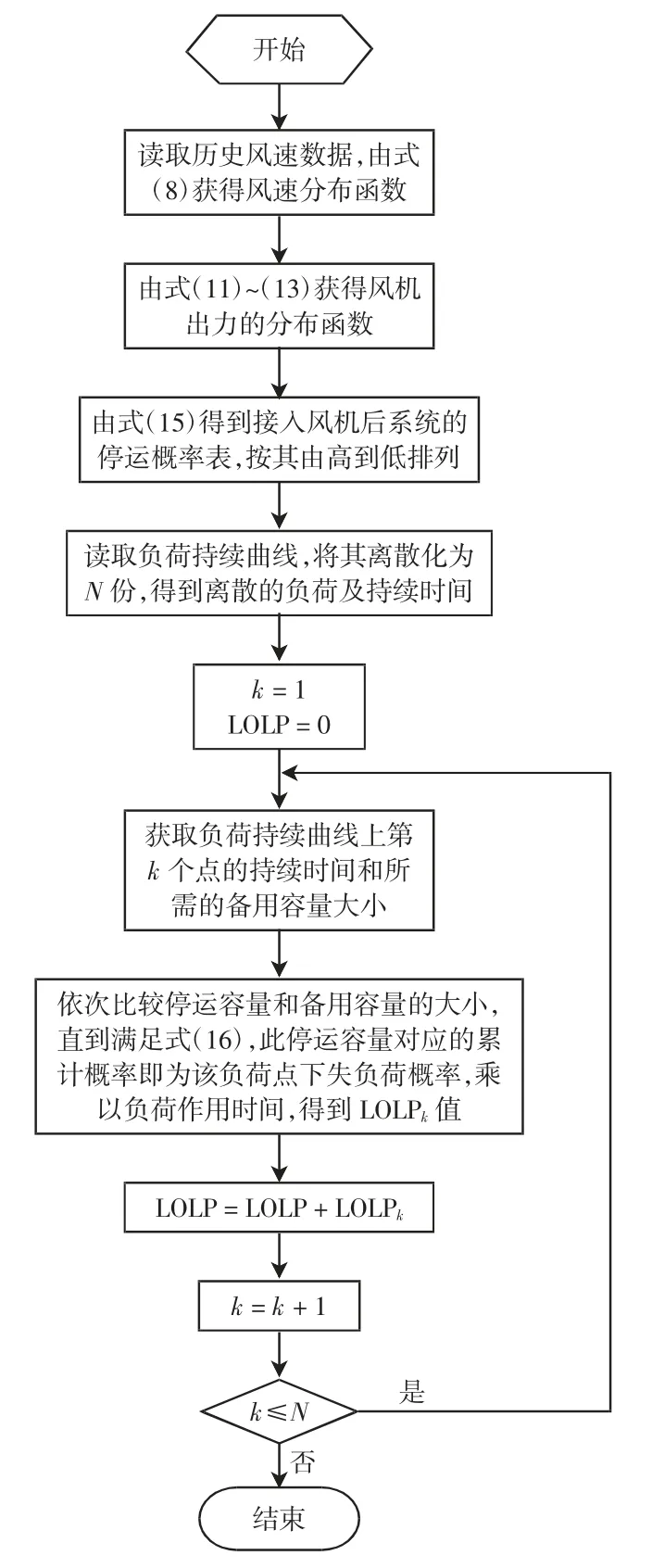
图1 基于最大熵原理的风电系统可靠性评估流程Fig.1 Flow chart of system reliability evaluation based on the maximum entropy principle

2 算例结果与分析

本文测试所用的风速数据来自美国国家可再生能源实验室NREL（national renewable energy laboratory）的西部风力资源数据集[20-22]，每10 min采集一个数据。本文将其2005年全年的风速数据作为样本集，用于拟合风速分布，将2006年全年的风速数据作为测试集，用于验证风速拟合方法在系统可靠性评估中的正确性和合理性。

2.1 风速分布建模及对比

将2005年全年的风速数据按照季节不同分成4 部分，分别对4 个季节和全年的风速统计量进行检验，如表1 所示。

以全年风速数据的检验为例，由表1 可以看出，2～4 阶中心矩的波动指标均小于7%，已满足代表风速固有特征的需求，所以选取2～4 阶中心矩即可，其对应的约束条件为

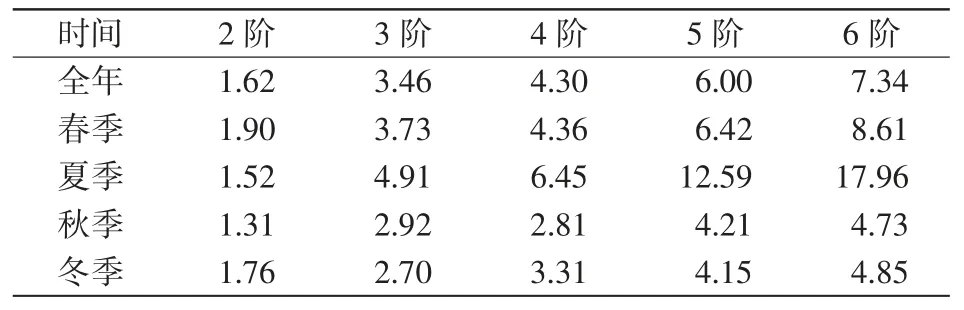
表1 风速统计量检验Tab.1 Test of the statistics %

按第1.1 节中所述方法求解出拉格朗日乘子，得到与之对应的风速概率密度函数为

采用最大熵原理与两参数威布尔分布2 种方法分别对2005年全年的风速数据进行拟合，其各自的风速概率密度函数如图2 所示。可以看出，当风速小于6 m/s 时，最大熵原理比威布尔分布更能逼近实际风速，真实地反映单峰情况下风速的分布特点。

图2 2005年全年2 种分布的风速概率密度函数Fig.2 Two probability density functions of wind speed in 2005

2.2 充裕性评估对比

本文用Matlab 编写程序，选择RBTS（roy billinton test system）为可靠性测试系统，其单线图如图3 所示。该系统包括2 个发电机节点（PV 节点）、4 个负荷节点（PQ 节点）、10 条传输线和11 个发电机组，发电机组的最小额定功率是5 MW，最大是40 MW，传输线的电压等级是230 kV，电压限制为1.05 p.u.和0.97 p.u.，系统的峰值负荷是185 MW，总装机容量是240 MW，系统元件的具体参数见文献[23]。

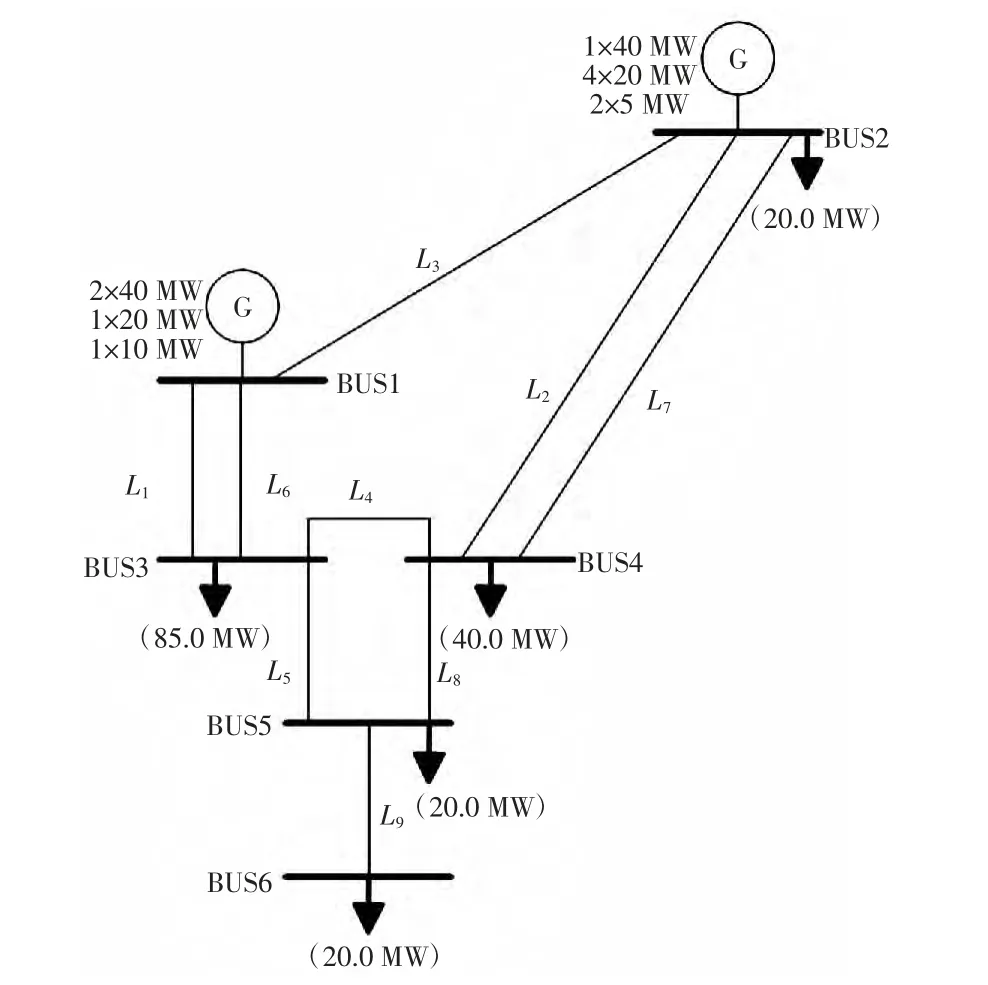
图3 RBTS 系统单线图Fig.3 Single line diagram of RBTS

为了验证最大熵分布适用于风电可靠性评估，考虑在原有测试系统上加入了20 MW 的风电机组，对应的风电渗透率为7.7%。由文献[24]可知，风机的强迫停运率对系统的可靠性指标影响非常小，故本文忽略风电机组故障率的影响。

表2 列出了采用最大熵原理和威布尔分布2种风速分布建模方法后预测得到的2006 全年和4个季节的系统充裕性评估指标LOLP 值（10-4）及其与实际值的偏差。图4 为2005年夏季两种分布的风速概率密度函数对比图。

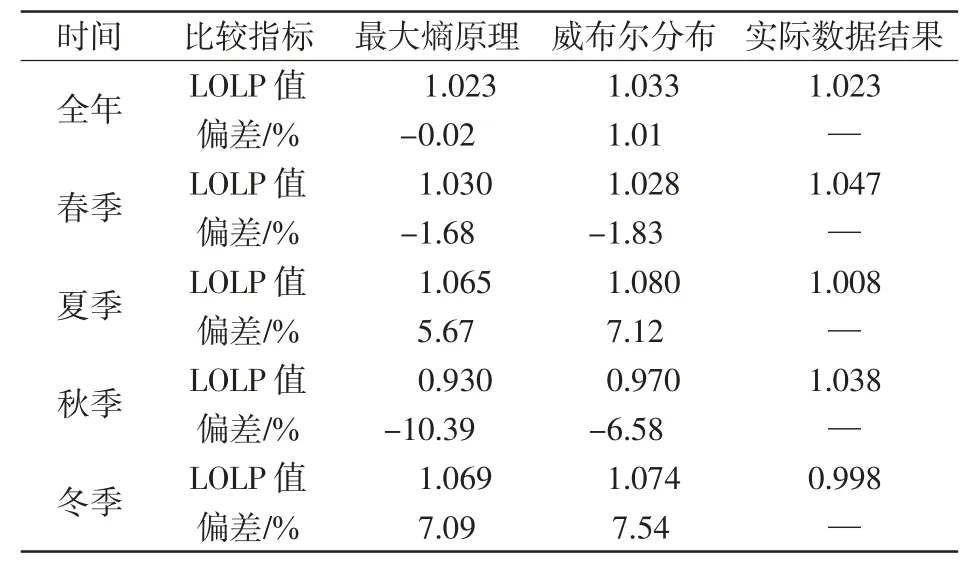
表2 两种风速拟合方法得到的可靠性指标Tab.2 Reliability index calculated by two fitting methods of wind speed

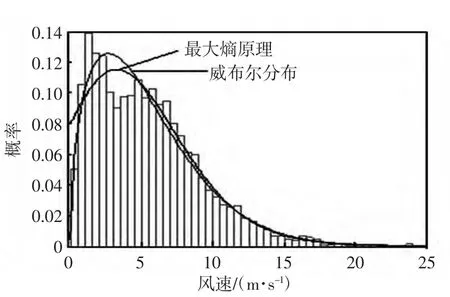
图4 2005年夏季两种分布的风速概率密度函数Fig.4 Two probability density functions of wind speed in the summer of 2005

由表2 可以看出，全年和春季情况下两种方法得到的LOLP 值与实际值都很接近，且最大熵原理得到的结果更优；而其他季节下二者的LOLP 值略偏离实际值（秋季更为严重），原因是没有考虑不同年份之间风速分布的变化。但是，总体来说，最大熵原理仍优于威布尔分布，以夏季为例，风速分布在2 m/s 和6 m/s 左右出现双峰的情况（见图4），比较二者的偏差指标分别为5.67%和7.12%，由此说明最大熵原理获得的风速分布更能反映实际情况。

3 结语

本文提出一种基于最大熵原理的风速分布模型用于风电场可靠性评估，以RBTS 测试系统为例，验证了方法的正确性和实用性。该方法不仅能对单峰情况的风速分布进行有效拟合，而且对多峰的风速分布也有较好地拟合效果，从而为含有风电场的电力系统可靠性评估提供了有利保障。

[1]姜文，严正，杨建林（Jiang Wen，Yan Zheng，Yang Jianlin）.计及风电场的发输电可靠性评估（Reliability assessment of composite generation and transmission system considering wind farms）[J].电力系统保护与控制（Power System Protection and Control），2010，38（22）：126-130，178.

[2]秦志龙，李文沅，熊小伏（Qin Zhilong，Li Wenyuan，Xiong Xiaofu）.含具有风速相关性风电场的发输电系统可靠性评估（Reliability assessment of composite generation and transmission systems with wind farms considering wind speed correlations）[J]. 电力系统保护与控制（Power System Protection and Control），2013，41（20）：27-33.

[3]蒋程，刘文霞，于雷，等（Jiang Cheng，Liu Wenxia，Yu Lei，et al）.计及风电的发电系统可靠性评估（Reliability assessment of power generation system considering wind power penetration）[J]. 电力系统及其自动化学报（Proceedings of the CSU-EPSA），2013，25（4）：7-13.

[4]余民，杨旻宸，蒋传文，等（Yu Min，Yang Minchen，Jiang Chuanwen，et al）.风电并网后电力系统可靠性评估和备用优化研究（Study on power system reliability and reserve optimization with wind power integration）[J].电力系统保护与控制（Power System Protection and Control），2012，40（12）：100-104，135.

[5]吴林伟，张建华，刘若溪（Wu Linwei，Zhang Jianhua，Liu Ruoxi）.考虑风电机组故障的风电场可靠性模型及其应用（A wind farm reliability model considering wind turbine faults and its application）[J].电力系统自动化（Automation of Electric Power Systems），2012，36（16）：31-35.

[6]Karki Rajesh，Hu Po，Billinton Roy. A simplified wind power generation model for reliability evaluation [J].IEEE Trans on Energy Conversion，2006，21（2）：533-540.

[7]汪海瑛，白晓民（Wang Haiying，Bai Xiaomin）.大规模风电场的发电充裕度与容量可信度评估（Assessment on generation adequacy and capacity credit for large-scale wind farm）[J]. 电网技术（Power System Technology），2012，36（6）：200-206.

[8]Kececioglu D B，Wendai Wang. Parameter estimation for mixed-Weibull distribution[C]//Annual Reliability and Maintainability Symposium.Anaheim，USA：1998.

[9]江岳文，陈冲，温步瀛（Jiang Yuewen，Chen Chong，Wen Buying）.含风电场的电力系统机组组合问题随机模拟粒子群算法（Particle swarm research of stochastic simulation for unit commitment in wind farms integrated power system）[J].电工技术学报（Transactions of China Electrotechnical Society），2009，24（6）：129-137.

[10]王松岩，于继来，李海峰，等（Wang Songyan，Yu Jilai，Li Haifeng，et al）.考虑统计和互相关特性的多风电场风速数据模拟生成方法（A wind speed modeling method for multiple wind farms considering correlation and statistical characteristics）[J].电力系统自动化（Automation of Electric Power Systems），2013，37（6）：18-23，83.

[11]夏冬，吴俊勇，贺电，等（Xia Dong，Wu Junyong，He Dian，et al）.一种新型的风电功率预测综合模型（A novel combined model for wind power forecasting based on maximum entropy principle）[J].电工技术学报（Transactions ofChinaElectrotechnicalSociety），2011，26（S1）：262-266.

[12]贾清泉，石磊磊，王宁，等（Jia Qingquan，Shi Leilei，Wang Ning，et al）.基于证据理论和信息熵的消弧线圈接地电网融合选线方法（A fusion method for ground fault line detection in compensated power networks based on evidence theory and information entropy）[J].电工技术学报（Transactions of China Electrotechnical Society），2012，27（6）：191-197.

[13]杨卫东（Yang Weidong）.熵原理在电力系统中的应用前景（Application prospects of entropy theory in power systems）[J]. 电力建设（Electric Power Construction），2000，21（3）：17-19，30.

[14]Han Shuang，Liu Yongqian，Li Jinshan. Wind power combination prediction based on the maximum information entropy principle[C]//World Automation Congress Proceedings.Puerto Vallarta，Mexico：2012.

[15]Han Shuang，Liu Yongqian.The study of wind power combination prediction[C]//Asia-Pacific Power and Energy Engineering Conference.Chengdu，China：2010.

[16]Jaynes E T. Information theory and statistical mechanics[J].Physical Review，1957，106（4）：620-630.

[17]An Jing，Yang Jingyan. Reliability evaluation for distribution system considering the correlation of wind turbines[C]//International Conference on Advanced Power System Automation and Protection.Beijing，China：2011.

[18]郭永基.电力系统可靠性分析[M].北京：清华大学出版社，2003.

[19]Lisnianki A，Frenkel I，Ding Y.Multi-state System Reliability Analysis and Optimization for Engineers and Industrial Managers[M].London：Springer，2010.

[20]Lew D，Milligan M，Jordan G，et al.How do wind and solar power affect grid operations：The western wind and solar integration study[C]//8th International Workshop on Large Scale Integration of Wind Power and on Transmission Networks for Offshore Wind Farms.Bremen，Germany：2009.

[21]Potter C W，Lew D，McCaa J，et al.Creating the dataset for the western wind and solar integration study[J]. Wind Engineering，2008，32（4）：325-338.

[22]US Department of Energy，National Renewable Energy Laboratory. Western wind resource metadata file [EB/OL].http：//wind.nrel.gov/Web_nrel，2013.

[23]Billinton R，Kumar S，Chowdhury N，et al.A reliability test system for educational purposes-basic data[J].IEEE Trans on Power Systems，1989，4（3）：1238-1244.

[24]Billinton R，Yi Gao. Multistate wind energy conversion system models for adequacy assessment of generating systems incorporating wind energy[J]. IEEE Trans on Energy Conversion，2008，23（1）：163-170.