二元上尾独立随机变量和的精确大偏差

(铁岭市师范高等专科学校，辽宁铁岭112001)

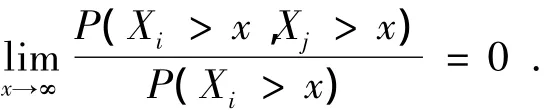
设{ηn，n≥1}为一服从二元上尾独立分布的随机变量序列，其共同分布为A(x)=P(η≤x).设{Nt，t≥0}为一个与{ηn，n≥1}独立的取非负整数值的计数过程.记为确定和，非确定和，它们的尾概率的性态可以用来评估保险公司的破产概率，而重尾分布可以刻画这种特性，所以近年来学者们特别关注重尾随机变量和的精确大偏差的极限性态.文献［5］研究了独立同分布带有长尾的随机变量和的精确大偏差，文献［6］研究了负相依关系的带有长尾分布的随机变量和的精确大偏差.文献［4］中提出二元上尾独立的概念，本文在此基础上讨论了长尾分布上的二元上尾独立关系的随机变量和的精确大偏差.

1 确定和的精确大偏差

以下采用记号a1(x)＞a2(x)，如果limx→∞inf，其中a(·)和a(·)是两个取正值的12函数.

定理2.1 设{ηn，n≥1}为一个二元上尾独立的随机变量序列，其共同分布为服从长尾分布的分布函数A(x)，且存在有限的数学期望μ，则对任意常数a＞0，当n→∞ 时，对x≥an一致地有:

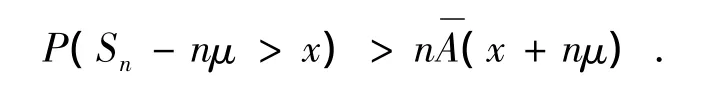
2 非确定和的精确大偏差

由文献［1］我们给出一个假设条件:

当t→∞ 时，对于任意的δ＞0和任意小的有

［1］ Ng.K.W，Tang.Q，Yan.J.A，et.al.Precise large deviation for sums of random variables with consistently varying tails［J］.J.Appl.Prob，2004，41:93-107.

［2］ Tang，Q.Insensitivity to negative dependence of the asymptotic behavior of precise large deviations［J］.Electron.J.Probab.2006，11:107-120.

［3］ Chen，Y.，Zhang，W.(2007).Large deviations for random sums of negatively dependent random variables with heavy or subexponential tails［J］.Statist.Probab.Lett.77:530-538.

［4］ Zhang Yi，Shen Xinmei，Weng Chengguo.Approximation of the tail probability of randomly weighted sums and applications［J］.Stochastic Processes and their applications，2009，119:655-675.

［5］ F.Loukissas.Precise large deviations for long-tailed distributions［J］.Theoretical Probability，2012，25(4):913-924.

［6］ D.Konstantinides，F.Loukissas.Precise large deviations for Sums of Negatively Dependent Random Variables with Common Long-Tailed Distributions［J］.Statistics-Theory and Methods.2011，40:3663-3671.