复合材料面层－泡沫金属夹芯板的振动及吸能特性分析

何柏灵，赵桂平，卢天健

(西安交通大学 机械结构强度与振动国家重点实验室，陕西 西安710049)

0 引言

复合材料夹芯结构的面层通常由高密度、高刚度的各向异性薄板组成，芯体则由刚度和密度都较低的泡沫材料构成。面层承受切向载荷和弯矩，芯体承受横向剪切和垂直载荷。随着复合材料夹芯结构在超音速/高超音速飞行器和舰船中的大量应用，其在冲击载荷作用下的振动问题日益受到关注。

泡沫夹芯结构振动特性研究方法的不同，主要体现在如何考虑芯层的受力状态及变形模式。针对泡沫夹芯结构在外载荷作用下弹性变形阶段的动态响应，Hause 等［1-2］、Librescu 等［3-4］认为泡沫芯层的厚度远大于面层厚度，前者受到冲击载荷作用时的横向压缩变形相对其厚度可忽略不计，因此在分析时忽略了芯层的横向可压缩性，认为上下面层和芯层的横向位移一致，但依然考虑芯层的横向剪切变形。与此相反，Frostig 等［5］、Radford 等［6］、Tagarielli等［7］认为当夹芯结构受到冲击载荷作用时，泡沫芯层沿厚度方向有不可忽略的横向压缩和剪切变形，必须考虑芯层的横向压缩和剪切特性。Frostig 等［5］对面层使用了Kirchhoff 理论，对芯层则考虑了横向压缩和剪切特性，引入芯层的横向剪切应力作为未知变量，利用混合应力-位移模型表示芯层的位移场，进而讨论了弹性变形时泡沫夹芯结构的静态响应。Radford 等［6］、Tagarielli 等［7］则通过实验表明:泡沫夹芯结构在受到冲击载荷时，沿厚度方向发生了不可忽略的横向压缩和剪切变形。

鉴于此，本文认为泡沫金属夹芯结构的芯层在受到冲击载荷作用时，其横向正应变和剪切应变不能忽略。并且，提出了一个考虑芯层横向压缩和剪切特性的高阶模型，重点分析弹性变形时泡沫夹芯结构的振动响应及能量吸收特性。

1 问题描述与基本方程

由于应用在舰船或飞机副翼上的夹芯结构沿舰身或翼展方向的几何尺寸远大于其厚度，为简化分析，将其等效为平面应变问题处理，如图1所示。

图1 泡沫金属夹芯板Fig.1 Sandwich plate with metal foam core

在模型中，tf为面层厚度，tc为芯层厚度。在高阶模型中，采用与厚度方向有关的2 级幂级数描述芯层沿x 方向的位移(图1)，采用与厚度方向有关的1 级幂级数描述芯层沿z 方向的位移。同时，模型满足芯层和面层交界处位移连续条件。

模型基本假设:

1)复合材料面层很薄，刚度很大，承受切向载荷和弯矩，遵循Kirchhoff 假设;

2)泡沫金属芯层刚度较弱，承受横向正应力和剪切应力，具有横向压缩和剪切特性;

3)不考虑泡沫金属夹芯结构的缺陷，认为面层和芯层理想粘接。

上面层的位移场表示为

式中:v1t、v3t分别为上面层在x 方向、z 方向位移;u1t、分别为上面层中线在x 方向、z 方向位移。

下面层的位移场表示为

式中:v1b、v3b分别为下面层在x 方向、z 方向位移;u1b、u3b分别为下面层中线在x 方向、z 方向位移。

由于中间芯层的变形十分复杂，故引入非线性高阶位移场［8］，表示为

式中:v1c、v3c分别为芯层在x 方向、z 方向位移;Φ1c为芯层的形变程度，是引入的挠曲函数;

动能变分δT 可写成

应变能变分δU 可写为

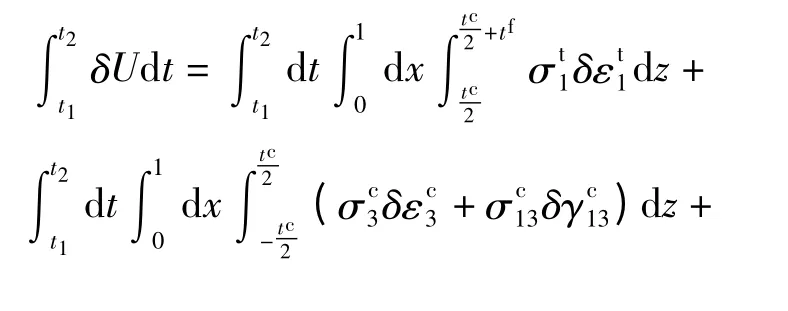
由于遵循Kirchhoff 假设，上、下面层沿z 方向的应变为0，只考虑其沿x 方向的应变能;由于中间芯层在z 方向发生压缩和剪切变形，其在z 方向的应变能远远大于x 方向的应变能，中间芯层沿x 方向的应变能忽略不计。

虚功变分δW 可写成

式中:q3t为作用于上面层的外力。

将(4)式～(6)式代入哈密尔顿方程，得到与位移变分δu1a，δu1d，δu3a，δu3d，δφ1c相关的控制方程分别为:

由方程(11)式求得

将其代入方程(10)式得到

2 方程求解

对位移u1a、u1d、u3a、u3d进行变量分离。令=式中:Ns 为振型阶数。

将变量分离的位移表达式代入方程(7)式～(9)式和(12)式，利用加权伽辽金方法进行简化，得到夹芯结构的振动方程:

求解方程(13)式时引入边界条件:

初始条件:ua1(x，0)= ud1(x，0)= ua3(x，0)=0)=0.

为了满足边界条件，则{φa11(x)，φa12(x)，…，式中:Wi(x)为两端固支的欧拉-伯努利梁的第i 阶正则化振型，定义为式 中:(x)=cosh βix)，βi为cos βcosh β -1 =0 第i 阶根，βi=(i+0.5)π ，i=1，2，…，Ns.

假设冲击载荷作用在夹芯结构上可近似为均匀分布，表达式［9］为

当r=1 时，冲击载荷变为三角激励。令冲击波作用时间tp=0.001 s，压力p0=200 kPa.

根据给定边界条件和初始条件，利用4 阶Runge-Kutta 法求解振动方程(13)式后利用振型叠加求得整个夹芯结构的位移场。

3 结果与分析

由于现有文献中很难找到复合材料夹芯板平面应变问题的动态响应研究结果，所以为了验证本文的理论模型，计算了夹芯板的固有频率，并与文献［10］的结果进行了比较，如表1所示。

表1中同时给出了经典层合板理论和有限元软件ABAQUS 的数值计算结果。在数值计算中，使用2 次高阶平面应变单元CPE6MH 剖分芯体网格，使用线性平面应变单元CPE3H 剖分面层网格，结构采用两端固支边界条件。可看出，本文计算的夹芯板固有频率与文献［10］和ABAQUS 计算的结果非常接近。而经典层合板理论的计算结果远远大于其他三者，因为经典层合板理论忽略了芯体的横向可压缩性和剪切变形。由此可看出，高阶理论能准确预测泡沫金属夹芯板的模态，进而表明了高阶理论计算泡沫金属夹芯板振动响应的可行性。

表1 夹芯板的前4 阶固有频率Tab.1 The first fourth-order inherent frequency of the sandwich plate

假设H =2tf+tc，夹芯结构的面层由纤维增强复合材料层合板组成，铺层顺序为［3θ/2θ/θ/芯层厚度/θ/2θ/3θ］，芯层由闭孔铝泡沫组成。

面层材料参数［11］为:=131 GPa，=10.344 GPa，ν13=0.22，ρf=1 627 kg/m3，tf=1 mm;夹芯层材料参数为［12］:Ec=1 GPa，νc=0.3，ρc=250 kg/m3，tc=20 mm.取Ns=8，即采用8 阶振型叠加。

夹芯板的质量比例阻尼c 表示［13］为c=εw1，其中w1=1 230 Hz 为夹芯板基频。

在三角激励作用下，应用本文的高阶理论给出了反映不同面层铺设角、不同阻尼比及不同芯层厚度的泡沫铝夹芯板中点挠度的值如图2～图4所示。

图2 面层不同铺设角度的泡沫夹芯板的振动响应Fig.2 Vibration responses of sandwich plates with foam cores at different laying angles

由图2可看出，复合材料面层铺设角度对夹芯板中点挠度的影响十分显著。在芯层材料和厚度不变的情况下，夹芯板的整体刚度随面层纤维铺设方向的不同而改变。当纤维铺设角度θ =0°时，夹芯板中点挠度最小。

由图3可看出，在冲击载荷作用下，泡沫铝夹芯板的阻尼系数越大，其能量耗散越快，即振幅衰减越快。

由图4可看出，泡沫铝芯层越薄，板的振动响应振幅越大，夹芯板越容易破环。

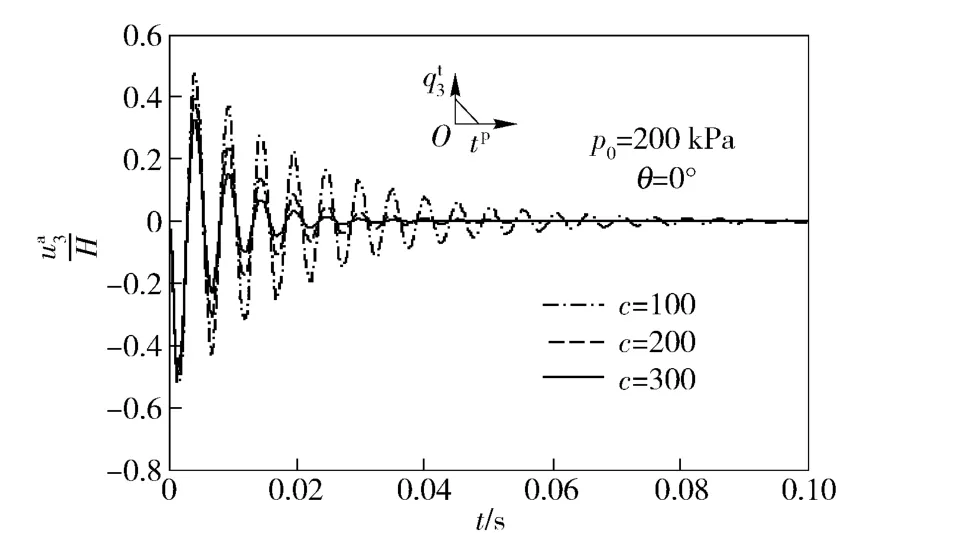
图3 不同阻尼系数的泡沫夹芯板振动响应Fig.3 Vibration responses of sandwich plates with foam cores with different damping coefficients

图4 不同芯层厚度的泡沫夹芯板振动响应Fig.4 Vibration response of the sandwich plate with foam core at different core thickness

在三角激励的脉冲载荷作用下，采用考虑芯层横向压缩和剪切变形的高阶夹芯板理论，讨论泡沫铝夹芯板的能量吸收行为。

如图5和图6所示泡沫铝夹芯板的面层和芯层各部位在外载荷作用下不同时刻的能量密度变化。

可看出:芯层由于具有横向压缩和剪切变形，具有承受横向正应力和剪切应力的能力，从而可吸收大量能量;由于芯层具有横向压缩和剪切变形，在z方向发生压缩和剪切变形，与z 方向有关的应变能远远大于x 方向的应变能，故分析时可仅考虑前者。

图5 t=0.001 9 s 时面层和芯层的应变能密度Fig.5 Deformation strain desities of facesheet and core at t=0.001 9 s

图6 t=0.006 2 s 时面层和芯层的应变能密度Fig.6 Deformation strain desities of facesheet and core at t=0.006 2 s

根据芯层应变能密度U2可得:结构两端固支，芯层两端不吸能。对于面层而言，因为其遵循Kirchhoff 理论，z 方向应变为0，可只考虑x 方向的应变能。根据面层应变能密度U1可得:结构两端固支，面层两端吸能。

4 结论

本文针对泡沫夹芯结构在超音速/高超音速飞行器和舰船中的应用背景，通过高阶理论，对泡沫金属夹芯结构在冲击载荷作用下的振动及吸能特性进行分析，利用加权伽辽金方法和4 阶Runge-Kutta 法求解控制方程，得到问题的数值解。并且将理论预测的夹芯结构振动模态和文献［10］的计算结果进行比较，说明高阶理论在求解泡沫夹芯结构振动响应问题上的可行性。

对于复合材料面层填充泡沫金属芯体的夹芯结构，改变其材料参数及复合材料面层铺层角度，通过计算夹芯结构的动态位移ua3，可以得出以下结论:

1)面层铺层角度会改变泡沫金属夹芯结构的整体刚度，进而对挠度产生影响:θ =0°，15°，30°三种铺层角度中，θ =0°时泡沫夹芯板挠度最小、铺层角度最佳。

2)阻尼系数越大，能量耗散越快，泡沫夹芯板的振幅衰减越快。

3)芯层越厚，泡沫夹芯板的振幅越小，发生变形破坏概率越小。

4)芯层由于具有横向压缩和剪切变形特性，可承受横向正应力和剪切应力，在动载响应中具有良好的吸能特性。

本文基于弹性假设提出的模型具有一定的局限性。当泡沫夹芯在冲击载荷下产生明显的塑性变形时，本文方法不再适用。

References)

［1］ Hause T，Librescu L.Dynamic response of anisotropic sandwich flat panels to explosive pressure pulses［J］.International Journal of Impact Engineering，2005，31(5):607 -628.

［2］ Hause T，Librescu L.Dynamic response of doubly-curved anisotropic sandwich panels impacted by blast loadings［J］.International Journal of Solids and Structures，2007，44(20):6678 -6700.

［3］ Librescu L，Oh S Y，Hohe J.Linear and non-linear dynamic response of sandwich panels to blast loading［J］.Composites Part B:Engineering，2004，35(6):673 -683.

［4］ Librescu L，Oh S Y，Hohe J.Dynamic response of anisotropic sandwich flat panels to underwater and in-air explosions［J］.International Journal of Solids and Structures，2006，43(13):3794 -3816.

［5］ Frostig Y，Baruch M，Vilnay O，et al.High-order theory for sandwich-beam behavior with transversely flexible core［J］.Journal of Engineering Mechanics，1992，118(5):1026 -1043.

［6］ Radford D D，McShane G J，Deshpande V S，et al.The response of clamped sandwich plates with metallic foam cores to simulated blast loading［J］.International Journal of Solids and Structures，2006，43(7):2243 -2259.

［7］ Tagarielli V L，Deshpande V S，Fleck N A.Prediction of the dynamic response of composite sandwich beams under shock loading［J］.International Journal of Impact Engineering，2010，37(7):854 -864.

［8］ 冯一哲，赵桂平，卢天健.软夹芯复合材料层合板的模态耦合研究［C］∥中国力学大会论文摘要集.哈尔滨:哈尔滨工业大学出版社，2011:138.FENG Yi-zhe，ZHAO Gui-ping，LU Tian-jian.Research on the mode coupling of composite sandwich plate with soft core［C］.Abstract Book Written by Chinese Academy Conference of Theoretical and Applied Mechanics.Harbin:Harbin Institute of Technology Press，2011:138.(in Chinese)

［9］ Librescu L，Nosier A.Response of shear deformable elastic laminated composite panels to sonic boom and explosive blast loadings［J］.AIAA Journal，1990，28(2):345 -352.

［10］ Qin Z，Batra R C.Local slamming impact of sandwich composite hulls［J］.International Journal of Solids and Structures，2009，46(10):2011 -2035.

［11］ Biglari H，Jafari A A.High-order free vibrations of doublycurved sandwich panels with flexible core based on a refined three-layered theory［J］.Composite Structures，2010，92(11):2685 -2694.

［12］ Radford D D，Fleck N A，Deshpande V S.The response of clamped sandwich beams subjected to shock loading［J］.International Journal of Impact Engineering，2006，32(6):968 -987.

［13］ Dogan V.Dynamic multimode response of composite plates to sonic boom and blast loadings［J］.Journal of Aircraft，2008，45(2):498 -507.