军用电站电缆雷电感应过电压影响因素研究

解璞，赵锦成，王川川，王勇

(军械工程学院 电子工程系，河北 石家庄050003)

0 引言

军用电站和负载舱体之间通过电缆连接，连接电缆一般为输电和控制电缆。对于军用电站，由于具有移动性特点，电缆贴地铺设，采用普通多芯橡胶绝缘电缆，多数电缆间没有作屏蔽均压处理，少数有屏蔽的电缆两端也没接地，造成电位不同，产生传输干扰，感应过电压侵入是造成野外军用电站供电系统损坏的主要途径之一。在整个电力系统工作的任意瞬间，雷电电磁脉冲有可能与系统中的地面电缆、信号线等多导体传输线耦合，在线路上感应出的电压和电流会沿着信号或电源通道传播到终端的控制设备和用电装备中，使装备受到损坏或发生工作失效，危及系统的安全可靠运行。因此亟待开展军用电站电缆雷电感应过电压影响因素研究。

1 雷云对地放电雷电电磁场计算

电缆感应过电压的计算主要分为两个部分:首先计算出雷云对地放电过程产生的雷电电磁场，然后根据场路耦合模型做进一步的分析，计算出其感应电压和电流。

计算雷电流产生的电磁场时，雷电回击电磁场的计算示意图如图1所示［1-2］。假设雷电回击放电通道近似为垂直于地面的长为h 的竖直天线，回击电路以匀速v 从地面沿通道向上传输，电流和电荷在通道中均匀分布，在电流的回击高度h 上方，电流为0.大地为无穷大电导率的水平面上方的雷电辐射电磁场，在文献［3 -5］中都有研究，本文不再对其详细过程进行推导，只列出雷电流在空间辐射电磁场的计算公式。

式中:r、φ 和z 分别为柱坐标系下的径向坐标、方位角和轴向坐标;Hφ、Er、Ez分别为角向磁场、径向电场、垂直电场;d 是电流偶极子到场点距离;ε0、μ0和c 分别为真空电导率、磁导率及光速;z'表示雷电电流元的坐标。(2)式和(3)式中的右边第1 项为静电场，第2 项为感应场或中间场，第3 项为辐射场或远区场。(1)式右边第1 项为感应场，第2 项为辐射场。

以上采用解析方法推导出了雷电电磁脉冲(LEMP)的表达式，但若直接按上式计算将会非常繁琐，由于军用电站供电电缆是敷地铺设，所以为了简化计算，只关心地表面的雷电电磁场。

文献［6］用解析方法近似推导了地表近区LEMP 一级和二级近似的表达式，并与标准的解析结果进行了对比分析，结果验证了解析推导近似的可行性，证明在电流偶极子到场点距离d ＜50 m 的地表近区，LEMP 场波形与回击通道底部电流波形相似。

图1 雷电回击电磁场模型Fig.1 Model for lightning return stroke electromagnetic field

由于地表近场的电场强度和磁场强度均远高于中远场，所以开展军用电站雷电防护研究需考虑最恶劣的LEMP 情况，将(3)式进行傅里叶变换后计算地表近场的垂直电场强度，观测点P(r，φ，z)在地面上，即z=0，Er=0，从而确立了军用电站可能遭遇的雷电电磁环境参数，如(4)式和(5)式所示。

本文在近场计算中，雷电回击通道高度h=7.5 km，回击速度v =1.3×108m/s.采用脉冲函数作为雷电流函数表达式，用Matlab 和傅里叶变换编程计算出的不同d 处地表近场的电场和磁场强度，分别如图2和图3所示。

可以看出，随着d 的增大，地表近场和磁场的幅值均减小。从图2可知，d=50 m 时，电场精确解的波形与其两级近似解的波形之间存在一定的偏差，随着d 的增大，此偏差也逐渐增加;而从图3可知，d=100 m 时，磁场精确解的波形与其两级近似解的波形有所区分，随着d 的增大，此偏差也逐渐增加。总之，在d ＜50 m 以内电场精确解及在d ＜100 m 以内磁场精确解所对应的波形与各自近似解所对应的波形基本吻合。

2 雷电电磁场与供电电缆的耦合计算

一般地讲，对于场线耦合响应的计算多采用传输线模型［7］，其计算精度能够符合大多数工程应用的需要。目前，最为常用的是Agrawal 等［8］、Taylor等［9］和Rashidi［10］提出的传输线模型，相比之下，Agrawal 模型考虑得最为全面，本文采用Agrawal 模型，如图4所示，结合有限差分法对军用电站电缆的雷电感应过电压开展研究。

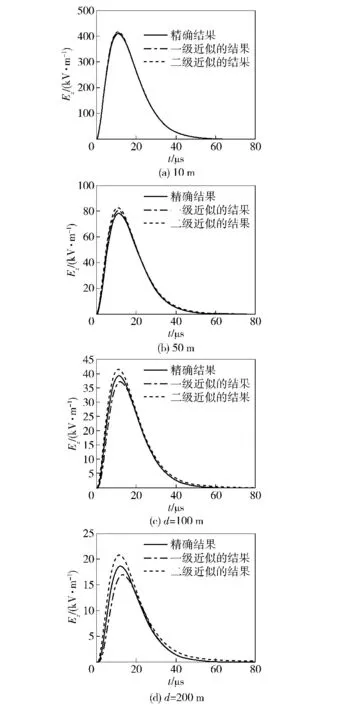
图2 电场波形及其两级近似波形的对比Fig.2 Electric field waveforms and its two-level approximate wave forms

根据Agrawal 传输线耦合模型，方程如下:

边界条件为

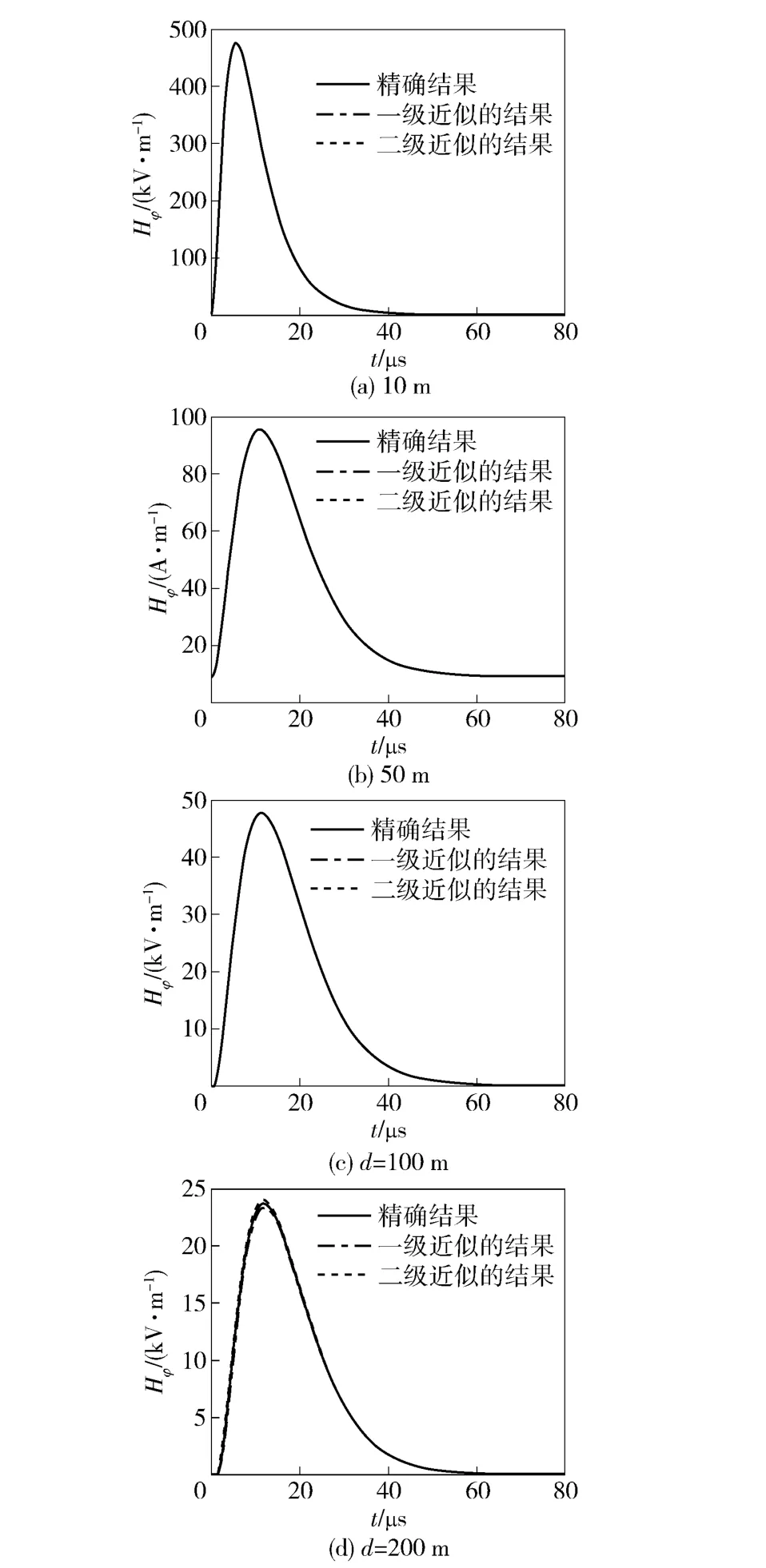
图3 磁场波形及其两级近似波形的对比Fig.3 Electromagnetic F-field waveforms and their two-level approximate wave forms

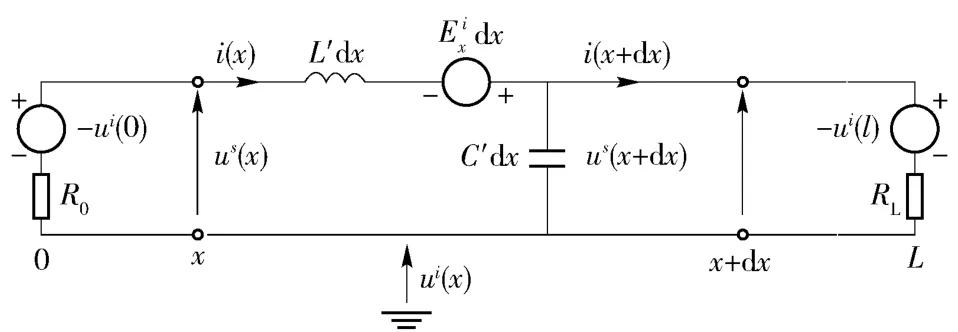
图4 Agrawal 传输线耦合模型示意图Fig.4 Agrawal transmission line model

分别在空间和时间上进行差分，其中Δx 代表空间积分步长，Δt 代表时间积分步长。进行有限差分后，得下式

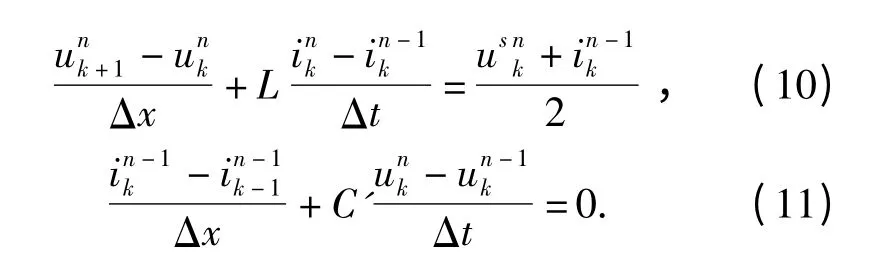
进一步推导，可得到递推表达式:

式中:k 和n 分别表示空间和时间的增量，进一步求解出内部节点、边界节点并确定初始条件，即可求解。

以Agrawal 传输线耦合方程为基础来计算雷电在水平传输线上产生的感应过电压。利用上述模型和方法开展军用电站电缆的雷电感应过电压的研究，重点研究雷电流幅值、电缆长度、电缆高度、电缆端接电阻雷击位置对雷电感应过电压的影响规律，为后续感应雷的防护提供定量分析的基础。

3 军用电站电缆雷电感应过电压耦合规律

图5是依据上述模型计算感应过电压的模型几何图，图中h 为回击通道高度，i(0，t)为通道底部电流，h'为线路高度，L 为导线长度，L1、L2为传输线首末端与雷击点的距离，R0、RL为传输线首末端的终端电阻。计算模型中闪电与传输线的位置由图中D1-D2坐标系确定［11］。

图5 计算雷电感应过电压几何模型图Fig.5 Geometric model of calculated lightinginduced overvoltage

利用Agrawal 模型研究军用电站供电电缆雷电感应过电压的耦合规律。通道底部电流选用两个Heidler 函数来进行拟合，一个典型雷电回击底部电流参数如表1所示，其中I0为通道底部电流幅值，τ1为前沿时间常数，τ2为延迟时间常数，n 为指数。

3.1 雷电流幅值对感应过电压的影响

雷击位置与电缆中心点的垂直距离d1为50 m，导线长度L=100 m，导线直径4 mm.回击通道云底高h =5km，h' =0.5m，两端均接匹配电阻，回击速度v=1.3×108m/s.改变通道底部雷电流幅值时，末端感应电压波形变化情况如图6所示。

表1 典型雷电通道底部电流参数Tab.1 Typical lightning channel-base current

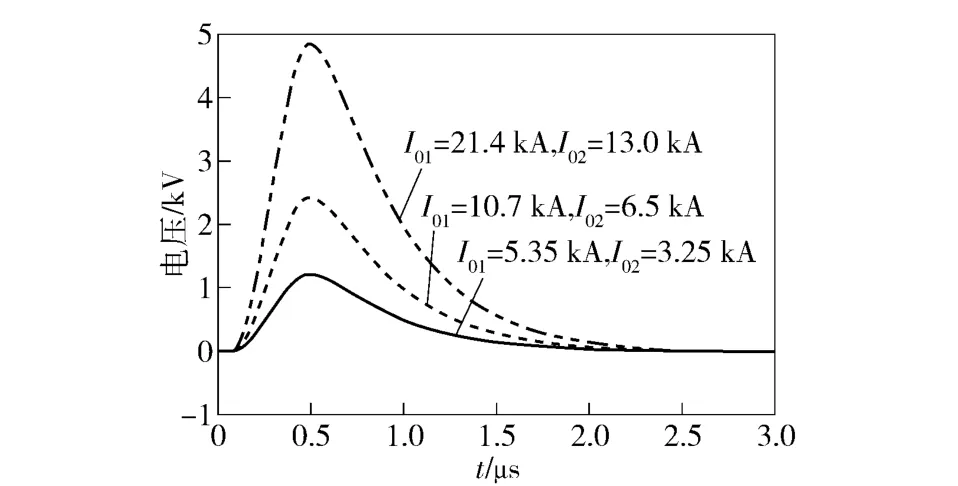
图6 电流幅值对感应电压的影响Fig.6 Effect of current amplitude on induced overvoltage

从图6可以看到，当雷电流幅值呈比例增加时，其产生的雷电感应过电压也呈比例增加，说明电缆雷电感应过电压的大小与雷电流幅值呈正比关系。

3.2 电缆长度对感应过电压的影响

导线两端接匹配电阻，雷击位置与电缆中心点的垂直距离d1为50 m，导线高度h' =0.5 m，导线直径4 mm.回击通道云底高h =5 km，回击速度v =1.3×108m/s.改变导线长度，L 取50 m、100 m、150 m、200 m 时，导线末端的感应过电压如图7所示。

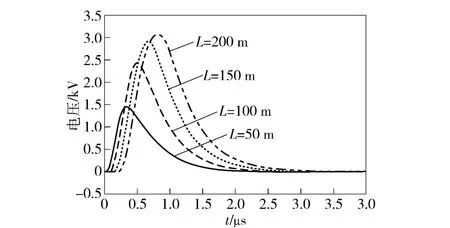
图7 导线长度对感应过电压的影响Fig.7 Effect of L on induced overvoltage

由图7可见，当L 增加时，过电压峰值也增加。当L 从50 m 增加到100 m 时，过电压峰值增加比较大，但当导线长度增加到一定大小时，过电压峰值增加幅度越来越小;对于架空输电线路由于线路比较长，所以当L 增大到一定值时，其值变化对过电压的影响是可以忽略的，但对于军用电站来说，其电缆长度比较短，所以其对感应过电压的影响还是值得关注的。随着导线长度的增加，感应过电压持续时间越来越长，这是在开展感应雷过电压防护时需要关注的。

3.3 电缆高度对感应过电压的影响

导线始端为低阻抗端R =10 Ω，末端接匹配电阻，在d1=50 m，L=100 m，导线直径4 mm 时，回击通道云底高h =5 km，回击速度v =1.3×108m/s，h'取0.1 m、0.2 m、0.5 m 时，导线末端的感应过电压如图8所示。

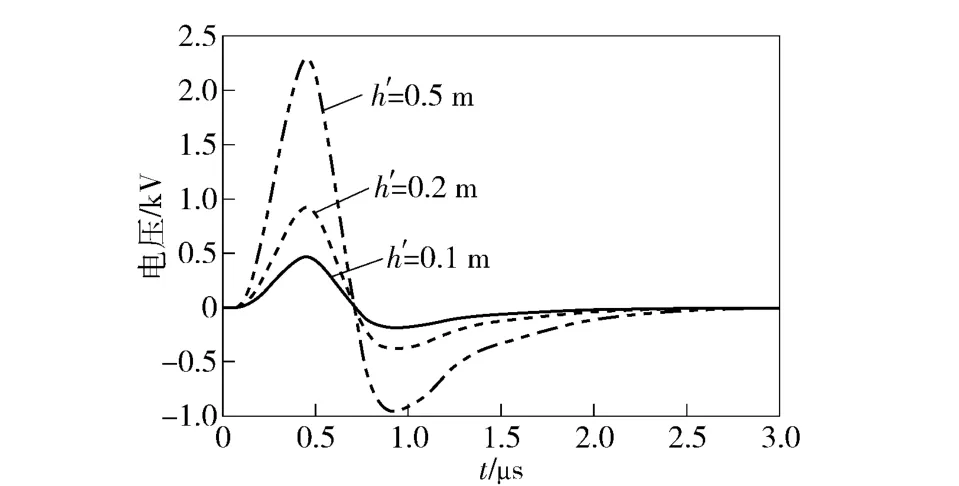
图8 导线高度对感应过电压的影响Fig.8 Effect of h' on induced overvoltage

由图8可以看出，感应过电压大小与高度h'呈一定的正比关系，随着高度h'的增加，感应过电压幅值迅速增加，这是因为离地高，导线和地构成的回路面积大，可以耦合更多的电磁场能量。军用电站的电缆一般是敷地铺设，导线高度h'不会很大，虽然此时的雷电电压并不是很大，但对于敏感设备来说，也会造成影响。

3.4 电缆端接电阻对感应过电压的影响

在d1=50 m，L =100 m，导线直径4 mm，h =5 km，回击速度v =1.3×108m/s，h' =0.5 m 条件下，分别在导线的始末端接不同类型的电阻，其电压波形变化情况如图9所示。从图9中可以看出，当导线两端均接匹配电阻时，其始端和末端电压波形一致;当两端电阻都为匹配电阻或者一端接地、一端接匹配电阻时其波形变化较大。军用电站作为武器装备的能源，是要为武器装备供电的，其中负载大小及负荷结构对其感应过电压是有一定的影响的。

下面重点研究起始端为匹配电阻、末端电阻变化时，模拟末端感应过电压的情况。图10是起始端为匹配电阻，末端分别为100 Ω、200 Ω、1 000 Ω、2 000 Ω时的两端感应过电压波形图，由图10可见，当起始端固定为匹配电阻，末端电阻不断增加的情况下，末端感应过电压值也不断增大，且都为正极性。

通过计算发现，导线两端不同电阻同样对电缆感应过电压波形的大小和极性产生很大的影响，当两端都为匹配电阻或者大电阻时，过电压的波形为单极性，电阻越大其对应的过电压幅值也越大，大电阻大到一定程度时会出现振荡波形;当两端电阻大小差别较大时，高端电阻过电压为双极性，低端为单极性。

3.5 雷击位置对感应过电压的影响

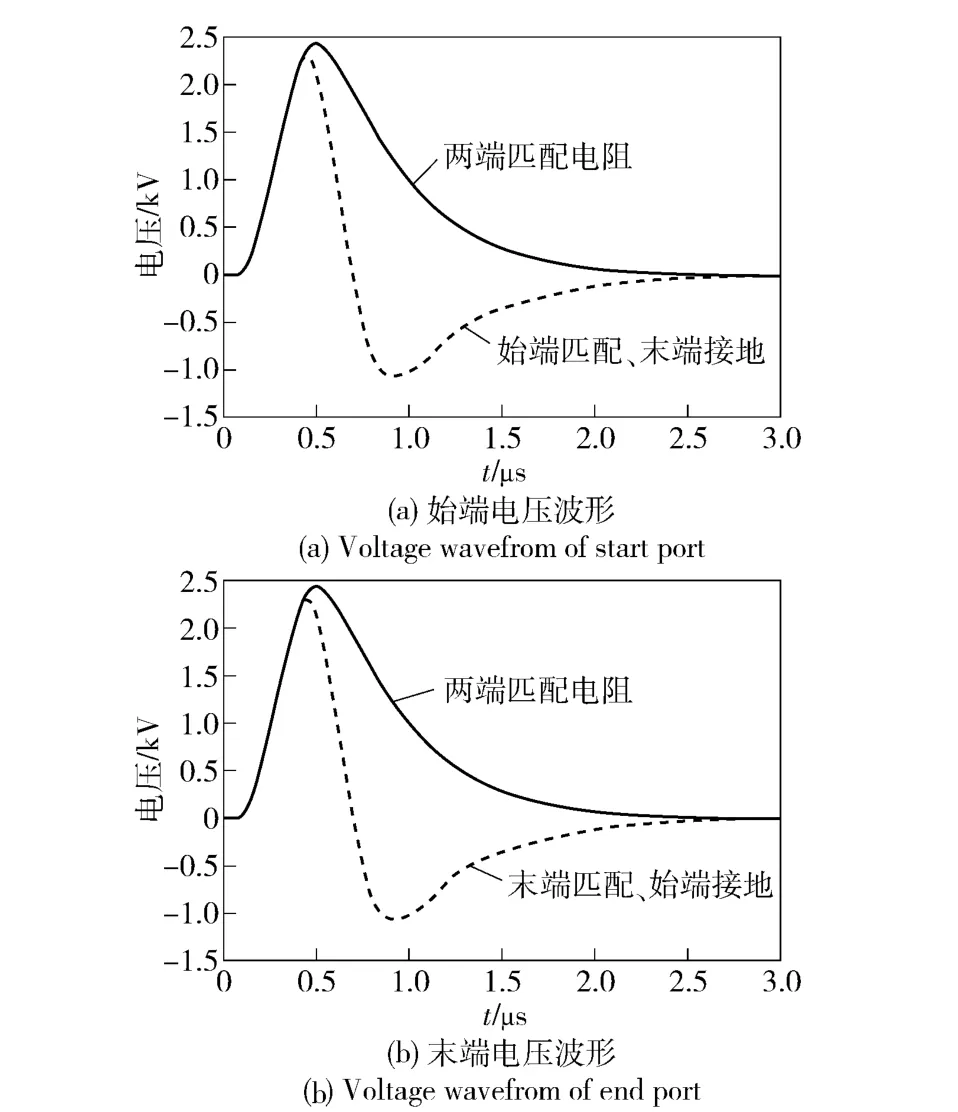
图9 两端电阻不同匹配情况时过电压波形对比Fig.9 Overvoltage waveforms with different resistance

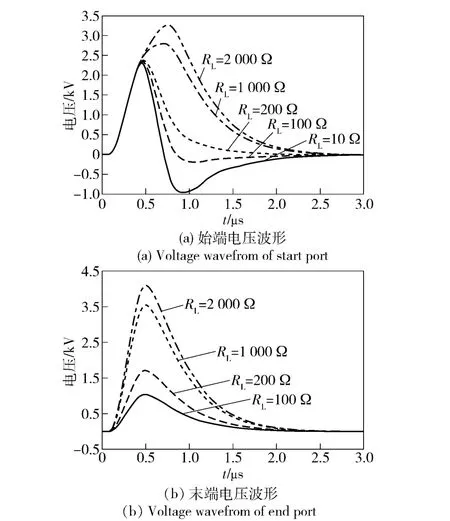
图10 终端电阻对感应过电压的影响Fig.10 Effect of end resistance on induced overvoltage

在L=100 m，导线直径4 mm 情况下，回击通道云底高度h=5 km，h' =0.5 m，始端接地，末端接匹配电阻，回击速度v =1.3×108m/s，雷击水平位置与电缆中心点一致，雷击位置与导线的水平距离d2= -50 m，d1取10 m、20 m、50 m 时，末端感应电压波形变化情况如图11所示。

图11 d1对感应过电压的影响Fig.11 Effect of d1 on induced overvoltage

传输线上雷电引起的感应过电压大小及波形与闪电接地位置密切相关。闪电在导线的垂直方向上距离不断增加时，其感应过电压迅速减小，并不与距离呈正比例关系。下面研究雷击位置与导线水平距离对感应过电压的影响，仿真条件保持不变，d1=50 m，改变d2，取值100 m、0 m、-50 m、-100 m、-200 m 时，末端感应电压波形变化情况如图12所示。

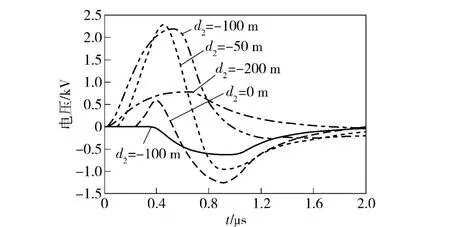
图12 d2对感应过电压的影响Fig.12 Effect of d2 on induced overvoltage

从图12中可看出，闪电在导线水平方向不同位置变化时，过电压不仅大小会发生明显的变化，其极性也在变化，当导线两端接地电阻不同时，闪电在导线两端外侧发生时，高阻端感应过电压会出现大小相等、极性相反的情况。

4 结论

军用电站电缆雷电感应过电压是造成野外军用电站供电系统损坏的主要原因之一。本文根据偶极子模型研究雷电电磁场分布及其规律，提出军用电站电缆雷电感应过电压的计算模型并通过对时间和空间的离散化处理，获取了雷电感应过电压数值计算方法，分析了雷电流幅值、电缆长度、电缆高度、电缆端接电阻、雷击位置对电缆雷电感应过电压的影响规律，得到如下结论:

1)过电压峰值大小与雷电流幅值、电缆高度、电缆长度呈一定的正比例关系，但当电缆长度增加到一定大小时，过电压峰值增加幅度越来越小。

2)电缆端接电阻对过电压波形的大小和极性产生很大的影响，当始端为匹配电阻，末端感应过电压值随着末端电阻的增大而不断增大。

3)闪电在电缆的垂直方向上距离不断增加时，其感应过电压迅速减小，并不与距离呈正比例关系;闪电在电缆水平方向不同位置变化时，过电压大小和极性均发生变化，从而为军用电站雷电感应过电压的防护提供理论参考依据。

References)

［1］ Rubinstein M，Uman M A.Methods for calculating the electromagnetic fields from a known source distribution:application to lightning［J］.IEEE Transactions on Electromagnetic Compatibility，1989，31(2):183 -189.

［2］ Farhad R，Marcos R，Silvia G，et al.Voltages induced on overhead lines by dart leaders and subsequent return strokes in natural and rocket-triggered lightning［J］.IEEE Transactions on Electromagnetic Compatibility，1997，39(2):160 -166.

［3］ Lin Y T，Uman M A，Tiller J A，et al.Characterization of lightning return stroke electric and magnetic fields from simultaneous two-station measurements［J］.Journal of Geophysical Research:Ocean＇s，1979，84(C10):6307 -6314.

［4］ Cooray V.Underground electromagnetic fields generated by the return stroke of lightning flashes［J］.IEEE Transactions on Electromagnetic Compatibility，2001，43(1):75 -84.

［5］ 陈亚洲，刘尚合，魏明，等.雷电电磁场的空间分布［J］.高电压技术，2003，29(11):1 -2.CHEN Ya-zhou，LIU Shang-he，WEI Ming，et al.Distribution of LEMP above ground level［J］.High Voltage Engineering，2003，29(11):1 -2.(in Chinese)

［6］ 陈亚洲，肖雪荣.地表近场LEMP 与回击电流的近似性［J］.高电压技术，2007，33(12):23 -26.CHEN Ya-zhou，XIAO Xue-rong.Characteristic of approximation between LEMP in near area and channel-base current［J］.High Voltage Engineering，2007，33(12):23 -26.(in Chinese)

［7］ 倪谷炎，罗建书，李传胪.Taylor 与Agrawal 模型的解析求解与模型比较［J］.强激光与粒子束，2007，19(9):1521 -1525.NI Gu-yan，LUO Jian-shu，LI Chuan-lu.Comparison of Taylor and Agrawal coupling models and their analytic solutions［J］.High Power Laser and Particle Beams，2007，19(9):1521 -1525.(in Chinese)

［8］ Agrawal A K，Price H J，Gurbaxani S H.Transient response of multiconductor transmission lines excited by a nonuniform electromagnetic field［J］.IEEE Transactions on Electromagnetic Compatibility，1980，22:119 -129.

［9］ Tay1or C D.Satterwhite R S，Harrison C W.The response of a terminated two-wire transmission line excited by a nonuniform electromagnetic field［J］.IEEE Transactions on Antennas Propagat，1965，13:987 -989.

［10］ Rachidi F.Formulation of the field-to-transmission line coupling equations in terms of magnetic excitation field［J］.IEEE Transactions on Electromagnetic Compatibility，1993，35(3):404-407.

［11］ Nucci C A，Rachidi F，Ianoz M，et al.Lightning-induced voltage on overhead lines［J］.IEEE Transactions on Electromagnetic Compatibility，1993，35(1):75 -86.