时域传输线方程随机负载问题多项式混沌分析

杨 蕾，陈韦韦，闫丽萍，赵 翔

(四川大学 电子信息学院，四川 成都 610065)

0 引言

传输线是传递信息和能量的重要载体，是电子电气设备的重要组成部分。由于电子设备工作的环境，例如气候因素[1]、机械因素或者电磁干扰等复杂多样[2-4]，使得传输线连接的负载随机变化，因此，研究负载随机问题对于时域传输线方程的影响很有必要。

目前,对于随机传输线问题的典型研究方法是蒙特卡罗方法和多项式混沌方法[5]。蒙特卡罗方法主要是通过对随机模型参数进行大量采样和实验来获得随机响应[6-8]，该方法的优点在于容易实现，但是同时具有工作量大、计算时间长等缺点[9]，张瑛[10-11]等人利用蒙特卡罗方法分析了传输线制造工艺参数随机变化对传输线传输性能的影响。多项式混沌方法[12-14]主要是通过随机变量的概率分布，利用正交多项式混沌对于随机变量和随机响应进行展开，结合随机Galerkin方法将随机方程转变为确定性方程组进行求解，进而可以获得随机响应[15-16]。程市[17]等人利用多项式混沌方法对传输线的加工材料和结构参数随机不确定性对传输性能的影响进行了研究，文献[18]利用多项式混沌分析方法对传输线的高度随机不确定性对传输线响应进行了研究，李湛宇[19]等人利用多项式混沌分析方法对辐射场的不确定变量对传输线响应的影响进行分析。但是上述文献都没有研究随机负载对传输线响应的影响，所以本文提出利用多项式混沌分析方法对负载随机不确定性对传输线响应的影响进行分析。

本文利用多项式混沌分析方法对时域传输线方程随机负载问题进行分析，并通过实例计算，将多项式混沌分析与蒙特卡罗方法的统计信息结果进行对比来验证本文方法的正确性和高效性。

1 时域传输线方程随机负载问题的多项式混沌分析

以单导体传输线模型为例，含有电压源和随机负载的传输线电路如图1所示。

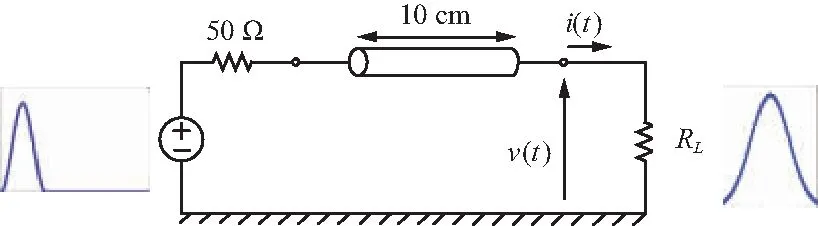
图1 含源和随机负载的传输线电路Fig.1 Circuit diagram of transmission line with source and random load

传输线远端电阻RL=μL+σLξ，ξ为随机变化参数，满足标准正态分布，μL，σL分别为RL的均值和标准差。具有随机参数ξ的时域传输线方程表达式[20]为：

(1)

(2)

式中，l为单位长度电感；c为单位长度电容。

利用标准Hermite正交多项式对电压响应v(z，t，ξ)和电流响应i(z，t，ξ)进行多项式混沌展开。由于二阶展开在大多数情况下是足够精确的，因此在本文的其余部分中，如果没有另外指定，则在多项式展开中将忽略高次多项式[18]。

v(z，t，ξ)≈v0(z，t)φ0(ξ)+v1(z，t)φ1(ξ)+

v2(z，t)φ2(ξ)，

(3)

i(z，t，ξ)≈i0(z，t)φ0(ξ)+i1(z，t)φ1(ξ)+

i2(z，t)φ2(ξ)，

(4)

式中，v0，v1，v2，i0，i1，i2是多项式系数，前3个基于标准正太分布的Hermite正交基函数为：

φ0=1，

(5)

φ1=ξ，

(6)

(7)

Hermite内积满足：

(8)

式中，w(ξ)为随机变量ξ的概率密度函数；当m=n时，δmn=1，否则δmn=0。

本文以传输线第一个方程为例，将式(3)和式(4)带入式(1)中变换整理有：

(9)

对式(9)使用随机Galerkin方法进行处理[21]，即使用φm(ξ)(m=0，1，2)和等式两边做内积：

(10)

式(10)可表示为：

(11)

式中，m=0，1，2。类似传输线第二方程可表示为：

(12)

式中，m=0，1，2。

通过使用上述方法可将式(1)和式(2)转化为如下形式：

(13)

(14)

式中，

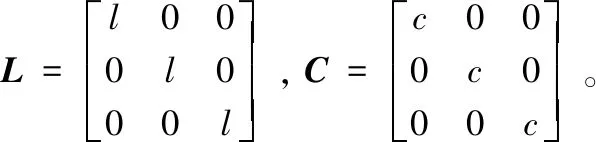
可以看到原问题表达方程式(1)和式(2)将转换为式(13)和式(14)所示的三导体传输线问题，单导体的分布参数与单位矩阵的乘积即为三导体的参数矩阵。

考虑负载边界条件：

(15)

利用标准Hermite正交多项式对远端电阻RL(ξ)进行多项式混沌展开，如下：

RL(ξ)≈r0φ0(ξ)+r1φ1(ξ)+r2φ2(ξ)。

(16)

将式(1)、式(2)和式(16)带入式(15)可得：

(17)

对式(17)进行随机Galerkin方法处理，即使用φm(ξ)(m=0，1，2)和等式两边做内积：

(r0α00m+r1α10m+r2α20m)i0(z，t)|z=L+

(r0α01m+r1α11m+r2α21m)i1(z，t)|z=L+

(r0α02m+r1α12m+r2α22m)i2(z，t)|z=L=

vm(z，t)|z=L，

(18)

式中，αknm=〈φk(ξ)φn(ξ)，φm(ξ)〉=

m=0，1，2。

将式(18)进一步变换整理可得：

(19)

式中，R=r0A0+r1A1+r2A2，

使用多项式混沌分析方法，将随机负载条件下的时域传输线方程式(1)和式(2)转变为由式(13)、式(14)和式(19)组成的关于电压响应和电流响应的正交多项式展开系数的确定性方程组问题，即构成了一个三导体传输线问题，如图2所示。

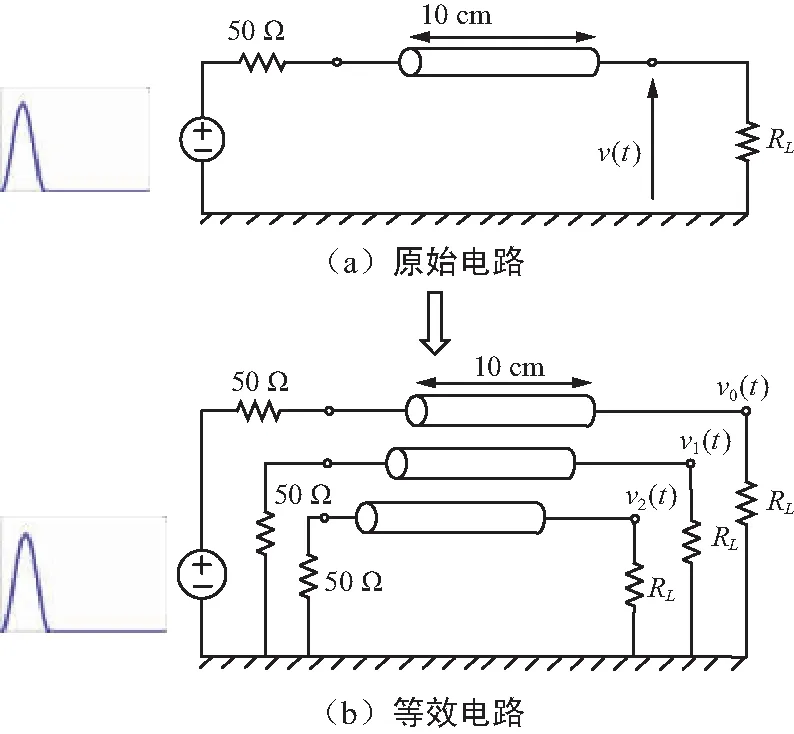
图2 含源和负载的传输线电路Fig.2 Circuit diagram of transmission line with source and load

由文献[18]可知，利用等效电路图中三导体传输线远端电压可以获得随机响应电压的均值和标准差为：

E{v(t)}=v0(t)，

(20)

(21)

2 算例与分析

以图1所示的含源和随机负载的传输线电路为例，对时域传输线方程随机负载问题的多项式混沌分析进行实例计算，将所得结果与蒙特卡罗方法的计算结果进行对比。

算例1的传输线长L=10 cm，半径r=0.5 mm，远端电阻RL=μL+σLξ，ξ满足标准正态分布，均值μL=50 Ω，标准差σL=10 Ω。激励电压波形如图3所示。

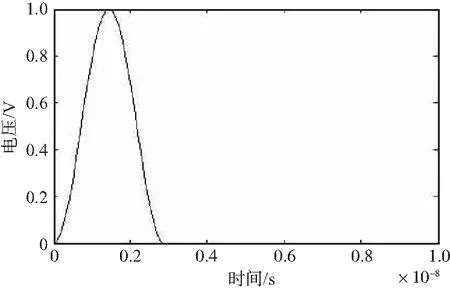
图3 算例1激励电压波形Fig.3 Excitation voltage waveform of example 1

计算在该随机电阻边界条件下的传输线远端电压响应的统计信息，如图4所示。

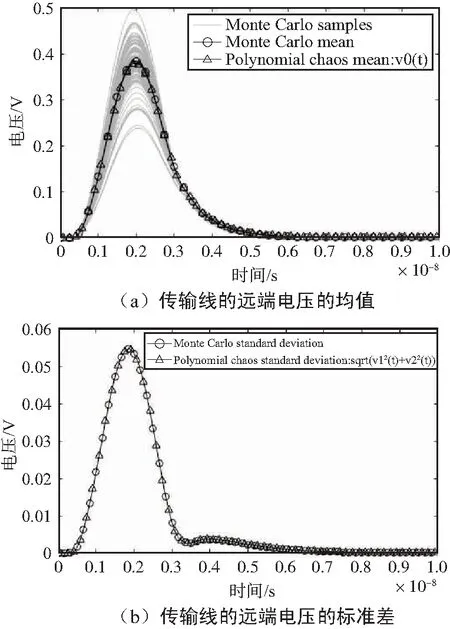
图4 算例1传输线的远端电压随机分析Fig.4 Random analysis of the far-end voltage of the transmission line in example 1

算例2的传输线长L=20 cm，半径r=0.5 mm，远端电阻RL=μL+σLξ，ξ满足标准正态分布，均值μL=50 Ω，标准差σL=10 Ω。激励电压波形如图5所示。

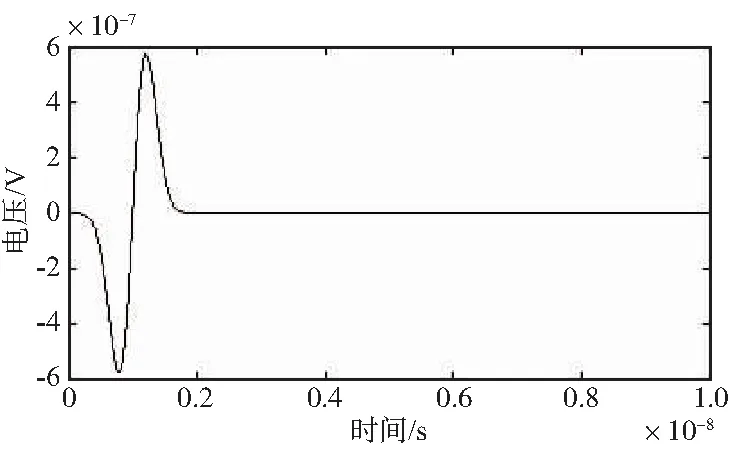
图5 算例2激励电压波形Fig.5 Excitation voltage waveform of example 2

计算在电阻边界条件下的传输线的远端电压响应的统计信息，如图6所示。图4(a)和图6(a)分别是算例1和算例2的传输线远端电压响应的均值对比图，图4(b)和图6(b)分别是算例1和算例2的传输线远端电压响应的标准差对比图，其中，灰色线条是100次蒙特卡罗方法的结果，圆圈标注的黑色线条是100次蒙特卡罗方法的统计信息结果，三角形标注的黑色线条是多项式混沌分析方法的统计信息结果，可以看出蒙特卡罗方法的结果和多项式混沌分析的结果一致，同时多项式混沌分析计算时间仅为蒙特卡罗方法的计算时间的9%，说明了本文针对时域传输线方程随机负载问题的多项式混沌分析方法的正确性和高效性。

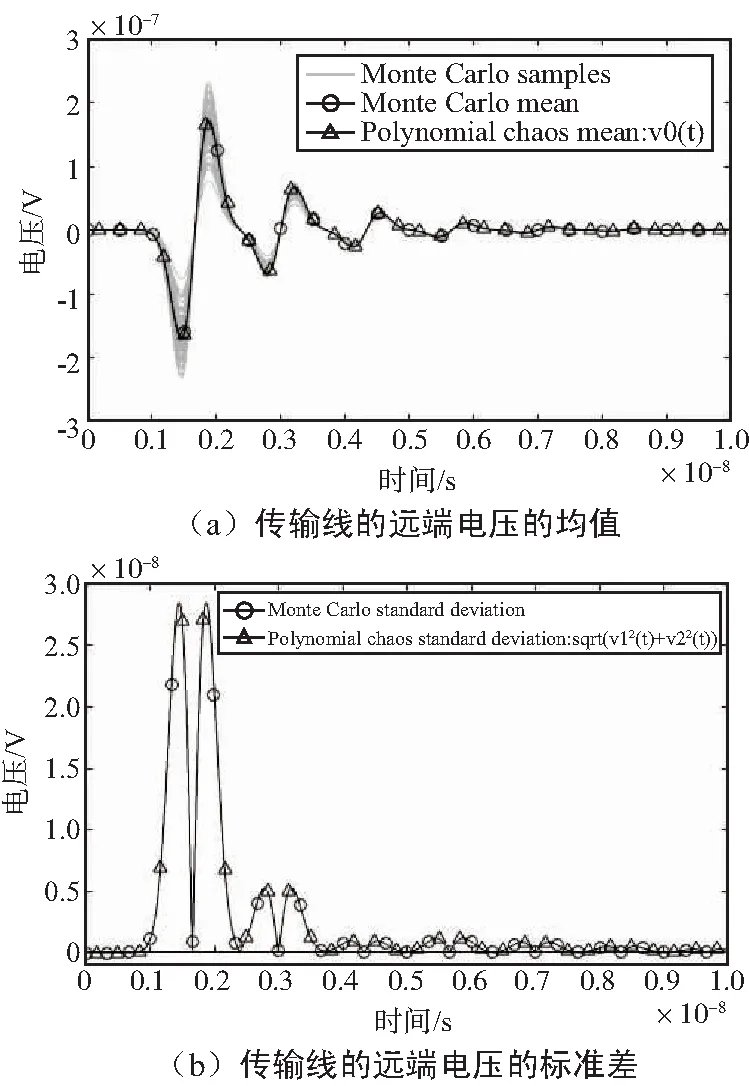
图6 算例2传输线的远端电压随机分析Fig.6 Random analysis of the far-end voltage of the transmission line in example 2

3 结束语

本文将多项式混沌方法引入到时域传输线方程的随机负载问题中，将随机负载条件下的时域传输线方程转化为一个关于电压响应和电流响应的正交多项式展开系数的确定性方程组问题，通过实例计算，将多项式混沌分析的结果与蒙特卡罗方法的结果进行对比，结果显示2种分析方法对于随机电压响应的均值和标准差结果完全一致，同时多项式混沌分析方法的计算时间是蒙特卡罗方法的9%，证明了本文提出的针对时域传输线方程随机负载问题多项式混沌分析方法的正确性和高效性。