三轴天线系统外测精度修正方法研究

王东升，张 垚，高 菲，黄立娜，杨俊武，张建辉，付树洪

(1.中国西安卫星测控中心，陕西 西安 710043；2.宇航动力学国家重点实验室，陕西 西安 710043；3.中国太原卫星发射中心，山西 太原 030100)

0 引言

近年来，卫星发射数量逐年增多，商业航天方兴未艾，在轨卫星急速增加，对卫星地面站的要求越来越高。为实现地面站卫星测控与遥感卫星数据接收一体化多功能的需求，同一台天线系统既要有较高的测量精度，又要有全空域高精度的跟踪[1-2]。带有斜转台的三轴天线是一种较好的选择，这种结构的天线在遥感卫星数据接收站大量使用，可以实现对任意轨道倾角的卫星全空域无盲区高精度跟踪[3]。相比卫星应用数据接收系统，测控系统不仅仅要关注数据接收，同时还要更关注测距、测速和测角数据的准确性[4]，以便中心对目标进行精确定轨[5]。因此，对其测角[6]、测距、测速精度[7]提出更高要求。

与传统的方位俯仰型两轴天线相比，最大差异表现在2个方面：一是天线三轴中心(指天线方位轴、俯仰轴和电轴交点)位置在测站地平坐标系里随第三轴的角度位置移动，标定距离零值和角度零值时要考虑这种特殊性；另一方面是天线有3个旋转轴，轴角编码测量数据与测站地平坐标系的方位角及俯仰角存在非线性变换关系，引入新的角度误差系数和角度误差系数标定难度增大[8]。

科研人员采用射电星标校、在轨卫星标校和无人机标校等标校理论对三轴天线角度误差的标定做了大量研究，取得了不少成果[9]。由于传统卫星测控领域对外测数据的要求较高，采用三轴天线后如果不进行必要的修正，所得数据是不可用的。本文主要针对该问题，通过分析三轴天线的结构，建立合理的坐标系，提出了相应的数据修正的数学方法，并通过实际跟踪卫星验证了外测数据修正方法的可行性。

1 三轴天线结构

三轴天线结构自上而下为俯仰轴、方位轴和第三轴，其中第三轴倾斜角度为α，三轴天线结构示意如图1所示。

图1 三轴天线结构示意Fig.1 Structure of the tri-axial antenna

在任务执行前，天线控制单元根据理论弹道，首先将第三轴置于适当位置，在此过程中，第三轴围绕oo’转动，o’点围绕o点旋转，待第三轴置位完成，o’在任务执行过程中保持不动，方位和俯仰围绕o点在转动[10-11]。三轴天线旋转模型如图2所示。方位围绕o’o”旋转，第三轴围绕oo’转动。

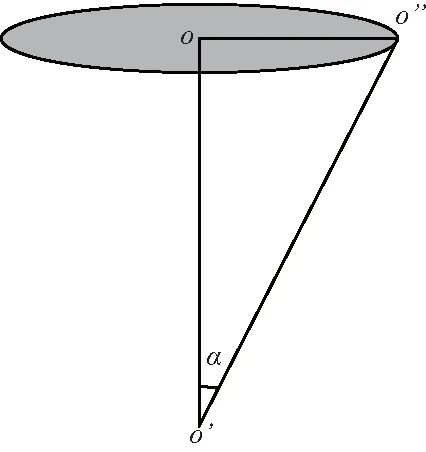
图2 三轴天线旋转模型Fig.2 Rotation model of tri-axial antenna

其中o’为第三轴预埋环中心圆点，o”点为方位轴和俯仰轴交点(相位中心)，o为第三轴预埋环中心圆点和地心延长线与o”旋转面的交点。

因此，三轴天线的方位轴和俯仰轴交点(相位中心)的位置会随不同任务在以o为圆心、oo”为半径的圆上变化。

目标在地平直角坐标中的坐标示意如图3所示。三轴天线大地坐标系与测量坐标系不重合，为使三轴天线大地坐标系更接近AE轴天线大地坐标系，设三轴天线大地坐标系为以o为原点的XYZ坐标系，测量系统坐标系统是以o”为原点的XcYcZc坐标系。

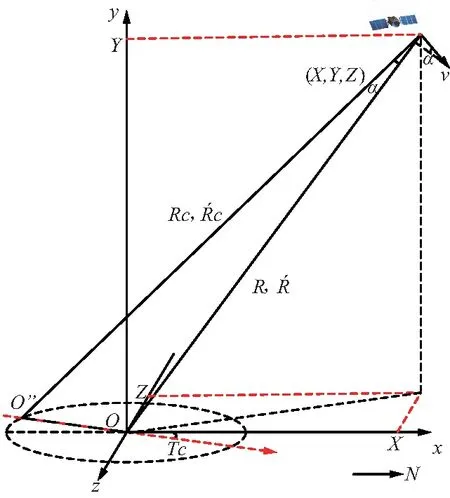
图3 目标在地平直角坐标中的坐标示意Fig.3 Schematic diagram of the target in the horizontal rectangular coordinate system

o，o’，o”的关系为：o’为大地测量点，第三轴预埋环中心圆点；o”为方位轴与俯仰轴的交点，即天线的相位中心点；o为o”在Z轴上的投影。

2 坐标系的定义

2.1 直角坐标与极坐标的转换关系

直角坐标与极坐标的转换关系如下：

(1)

(2)

(3)

2.2 测量系与地平系的坐标变换

取方位轴天线座高度为h，即三轴中心到斜转台中心的直线距离为h。斜转台倾斜角为θ，三轴中心与测站地平坐标系圆点处在同一个基准面，三轴中心绕测站地平坐标系Y轴旋转[12-14]，半径为hsinθ，在测站地平坐标系的直角坐标是(hsinθcosTc，0，hsinθsinTc)。

测量坐标系与地平坐标系通过斜转台交联在一起，假设斜转台的倾角是θ，目标在测量坐标系内的角位置用Ac，Ec，Tc表示(Tc是斜转台Xc轴在大地水平面投影与真北的夹角)，在地平极坐标系的角位置用Az，El示。按照坐标系定义，其位置关系可表示为：

(4)

(5)

(6)

3 三轴天线误差模型

常见的方位俯仰型天线座的角度标校的误差模型已经较为成熟，通过射电星标校方法有效提高了天线指向精度。转台式三轴天线其实质为方位-俯仰型座架安装在转动的倾斜面上，其误差项与方位-俯仰型座架基本一致，但斜转台三轴天线第三轴的引入，又增加了第三轴角度零值误差和倾斜台角度误差2个误差项。

与方位俯仰型两轴天线相比，影响三轴天线指向精度的误差源除了方位俯仰角度零值误差、大盘不水平误差、轴系误差、重力下垂和大气折射引起的误差外，还包括斜转台的角度零值误差和斜转台倾斜角误差。三轴天线误差模型建模时，大地不水平误差在地平坐标系建模，其模型与方位俯仰型天线的误差模型一致；方位俯仰角度零值误差和轴系误差在测量坐标系建模，其模型与方位俯仰型天线的误差模型一致；重力变形和大气折射在测量坐标系建模比较容易理解，考虑到斜转台倾斜角较小，重力变形系数和大气折射系数对测量系方位角的影响忽略不计，对测量系俯仰的误差用地平坐标系俯仰角修正。所以重力变形和大气折射误差模型与方位俯仰型天线的误差模型形式一致，斜转台的影响在把测量系角度转换到大地系的过程中考虑。按照该思想，在测量系，方位俯仰的测量系真值(电轴指向)表示为[9，15]：

A#=AC+A0+δ.tanEC+KbsecEC，

(7)

E#=Ec+E0+EgcosE+EdcotE。

(8)

考虑到斜转台倾斜角较小，式中E=Ec+θ0cosAc。

斜转台的误差模型为：

T=Tc+t0，

(9)

θ=θ0+Δθ，

(10)

式中，T为斜转台的角度真值；Tc为斜转台编码器读数；T0为零值误差；θ为斜转台倾斜角真值；θ0为斜转台倾斜角理论值；Δθ为斜转台倾斜角误差。

利用天文学的坐标变换方法计算出星组在某一地点观测时刻的方位和俯仰角(A，E)，通过标校计算机引导天线指向空域中的射电星，进行十字扫描。根据功率最大值信息进行数据分析处理，解算出某一恒星在观测时刻实际测量的方位和俯仰角(Ac，Ec)，2组数据进行比较得出ΔA，ΔE。通过多次测量，利用最小二乘法或其他方法得到指向误差模型修正参数。

4 三轴天线外测修正算法

4.1 测角修正方法

通过误差模型的分析，可以得到修正后的测站测量系的方位俯仰测角数据(电轴指向)、斜转台角度和斜转台倾角。

进行测量系到大地系的转换：

(11)

实现测站地平极坐标系的测角数据修正：

Az=Az+θMsin(Az-AM)*tanEl，

(12)

Ez=El+θMcos(Az-AM)，

(13)

(14)

(15)

(16)

式中，角度Agz和Egz即为测站基于地平系测角数据。

4.2 测距修正方法

目标在测站地平直角坐标系(o为原点)中的坐标为(X，Y，Z)。由图3可得径向距离R：

(17)

通过式(12)和式(13)得到基于大盘水平面(以o”为原点)以上的电轴指向(Az，Ez)。通过式(9)得到修正后的三轴方位角。通过式(14)，将大地系(以o”为原点)的极坐标系平移并转化为测站地平直角坐标系。再利用式(11)即可计算得出径向距离R。

因此，修正测控基带的径向距离R时，需要天线系统将通过式(12)和式(13)修正的Az，Ez数据以及通过式(9)修正的T数据发送至测控基带。测控基带根据实时测量的距离值，通过式(14)和式(17)得到修正后的径向距离，并发送至测控中心。

4.3 测速修正方法

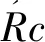
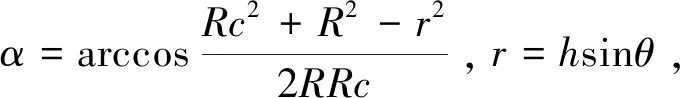
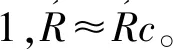
由以上分析可以看出，三轴天线由第三轴偏轴带来的测距、测速及测角处理方式与传统测控系统不同，必须将测量系的测距、测速及测角测量结果进行修正转换到大地坐标系，同时测距、测速修正与三轴天线的测量系方位角Ac、测量系俯仰角Ec和倾斜轴方位角Tc都有关系，因此，系统内部接口中需增加ACU与基带的接口，用于ACU向基带上报任务过程中实时的测量系方位角Ac、测量系俯仰角Ec和倾斜轴方位角Tc。

5 工程应用结果分析

依托12 m Ka/X/S三频段地面测控数传接收系统开展了测控外测修正试验。试验前采用射电星标校方式对天线角度进行了标校，其全空域指向精度满足Ka频段的捕获要求。

2019年6月的实际跟踪卫星进行了验证，三轴天线跟踪俯仰最大角度为12°，基带分系统、天线分系统分别对测距、方位和俯仰数据进行修正，修正后的结果如图4和图5所示。对结果数据与卫星精确定轨后的理论弹道数据进行了比对，分析出该三轴天线地面站系统测控外场精度如表1所示。满足对标准TT&C测控模式下，测距随机误差小于10 m，测角随机误差小于100″的要求。

图4 外测数据修正后数值Fig.4 Orbit measurement data after modification

图5 外测数据与精轨差值Fig.5 Difference between precision tracking data and orbit measurement data after modification

表1 误差修正后的外测精度
Tab.1 Orbit measurement precision after modification

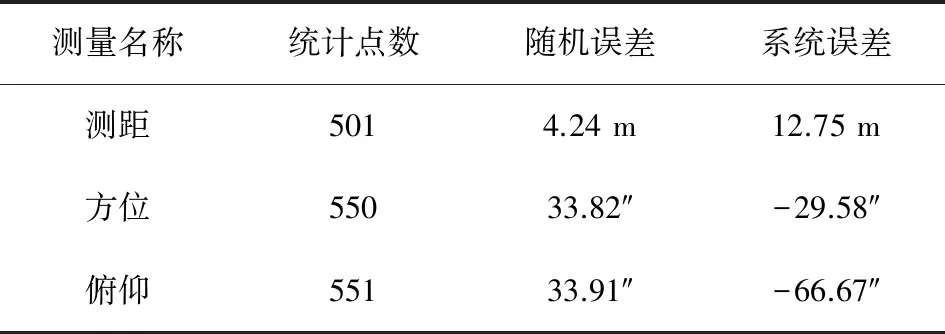
测量名称统计点数随机误差系统误差测距5014.24 m12.75 m方位55033.82″-29.58″俯仰55133.91″-66.67″

针对高、中、低轨目标，各测控体制分别进行了20余圈次的验证，从经过修正后外测与精密轨道弹道数据比对的系统误差和随机误差看，采用该修正方法对三轴天线测控系统外测数据进行修正的效果良好，数据可参与后续卫星精密定轨。

6 结束语

为实现地面站卫星测控与遥感卫星数据接收一体化多功能的需求，同一台天线系统既要有较高的测量精度，又要有全空域高精度跟踪的需求，考虑使用具有斜转台的三轴天线系统。本文阐述了三轴天线在高精度外测数据的劣势，并分析了三轴天线的特性，通过分析三轴天线的结构，建立合理的坐标系，提出了相应的数据修正的数学算法。

通过12 m Ka/X/S三频段地面测控数传接收系统开展了三轴天线测控外测修正试验，试验结果表明该方法有效可行，具备进行推广应用的价值。