一种用户级多波束卫星系统预编码算法

陶 凯，孙 哲

(1.中国电子科技集团公司第五十四研究所，河北 石家庄 050081；2.海军驻邯郸地区军事代表室，河北 邯郸 056000)

0 引言

卫星通信系统在军事通信中发挥着重要作用[1-4]，波束间频率复用可有效地提高频带利用率，能够实现卫星系统的高吞吐量通信[5-6]。基于全频率复用方案的多波束卫星系统可建模为一种分布式多输入多输出(Multiple-Input Multiple-Output，MIMO)系统[7]，因此可将陆上MIMO系统预编码相关技术用于多波束卫星系统前向链路，以提高前向链路的容量。现有基于信漏噪比(Signal-to-Leakage-and-Noise Ratio，SLNR)[8]和块对角化(Block Diagonalization，BD)的预编码[9]方案虽然可有效地降低同道干扰，且对接收天线数目没有限制，但接收矩阵的求解需要获知预编码矩阵。为此可利用脏纸编码(Dirty Paper Coding，DPC)的思想，来抵消同一用户的码流间互扰。文献[10]提出一种基于连续信漏噪比(Successive Signal-to-Leakage-Plus-Noise Ratio，SSLNR)的BLR-SSLNR-THP算法，但当用户有多个码流时，其第一个码流的信道增益最大，最后一个码流的信道增益最小，导致系统误比特率(Bit Error Rate，BER)性能较差。为此，文献[11]提出一种基于各天线的PA-SSLNR算法，在每个用户的各天线上独立计算SSLNR值。本文在PA-SSLNR算法的基础上，基于对多波束卫星系统信道特性的分析，提出了用户级的SSLNR算法——US-SSLNR算法，能够有效地降低各用户间的增益差，从而有效提高预编码算法的误比特率性能，且计算法复杂度较低。

1 系统模型

1.1 波束辐射方向图建模

现对Ka波段多波束卫星系统的前向链路建模。由于地面站采用大功率天线且无遮挡，因此该传输路径可视为理想路径。因此只需考虑卫星到用户的下行链路。假定卫星一簇波束共有K个，多波束卫星系统一簇19波束示意如图1所示，单波束的辐射方向图函数如式(1)所示[12]。

图1 多波束卫星系统一簇19波束示意Fig.1 Diagram of multi-beam satellite system with 19 beams in a cluster

(1)

式中，

可见，波束19中发送的信号对波束1中的用户影响很小，可忽略不计。

1.2 系统建模

若多波束卫星系统采用全频率复用方案及时分多址方式，即每个波束共用一个频段，且采用TDMA方式随机选择一个用户进行通信。因此，多波束卫星系统可建模为卫星MIMO系统。

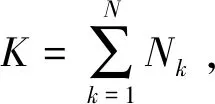
(2)

T=[T1T2...TN]，

(3)

(4)

则式(2)可以表示为：

yk=HkTs+nk。

(5)

2 算法原理

借鉴文献[11]提出的陆地MIMO系统基于各天线的PA-SSLNR算法，在卫星MIMO系统中，对用户分组以后，当组内码流数和其用户数相等时，通过式(2)，可以得到第k组的第j个用户的接收信号为：

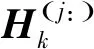
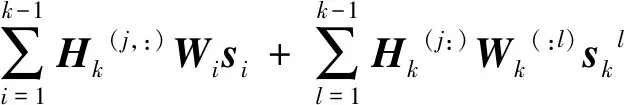
式中，

因此，预编码矩取自矩阵对{Hk(j：)，HHk(j：)，Hkj，HHkj+σ2nINT}的最大的广义特征值所对应的广义特征向量，同时满足发送功率限制tr(Wk(：j)，HWk(：j))=1。

假设对K=19情形分为3组：

则第1组用户的接收信号为：

(6)

(7)

因此，式(5)变为：

得到预编码矩阵之后，需要从发端抵消掉已知的泄漏。所有用户的预编码矩阵联合起来得到：

W=[W1…WN]。

经过预编码之后所有用户等效的信道矩阵为：

最大化SSLNR之后，R的上三角元素的值相对于R的其他元素的值是比较小的，可以近似认为R是一个下三角矩阵。

因此，与THP类预编码一样，可得：

采用THP预编码方法，在发送端抵消掉已知的泄漏，系统框图如图2所示。

图2 US-SSLNR预编码系统框图Fig.2 System diagram of US-SSLNR precoding algorithm

3 复杂度分析

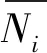
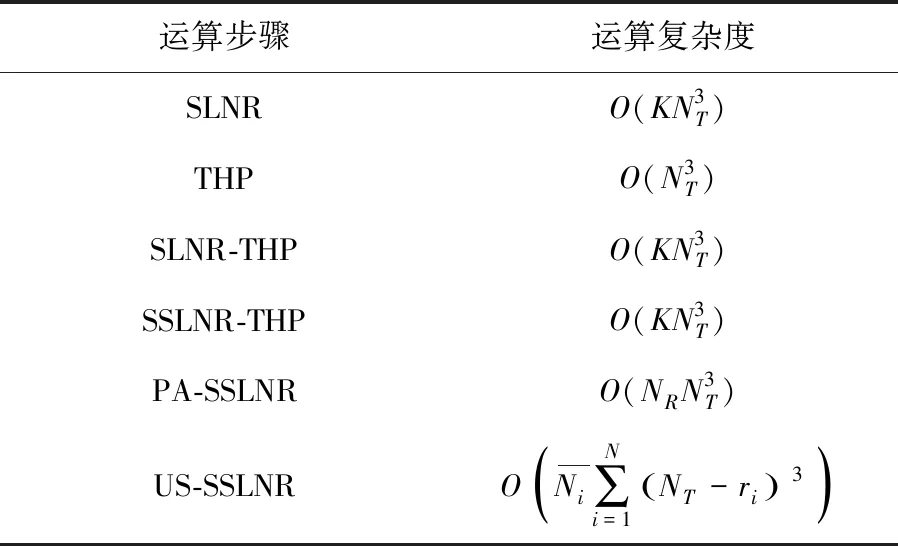
表1 各种预编码算法的复杂度
Tab.1 Complexities of several precoding algorithms

运算步骤运算复杂度SLNRO(KN3T)THPO(N3T)SLNR-THPO(KN3T)SSLNR-THPO(KN3T)PA-SSLNRO(NRN3T)US-SSLNRO(Ni∑Ni=1NT-ri()3)

由表1可以看出，相比SSLNR-THP算法和PA-SSLNR算法，US-SSLNR算法有较低的计算复杂度，且随着分组数的增大或参数ri的增大而减小。

4 算法性能仿真

对多波束卫星MIMO系统采用蒙特卡洛方法进行系统性能仿真，仿真模型参数[14]如表2所示。

表2 多波束卫星系统模型参数
Tab.2 Model parameters of multi-beam satellite system

参数取值卫星轨道高度35 786 km频带Ka (20 GHz)波束数19半功率波束宽度0.6°降雨衰落均值-2.6 dB降雨衰落方差1.63 dB调制方式16QAM

对K=19个用户按第2节的方式进行分组，并将仿真结果与SSLNR-THP算法、PA-SSLNR进行对比，如图3所示。

图3 算法性能仿真Fig.3 Simulation diagram of algorithm performance

由图3可知，在低信噪比区域，3种算法的误码性能相当。随着信噪比的提升，在中信噪比区域，本文算法和PA-SSLNR算法的误码率性能相当，均优于SSLNR-THP算法。在高信噪比区域，本文算法和PA-SSLNR算法的误码率性能仍然相当，均优于SSLNR-THP算法，性能提升大约4.7 dB。这是由于本文算法和PA-SSLNR算法能有效降低各个用户之间的增益差。

5 结束语

本文提出一种适用于多波束卫星系统的US-SSLNR预编码算法，该算法在每个用户上进行SSLNR值得计算，有效降低了各用户码流间的增益差，并充分利用多波束卫星系统信道特点，降低算法复杂度。分析表明，相比SSLNR-THP及PA-SSLNR算法，本文算法通过引入ri，有效降低了运算复杂度。仿真结果表明与SSLNR-THP相比，本文算法及PA-SSLNR算法有效提高了误码性能，在高信噪比区域误码率性能提升大约4.7 dB。